基于极限学习机的焊点质量检测
马立勇,袁统帅
哈尔滨工业大学(威海)信息与电气工程学院,山东 威海 264200
1 引言
电子产品的焊点质量直接影响产品的可靠性,因此,对电子产品焊点质量进行检测,是保证电子产品质量的重要工作。自动化和计算机技术的发展促进了机器视觉代替人工进入工业生产检测环节,从而有效地解决在高速、高精、微距、超视等情况下人类的视觉容易出现疲劳、受环境和主观因素影响大等问题。
由于实际生产工艺的不成熟,受温度、焊锡量及元件贴装位置等因素影响,各焊点的形状与表面千差万别,往往会产生缺陷,比如焊料过少导致的虚焊等,这就给焊点的图像检测带来了诸多的困难。虽然焊点检测技术得到了快速发展,但是在工业生产当中还是以抽样破坏检测的方法进行焊点检测,这种方法不能满足生产中高效率、高检测率的要求。因此,对焊点缺陷进行快速的无损检测具有重要意义。为了解决该问题,出现了基于神经网络的检测方法[1-3],但是这类方法由于特征提取不明显,分类方法粗浅,容易出现误检或者漏检。为了能够更有效地检测焊点质量,将极限学习机(Extreme Learning Machine,ELM)算法应用到分类检测中去,从而准确检测焊点质量。虽然神经网络系统辨识经过了50多年的发展,取得了很多显著的理论成果,但是大规模系统中的大数据量、高维度以及数据的高不确定性,使神经网络的辨识速度很难满足实际的要求。此外,像核算法、人工神经网络、深度学习等方法不仅需要大量的训练时间,并且会出现“过饱和”、“假饱和”等各种问题[4-6]。而通过主成分分析(Principal Component Analysis,PCA)将高维度数据可视化,简化数据以便学习,再利用极限学习机算法训练速度快,泛化能力好的特性,使得极限学习机在焊点检测分类中具有很大的优势。本文对焊点图像进行预处理后,采用极限学习机算法对焊点的特征图像进项检测分类,有更高的检测准确率。
2 相关理论
本文使用的方法主要包括两部分:主成分分析和极限学习机。图像分类时,原始数据往往是高维度的,不利于学习,因此通过主成分分析将用于学习的数据先进行降维处理,更便于后续利用极限学习机进行数据分类。
2.1 主成分分析
主成分分析可以和机器学习相结合进行分类。主成分分析利用降维的思想将高维度数据映射到低维度空间,并期望所投影的维度上方差最大。对于d维度空间的n个样本 z1,z2,…,zn,其矩阵形式为 Zd×n=[z1,z2,…,zn],对所有列取平均,可得:

这里n为样本总数,m为样本均值。令Zˉ=[m,m,…,m],则定义样本集X的协方差矩阵:
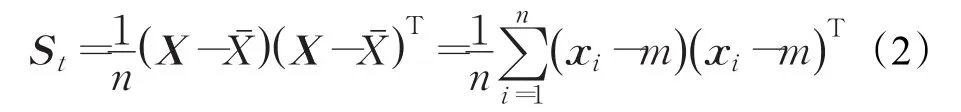
设 St的秩为 k,则 λ1≥λ2≥…≥λk;wi,i=1,2,…,k为对应的特征向量。累计贡献率为:

当ηm大于某个阈值(通常要达到70%~80%)时,可认为主成分数目为m。wi,i=1,2,…,m称为样本主成分,W=[w1,w2,…,wm]为主成分矩阵。
使用主成分分析得到的新变量为:

由此可见,通过主成分分析可以将样本降维,样本从n×d维降低至n×m维,这样就只保留了贡献率较高的部分[7]。
2.2 极限学习机
极限学习机是一种快速训练的单隐层前馈神经网络的学习算法。极限学习机相比于传统的方法,其网络训练速度提高了数千倍,并且不影响网络的收敛能力。
对于N个任意不同的样本(xi,ti),其中 xi=[xi1,xi2,…,xin]T∈Rn,ti∈R ,i∈1, N 。对于具有L个隐层神经元的单隐层前馈神经网络,可记为:

xi=[xi1,xi2,…,xin]T∈Rn表示输入层与隐层第i神经元之间的输入权值,βi表示隐层第i个神经元与输出层神经元之间的输出权值,bi表示隐层第i个神经元的阈值,wi⋅xj表示 wi与 xj的内积。
具有L个隐层神经元的单隐层前馈神经网络采用激励函数g(x),可以逼近来自同一连续系统的N个输入样本,预计输出yi为:

这里ε是噪声,其模型如图1所示。
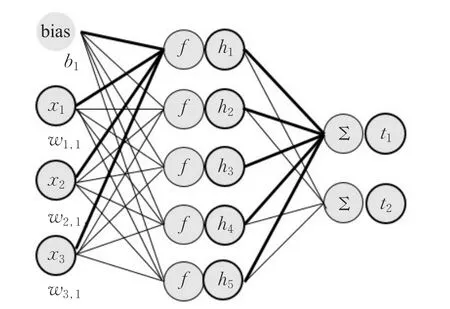
图1 ELM模型
隐层神经元将输入数据转换成不同的表示。转换分为两个步骤进行,首先通过输入层权重和阈值将数据映射到隐层,其次转换映射数据。极限学习机中的非线性转换函数可以很好地提高其学习能力。隐含层数据表达h可以用于查找输出权重。
神经网络中的隐层不局限于一种转换函数,不同的功能可以使用不同的函数(sigmoid、hyperbolic tangent、threshold等)[8-9]。通常情况下,线性网络节点数等于数据特征数。
实际中,极限学习机通过矩阵形式求解,使用矩阵易于编写,并且在计算机上运行速度快,其矩阵形式可以表示为:

虽然极限学习机包括训练方面,但是和其他神经网络一样,网络本身是不可见的,数学上,只有一个矩阵描述两个线性空间的映射关系。因此极限学习机可以视为两个映射:输入XW和输出Hβ,它们之间是一个非线性转换H=g(XW+b),隐含层节点数目决定了W、H和β的大小[10-11]。
拥有不同的隐含层类型则对于每一种类型都是独立的,两种隐含层类型:

线性隐含层可以加入到极限学习机中:
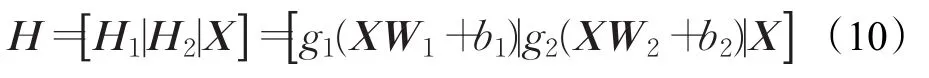
由上述介绍可知:

训练这个网络等同于求解方程(7)的最小二乘解。认为H的秩等于N,在这一假设下,可计算左伪逆为:

则有:

3 实验方法
采用极限学习机算法进行焊点检测可以直接应用于实际生产当中,根据实际生产需要,要求焊点检测准确率在95%以上,实现器件的实时检测。
本文采用极限学习机算法,对所采取到的图像进行处理时,重点包括两方面的工作,一方面是图像预处理提取特征,另一方面是对特征图像检测分类。
3.1 系统构建
如图2所示,视觉检测系统包括条形光源、PC机和相机。相机采用Basler acA 2500-14gm GigE相机配有Aptina MT9P031 CMOS芯片,每秒14帧图像,500万像素分辨率。该相机外观轻巧,适合安装在狭小空间。利用图2所示系统采集焊点图像。

图2 实验系统图
3.2 图像预处理
在所有的待检测焊点图像库中随机获取部分图像,对所获得的全部图像进行预处理。用中值滤波去对全部图像进行滤波,可以消除噪声,避免干扰;由于标准焊点是表面光滑的半椭球体,缺陷焊点则是表面不规则形状,采用分水岭算法对图像进行分割,可获得焊点轮廓和分割区域轮廓;最后将获得的分割轮廓图像统一转化成50×50大小的图像作为提取的特征图像。
本文采用的基于极限学习机的焊点检测方法基本步骤如下:
步骤1对测试件进行图像采集,获取焊点图像。
步骤2对焊点图像进行预处理,首先截取焊点所在区域,再进行中值滤波,最后将滤波结果进行分水岭分割,从而获得特征图像。预处理结果均为50×50的图像,将其转换成1×2 500的行向量,通过主成分分析对此行向量进行降维,降低维度至1×87的行向量,作为极限学习机的输入xi。
步骤3确定极限学习机的隐含层节点数目N,确定输入层的输入权值wi和bi,i=1,2,…,N。激励函数为sigmoid,隐含层节点数目为200。
步骤4计算隐含层输出矩阵H和输出权值β:β=H-1T。
步骤5输入测试集,获取测试结果并分析。
4 结果与分析
4.1 测试结果
随机采集合格焊点150张图像和缺陷焊点100张图像,共计250张图像进行图像预处理,随机选取其中的50个合格焊点和50个缺陷焊点预处理结果作为训练样本,剩余的图像预处理结果作为测试样本。图3是合格焊点和缺陷焊点的样本图以及预处理后的结果。
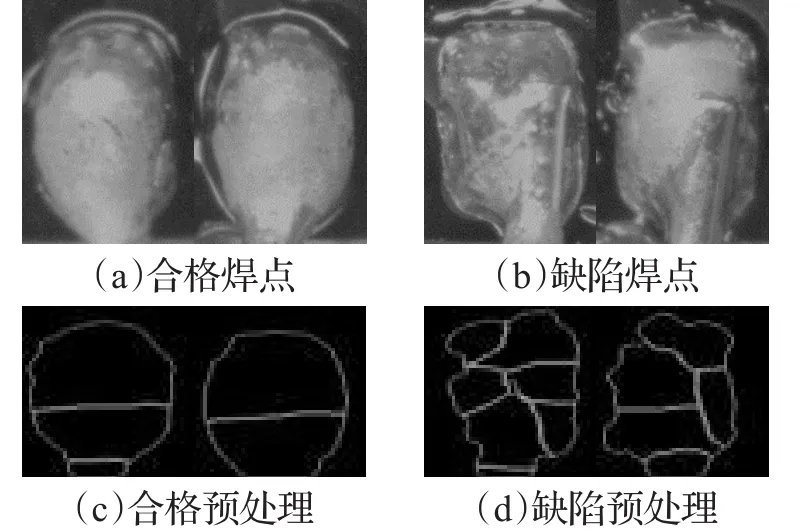
图3 样本图像
对100个合格焊点和50个缺陷焊点进行分类检测,PCA+ELM的计算结果ti(i=1,2,…,150),如图4所示,分类结果如表1。对于缺陷类焊点达到100%的准确检测,避免错误出厂,在合格焊点的检测准确率也达到99%,可以满足检测要求。
4.1.1 准确率对比
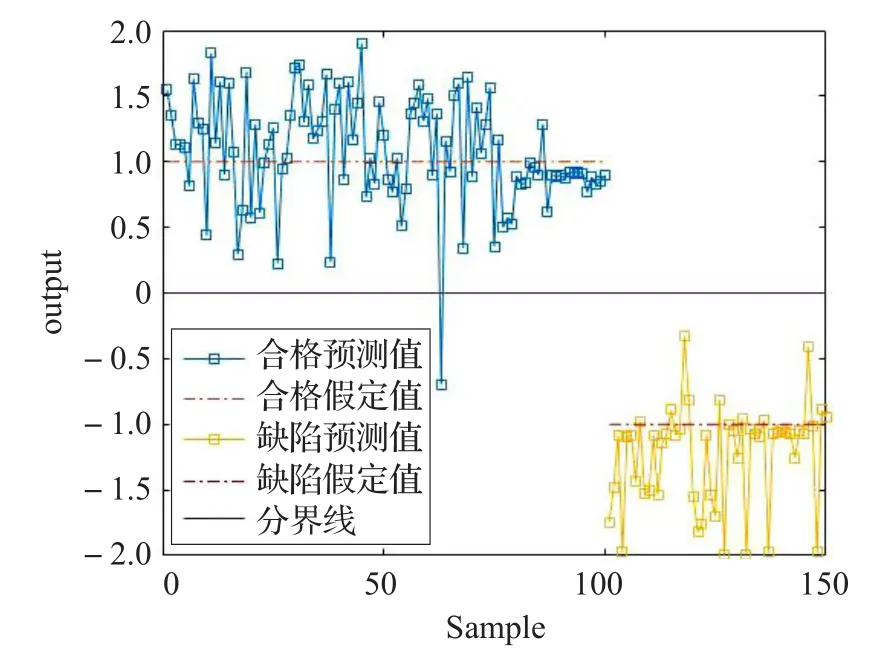
图4PCA+ELM计算结果T

表1PCA+ELM检测结果
传统分类方法有基于核和基于实例算法等。基于核的算法把输入数据映射到一个高阶的向量空间,在这些高阶向量空间里,有些分类或者回归问题能够更容易解决;基于实例的算法常常用来对决策问题建立模型,这样的模型常常先选取一批样本数据,然后根据某些近似性,把新数据与样本数据进行比较。其中比较著名的算法有支持向量机(Support Vector Machine,SVM)和邻近算法(K-Nearest Neighbor,KNN)。最近10年来,深度学习得到了迅速发展,研究工作不断深入,在模式识别和预测估计等领域取得了很大的成功。卷积神经网络(Convolutional Neural Networks,CNNs)是深度学习的一种,已成为图像识别领域的研究热点[12-13]。但是在实现相同成功率的情况下,深度学习算法所需要的样本比极限学习机多很多。
在MATLAB 2015b下,对所提到的各种算法进行测试并比较。仅用ELM进行测试,其准确率没有优势,而PCA+ELM相对于SVM、KNN、CNNs,在拥有相对较高的检测准确率的同时,也具有很大的时间优势,其检测准确率如图5。
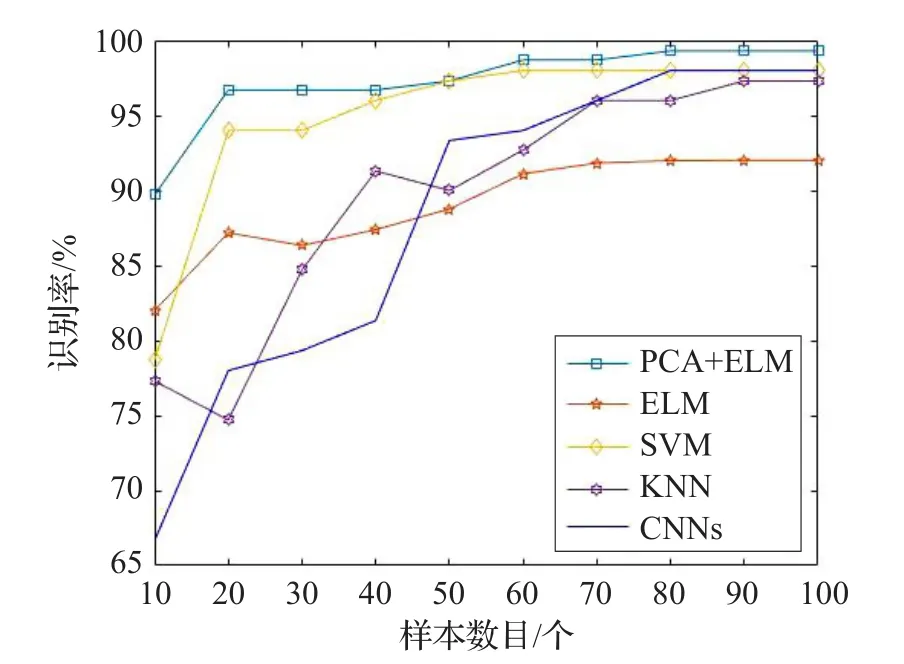
图5 检测准确率对比
为了避免不合格产品的错误出厂,仅靠检测准确率不足以满足性能影响,因此需要新的指标。ROC曲线是描述检测概率和虚警概率的制约关系,用于目标识别算法的评估。通过计算ROC曲线下的面积(Area Under an ROC Curve,AUC)作为判断模型优劣的指标。AUC的取值范围是[0,1],AUC的值越大,说明算法分类性能越好。若AUC为1,表示分类完全正确[14-15]。表2是PCA+ELM和SVM、KNN、CNNs几种算法在不同样本下AUC的值,可以看出,PCA+ELM的分类性能要优于SVM、KNN、CNNs。
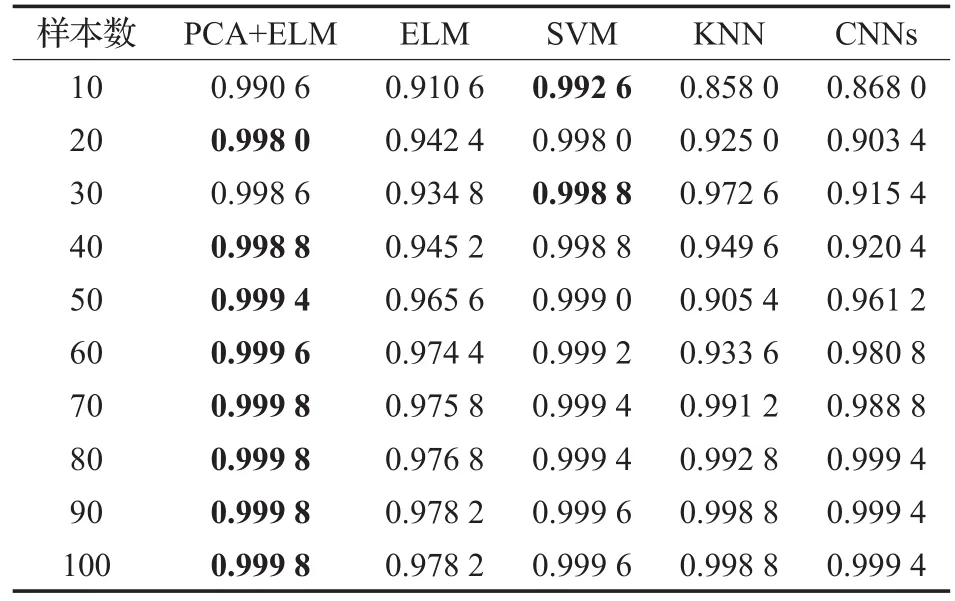
表2AUC比较
从表2数据可以看出,PCA+ELM相对传统分类方法分类性能更好。
4.1.2 时间对比
焊点检测过程中,训练及测试时间是判断算法好坏的一个重要指标,表3是对PCA+ELM、ELM、SVM、KNN和CNNs几种方法的时间统计;图像采集时间和预处理时间相同,分别为2.4 ms和11.0 ms。由表中信息可以看出PCA+ELM明显优于另外4种。
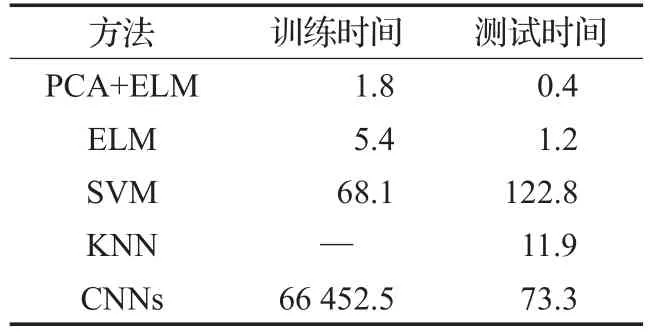
表3 检测时间 ms
CNNs对图像进行训练时,准确率达到98%以上,训练样本迭代次数至少300次,训练时间很长。由表3可见,极限学习机的训练时间远远短于支持向量机、邻近算法和卷积神经网络,在测试时间上也比它们要快。卷积神经网络等算法的检测时间的局限,使其不能实现在线实时焊点检测。
4.2 参数分析
在图像预处理过程中,使用中值滤波进行滤波,可以去除噪声,减少干扰,滤波窗口大小选取影响到检测准确率,因此依次对窗口大小为9×9到41×41的中值滤波进行测试,检测结果如图6。因此在后续检测中,为了使得检测准确率更高,检测结果更稳定,选取窗口大小为31×31的中值滤波。

图6 中值滤波窗口大小测试图
不同情形下可采用不同的隐含层函数,主要的隐含层函数有sigmoid函数、RBF函数和hardlim函数等形式。在实际实验中,隐含层神经元节点数目的选取很大程度决定了整个神经网络的识别精度,也关系到系统的泛化性能。因此对极限学习机的隐含层激励函数和节点数目进行测试,测试结果如图7所示。图中显示sigmoid激励函数测试准确率最高,并在200个神经元之后其检测准确率不再上升,因此在实际检测中选取sigmoid函数,神经元数目选择200个。

图7 隐层参数测试
ELM以其快速的学习能力、良好的泛化性、简单的参数设置等优点,广泛应用于各个领域之中。由上述可得,最终选取大小为31×31的中值滤波窗口滤波后,进行分水岭分割,将处理结果作为训练测试样本,使用极限学习机进行分类,隐含层激励函数为sigmoid,节点数目为200。经过100次测试,得到测试标准差如图8所示,由此可见该算法应用稳定。
使用PCA降维后再用ELM进行焊点分类,大大降低了识别时间,在64位Windows系统下,CPU为i5-4590,MATLAB 2015b中运行,本文算法相对支持向量机、邻近算法、卷积神经网络,检测准确率更高,检测时间缩短,检测性能更好可以实现焊点的实时分类。
综上所述,可见总体指标均达到生产要求。

图8 检测标准差
5 结论
电子产品的焊点质量会影响产品的可靠性,焊点质量检测是保证电子产品质量的重要工作。传统算法检测精度低、耗时长。本文将焊点图像预处理后,采用PCA+ELM对焊点进行分类。基于极限学习机的焊点检测分类是一种适合高速精确测量的检测方法,该方法的整体系统构建简单,占用空间小、精度高。本文方法分类精度高、耗时少,检测准确率和检测时间均达到生产要求,可应用到实际生产中。
[1]Jagannathan S.Automatic inspection of wave soldered joint using neural networks[J].Journal of Manufacturing Systems,1997,16(6):389-398.
[2]Acciani G,Brunetti G,Fornarelli G.Application of neural networks in optical inspection and classification of solder joints in surface mount technology[J].IEEE Transactions on Industrial Informatics,2006,2(3):200-209.
[3]Akusok A,Bjork K M,Miche Y,et al.High-performance extreme learning machines:A complete toolbox for big data applications[J].Access IEEE,2015,3:1011-1025.
[4]Huang Z,Yu Y,Gu J,et al.An efficient method for traffic sign recognition based on extreme learning machine[J].IEEE Transactions on Cybernetics,2016.
[5]Yadav B,Ch S,Mathur S.Discharge forecasting using an Online Sequential Extreme Learning Machine(OS-ELM)model:A case study in Neckar River,Germany[J].Measurement,2016,92:433-445.
[6]Al-Yaseen W L,Othman Z A,Nazri M Z A.Multi-level hybrid support vector machine and extreme learning machine based on modified K-means for intrusion detection system[J].Expert Systems with Applications,2017,67:296-303.
[7]Abdi H,Williams L J.Principal component analysis[J].Wiley Interdisciplinary Reviews Computational Statistics,2010,2(4):433-459.
[8]Huang G B.What are extreme learning machines?Filling the gap between frank Rosenblatt’s dream and John von Neumann’s puzzle[J].Cognitive Computation,2015,7(3):263-278.
[9]Huang G B.An insight into extreme learning machines:Random neurons,random features and kernels[J].Cognitive Computation,2014,6(3):376-390.
[10]Huang G B.Learning capability and storage capacity of two-hidden-layer feedforward networks[J].IEEE Transactions on Neural Networks,2003,14(2):274-281.
[11]Wang Y,Cao F,Yuan Y.A study on effectiveness of extreme learning machine[J].Neurocomputing,2011,74(16):2483-2490.
[12]Hinton G E,Salakhutdinov R R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504.
[13]Makantasis K.Deep supervised learning for hyperspectral data classification through convolutional neural networks[C]//International Geoscience and Remote Sensing Symposium,2015:4959-4962.
[14]董元方,李雄飞,李军,等.基于分辨粒度的gROC曲线分析方法[J].软件学报,2013,24(1):109-120.
[15]杨一,张淑娟,何勇.基于ELM和可见/近红外光谱的鲜枣动态分类检测[J].光谱学与光谱分析,2015(7):1870-1874.

