改进型帝国竞争模型算法的研究
陈 禹,冯 翔,2,虞慧群
1.华东理工大学 信息科学与工程学院,上海 200237
2.上海交通大学 智慧城市协同创新中心,上海 200240
1 引言
1.1 背景与相关工作
帝国竞争算法(ICA)[1]是Atashpaz-Gargari和Lucas于2007年提出的基于帝国主义竞争机制的进化算法,属于社会启发的随机优化搜索方法。目前,ICA已被成功应用于解决实际的优化问题[2-4],比如社会行为的研究,机械设计,电磁学,分类问题等。如控制、数据聚类[5]、工业工程[6]、函数优化、旅行商问题[7-9]、人工神经网络训练[10-11]。ICA最大的问题就是帝国的数量不断减少,这样会导致群体的多样性降低,对于求解最优化问题极为不利。为了克服这一缺点,相关的学者已经提出了许多改进的ICA算法,每个算法都在ICA的基础上有了一定的改进并取得了不错的效果,但是仍有不足。
无论是自然还是社会都有它的存在和进步的法则,人们从社会和自然中汲取灵感和行为思索进行模拟,大致分为三类:第一类是进化算法类似于基因遗传算法,该类算法没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得到较精确的最优解需要较多的训练时间;第二类是基于行为的群算法,例如殖民地优化算法和粒子群算法,该类算法缺乏速度的动态调节,容易陷入局部最优,导致收敛精度低和不易收敛;第三类是建立现象的模拟模型的算法,例如根生长和飓风模型算法,该类算法不够灵活,求得的结果的精度不够。而本文从这三个方面在帝国竞争算法的基础上进行了改进。
在智能算法中存在的一个问题就是个体与群体频繁的交互,这样会导致两种结果,容易陷入局部最优,进而导致其他的个体容易陷入局部最优;这种强交互性的算法要求智能算法一步一步的执行,因此需要很长的运算时间,尤其是问题规模非常大的时候,所以改进的算法要能够保持高效性。
1.2 动机与贡献
本文的动机如下:
早期的ICA改进算法中并未对搜索的精度进行改进,而本文借鉴了以前搜索克服早熟收敛的思想以及帝国相互融合的元素,增强了样本多样性以及帝国之间的交互能力,主要是针对原有的帝国竞争算法(ICA)进行模型上的改进,通过基准函数的测试来检验改进算法的有效性和准确性。
本文的主要贡献如下:
(1)本文建立了改进算法的数学模型来展示算法的进程的优越性。
(2)对新的思想进行了数学建模,制作模型图,并利用代码实现并且做了大量的实验,对算法的有效性和优越性进行了分析。
(3)提供了原算法中缺少的理论证明,为以后的研究提供了一定的理论基础。
2 改进的帝国竞争模型
小世界理论[12-14]描述的是你和任何一个陌生人之间所间隔的人不会超过6个。以此为基础可以联系到每个帝国的殖民地都可以计算出一个参数,然后通过这个参数进行殖民地的同化,保持在一个帝国的国家不只与该帝国相互联系,还能够与其他帝国保持交互,加强全球化的进程,增强在整个帝国网络中的相互关联。
具体定义如下:
在一个帝国中设置总共4个角色,分为帝国、管理者、普通殖民地和叛逃者,具体功能如下:
定义1(统治者)随机区域中cost最小的国家。
定义2(管理者)和统治者距离最近的那个国家设置为整个帝国的管理者。
定义3(普通殖民地)特征不明显的国家。
定义4(叛逃者)距离统治者最远的国家。
(这里的距离都用欧氏距离来表示)
同化过程是先由管理者向着帝国主义国家移动,然后普通殖民地再向管理者移动。
叛逃者是一个帝国中忠诚度最低的一个殖民地。
该算法模拟了帝国在竞争过程中一些行为,具体行为模型如下:
行为模式1:管理者向统治者移动,由于二者距离比较近,所以移动的不是特别明显。
行为模式2:殖民地向管理者移动。
前两种模式的综合图,如图1。

图1 殖民地移动
行为模型3:叛逃者向统治者移动。
为了增强普通殖民地在移动过程中的目的性,引入了忠诚度的概念。
定义5忠诚度是指每个普通殖民地对他所属帝国的忠诚的程度,忠诚度越大则表示该国家距离统治者的距离越近,反之则越远。考虑到如果一个帝国中的殖民地也应该相互的存在竞争否则一个国家无法健康地发展下去,有竞争力的殖民地才能在竞争环境中存在,否则就要被淘汰。
在该模型中,同时应用了竞争和同化的两个概念,每个普通殖民地在计算忠诚度时同国家的管理者竞争,而殖民地都会和其他帝国的统治者进行比较,然后使本帝国的殖民地同化,忠诚度越小的殖民地下次迭代中移动的距离也就越远,如图2所示。
2.1 改进的子模型1:基于忠诚度信息熵的纳什均衡模型

图2 同化与竞争的结合模型图
通常在每个同化过程中,一个帝国总会有背离其统治的国家,在帝国成立的初期,每个帝国的统治一定是混乱的。上文中提到的叛逃者,就是一个帝国中最混乱的国家。所以在竞争机制中设立了两种模式:当满足竞争入口系数的要求时,则按照原算法进行竞争的行为;当不满足竞争的要求时,就利用该模型进行竞争与博弈的行为[16],具体解释如下。
在竞争机制中,每次迭代时一旦发生了竞争和占领的行为都是最弱帝国中的最弱的国家(叛逃者)被其他的强帝国占领,如果不发生占领的行为则在原先基础上进行博弈。在此忠诚度则表示它不离开这个帝国统治的概率。所以忠诚度越低,它的混乱度(信息熵)也就越高。
每个叛逃者的忠诚度信息熵计算如公式(1):
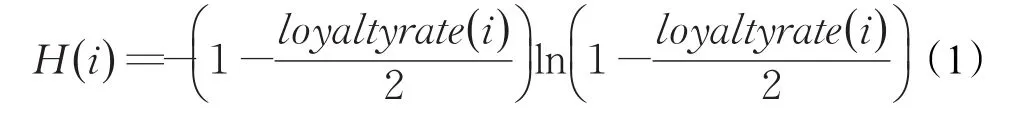
每次博弈叛逃者都有两种策略:
(1)向着本国统治者移动。
(2)成为其他国家的叛逃者,而其他国家的叛逃者必须别的选择合适的帝国成为其叛逃者。
这两种策略二选其一,目的是要达到所有帝国的叛逃者在选择策略之后,使得所有帝国的叛逃者的忠诚度信息熵(H)最小,如公式(2):

在选择局部最优策略的组合时利用纳什均衡的理论进行选择。
2.2 改进的子模型2:基于差异因子的同化模型
这个改进的模型目的是要模拟网络关系中的结点之间的关联。这个模型是为了改善算法搜索范围的广度来避免算法陷入局部最优解。因为一个好的帝国竞争算法不能只通过增加国家的数量来增加搜索范围,应该尽可能地在少量的群体中找到最优解。
在改进的子模型1中,每个普通的殖民地和管理者的连线与管理者和帝国的连线都有一个夹角,在二维群体或者三维群体中,这个夹角表示一个几何空间上的夹角,其实对于多维函数(30)来说,这个角度的取值代表多个国家与统治者的连线向量和统治者与管理者向量的线性相关度,如果角度过小表示相关度比较大,如果过大也表示相关度过大(因为如果是180°的话说明是负相关),所以设计思路便是令相关度比较大的数据变的更具有随机性,这一思想与协同过滤算法计算相似度的公式基本思想保持一致。所以利用公式(3)来计算差异因子:

上述的α和γ是事先设定好的阈值。该函数的图像大致的曲线走势,如图3,具体的α和γ的值会在后面实验中提到。

图3 μj(coli)函数示意图
3 改进的帝国竞争模型算法
设置一个排序矩阵OrderMatrix,把帝国的殖民地的位置存放进来,并且增加两列,一列用于存放该行殖民地的忠诚度,另一列存放计算出来的忠诚率。
忠诚度计算出来以后把矩阵按照忠诚度进行降序排序,排在第一名的作为管理者,最后一名作为叛逃者;忠诚度的计算如公式(4):

得出结果后保存到计算维度增加的第一列。这列引入了所有帝国的位置作为函数的入口,用来计算每个殖民地的忠诚率。
忠诚率的计算公式如公式(5):

得出结果后保存到计算维度增加的第二列。
colonyi(t +1)是新一次的迭代位置,β是忠诚率的矫正系数,μ是下文中计算所得差异因子。
在殖民地的移动过程中,最先移动的是管理者,并且修改了同化系数,这样一个管理者看起来就更像一个帝国的位置,更加区分了管理者与其他殖民地的地位差别。
然后是普通殖民地的移动,殖民地越多,他们的忠诚率也就越小,因为一个帝国中的普通殖民地的忠诚率的和等于1。所以在把忠诚率引入作为参数的时候给每个忠诚率前面乘以了一个普通殖民地的个数,这样既可以让每个殖民地看起来都有不同,又可以保证他们的移动是正确而且多样性的。
同化机制算法模型:
输入:一个帝国中殖民地的位置
输出:迭代后殖民地新的位置
(1)把殖民地位置存储到OrderMatrix矩阵中。
(2)把OrderMatrix增加两列。
(3)按照公式(4)计算忠诚度,并存储到新增加的两列中的第一列。
(4)按照忠诚度从大到小重新排序这些殖民地。
定义第一位为管理者,最后一位为叛逃者,其余的为普通殖民地。
(5)管理者设定参数向着统治者移动,而普通殖民地则是向管理者移动。
(6)利用公式(5)把忠诚度归一化存储到第二列中。
(7)输出新的殖民地位置矩阵。
3.1 改进的子模型1:基于忠诚度信息熵的纳什均衡模型
该模型算法的目的就是利用最大最小公平性来寻找局部最优的纳什均衡策略组合。
基于忠诚度信息熵的纳什均衡模型算法流程:
输入:所有帝国中统治者的位置及其叛逃者的位置
输出:所有帝国中统治者的位置及更新后的叛逃者的归属情况和移动位置
(1)计算所有剩余叛逃者的忠诚度信息熵。
(2)选择信息熵最大的叛逃者进行步骤(3),(4)两种策略选择。
(3)叛逃者向帝国统治者移动并计算移动后的忠诚度信息熵。
(4)假定该叛逃者属于其他的帝国,计算它在其他忠诚度信息熵,并选取出最小的一个。
(5)比较步骤(3)和(4)的大小,选取小的进行决策:若第(3)步的策略小,到第(5)步;若第(4)步的策略小,到第(6)步。
(6)保存叛逃者的新位置,并移除此帝国,其余帝国成为新的输入。
(7)交换两个帝国中叛逃者的位置,并移除步骤(2)中叛逃者所属帝国,其余帝国作为新的输入。
(8)新的输入帝国数目若大于1则返回步骤(1);否则结束该模型算法。
3.2 改进的子模型2:基于差异因子的同化模型
在算法中定义了一个差异因子μ来表示每个向量的差异度,令求得的角度为θ,计算公式如下:
当θ<60°,μ=0。
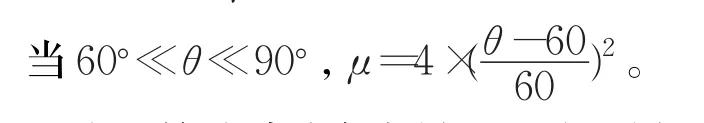
上述函数是随着自变量的取值的增大而单调递增的,但是对于角度函数来说,应该是关于90°对称的,举个例子来说80°的差异因子应该和100°的差异因子是一样的,当θ的取值为90°时得到的差异因子应该是最大的这里设为1。所以上述公式前面变成了乘4。所以有以下公式:
当,(对称性)。
当θ>120°,μ=0。
上述公式中差异因子大,表示数据的搜索范围越广,差异因子越小则认为的更改它的值来实现样本多样性。
综上得到公式(7):
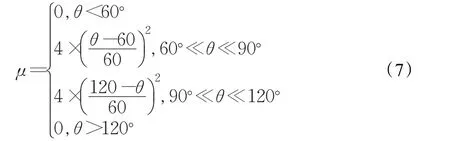
上述分段函数的图像如图4。

图4 分段函数图像
算法描述:
增加排序矩阵OrderMatrix的一列用来存放普通殖民地的差异量。
按照上述公式把差异因子归一化。
求得计算管理者与统治者的向量和普通殖民地与管理者之间的向量。
令 μ=arccos θ,求得θ代入到公式(6)中。
计算下一次的迭代位置。
子模型2算法流程:基于差异因子的同化模型。
(1)把新位置存储到OrderMatrix矩阵中。
(2)把OrderMatrix再增加一列。
(3)计算管理者与统治者的向量和普通殖民地与管理者之间的向量。
(4)求两个向量的夹角,并利用公式(7)规范化。
(5)μ=tan(arccos θ),求得 μ代入到公式(6)中。
4 改进的帝国竞争模型理论分析
4.1 算法收敛性证明
定理设A为n阶方阵,则的充要条件为ρ(A)<1。该定理证明略。
定理 对任意初始向量x(0)和右端项g,由迭代式x(k+1)=Mx*+g产生的向量序列{x(k)}收敛的充要条件是 ρ(M )<1,证明略。
在改进的帝国竞争算法中的同化模型的同化公式如下:
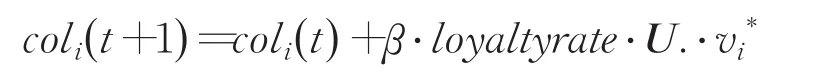
由于a1,a2,…,a29,a30是相互独立的,则
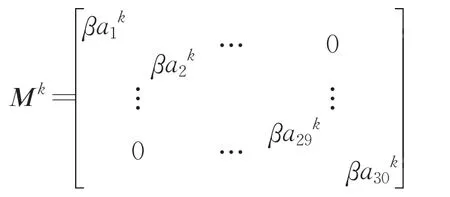
令a=0.99,则由2×ak<1,得K>68时,可以满足公式(8):
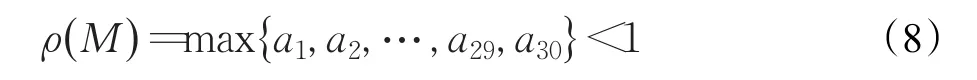
令a=0.99,则由3×ak<1,得 K>111时,可以满足公式(8):
令a=0.99,则由4×ak<1,得 K>137时,可以满足公式(8):
这三个公式的不同在于a前面的系数也就是趋紧系数β不同,下面会对这个系数做一些实验。

上述公式中,对于:

满足,则该向量收敛于imp。
4.2 利用最大最小公平性求最优策略
为简单求证,假设还剩下两个帝国,每个帝国有一个叛逃者,则剩余的策略有两种组合:一是两个叛逃者分别向各自统治者移动,另外一个策略就是他们两个交换位置,这时候只需要计算两者的忠诚度信息熵的和取最小作值的策略组合为最优策略:

假如还剩三个帝国,则总共有23-1=4种策略可供选择,按照前文提出的算法步骤,先选择一个信息熵最高帝国:

这个被选择的帝国中的叛逃者有三种策略选择,一是向着自己帝国的统治者移动,其余两种和其他两个帝国的统治者交换位置,分别记信息熵的变化量为∆move,
若则该叛逃者向着他的统治者移动,其他两个帝国的叛逃者按照还剩两个帝国的时候进行决策,这时候的信息熵变成:
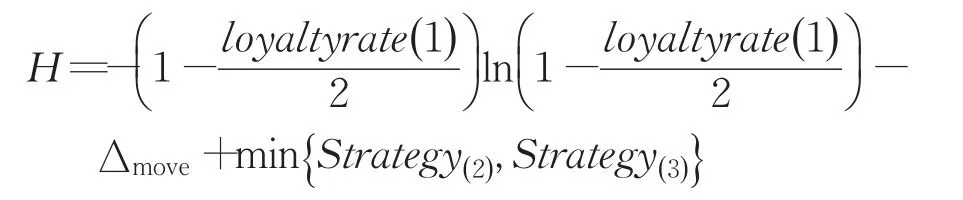
根据上式,显而易见,任何其他的策略得到的H′均小于H。
若存在∆exchange_i>∆move,则选择∆exchange_i中最大的一个,假设是,那么他和该帝国中的叛逃者交换之后得到的忠诚度信息熵为:
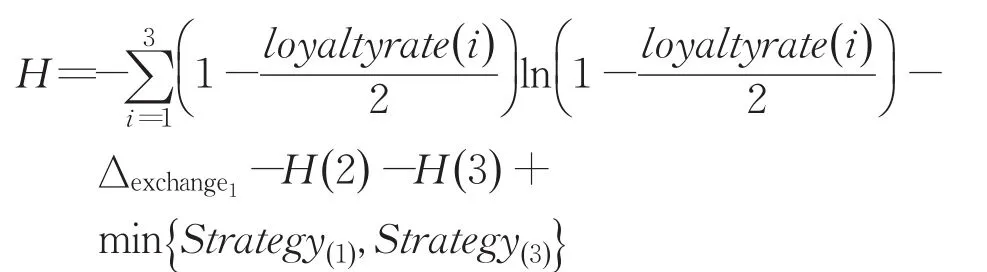
根据上式,显而易见,任何其他策略得到的H′均小于H。
5 改进的帝国竞争模型的实验
改进算法可以比原ICA文章中提到的测试函数更快得到最优值。
5.1 比较实验
实验主要运用14个函数进行比较,如表1。ICA参数设置,如表2所示。得到的最优值比较如表3(DICA),数据来源于参考文献[4,15]。随后反复多次实验,得到算法的平均值和标准差,如表4。
从表3和表4中以及实验结果可以看出,该算法对于多模函数(很多极值点)的搜索做得不错,也就是说对于算法的搜索范围有了很大的提高,因为别的算法要通过增加国家的总个数来增加搜索广度,而且根据每个算法的收敛函数图像来看,大多的收敛都是在1 000次左右,说明算法的稳定性有了很大的提高。对于单模函数来讲,效果稍有提升但是不是特别明显,为接下来的研究工作指明了方向。
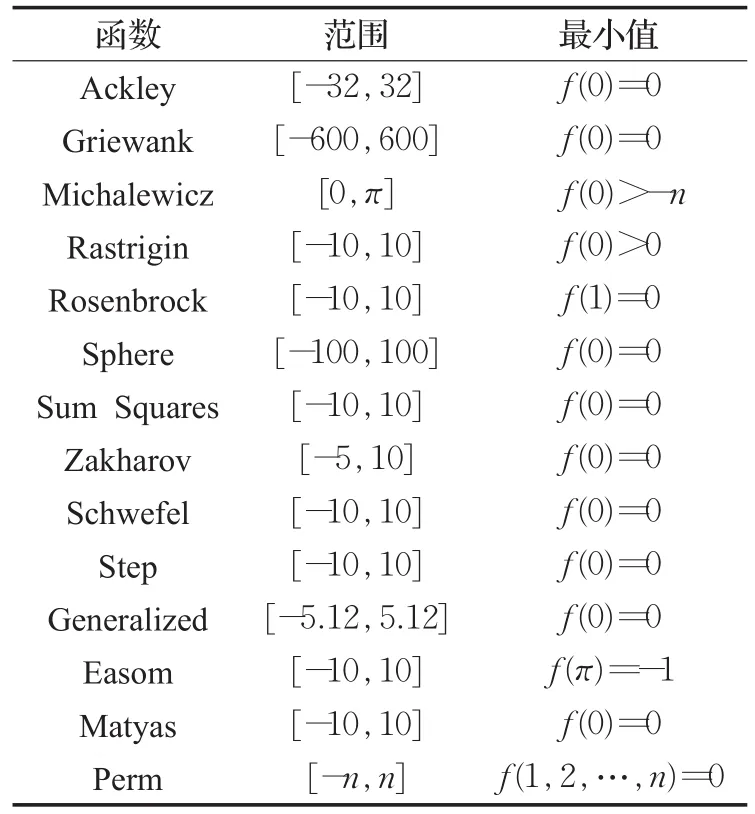
表1 函数范围及最小值
5.2 差异因子参数设置实验
在计算差异因子的模型中,每个殖民地都可以和管理者与统治者三点形成一个夹角,利用Michalewicz函数反复试验得到6组随机数据。
在数据中显示每一列表示一个帝国中的普通殖民地与管理者和统治者三点之间的夹角。从数据中可以看出,求得的角度都是在60°~120°之内,如图5所示,所以把这两个作为模型2的两个参数。
这样设置参数有两个目的:一是纠正不正常的数据,二是让正常的数据更加随机化来增加样本多样性。

图5 殖民地夹角示意图
在算法中,定义了一个差异因子μ来表示每个向量的差异度,令求得的角度为θ,计算公式如式(7)。
5.3 竞争入口系数设置实验
主要研究了帝国减少(融合吞并)时的时间融合点。帝国融合成为一个统一体以后整个帝国的竞争力的值(cost)就不会再发生变化了。因为在全局最优解的搜索过程中,主要有两个因素影响最终的结果,一个是前面迭代时候对全局搜索范围的覆盖广度,一个是后面迭代时候对精度的搜索。对于一个好的极值搜索迭代算法,应该在最初的时候能够遍历所有的搜索的范围,但是如果唐突地去增加国家的个数会增加系统运行的负担,所以在迭代的时候选择让算法自主地去选择一个时间节点去分开广度搜索和精度的搜索是一个不错的想法,而帝国融合的过程时间是决定这个时间节点的关键因素所以对竞争吞并的迭代做了测试,如表5所示。
实验分析(算法稳定性):
(1)从表5中得到一个结论,最后一次的吞并发生的越晚,得到的全局最优值大致越小。但是这个算法的稳定性还不足,因为最后一次的融合的迭代时间10组数值的标准差是除了加粗字体中数值中相对较大的,所以选择合理的控制算法的收敛时间来达到最优值的求解。

表2 参数设置
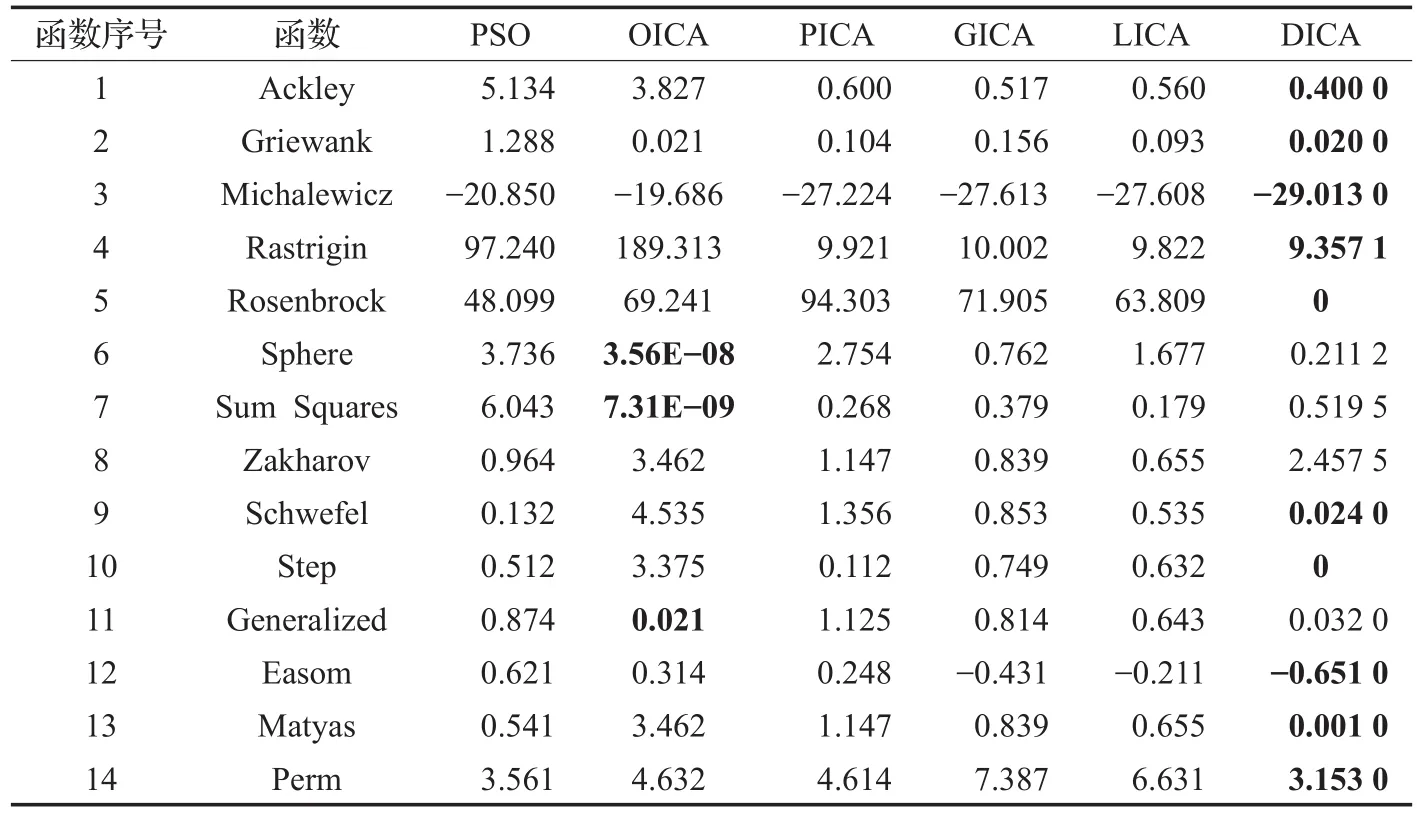
表3 函数最优值比较

表4 平均值和标准差比较
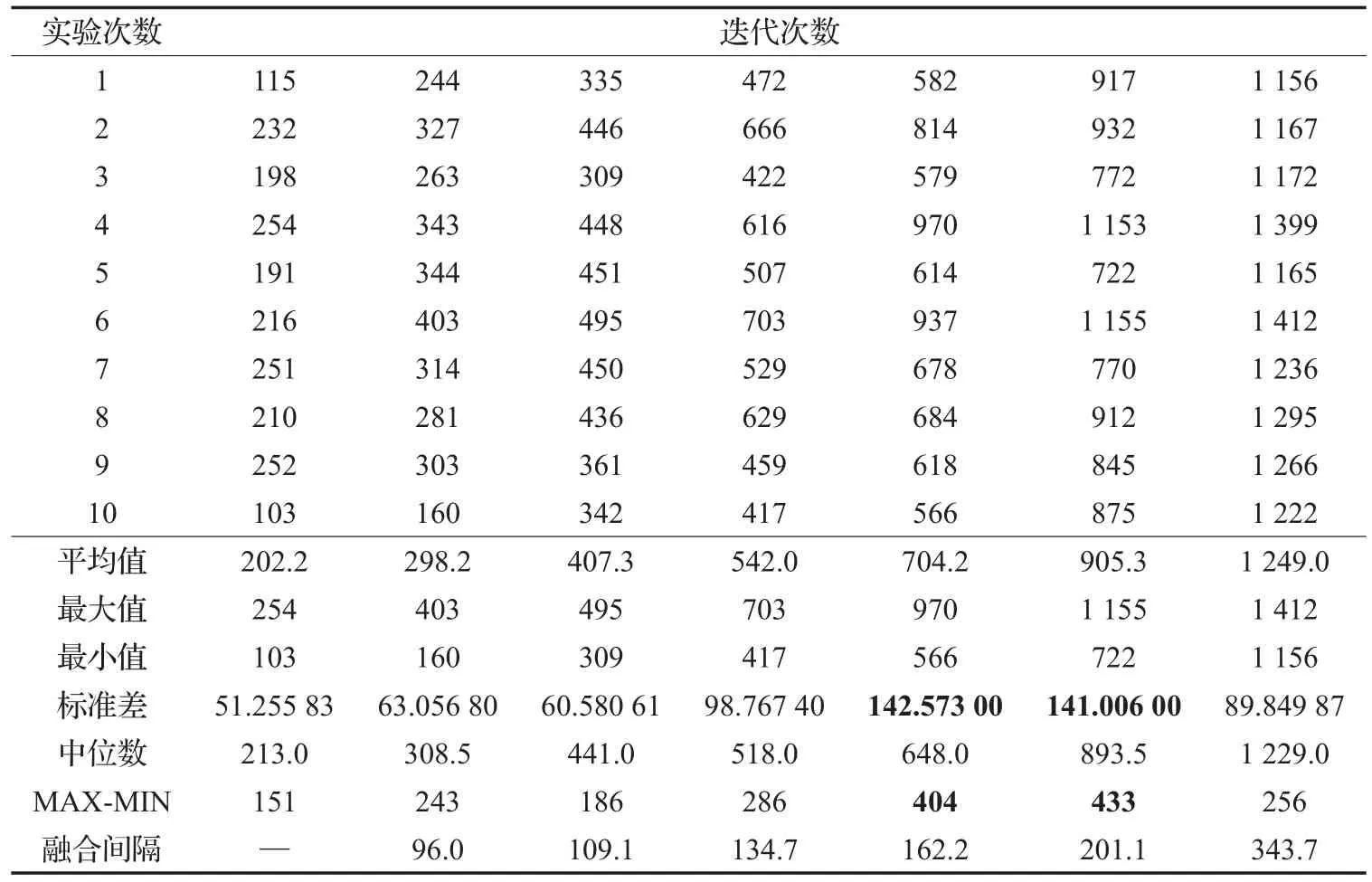
表5 帝国融合时间节点
(2)在表5中加粗的数据是标准差最大的两组数据,并且它们的标准差和最大值减去最小值的值也比较相近,说明算法在这个阶段是最不稳定的,所以在同化过程中控制这一个迭代时间段加速算法的收敛和放宽帝国融合的条件,而最后一次融合之前又严格了同化的条件。
(3)在实验分析(2)中减缓了最后一次融合的时间是为了能够找到更加好的最优值,所以又计算了融合间隔数据来确定时间点:从上述数据来看,随着迭代次数增加,融合的间隔也就越长,最后选择倒数第二个和倒数第三个数据作为动态的融合时间节点,也就是平均值的前50到后50的迭代范围(650~950)来加速融合速度,也就是总迭代进度的在这个时间段内,把吞并融合的概率系数增加到0.15(原算法是0.11),在这个时间段以后又把帝国融合的概率系数减小到0.05。
如图6,虽然到了第1 500次的时候帝国总数还没有达到1个,但是全局最优解的结果已经要好过之前静态的0.11。

图6 融合概率系数为0.11的收敛图像
6 总结与展望
本文主要研究了帝国竞争算法的优化算法以及对优化算法的实验验证,主要包括:(1)利用忠诚度信息熵来增进殖民地与其他国家的联系;(2)引入了差异因子来增加搜索的多样性;(3)设置迭代的动态时间节点控制收敛过程的参数来弥补不同阶段迭代的缺陷;(4)补充了原ICA算法中没有的理论证明;(5)进行了有效性实验和比较实验来验证改进算法的可行性。
该算法属于社会启发的随机优化搜索方法,目前这种算法已经被应用于多个领域,如社会行为的研究及机械设计等,希望这类算法能够应用到更多的领域,解决更多的相关问题。
[1]Atashpaz-Gargari E,Lucas C.Imperialist competitive algorithm:An algorithm for optimization inspired by imperialistic competition[C]//Proceedings of IEEE Congress on Evolutionary Computation,Singapore,2007:4661-4667.
[2]Forouharfard S,Zandieh M.An imperialist competitive algorithm to schedule of receiving and shipping trucks in cross-docking systems[J].The International Journal of Advanced Manufacturing Technology,2010,51(9/12):1179-1193.
[3]Bahrami H,Faez K,Abdechiri M.Imperialist competitive algorithm using chaos theory for optimization(CICA)[C]//Proceedings of the 2010 12th International Conference on Computer Modelling and Simulation(UKSim’10),Cambridge,UK,2010.Wanshington,DC,USA:IEEE Computer Society,2010:98-103.
[4]郭婉青,叶东毅.帝国竞争算法的进化优化[J].计算机科学与探索,2014,8(4):473-482.
[5]Niknam T,Fard E T,Ehrampoosh S,et al.A new hybrid imperialist competitive algorithm on data clustering[J].Sadhana,2011,36(3):293-315.
[6]Nasab E H,Khezri M,Khodamoradi M S,et al.An application of imperialist competitive algorithm to simulation of energy demand based on economic indicators:Evidence from iran[J].European Journal of Scientific Research,2010,43:495-506.
[7]Feng Xiang,Francis C M L,Gao Daqi.A new bio-inspired approach to the traveling salesman problem[J].Information Sciences,2013,233(6):87-108.
[8]Yannis M,Magdalene M,Georgios D.Honey bees mating optimization algorithm for the Euclidean traveling salesman problem[J].Information Sciences,2011,181(10):4684-4698.
[9]Dorigo M,Gambardella L M.Ant colonies for the travelling salesman problem[J].BioSystems,1997,43(2):73-81.
[10]Taghavifar H,Mardani A,Taghavifar L.A hybridized artificial neural network and imperialist competitive algorithm optimization approach for prediction of soil compaction in soil bin facility[J].Measurement,2013,46(8):2288-2299.
[11]高海兵,高亮,周驰,等.基于粒子群优化的神经网络训练算法研究[J].电子学报,2004,32(9):1572-1574.
[12]Behnamian J,Zandieh M.A discrete colonial competitive algorithm for hybrid flow shop scheduling to minimize earliness and quadratic tardiness penalties[J].Expert Systems with Application,2011,38:14490-14498.
[13]Iamnitchi A,Ripeanu M,Santos-Neto E,et al.The small world of file sharing[J].IEEE Transactions on Parallel and Distributed Systems,2011,22(7):1120-1134.
[14]Inaltekin H,Chiang M,Poor H V.Average message delivery time for small-world networks in the continuum limit[J].IEEE Transactions on Information Theory,2010,56(9):4447-4470.
[15]Bahrami H,Faez K,Abdechiri M.Imperialist competitive algorithm using chaos theory for optimization(CICA)[C]//Proceedings of the 2010 12th International Conference on Computer Modelling and Simulation(UKSim).Cambridge,UK:IEEE Computer Society Conference Publishing Service,2010:98-103.
[16]魏蛟龙.基于博弈论的网络资源分配方法研究[D].武汉:华中科技大学,2004.

