裂缝性致密油藏体积压裂水平井压力动态分析

武治岐，王厚坤，王睿

（中国石油 新疆油田分公司 a.重油开发公司；b.工程技术研究院；c.采油一厂，新疆 克拉玛依 834000）

中国致密油资源分布广，在鄂尔多斯、准噶尔、柴达木、四川、渤海湾、松辽等盆地都有发现，是后续能源接替的重要组成部分。体积压裂技术的发展使得致密油气资源开发成为可能，密集的压裂改造，使得多组剪切裂缝、诱导裂缝相互交错，减小了渗流阻力，从而实现致密油藏的高效开发[1-2]。近年来，很多学者针对致密油藏体积压裂水平井做了大量研究，解析和半解析模型方面，一般将井控范围划分为多个渗流区域耦合求解，主要包括三区复合模型 、四区复合模型[7]和五区复合模型[8]，这些模型都假设各个区域内渗流遵循线性流，不能准确反映实际储集层渗流特征。数值模型运用数值差分方法，对致密储集层水平井多段压裂产能影响因素的敏感性进行了分析[9-11]，文献［12］则是基于有限元方法建立了致密油藏水平井多段压裂不稳定渗流模型。数值模型虽然能很好地表征压力动态特征，但计算精度受网格划分及时间步长影响，计算过程相比解析和半解析模型复杂。本文基于格林函数、镜像反演及压力叠加原理，建立了箱式封闭边界裂缝性致密油藏体积压裂水平井压力动态分析半解析模型，能够简明反映致密油藏水平井及储集层属性参数对压力动态传播的影响，方便添加井筒存储系数及表皮因子，可以利用试井及生产数据，得到致密油藏体积压裂水平井裂缝及储集层相关参数。

1 模型建立

1.1 物理模型

对致密储集层水平井实施较为密集的多段水力压裂改造，在形成多条人工主裂缝的同时，裂缝间脆性基质受到拉伸或挤压，产生数量较多的错位剪切裂缝。剪性裂缝、张性裂缝和自然微裂缝相互交织，在主裂缝及水平井井筒附近形成一定区域的改造体积，构成一个由基质与裂缝网络组成的复杂渗流系统（图1）。整个系统流体渗流都是在压力差驱使下进行的，流体渗流顺序为基质→改造裂缝网络→人工主裂缝→水平井筒。由于储集层致密，渗透率极低，相比裂缝的导流能力，基质流体渗流能力相对较弱。以准噶尔盆地吉木萨尔凹陷A井为例，基质平均渗透率0.012 mD，人工裂缝半长150 m左右，基质导流系数远小于人工裂缝导流系数（0.010～0.150 mD·cm），因此，人工主裂缝定性为无限导流裂缝[13-16]，流体在裂缝中渗流遵循达西定律。对于由基质及交错裂缝构建的体积改造区域，假设整个区域压裂改造均匀，并使用Warren-Root模型来表征体积改造区域内基质—裂缝间渗流关系及裂缝系统空间展布。水平井体积改造以外区域受到体积压裂改造影响极弱，没有形成有效的渗流通道，对水平井生产贡献极少[13-16]，可忽略不计。

综上所述，模型基本假设包括：①致密油储集层上、下边界封闭，各向同性，厚度均一，岩石微可压缩；②只考虑单相渗流，符合层流特征，流体微可压缩；③主裂缝与水平井井筒垂直，等臂压裂，无限导流；④体积改造区域内改造裂缝均匀分布，外边界箱式封闭；⑤等温生产，流体在裂缝中渗流规律符合达西定律。

1.2 数学模型

建立如图1所示三维正交坐标系，已知箱式封闭区域中心处有一口多段压裂水平井，所有裂缝均为纵向穿透、等臂压裂横切裂缝，裂缝属性一致，且都与水平井井筒垂直，水平井定产生产，井筒除压裂段外不射孔。

图1 致密油藏体积压裂水平井示意图

1.2.1 箱式封闭双重介质油藏点源解

根据质量守恒以及达西定律，考虑岩石及流体微可压缩，裂缝中各个方向的渗透率相同，裂缝系统控制方程可以表述为[17]

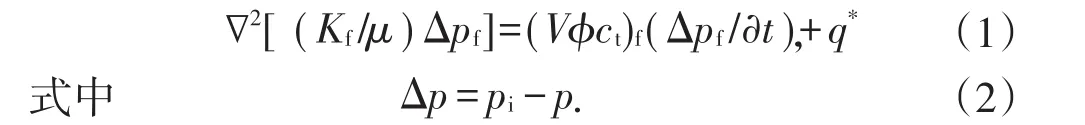
忽略基质内流体渗流，基质提供给裂缝系统的体积流量可以表示为

基质到裂缝系统的体积流量与系统压力差成正比，那么体积流量同时满足方程：

无量纲变量定义为

将（3）式代入（1）式，（4）式代入（3）式，同时无量纲化后，可以得到：

定产生产时，内边界条件为

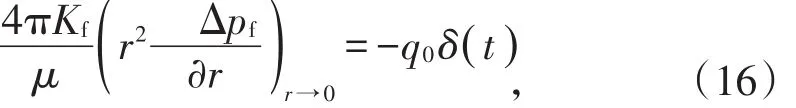
式中

外边界条件为

初始条件为

结合（14）式和（15）式，Laplace变换后有：

式中

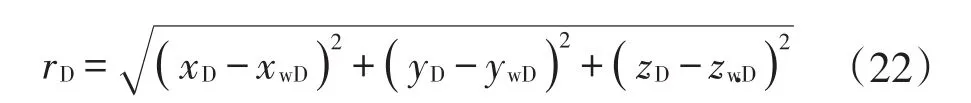
将初始条件及边界条件代入（20）式，联合求解可以得到双重介质油藏无限大地层Laplace空间下点源解，其表达式为

如图1所示，z=0以及z=hD处分别为上、下封闭边界，储集层厚度均匀，根据（23）式，进行镜像反演和压力叠加，可以得到考虑上、下封闭边界无限大双重介质油藏Laplace空间下点源解，其表达式为

为求得箱式封闭双重介质油藏Laplace空间点源 解，对（24）式进行x和y方向镜像反演及压力叠加：

1.2.2 箱式封闭油藏体积压裂水平井压力解

（25）式对zwD从0到hD进行积分，再对xwD从xwD-1到xwD+1进行积分，得到一条完全穿透地层横裂缝的压力

解：

式中

假设体积压裂水平井共产生了N条主裂缝，考虑N条主裂缝同时生产，储集层中任意位置处产生的无量纲压降等于每条裂缝独自生产时产生的无量纲压降的代数和，根据Duhamel褶积有：

对（37）式进行Laplace变换后有：

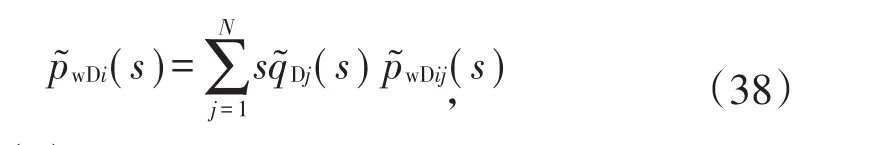
式中 p͂wDij(s)= Δp͂(xwDi,ywDi,zwDi,xwDj,ywDj,zwD.j, s )（39）

所有裂缝流量的总和等于水平井产量：

不考虑井筒摩阻，裂缝为无限导流，则裂缝各处井底流压相等，水平井定产生产，根据（38）式，对于每一条裂缝都有一个方程，结合（40）式，构建成（N+1）个方程组成的线性方程组：

对（41）式进行求解，可以同时得到任意时间下，每一条裂缝对应的瞬时体积流量及水平井井底压力。如需考虑井筒存储系数及表皮因子的影响，对La⁃place空间下井底压力计算公式（38）式进行修正：

用（41）式求Laplace空间下井底压力，不考虑井筒存储系数及表皮因子的影响，运用Stehfest数值反演[18]可以求得体积压裂水平井双对数井底压力传播曲线（图2）。图2是无量纲箱式封闭边界，x方向无量纲边长为5 000，y方向无量纲边长为5 000，无量纲裂缝半长为1，无量纲裂缝间距为0.65，裂缝数为7条，储容比为0.01，窜流因子为10时的无量纲井底压力及压力导数曲线，从图2可以看出，井底压力响应过程可划分为6个渗流阶段：①人工裂缝线性流（第一线性流）阶段，无量纲井底压力及压力导数曲线相互平行，双对数曲线表现为井底压力及压力导数曲线斜率都为1.0；②双重介质（基质—裂缝）窜流阶段，表现为井底压力导数曲线下凹，这个过程中同时发生在裂缝系统和主裂缝中的双线性流特征被掩盖，这是由于裂缝导流能力远大于基质渗流，因此在裂缝系统出现流动现象的同时，窜流便随之发生；③第一径向流阶段，随着井底压力降低，裂缝附近区域内流体径向汇入人工主裂缝，在双对数坐标图上，井底压力导数曲线趋于水平；④第二线性流阶段，随着井底压力受效范围向外波及，离水平井井筒及裂缝较远区域，流体垂直于水平井井筒方向流入生产井，在双对数曲线上表现为井底压力导数倾斜；⑤拟径向流（第二径向流）阶段，随着井底压力传播范围扩大，外围流体呈椭圆形前缘推进汇入生产井，双对数曲线上井底压力导数趋于水平，斜率为0.5；⑥封闭边界流阶段，井底压力传播到达封闭边界，无量纲井底压力及压力导数曲线开始重合，呈45°上扬。

图2 体积压裂水平井双对数井底压力传播曲线

2 实例分析

以准噶尔盆地吉木萨尔凹陷A井为例，该井目的层二叠系芦草沟组为咸化湖沉积，储集层横向连续发育，平均孔隙度为10.99%，平均渗透率为0.012 mD，测试的44块样品中，渗透率小于0.100 mD的样品占90%以上，为典型低孔致密储集层。地面原油密度为0.89 g/cm3，50 ℃下平均原油黏度为73.45 mPa·s，平均凝固点为24.84℃，属于中质、较高凝固点的高含蜡原油。A井完钻井深4 366 m，水平井段长1 233 m，完井后实施体积压裂改造，根据设计，压裂井段长度1 140 m，共压裂15段。压裂后，15条裂缝中有13条能分辨主走向，每条裂缝向各个方向都有延伸，主裂缝半长为110～230 m，平均裂缝半长为148 m，裂缝间距为45～134 m，平均裂缝间距为81 m.系统试井前，使用4 mm油嘴生产，日产液量34.5 m3，日产油量22.8 m3，含水率34%.系统试井设计，先关井测复压759 h，记录压力恢复试井测试数据，然后开井使用5 mm油嘴生产120 h，记录压降试井测试数据。

图3—图5分别为本文模型、三区复合模型[4]和有限元数值模型[12]求取的A井井底压力及压力导数曲线，表1中给出了3种模型拟合解释参数。从曲线拟合程度可以看出，三区复合模型与本文模型拟合效果较好，有限元数值模型拟合效果较差，主要体现在双重介质窜流阶段后存在一个较为明显的线性流阶段，而实测数据中线性流阶段并不明显。从表1对比来看，本文模型给出的解释数据与实测数据更为吻合，且计算时间短，应用方便，而三区复合模型解释的裂缝半长与实测数据相差较大，且无法真实描述基质与压裂裂缝网络之间的流体交换关系，有限元数值模型则需要花费更长的时间进行模拟计算。

图3 A井井底压力及压力导数曲线（本文模型）

图4 A井井底压力及压力导数曲线（三区复合模型[4]）

图5 A井井底压力及压力导数曲线（有限元数值模型[12]）

3 压力传播曲线及影响因素分析

基于控制变量法，参照图2中所用的基础参数值，绘制不同变量数值对应的无量纲井底压力和无量纲井底压力导数与无量纲时间的双对数关系曲线，并分析了裂缝数、裂缝半长、裂缝间距、储容比和窜流系数等参数对井底压力和压力导数曲线的影响。

表1 A井体积压裂段3种模型拟合与实测参数

（1）裂缝数 图6是裂缝数为3，5和7条时的井底压力和压力导数曲线，从图中可以看出，裂缝数对整个井底压力响应阶段都有显著影响，裂缝数越多，无量纲井底压力越低，生产压差越大，单井产能越高，其他条件一定时，增加裂缝数对产量提高效果明显。随着裂缝数增加，生产压差增幅减小，说明对任一特定参数，都有一个裂缝数经济最优值，超出这个最优值范围，盲目增加裂缝数不利于储集层经济开采。

图6 裂缝数对井底压力和压力导数曲线的影响

（2）裂缝半长 图7是无量纲裂缝半长为0.4，0.7和1.0时的井底压力和压力导数曲线，参考长度为200 m.从图中看出，裂缝半长对人工裂缝线性流、双重介质窜流以及第一径向流阶段有影响，裂缝半长越长，初期和中期井底压力传播阶段生产压差越大，初期产量越高，增加裂缝半长对初期产量影响较为明显。就敏感性而言，随着裂缝半长增加，生产压差增幅减小，说明在特定参数条件下，也存在一个裂缝半长最优值，无限追求主裂缝延伸长度是没有意义的。

图7 裂缝半长对井底压力和压力导数曲线的影响

（3）裂缝间距 图8给出了无量纲裂缝间距为0.25，0.45和0.65对应的井底压力和压力导数曲线。从井底压力导数曲线可以得到，裂缝间距对第一径向流和第二线性流阶段井底压力传播有影响，裂缝间距越大，第一径向流阶段作用时间相对增加，第二线性流阶段作用时间相对减少。从井底压力曲线可以看出，裂缝间距对后期生产压差有影响，裂缝间距越大，生产压差越大，产量增幅越小。

图8 裂缝间距对井底压力和压力导数曲线的影响

（4）储容比 图9展示了储容比为0.01，0.05和0.10时的井底压力和压力导数曲线，从图中可以看出，储容比对初期人工裂缝线性流及双重介质窜流阶段有影响，储容比越小，窜流现象越明显，无量纲井底压力导数曲线下凹越明显。

图9 储容比对井底压力和压力导数曲线的影响

（5）窜流系数 图10给出了窜流系数为10，50和100时的井底压力和压力导数曲线，从图中可以看出，窜流系数只影响双重介质系统窜流发生的时间，窜流系数越小，窜流发生的越晚。

图10 窜流系数对井底压力和压力导数曲线的影响

4 结论

（1）针对当前多区复合解析和半解析模型不能准确反映储集层渗流特征的问题，基于压力叠加原理建立了箱式封闭边界裂缝性致密油藏体积压裂水平井压力动态分析半解析模型，将渗流过程划分为6个阶段：人工裂缝线性流、双重介质窜流、第一径向流、第二线性流、拟径向流和封闭边界流阶段。

（2）实例应用表明，本文模型相比于前人模型，具备计算时间短、拟合效果好、解释参数结果更符合实际情况等特点。

（3）本文详细分析了裂缝数、裂缝半长、裂缝间距、储容比和窜流系数对各渗流阶段的影响，裂缝数影响最为显著，其次是裂缝半长、窜流系数、裂缝间距和储容比。

符号注释

B0——体积系数，m3/m3；

CD——无量纲井筒储集系数；

ct——综合压缩系数，MPa-1；

h——储集层厚度，m；

hD——无量纲储集层厚度；

i，j——分别为第i条和第j条人工裂缝；

k，n——变量；

K（0x）——零阶第二类变形贝塞尔函数；

Kf——裂缝渗透率，mD；

Km——基质渗透率，mD；

Lf——参考长度，m；

N——人工裂缝总条数；

p——任意点地层压力，MPa；

p͂——Laplace空间下地层压力，MPa；

pD——无量纲压力；

pf——裂缝系统压力，MPa；

p͂f——Laplace空间下无量纲裂缝压力；

pi——原始地层压力，MPa；

pm——基质系统压力，MPa；

p͂point——Laplace空间下无量纲点源压力；

p͂wD——Laplace空间下无量纲井底压力；

pwDi——第i条人工裂缝压力，MPa；

p͂wDi——Laplace空间下第i条人工裂缝压力，MPa；

p′wDij——第j条人工裂缝在第i条人工裂缝处产生的压力导数；

p͂wDij——Laplace空间下第 j条人工裂缝在第 i条人工裂缝处产生的压力降，MPa；

p͂wDN,N——Laplace空间下第N条人工裂缝第N个系数；

q——体积流量，m3d；

q͂——Laplace空间下体积流量，m3d；

q*——基质系统流向裂缝系统的体积流量，m3d；

q(t)——实时体积流量，m3d；

q0——累计体积流量，m3d；

q͂0(s)——Laplace空间下累计体积流量，m3d；

qD——无量纲体积流量；

qDj——第j条裂缝体积流量，m3d；

q͂Dj(s—)—Laplace空间下第j条裂缝体积流量，m3d；

qref——参考体积流量，m3d；

r——泄流半径，m；

rD——无量纲泄流半径；

s——Laplace变量；

Sk——无量纲表皮因子；

t——时间，s；

tD——无量纲时间；

V——储集层体积，m3；

x，y，z——分别为x，y和z方向位置，m；

xD，yD，zD——分别为x，y和z方向无量纲位置；

xeD，yeD，zeD——分别为x，y和z方向无量纲边长；

xf——裂缝半长，m；

xfD——无量纲裂缝半长；

xwD，ywD，zwD——分别为井口无量纲x，y和z坐标；

xwDi，ywDi，zwDi——分别为第i条人工裂缝无量纲x，y和z坐标；

xwDj，ywDj，zwDj——分别为第j条人工裂缝无量纲x，y和z坐标；

y͂D1，y͂D2——Laplace空间下y方向坐标；

α——形状因子，m-2；

δ(x)——狄拉克函数；

η——导压系数，μm2· MPa/(mPa· s)；

λ——窜流因子，无量纲；

μ——流体黏度，mPa· s；

τ——积分变量；

ϕ——孔隙度，无量纲；

ω——储容比，无量纲。

下标：

f——裂缝参数；

m——双重介质基质参数。

［1］ 张君峰，毕海滨，许浩，等.国外致密油勘探开发新进展及借鉴意义［J］.石油学报，2015，36（2）：127-137.ZHANG Junfeng，BI Haibin，XU Hao，et al.New progress and refer⁃ence significance of overseas tight oil exploration and development［J］.Acta Petrolei Sinica，2015，36（2）：127-137.

［2］ 刘雄.致密油储层体积改造产能评价方法研究［D］.北京：中国地质大学，2013.LIU Xiong.The research of deliverability evaluated for volume re⁃construction in tight oil reservoir［D］.Beijing：China University of Geosciences，2013.

［3］ 苏玉亮，王文东，盛广龙.体积压裂水平井复合流动模型［J］.石油学报，2014，35（3）：504-510.SU Yuliang，WANG Wendong，SHENG Guanglong.Compound flow model of volume fractured horizontal well［J］.Acta Petrolei Sinica ，2014，35（3）：504-510.

［4］ 杨俊峰，芮捍东，田建波，等.致密油藏多段压裂水平井初始产能影响因素分析［J］.石油地质与工程，2014，28（6）：65-68.YANG Junfeng，RUI Handong，TIAN Jianbo，et al.Influencing fac⁃tors analysis of muti⁃stage fractured horizontal wells initial produc⁃tivity in dense reservoirs［J］.Petroleum Geology and Engineering，2014，28（6）：65-68.

［5］ 杨俊峰.致密油藏压裂水平井生产动态分析方法［J］.石油地质与工程，2013，27（5）：85-88.YANG Junfeng.Analysis on fractured horizontal wells performance in tight oil reservoirs［J］.Petroleum Geology and Engineering，2013，27（5）：85-88.

［6］ SHOJAEI H，TAJER E S.Analytical solution of transient multi⁃phase flow to a horizontal well with multiple hydraulic fractures［R］.SPE 165703，2013.

［7］ 姬靖皓，姚约东，马雄强，等.致密油藏体积压裂水平井不稳定压力分析［J］.水动力学研究与进展，2017，32（4）：491-501.JI Jinghao，YAO Yuedong，MA Xiongqiang，et al.Pressure transient analysis for volume⁃fractured horizontal well in tight oil reservoirs［J］.Chinese Journal of Hydrodynamics，2017，32（4）：491-501.

［8］ STALGOROVA K，MATTAR L.Analytical model for unconvention⁃al multifractured composite systems［J］.SPE Reservoir Evaluation&Engineering，2013，16（3）：246-256.

［9］ WANG C，WU Y S.Modeling analysis of transient pressure and flow behavior at horizontal wells with multi⁃stage hydraulic fractures in shale gas reservoirs［R］.SPE 168966，2014.

［10］ 陆程，刘雄，程敏华，等.页岩气体积压裂水平井产能影响因素研究［J］.特种油气藏，2014，21（4）：108-112.LU Cheng，LIU Xiong，CHENG Minhua，et al.Influence factors analysis of productivity for horizontal wells with simulation reser⁃voir volume in shale gas reservoirs［J］.Special Oil&Gas Reser⁃voirs，2014，21（4）：108-112.

［11］ 彭晖，刘玉章，冉启全，等.致密油储层水平井产能影响因素研究［J］.天然气地球科学，2014，25（5）：771-777.PENG Hui，LIU Yuzhang，RAN Qiquan，et al.Study on the horizon⁃tal well production in tight oil reservoirs［J］.Natural Gas Geosci⁃ence，2014，25（5）：771-777.

［12］ 任龙，苏玉亮，郝永卯，等.基于改造模式的致密油藏体积压裂水平井动态分析［J］.石油学报，2015，36（10）：1 272-1 279.REN Long，SU Yuliang，HAO Yongmao，et al.Dynamic analysis of SRV⁃fractured horizontal wells in tight oil reservoirs based on stimulated patterns［J］.Acta Petrolei Sinica，2015，36（10）：1 272-1 279.

［13］ MEDEIROS F，KURTOGLU B，OZKAN E，et al.Pressure⁃trasient performance of hydraulically horizontal well in locally and globally naturally fractured formations［C］.The International Petroleum Technology Conference.Dubai：International Petroleum Technolo⁃gy Conference，2007：1-10.

［14］ 刘雄，田昌炳，姜龙燕，等.致密油藏直井体积压裂稳态产能评价模型［J］.东北石油大学学报，2014，38（1）：91-96.LIU Xiong，TIAN Changbing，JIANG Longyan，et al.Steady deliv⁃erability evaliation model of fracture network reconstruction verti⁃cal well in tight oil reservoir［J］.Journal of Northeast Petroleum University，2014，38（1）：91-96.

［15］ 刘雄，田昌炳，万英杰，等.裂缝性致密油藏直井体积改造产能评价模型［J］.现代地质，2015，29（1）：131-137.LIU Xiong，TIAN Changbing，WAN Yingjie，et al.Deliverability evaliation model of fracture network reconstruction vertical well in tight oil reservoir［J］.Geoscience，2015，29（1）：131-137.

［16］ 王军磊，位云生，程敏华，等.页岩气压裂水平井生产数据分析方法［J］.重庆大学学报，2014，37（1）：102-109.WANG Junlei，WEI Yunsheng，CHENG Minhua，et al.A method of production data analysis for multi⁃fractured horizontal well in shale gas reservoir［J］.Journal of Chongqing University，2014，37（1）：102-109.

［17］ 葛家理，宁正福，刘月田，等.现代油藏渗流力学原理［M］.北京：石油工业出版社，2003：189-194.GE Jiali，NING Zhengfu，LIU Yuetian，et al.The modern mechan⁃ics of fluids flow in oil reservoir［M］.Beijing：Petroleum Industry Press，2003：189-194.

［18］ STEHFEST H.Numerical invesion of Laplace transforms［J］.Com⁃munications of the ACM，1970，13（1）：47-49.