基于分裂合并的多模型拟合方法在点云分割中的应用
张良培,张 云,陈震中,肖佩珮,罗 斌
武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079
数字摄影测量三维构象采用多个视角拍摄的图像来实现三维场景模型的恢复,是构建智慧城市[1]的重要基础技术之一。通常,由大量大范围航拍影像或者高分辨率影像所进行多视重构获得的场景三维点云数据量较大、结构复杂,首要解决的关键性问题是需要对点云进行分割处理。
点云经过分割处理,复杂的点云数据将会被分割成各个简单的几何图元[2-3],通过对简单几何图元的识别和组合,逐步构建复杂的三维模型,进而实现精细化的三维构象。因此三维点云的分割是实现三维构象的重要基础[4]。
点云数据分割方法总体上可以归类为模型驱动和数据驱动两种[5]。其中模型驱动方法作为一种自顶向下的方法,首先建立图元库,再将点云中建筑物与预先定义的图元进行匹配,从而获得图元分割结果。而基于数据驱动的点云分割方法,通过点云数据的各类特征实现对点云的分割。文献[6]证实了在点云屋顶面分割情况下,模型驱动的方法能够保证拓扑关系的正确性但在细节上难以保证。基于数据驱动的点云分割方法又可以大致分为[7]:基于边缘的分割方法[8-9]、基于区域生长的分割方法[10-15]、基于特征的分割方法[16-20]、基于图的分割方法[21-24]、基于模型的分割方法[25-31]及混合方法[32-35]。
通常基于边缘的分割算法通过检测点云数据中隐藏的边缘信息来得到分割区域,此类方法中点云的边缘定义点云强度变化或者表面法向量变化较大的区域。类似于图像边缘检测,文献[8]提出了利用梯度进行边缘检测,通过检测出的三维直线对点集进行拟合,最后基于点云法向量的方向进行强度变化的检测;文献[9]采用了一种基于扫描线的边缘检测器算法,该算法给出了最优边缘检测的定义,提供了保证边缘强度的方法原理和几何解释。基于边缘的分割算法分割速度快,但是点云数据在提取边缘时容易受噪声和点云密度影响,其抗噪能力差,难以适用于结构较为复杂的点云分割处理,实际应用中并不常见。
基于区域生长的方法通常是首先选取种子面,以此作为起始点,通过比较邻域内各个点与种子面的相似程度,对各个种子面周围的离散点云进行分组,不断向外扩展,最终实现完全划分。这类算法最早由文献[10]提出,其关键主要包括种子面的选取及生长规则。选取种子面通常是采样测试任意一个未分类的点,判断该点邻域内能够拟合为平面的点的数目是否达到最少标准,如果是,则这些点构成种子表面。生长规则是通过比较坡度、曲率和曲面法向量等相似度来判断是否进行生长。这类方法对噪声和离群点不敏感,鲁棒性强,适合大规模复杂场景的分割处理,但是受初始选取的种子曲面影响较大,种子曲面选取不当很容易造成巨大的分割误差。并且会收到生长规则的制约,生长规则直接决定分割结果,但是很多情况下,生长规则的选取难以符合数据中包含的所有图元属性。
基于特征的分割方法主要是采用点云所表现出来的几何结构特征或者空间分布特征来对点云进行特征聚类,得到分割结果。其中文献[16]采用了纹理特征来对点云数据进行描述,通过特征聚类来对点云数据进行分割;文献[18—19]则采用法向量和颜色信息作为特征;文献[20]则利用表面法向量实现对点云的实时平面分割。基于特征的分割方法由于将点云分割问题转换到特征空间的聚类问题进行处理,其分割结果不受点云空间分布影响,但是同时其分割结果取决于所采用的特征以及聚类方法,特征描述的好坏直接决定最终的分割效果,并且通常随着点云数量的增加,时间消耗较大,当采用较多维数的特征时,时间效率很低,所以此类方法难以用于点云规模较大的分割处理。
基于图的分割方法是将点云数据当作顶点,利用点的空间邻域关系构造边,利用邻域点的相似性对连接边进行加权,构造成图,利用图割[22,24]的方法实现点云的分割。基于图的分割方法通常采用全局优化的策略进行求解,能够获得全局的优化结果,并且不受数学模型和场景复杂程度的影响,但是由于点云的数据量大,构造的图通常异常复杂,进行优化计算时通常时间复杂度较高。
基于模型的分割方法通常采用简单几何图元的数学参数模型最为先验信息,通过验证点云对模型参数的符合程度,将点云划分到相应的图元类别之中,实现分割处理。其中最为典型的就是采用随机抽样一致性RANSAC[25]的方法进行的点云分割处理。首先对点云数据进行采样,计算每组采样集的模型参数(直线、圆和平面等),然后统计各个点到模型的距离(模型残差),通过设定内点阈值将距离小于阈值的点作为其内点,在一轮大量采样之后选择内点数最多的模型最为提取结果,其内点即为提取模型对应的分割结果。如此完成一次分割过程,通过循环执行RANSAC来不断在剩余的点集中分割出模型,最终实现整个数据集合的分割。基于模型的分割方法基本上都是在RANSAC的基础上改进而来,其中文献[26]对比分析了扩展的RANSAC方法和3D Hough变化方法在Lidar点云的屋顶面提取的效果;文献[27]采用改进的RANSAC分割网格,并实现对符合多种模型的点云进行的同时分割;文献[28]在提出一种自适应的RANSAC方法,通过引入距离、标准差、法向量等信息,来保证最终对屋顶面点云分割效果的拓扑关系的正确性;文献[31]将RANSAC融入其提出的基于局部采样和统计推理的点云分割算法之中来实现点云数据中的平面、圆柱体和曲面分割。基于模型的分割方法由于采用图元的数学参数模型来对点云进行分割,采用几何原理及数学公式进行参数解算,能实现更加高效、快捷的计算。采用几何图元参数模型实质上是对局部点云的抽象降维处理,能够将大量的点云数据表示成简单的图元模型参数,一方面方便点云数据的处理,另一方面能够实现点云数据的高效压缩,为后续的点云存储管理提供便利。并且将海量的点云数据经过这类方法处理后,能够转化成即为规则的简单图元组合,能够实现后续的拓扑分析。不仅如此,基于模型的分割方法具有较强的抗噪能力和对离群点具有较强的鲁棒性,可实现对海量点云数据的分割处理。
目前绝大多数的基于模型的点云分割方法基本上是依据RANSAC的方法改进而来,RANSAC作为一种经典的单模型拟合方法,通过“拟合-剔除”的策略(拟合出一个图元模型后剔除其内点,在剩余点集中再使用RANSAC)来实现对多个模型的提取分割。而基于RANSAC的多模型拟合方法Sequential RANSAC[36-37]和Multi-RANSAC[38],在模型数目较多时,伪离群点的数量急剧增加,多数情况下难以实现较好的分割结果。并且基于RANSAC的分割方法很大程度上没有考虑点云的空间信息,即属于同一个分割子集的点通常情况下是空间相邻的,在多数情况下会导致过分割。不仅如此,采用类似RANSAC的“拟合-剔除”策略进行分割时,如果前一次的分割结果出现误差,会影响后续的分割结果,一次分割结果的好坏很大程度上依赖于内点的阈值。因此,本文采用了基于分裂合并的多模型拟合方法,首先采用基于邻域的采样策略,生成假设模型,如此利用点云数据的较强空间相关性的特性(空间相邻的点属于同一个分割区域的可能性较大),获得较好的模型采样结果。然后在生成的假设模型上统计模型内点,接下来在各个假设模型的模型内点集合,分别进行基于邻域的假设模型生成,从而实现一个假设模型分裂成若干个假设模型,此时采样获得的假设模型不仅包含有空间的先验,还包含模型空间的先验(假设正确的模型内点被包含在同一假设模型的可能性越大),由此获得更加准确的模型采样。最后采用最小残差分组的策略来实现属于不同模型内点的分割处理,由此实现多个模型内点的同时分割,并且最大限度的排除离群点的干扰,获得准确的模型内点分割结果,即作为最终的点云分割结果。
一般而言,通过拟合平面和柱面基本可以满足室内场景点云分割需求。但在模型拟合过程中,平面和柱面的拟合过程经常相互干扰:当存在过分割时,一个完整柱面会被拟合为大量平面;而当出现欠分割情况时,平面会被拟合为半径巨大的圆柱。因此,在多模型拟合过程中,往往需要经过多次检验和判断,实现对平面和柱面的合理划分。对此,本文通过先对点云数据分割成细部后进行平面拟合,将拟合出过多平面模型的区域置为问题区域进行二次判断,以确定是否有柱面出现。通过这种方法减轻平面和弧面的相互干扰程度。
进一步,本文提出了一套基于模型拟合方法的室内点云分割流程。由于点云数据通常存在大量的冗余,并且具有较强的空间相关性,即空间相邻的点云很可能属于同一分割区域。并且在采用基于模型的方法进行分割时,点云的这种分布特性异常显著。因为简单几何图元的模型参数计算通常仅需要几个点即可完成,例如直线需要2个点计算出一组参数,圆需要3个点,平面需要3个点。因此,在拟合平面阐述时仅需要极少的点即可完成,当需要拟合出较为准确的模型参数时,其所需点数相对于点云数据而言也是极少的,并且这种较强的空间关系更有利于拟合出准确的图元模型参数。因此,首先可对原始点云数进行低采样率降采样后,利用基于密度的聚类算法对点云进行预分割。在预分割后的子集上,借由分裂合并的多模型拟合方法探测平面。对问题区域,判断拟合圆柱面,获得对降采样点云的分割结果。最后将原始点云依照距离判断和临近关系判断分配到拟合出的模型上,最终实现对室内点云的分割。相对于其他对比试验方法,此流程在时间开销以及内存要求上表现优异。同时,拟合效果也远优于目前常用在点云分割上的RANSAC类方法和其他的多模型拟合方法。
以下首先介绍基于分裂合并的多模型拟合方法的基本原理和方法流程,然后采用本方法针对实际的点云分割处理进行试验,通过传统MeanShift和MultiRANSAC方法的比较,分析本文提出方法的特点,最后对本文内容进行总结。
1 点云分割方法
本文所采用的基于分裂合并的多模型拟合方法来进行点云分割,首先为了加快点云分割的速度,采用基于密度的聚类方法首先进行点云的预分割处理,然后采用分裂合并的多模型拟合方法进行精细化的分割,最后当需要处理圆柱等典型几何图元分割时,采用切片技术进一步对结果进行整合处理。以下分别从这三个方面进行详细的阐述。
1.1 基于密度聚类实现预分割
点云分布往往具有不均匀性。针对室内点云,由于数据采集过程中,在不同模型接连处,由于反射、遮挡等往往数据密度易受影响,而同一模型的数据密度则较为稳定。在经过较低采样率采样过后,这个差异被进一步增强,数据点之间密度差异性增大。
DBSCAN(density-based spatial clustering of applications with noise)[39]算法作为一种基于密度的聚类算法,通过考察样本分布密度,来实现对样本可连续性的判断,并基于可连接样本,不断扩展聚类簇,最终获得聚类结果。DBSCAN算法可以将附近的点分为一组,并标记出分布密度低的,远离其他数据点的噪声点。
DBSCAN算法流程如下:
(1) 遍历样本集D={x1,x2,x3,…,xm},计算ε-邻域,若样本xi的ε-邻域,内至少包括Minpts个样本,则将xi设为核心对象,加入核心对象集合Ω,且称该点ε-邻域内的其他点相对于xi密度直达。
(2) 随机选取一个核心对象o∈Ω,则该核心对象与该核心对象的所有密度相连点,构成聚类簇Ck;将该聚类簇中所有点,从样本点中和核心对象集合中剔除。
(3) 循环步骤(2),直到核心对象集合为空。
(4) 算法结束,样本集被划分为聚类簇。部分密度过小的数据点,被划分为噪声。
1.2 基于分裂合并的多模型拟合方法
分裂合并的多模型拟合方法主要包括两部分:假设模型的生成和模型的分裂组合过程。在模型生成阶段,采用较大阈值,获取初次分割的模型;在模型分裂阶段,使用更为严苛的阈值,在初次分割的模型基础上进行二次分裂,获得子模型,分割过程可能经过多次重复。最后对所有子模型进行判断,选择最优模型,作为输出。
1.2.1 假设模型的生成
假设模型的生成是通过选择足够多数目的邻域点来计算得出模型。通过迭代选择数据中在一定阈值内邻域点数目最多的点集(密度最大的邻域点集)计算出模型并统计其内点,然后剔除内点在剩下的点集中重复以上步骤,直至没有模型能够提取出来。
假设d为数据集X:={xi|xi∈Rd}i=1,…,n,模型计算函数为F(θ,x)=0,r=RF(θ,x)为模型θ的残差计算函数。
定义数据集X上的最佳拟合模型
(1)
其内点集计算如下
(2)
其中TI为内点阈值
(3)
式(3)为离点x距离小于TN的邻域点集.定义阈值为TN的最密集邻域点集为
(4)
假设模型生成算法描述如算法1所示。其中MPF(minimum points needed for fitting)为拟合参数所需做少数据点的个数。
算法1 假设模型生成HS=HG(X,TN,TI,MPF):
1. 输入数据X0=X,初始化假设模型HS=φ,i=0;
2. while card(X0)≥MPF;
3. 按照式(3),以TN为阈值,找出点集X0中最密集的邻域点集DX0,TN;
4. if card(DX0,TN) 5. 将DX0,TN代入式(1)、式(2),计算模型内点ISDX0,TN,令MIS=DX0,TN; 6. while MIS≠ISDX0,TN; 7. 将MIS代入式(1)、式(2),计算模型内点ISMIS,令ISDX0,TN=ISMIS; 8. end while; 9. if card(ISDX0,TN)≥MPF; 10.i=i+1,hsi=ISDX0,TN; 11. end if; 12.X0=X0-ISDX0,TN; 13. end while; 14. 输出假设模型集合HS={hs1,…,hsi,…,hshn}。 1.2.2 自上而下的分裂与最小残差分组 自上而下的模型分裂其实就是将模型生成过程迭代用于生成的模型。即在原始的数据集中首先采用较大的阈值TN、TI获得第一次的所生成的模型(模型内点组成的集合)。然后分别在所生成的各个模型上采用较小的阈值TN、TI,进行更小粒度层次的模型生成。这个过程即可看作是模型的分裂生成,通过不断地迭代细分,不断地将交叠的模型分离开,将模型内点与外点尽量分离开,获得尽可能包含残差小的内点的集合,以便最终采用最小残差一致的准则进行模型内点的划分,即最小残差分组。经过反复的试验,通常设定合适TN、TI阈值只需两步的分裂过程。详细的算法框架如图2所示。 算法首先采用模型生成在原始数据集hn上获得假设模型HS={hs1,hs2,…,hshn},接下来在每个获得的假设模型hsi上分别继续使用模型生成算法,对于每个假设模型hsi都可以获得生成的假设模型HSi=P{hsi,1,hsi,2,…,hsi,hni},对于最初生成的假设模型HS,两步分裂后最终获得THS={hs1,hs2,…,hshn}。两步模型生成过程中阈值(TN1,TI1)与(TN2,TI2)是不同的,通常(TN2,TI2)要比(TN1,TI1)小。最后最小残差分组(图3)利用各个模型计算的残差向量对各个数据点进行最小残差分组。最终获得模型内点按照模型大小降序排列{mλ(1),…,mλ(t)}。即可选择所需要求得的前K个模型作为最终的结果。 图1 算法流程Fig.1 The workflow of the whole algorithm 最小残差分组首先计算出由两步分裂获得的各个模型对应整个数据的残差集合,方法如下 (5) 计算出所有模型的残差之后即可获得各个数据对应不同模型的残差值,统计如果数据对应的最小残差值对应模型I,则将该数据标记为模型I的内点。依次如此对所有数据进行最小残差值的分组,将整个数据集划分成不同的内点集合。最后按照内点集合的大小降序排列,取出前K个模型作为所求模型输出,K为所需求解模型个数。 算法的具体描述如算法2所示。 算法2 最小残差分组{mλ(1),…,mλ(t)}=MRG(X,THS,TI,MPF): 1. 输入数据X0=X,初始化模型集合M=φ,RS=φ,k=0; 2. fori=0 to hn; 3. forj=0 to hni; 4. hst=hsi,j,将hst代入式(2)和式(4),计算模型参数和残差TmpR; 5.k=k+1,Rk=TmpR; 6. end for; 7. end for; 8. TN=k,RS={R1,…,Rm}; 10. 令m1=φ,…,mTN=φ; 11. fori=0 ton; 13. ifri,tem=∞,xi为外点; 14. elsemtem=mtem∪{xi}为外点; 15. end for; 16. 将集合{m1,…,mTN}按照大小降序排序,并删除小于MPF的集合,获得{mλ(1),…,mλ(t)}; 17. 输出模型内点集合M={mλ(1),…,mλ(t)}。 数据分布中,模型所属的数据点分布,往往较噪声的数据点分布要更为密集,通过查找数据点的最密集分布区域,进行采样,可以明显提高采样质量,进而提升生成的假设模型质量。假设模型质量的提升,不仅意味着对所需生成假设模型数量的减少,也意味着后期在正确的模型生成的过程难度降低。对于拟合结果以及拟合效率都有积极意义。而通过分裂合并的方法,降低了算法的时间复杂度。 由于在DBSCAN算法中,已经将点云数据分成较为细碎的区域,大多数区域内的真实模型数目得到控制。在经过多模型拟合后,当模型与真实模型一致时,拟合出的模型数目保持较低。而当预设的模型与真实模型一致时则可能出现意外。例如当用平面,对圆弧面进行拟合,完整的圆弧面会被拟合成大量的平面。对此,本文将拟合出过多平面的子区域,设为问题区域,获取点集X,进行二次判断,以探测柱面目标。 本文提出点云切片技术,对柱面模型进行拟合。由于柱面模型更为复杂,在柱面判断和拟合过程中直接进行圆柱模型的拟合,往往会带来较多的时间损耗。通过将点云进行切片,三维的圆柱模型拟合转换为一系列的二维圆形拟合,可以改善这一效率。将兴趣区域进行多层的分割,取薄层,投影到二维方向,进行椭圆检测。当圆柱垂直于投影方向,则可以拟合出多个同心圆,将一系列圆弧组合,圆心的连线方向即为圆柱的轴向,圆弧半径即为圆柱半径;而当圆柱区域相对于投影方向有夹角,则会拟合出一系列椭圆,椭圆的短半轴即为圆柱的半径,椭圆圆心的连线方向即为圆柱轴向,借此可以实现对圆柱的拟合。 通过在xy、yz、xz三个方向上的投影,则问题区域点云中的圆柱最终可以被拟合出来。 图2 不同切割方法Fig.2 Different cut methods 试验选取了加利福尼亚大学伯克利分校的科里厅的部分走廊数据(http:∥www-video.eecs.berkeley.edu/research/indoor/)进行试验。试验数据如图3所示,其中区域A、B、C3个区域的复杂性不断增加。 区域A是一个I字形状走廊,走廊一侧分布有子空间,可能是由于台阶入口等导致。区域B是两个走廊的连接处,包括两个走廊的部分点云。其连接部分外侧为直角,内侧为平面,且部分区域的扫描数据受到了开关门的影响。区域C分布更为复杂,不仅包括了两段走廊,同时拐角区域的内侧为圆柱面,且由于圆柱面区域较大,平面区域与圆柱面区域在拟合过程中相互影响,需要加以考虑。 试验数据如图3所示。 图3 试验数据Fig.3 Test data 图4和5分别为区域A、B在MeanShift[40]、MultiRANSAC方法和本文所提出方法下的试验结果。 可以看出,在区域A中,MeanShift和MultiRANSAC方法对于较小的面片区域都出现了丢失。其中MeanShift方法更为明显,而MultiRANSAC方法主要是对屋顶装饰面片的丢失,本文方法则较好地保留了这些面片。在区域B中,MeanShift无法实现对拐角的划分,MultiRANSAC方法与本文方法试验效果类似。 图4 区域A 3种方法分割结果Fig.4 Experimental results on area A 图5 区域B 3种方法分割结果Fig.5 Experimental results on area B 同时,对比3种算法的耗时,如表1所示。针对区域A和区域B,MeanShift方法由于是对点云数据进行的聚类分割,运算量较大,耗时最多。多模型拟合方法MultiRANSAC虽然是对Sequential RANSAC的改进,但是需要采样计算模型参数,而且每次采样获得若干模型参数后,需要对模型之间进行相似性比较,其收敛过程较慢,时间消耗虽低于MeanShift方法,但是依然较高。本文提出的方法仅需要经过两次的采样过程计算模型参数,统计模型内点,最后只需要采用最小残差进行分组,运算复杂度低,实际的计算速度也是较快的,时间消耗上明显优于另外两个经典方法。 表1 算法耗时 而当在区域C进行分割时,容易发现MeanShift和MultiRANSAC算法与本文方法产生了更大的效果差距。受到圆柱区域的影响,MeanShift方法和MultiRANSAC方法只能够对明显的两个大直线区域进行拟合,而靠近圆柱一侧的平面完全无法拟合。由于MeanShift算法依靠距离最小原则将原始点云分配到各计算模型中后,得到最终的分割结果。 依据距离准则对数据进行判断后,将原始点云分配到各个模型上,获得最终的试验结果如图6 所示。 图6 区域C 3种方法分割结果Fig.6 Experimental results on area C 表2中展示了3种算法分别在区域A、区域B和区域C上的分割正确率(正确的分割点个数除以总的点个数),其中本文方法在3个区域的分割正确率均高于其他两种方法,其中由于MeanShift在分割过程中会或多或少的丢失掉一些分割区域,分割不完整,并且在相近的平面分割时会出现欠分割;而MultiRANSAC方法则相反,在很多区域存在过分割状况,分割结果存在很多破碎的细小分割区域。该方法在较大区域上能够实现完整的分割,过分割的现象不严重,即是一些细小的区域也能实现较好分割。特别是针对曲面也能实现较完整的分割。 表2 区域分割正确率 本文根据点云的分布特点,使用基于密度的聚类对采样结果进行预分割,再使用基于分裂合并的模型拟合方法,在预分割基础上进行模型拟合。对问题区域采用切片方法进行判断和柱面拟合,最终实现对点云的分割。相对于其他模型拟合方法,本文采用的分割方法在保证时间开销较小的同时,自动判断模型数目,且同时实现对柱面模型和平面模型的拟合。同时,应对室内点云分割中模型数量较多,伪噪声点数目巨大的情况,本文的方法也能起到良好作用。三维点云分割经过本文方法处理后,可以有效分割成简单的图元结构,更加有利于实现复杂的三维场景构象。本文所提出的点云分割方法能够有效地将复杂场景三维点云分割成常规的简单几何图元,相较于常规的点云分割算法本文方法提取图元更为准确完整,并且能够实现弧面等较为复杂图元的较为完整的分割提取。相较于常规的点云分割方法,本文方法处理在时间效率上有较大提升,点云分割的正确率要高于常规的分割方法,较为适用于海量点云数据的分割处理。 参考文献: [1] 李德仁, 姚远, 邵振峰. 智慧城市的概念、支撑技术及应用[J]. 工程研究-跨学科视野中的工程, 2012, 4(4): 313-323. LI Deren, YAO Yuan, SHAO Zhenfeng. The Concept, Supporting Technologies and Applications of Smart City[J]. Journal of Engineering Studies, 2012, 4(4): 313-323. [2] SCHNABEL R, WAHL R, WESSEL R, et al. Shape Recognition in 3D Point-clouds[C]∥The 16-th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision’2008. Czech Republic: UNION Agency-Science Press, 2008: 65-72. [3] LI Yangyan, WU Xiaokun, CHRYSATHOU Y, et al. GlobFit: Consistently Fitting Primitives by Discovering Global Relations[C]∥Proceeding of ACM SIGGRAPH. Vancouver, British Columbia, Canada: ACM, 2011: 52. [4] MAHABADI R K, HANE C, POLLEFEYS M. Segment Based 3D Object Shape Priors[C]∥IEEE Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 2838-2846. [5] 宫钰嵩. RGBD数据驱动的室内景物三维建模方法研究[D]. 南京: 南京大学, 2015. GONG Yusong. Research on 3D Modeling of Indoor Objects and Scenes Based on RGBD Data[D]. Nanjing: Nanjing University, 2015. [6] DORNINGER P, PFEIFER N. A Comprehensive Automated 3D Approach for Building Extraction, Reconstruction, and Regularization from Airborne Laser Scanning Point Clouds[J]. Sensors, 2008, 8(11): 7323-7343. [7] 秦彩杰, 管强. 三维点云数据分割研究现状[J]. 宜宾学院学报, 2017, 17(6): 30-35. QIN Caijie, GUAN Qiang. Research Status of 3D Point Cloud Data Segmentation[J]. Journal of Yibin University, 2017, 17(6): 30-35. [8] BHANU B, LEE S, HO C C, et al. Range Data Processing: Representation of Surfaces by Edges[C]∥Proceedings of the Eighth International Conference on Pattern Recognition. Paris, France: [s.n.], 1986: 236-238. [9] JIANG Xiaoyi, BUNKE H. Edge Detection in Range Images Based on Scan Line Approximation[J]. Computer Vision and Image Understanding, 1999, 73(2): 183-199. [10] BESL P J, JAIN R C. Segmentation through Variable-order Surface Fitting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 10(2): 167-192. [11] KOSTER K, SPANN M. MIR: An Approach to Robust Clustering-application to Range Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(5): 430-444. [12] ROTTENSTEINER F. Automatic Generation of High-quality Building Models from Lidar Data[J]. IEEE Computer Graphics and Applications IEEE, 2003, 23(6): 42-50. [14] WANG Zhe, LIU Hong, QIAN Yueliang, et al. Real-Time Plane Segmentation and Obstacle Detection of 3D Point Clouds for Indoor Scenes[M]∥FUSIELLO A, MURINO V, CUCCHIARA R. Computer Vision-ECCV 2012. Berlin, Heidelberg: Springer, 2012: 22-31. [15] PAPON J, ABRAMOV A, SCHOELER M, et al. Voxel Cloud Connectivity Segmentation-Supervoxels for Point Clouds[C]∥IEEE Computer Vision and Pattern Recognition. Portland, OR: IEEE, 2013: 2027-2034. [16] FILIN S. Surface Clustering from Airborne Laser Scanning Data[J].International Archives of Photogrammetry and Remote Sensing, 2002: XXXII, 3A:119-124. [17] VOSSELMAN G, DIJKMAN S. 3D Building Model Reconstruction From Point Clouds and Ground Plans[J]. International Archives of Photogrammetry & Remote Sensing, 2001, 34(Part 3/W4): 37-43. [18] ZHAN Qingming, YU Liang, LIANG Yubing. A Point Cloud Segmentation Method based on Vector Estimation and Color Clustering[C]∥IEEE 2nd International Conference on Information Science and Engineering. Hangzhou, China, China: IEEE, 2011: 3463-3466. [19] ZHAN Qingming, YU Liang. Segmentation of LiDAR Point Cloud based on Similarity Measures in Multi-Dimension Euclidean Space[M]∥ZENG D. Advances in Computer Science and Engineering. Berlin, Heidelberg: Springer, 2012: 349-357. [20] HOLZ D, HOLZER S, RUSU R B, et al. Real-Time Plane Segmentation Using RGB-D Cameras[M]∥RÖFER T, MAYER N M, SAVAGE J, et al. RoboCup 2011: Robot Soccer World Cup XV. Berlin, Heidelberg: Springer, 2012: 306-317. [21] SCHOENBERG J R, NATHAN A, CAMPBELL M. Segmentation of Dense Range Information in Complex Urban Scenes[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, Taiwan: IEEE, 2010: 2033-2038. [22] SALLEM N K, DEVY M. Extended GrabCut for 3D and RGB-D Point Clouds[M]∥BLANC-TALON J, KASINSKI A, PHILIPS W, et al. Advanced Concepts for Intelligent Vision Systems. Cham: Springer, 2013: 354-365. [23] GEETHA M, RAKENDU R. An Improved Method for Segmentation of Point Cloud Using Minimum Spanning Tree[C]∥IEEE International Conference on Communications and Signal Processing. Melmaruvathur, India: IEEE, 2014: 833-837. [24] YANG Jingyu, GAN Ziqiao, LI Kun, et al. Graph-based Segmentation for RGB-D Data Using 3-D Geometry Enhanced Superpixels[J]. IEEE Transactions on Cybernetics, 2017, 45(5): 927-940. [25] FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[M]∥Readings in Computer Vision. [s.l.]: Elsevier, 1987: 726-740. [26] TARSHA-KURDI F, LANDES T, GRUSSENMEYER P. Hough-Transform and Extended RANSAC Algorithms for Automatic Detection of 3D Building Roof Planes from LiDAR Data[C]∥Proceedings of the ISPRS Workshop on Laser Scanning, Espoo:ISPRS.2007, 36: 407-412. [27] SCHNABEL R, WAHL R, KLEIN R. Efficient RANSAC for Point-Cloud Shape Detection[J]. Computer Graphics Forum, 2010, 26(2): 214-226. [28] CHEN Dong, ZHANG Liqiang, LI J, et al. Urban Building Roof Segmentation From Airborne Lidar Point Clouds[J]. International Journal of Remote Sensing, 2012, 33(20): 6497-6515. [29] GELFAND N, GUIBAS L J. Shape Segmentation Using Local Slippage Analysis[C]∥Proceedings of Eurographics/ ACM SIGGRAPH Symposium on Geometry Processing. Nice, France: ACM, 2004: 214-223. [30] AWADALLAH M, ABBOTT L, GHANNAM S. Segmentation of Sparse Noisy Point Clouds Using Active Contour Models[C]∥IEEE International Conference on Image Processing. Paris, France: IEEE, 2015: 6061-6065. [31] WANG Yanmin, SHI Hongbin. A Segmentation Method for Point Cloud Based on Local Sample and Statistic Inference[M]∥BIAN F, XIE Y. Geo-Informatics in Resource Management and Sustainable Ecosystem. Berlin, Heidelberg: Springer, 2015: 274-282. [32] MA Teng, WU Zhuangzhi, FENG Lu, et al. Point Cloud Segmentation Through Spectral Clustering[C]∥IEEE 2nd International Conference on Information Science and Engineering. Hangzhou, China: IEEE, 2011: 1-4. [33] NURUNNABI A, BELTON D, WEST G. Robust Segmentation in Laser Scanning 3D Point Cloud Data[C]∥IEEE International Conference on Digital Image Computing Techniques and Applications. Fremantle, WA, Australia: IEEE, 2013: 1-8. [34] WOLF D, PRANKL J, VINCZE M. Fast Semantic Segmentation of 3D Point Clouds Using a Dense CRF with Learned Parameters[C]∥IEEE International Conference on Robotics and Automation. Seattle, WA: IEEE, 2015: 4867-4873. [35] GREEN W R, GROBLER H. Normal Distribution Transform Graph-based Point Cloud Segmentation[C]∥Pattern Recognition Association of South Africa and Robotics and Mechatronics International Conference. Port Elizabeth, South Africa: IEEE, 2015: 54-59. [37] KANAZAWA Y, KAWAKAMI H. Detection of Planar Regions with Uncalibrated Stereo Using Distributions of Feature Points[C]∥Proceedings of the British Machine Vision Conference. [s.l.]: BMVA Press, 2004: 247-256. [38] ZULIANI M, KENNEY C S, MANJUNATH B S. The Multiransac Algorithm and Its Application to Detect Planar Homographies[C]∥IEEE International Conference on Image Processing. Genova, Italy: IEEE, 2005: Ⅲ-153. [39] ESTER M, KRIEGEL H P, SANDER J, et al. A Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise[C]∥Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining. [s.l.]: AAAI Press, 1996: 226-231. [40] COMANICIU D, MEER P. Mean Shift: A Robust Approach Toward Feature Space Analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619.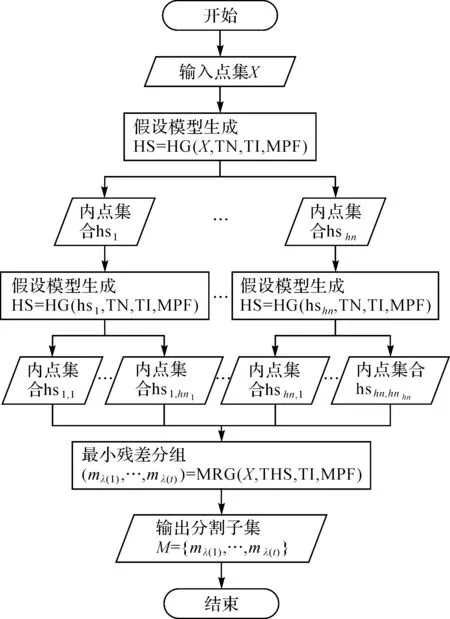

1.3 圆柱模型探测

2 试验结果与分析
2.1 试验数据

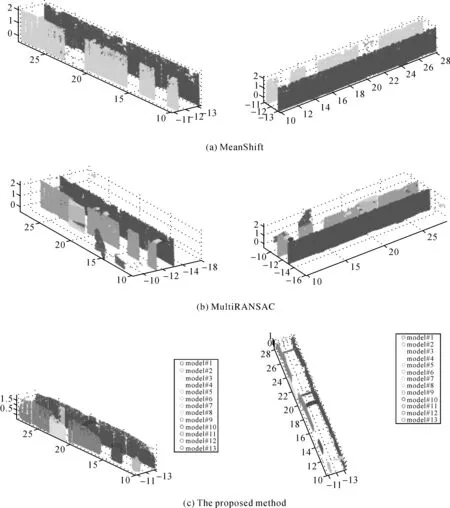
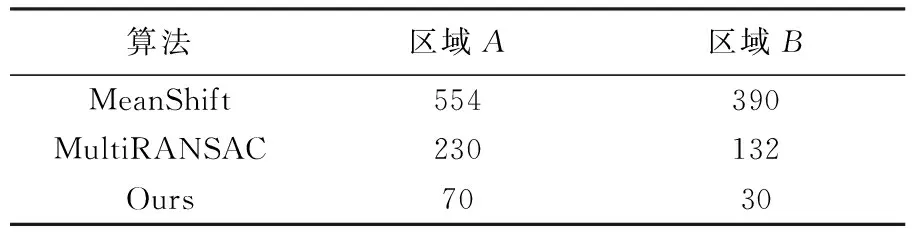
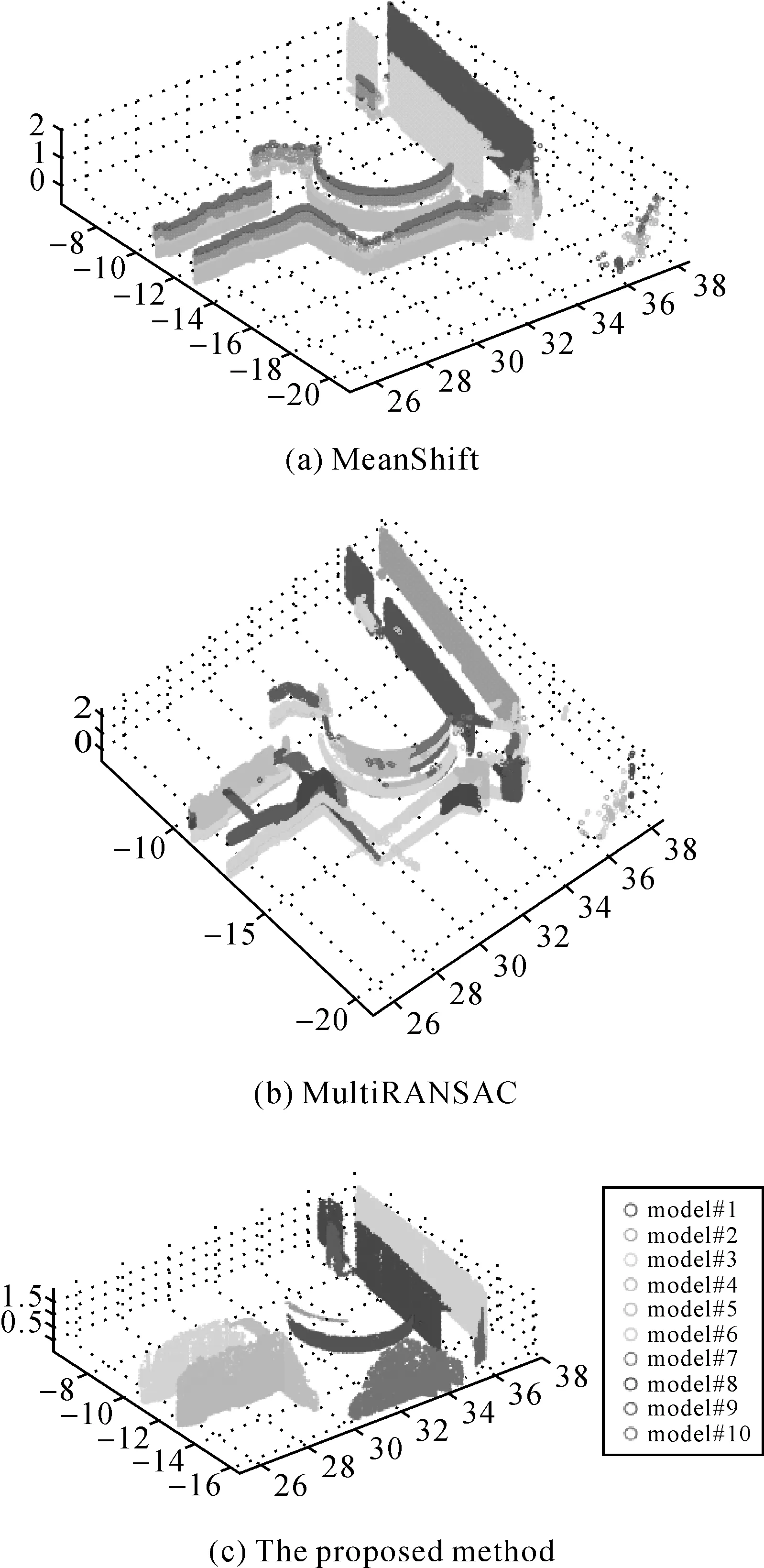
2.2 处理结果


3 总 结

