卫星影像匹配的深度卷积神经网络方法

范大昭，董 杨，张永生

信息工程大学地理空间信息学院，河南 郑州 450001

近年来，遥感信息数据处理进入大数据时代[1-2]，卫星影像呈井喷式涌现，人们对影像处理技术的准确性和时效性提出了较高要求。处理卫星影像的基础性工作之一是进行影像间的匹配。通常的影像匹配思路是：首先进行影像特征点检测，然后进行特征点描述，最后进行描述符间的相似性匹配。传统的影像特征点检测算法主要包括：高斯拉普拉斯(Laplace of Gaussian，LOG)检测算法[3]、Harris检测算法[4]、SIFT(scale-invariant feature transform)检测算法[5]等。常用的影像特征描述符主要包括：SIFT特征描述符及其衍生算法[6-7]、brief特征描述符及其衍生算法[8-9]等。影像描述符间的匹配实现则主要是通过近似最邻近搜索，以找到描述符之间欧氏距离最短的对应特征点[10-11]。针对于描述符能否对具体问题进行自适应优化，可将描述符分为两种：面向结构的描述符和面向对象的描述符。其中，面向结构的描述符是指具有固定流程参数的特征描述符，面向对象的描述符是指能够面向具体问题自适应生成流程参数的特征描述符。传统的手工设计描述符能够在某些方面具有较好的普适表现(如抗尺度变化、抗仿射变化等)，但大多是面向结构的描述符，其对于具体卫星影像中内含的先验模式，很难实现有针对性的优化。在大多数具体问题中，涉及的卫星影像多为单个或数个相机远距离成像拍摄而来，成像对象也多为山区、平地、居民地、湖泊等多种类型，同一类型对象在卫星影像上呈现出一定规律的内蕴模式。若能充分利用这些良好的先验特性，则有望进一步提高卫星影像的匹配正确率与数据处理效率。因此，设计一种面向对象的匹配流程，寻找卫星影像内蕴的先验模式，实现具体问题的自适应处理，以进一步提高卫星影像的匹配丰富度与准确率，具有重要的研究意义。

当前，随着计算机软硬件水平的提升，深度学习方法发展迅猛，在计算机视觉、机器视觉、模式识别等相关领域得到了广泛应用。深度学习方法一般是指利用含多个隐藏层的神经网络模型进行经验数据的自动拟合，得到先验参数，据此实现对新数据的自动处理。深度学习方法是一种典型的面向对象方法，能够针对具体的数据目标进行优化，具有较大的应用潜力。近年来，有不少学者利用深度学习方法进行了影像局部描述符提取的研究。其中，文献[12]利用卷积神经网络模型进行了窄基线下的影像立体匹配研究；文献[13]研究了多种神经网络模型在影像块匹配中的性能；文献[14]则设计了一种MatchNet模型，进行影像特征描述符的提取与匹配。然而，这些研究多是面向较为杂乱的近景影像处理问题，对卫星影像中的匹配问题却少有涉及。

传统的面向结构的影像匹配算法并不能很好地处理异源、多时相及多分辨率卫星影像间的匹配问题。卫星影像相对近景影像，影像目标相对较为单一，内容变化相对简单。本文试图通过深度学习方法，将近年来发展较快的神经网络技术运用到卫星影像特征匹配中，自动学习影像间的匹配模式，实现一种面向对象的卫星影像间自动匹配流程，得到更为丰富和更高准确率的匹配点对。

1 影像特征点匹配算法

1.1 卷积神经网络

早期神经网络也称为多层感知机[15]，在层内使用激励函数进行响应，层间使用全连接进行数据传递，训练中使用反向传播(back propagation，BP)算法[16]进行学习，如图1所示。假设P={p1,p2,…,pn}为层输入，Q={q1,q2,…,qm}为层输出，则在全连接神经网络中对于第i个输出qi，其计算为

(1)

式中，W={w1,w2,…,wn}为权重向量，b为偏差值，f(x)为激励函数。

然而，由式(1)及图1可以看出，随着神经网络层数的不断增加，待训练的网络参数急剧增长，网络参数求解越发困难。针对这一问题，可采用“卷积核”简化神经网络，从而极大缩减待求参数，进一步提高训练过程的鲁棒性，如图2所示。对于二维离散影像I(x,y)，对其利用卷积核f(s,t)进行操作，可得到新影像I′(x,y)，计算式如下

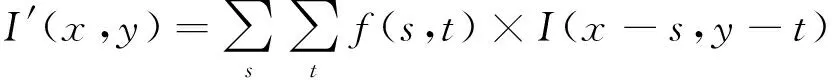
(2)

在卷积神经网络中，利用式(2)代替式(1)中的WTP项，从而可减少待求参数数量，增加整体网络的稳健性。

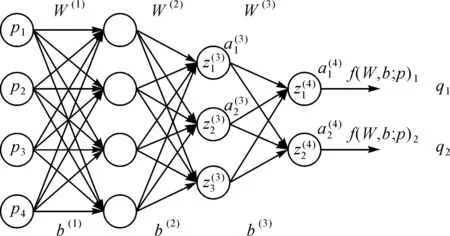
图1 典型全连接神经网络结构Fig.1 Typical fully connected neural network structure

1.2 基于深度卷积神经网络的影像匹配模型

提升卷积神经网络处理性能的方法之一是增加网络层数，形成深度卷积神经网络，已有不少学者对此进行了研究，取得了一些研究成果[17-18]。然而，现有的研究多是针对近景影像，且目标多是影像分类或模式识别，对于卫星影像间的匹配问题少有研究。本文在已有的用于影像分类的神经网络模型基础上，通过模型优化，使新的神经网络模型更加适用于卫星影像匹配，从而实现一种面向对象的影像匹配模型。

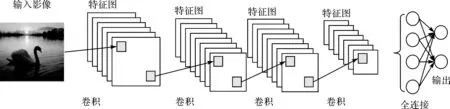
图2 典型卷积神经网络结构Fig.2 Typical convolution neural network structure

1.2.1 两通道深度卷积神经网络

传统意义的影像分类神经网络模型训练分为两部分输入：一是影像数据，二是影像对应的标签数据。前者提供了神经网络的实际输入值，后者提供了神经网络的目标输出值。前者经过前馈网络计算标签输出值，后者结合标签输出值经过后馈网络调整网络参数值，从而实现整体神经网络的不断迭代优化。卫星影像特征点的匹配，实质是进行特征点对局部影像灰度的分析比较，从而判断是否为同名点对。因此，可将待比较的特征点对局部影像看作为两通道影像(彩色影像可看为六通道，原理与两通道相同，下文不再单独论述)，作为神经网络的影像输入值。其中两个通道值分别对应两个待匹配点的局部灰度值。对应的影像数据标签可分为两类：一类是正确同名点对局部影像合成的两通道影像，另一类是错误同名点对局部影像合成的两通道影像。由此，卫星影像的匹配问题可转换为两通道影像的分类问题。

在文献[13]研究成果的基础上，本文设计了两通道深度卷积神经网络(2 channel deep convolution neural network，2chDCNN)，如图3所示。2chDCNN输入数据为待匹配点对局部影像合成的两通道影像，输出数据为1维标量。首先，进行4次卷积和ReLu操作；然后，进行MaxPooling操作；随后，再进行3次卷积和ReLu操作；最后，进行扁平化与两次全连接操作。两通道深度卷积神经网络构建简单、易于训练，能够自动学习卫星影像间的匹配模式，实现了面向对象的匹配过程。但其输入局部影像块为固定大小，在卫星影像尺度学习方面有一定缺陷，还需进一步优化。

图3 两通道深度卷积网络Fig.3 2 channel deep convolution neural network

1.2.2 优化的两通道深度卷积神经网络

结合传统数字摄影测量中特征描述符的提取过程，分析传统特征描述符的抗尺度变换特性，本文在两通道深度卷积神经网络前端，加入空间尺度卷积层，以加强整体网络的抗尺度特性。考虑到sift特征提取过程中，尺度空间是保证sift特征具有良好抗尺度变换特性的重要因素之一。因此，可对输入影像进行金字塔影像生成处理，并加入两层卷积层用于模拟整体尺度空间的生成过程。为保证随后处理过程的简洁，将金字塔影像复制扩展到原始影像维度，如图4所示。这样两通道影像经过金字塔处理变为六通道影像，经过空间卷积层处理变为尺度特征影像，再进行2chDCNN中的深度卷积神经网络处理。在处理过程中，变换后的六通道影像对应标签依然为原始标签值。

图5即为设计的基于空间尺度的两通道深度卷积神经网络(based-spatial-scale 2 channel deep convolution neural network，BSS-2chDCNN)。由于在2chDCNN网络前端加入了空间尺度卷积层，使其能更好地学习局部影像间的尺度模式，增加了整体模型的鲁棒性。

图4 神经网络中影像金字塔过程Fig.4 Image pyramid process in neural network

图5 基于空间尺度的两通道深度卷积网络Fig.5 Based-spatial-scale 2 channel deep convolution neural network

1.3 基于深度卷积神经网络的卫星影像匹配

考虑到之前论述的深度卷积神经网络模型与卫星影像的特殊性，设计如下的卫星影像匹配流程：①特征点检测；②基于卫星辅助参数的特征点对预匹配；③基于神经网络的局部影像模式匹配。具体匹配流程如图6所示。

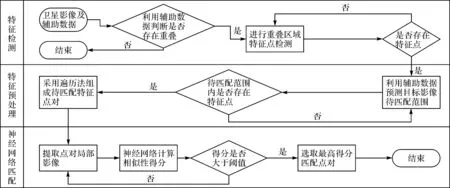
图6 基于深度卷积神经网络的卫星影像匹配流程Fig.6 Satellite image matching process based on deep convolution neural network

上述流程中，步骤①中特征点检测可采用传统的Harris角点检测算子等方法进行实现；步骤②中特征点对预匹配是指利用卫星影像概率地理坐标信息进行匹配点对范围约束，从而缩短整体匹配时间；步骤③中采用深度卷积神经网络对约束范围内的匹配点对进行遍历匹配判断，对于每一点取概率得分最高且大于阈值者为最佳匹配点。

2 试验及结果分析

试验首先着重对深度卷积神经网络模型匹配的可行性进行分析，然后进行实际卫星影像的匹配试验，并设计了与10种传统卫星影像匹配方法的对比试验。试验硬件平台采用Intel i7 CPU、GTX 980M GPU以及16G内存配置，采用Torch7[19]、MXNet(arXiv:1410.0759,2014)及英伟达cuDNN(arXiv：1107.2490,2011)实现具体深度卷积神经网络匹配流程。

2.1 两通道深度卷积神经网络匹配试验

试验采用两组数据，具体参数及部分影像截图如表1及图7所示。GFG数据集中，谷歌影像为高分辨率正射拼接影像，高分四号卫星影像为较低分辨率的原始倾斜影像。由图7可以看出，谷歌及高分四号卫星影像由于分辨率及影像获取环境的不同，同名特征点对相同大小局部区域的影像灰度特征差别较大，采用传统匹配算法进行影像匹配难度较大。由于使用的影像具有不同的空间分辨率，GFG数据集可以较好地验证本文算法提出的空间尺度卷积层的效用。THD数据集为天绘卫星三线阵相机拍摄的影像，可用于进一步验证本文提出模型的有效性。

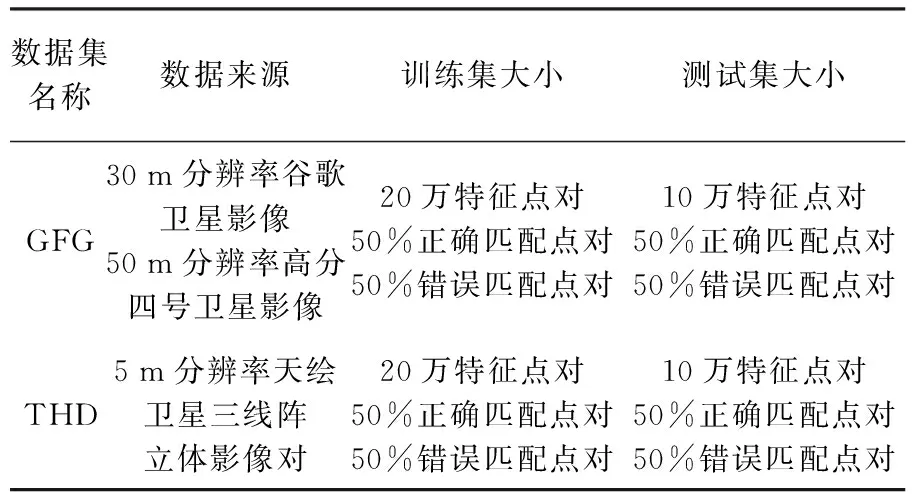
表1 试验数据信息介绍

图7 试验数据部分示意Fig.7 Display of experimental data

试验中提取局部影像块的尺寸为32×32像素，网络训练最大迭代次数设置为100次，训练块大小设置为256，采用ASGD(average stochastic gradient descent)方法[22]进行网络参数优化，学习率设置为0.1，权重下降值设置为0.000 5。

试验中采用TPR(true positive rate)、FPR95(false positive rate at 95% recall)与ROC(receiver operating characteristic)曲线进行模型性能的评估。其中，TPR表征的是模型测试的正确率；FPR95表征的是模型在召回率为95%情况下的错判率(false positive rate，FPR)；ROC曲线横轴为FPR值，纵轴为对应TPR值[21-22]。其中，TPR与FPR的计算公式如下所示

(3)

(4)

图8 GFG训练集TPR统计Fig.8 TPR results of GFG training set

由图8可以看出：利用GFG数据集进行训练时，优化的BSS-2chDCNN模型能够在迭代计算13次后就达到99%的训练集正确率，而2chDCNN模型则要迭代计算74次后才能达到99%的训练集正确率。这说明优化模型中空间尺度卷积层发挥了积极效用，能够迅速地学习影像匹配模式中的尺度因子，从而极大地减少了模型迭代训练次数。由图8可以看出利用GFG数据集进行测试时，优化的BSS-2chDCNN模型相对2chDCNN模型具有较低的FPR95值以及较好的ROC曲线。由此也说明了BSS-2chDCNN模型相对2chDCNN模型具有较好的稳健性。

图9 GFG测试集ROC曲线统计Fig.9 ROC results of GFG test set

利用THD数据集进一步测试BSS-2chDCNN模型，部分计算结果如表2所示。

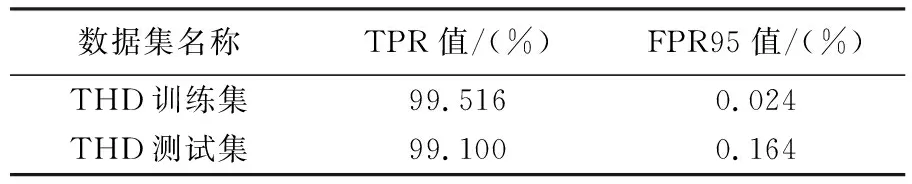
表2 THD数据集试验结果统计

由表2可以看出，本文设计的BSS-2chDCNN模型能够较好地处理THD数据集影像，具有较好的稳健性。这进一步验证了利用深度卷积神经网络进行卫星影像匹配的可行性。

2.2 基于深度卷积神经网络的卫星影像匹配试验

采用某区域高分四号卫星影像与谷歌卫星影像数据进行试验，如图10所示。高分四号卫星影像大小为1625×1625像素，分辨率约为70 m；谷歌卫星影像大小为1855×1855像素，分辨率约为50 m。试验数据为典型的异源、多时相、多分辨率影像，利用其进行对比试验，能够在一定程度上检测本文算法的性能。

试验设计了与多种常用影像匹配方法的对比，包括SIFT特征提取与描述方法[5]、SURF特征提取与描述方法[7]、KAZE特征提取与描述方法[23]、AKAZE特征提取与描述方法[24]、ORB特征提取与描述方法[25]、BRISK特征提取与描述方法[26]、FAST特征提取方法[27]、AGAST特征提取方法[28]、Harris特征提取方法[29]、Shi-Tomasi特征提取方法[30]等。具体对比试验方法设计如表3所示。

图10 匹配对比试验影像数据示意Fig.10 Image data for matching contrast experiment

试验序号特征检测方法描述符生成方法描述符匹配方法1SIFTSIFTANN2SURFSURFANN3KAZEKAZEBF4AKAZEAKAZEBF5ORBORBBF-Hamming6BRISKBRISKBF7FASTSIFTANN8AGASTSIFTANN9HarrisSIFTANN10Shi-TomasiSIFTANN

描述符匹配方法中，SIFT与SURF描述符采用快速近似最近邻(approximate nearest neighbor，ANN)方法进行搜索，利用欧氏距离进行相似性判断；KAZE、AKAZE与BRISK描述符采用暴力搜索(brute force，BF)方法进行搜索，利用欧氏距离进行相似性判断；ORB描述符采用暴力搜索方法进行搜索，利用汉明距离进行相似性判断。在设计的10种试验中，为了便于进行定量对比，基于深度卷积神经网络的卫星影像匹配试验，采用对应特征检测算法进行卫星影像特征点的检测，设置寻找待匹配点的范围大小为51×51像素，得分最低阈值设置为0.9，深度卷积神经网络采用BSS-2chDCNN模型，并利用GFG数据集进行预先训练。最终试验结果如表4及图11至图20所示。

图11至图20中，每张小图上半部分为谷歌卫星影像，下半部分为高分四号卫星影像；图11—20中(a)图为检测到的特征点分布示意图，蓝色点为检测到的特征点，对应表4中的谷歌影像提取特征点数与高分影像提取特征点数两栏；图11—20中(b)图为传统匹配方法得到的匹配点对结果示意图，青色线为匹配特征点对间的连线，对应表4中传统方法匹配数一栏；图11—20中(c)图为基于BSS-2chDCNN方法得到的匹配点对结果示意图，青色线为匹配特征点对间的连线，对应表4中基于BSS-2chDCNN方法匹配数一栏。可以看出，在相同特征检测点的情况下，本文方法能够得到更为丰富的匹配结果。

表4 匹配结果统计信息

图12 SURF对比试验结果Fig.12 Matching results based on SURF

图13 KAZE对比试验结果Fig.13 Matching results based on KAZE

图14 AKAZE对比试验结果Fig.14 Matching results based on AKAZE

图15 ORB对比试验结果Fig.15 Matching results based on ORB

图17 FAST+sift对比试验结果Fig.17 Matching results based on FAST+sift

利用传统方法和本文方法分别进行匹配试验后，为了进一步对匹配结果进行分析，对其进行RANSAC(random sample consensus)提纯[11]并统计相应正确率，结果如表4。需要说明的是，试验中是利用基本矩阵模型进行的RANSAC提纯操作，误匹配点对被全部剔除，但同时一些正确匹配点对也会被当作误匹配点对剔除。由表4可以看出，对于本文试验数据而言，对比试验中的10种传统特征匹配流程未能得到或仅得到较少的匹配点对，而本文提出的方法则能够提出较为丰富且准确率较高的匹配点对，最终匹配提纯结果的正确率在90%以上。这进一步说明本文设计的基于深度卷积神经网络的卫星影像匹配方法的正确性和可行性。

图18 Agast+sift对比试验结果Fig.18 Matching results based on Agast+sift

图19 Harris+sift对比试验结果Fig.19 Matching results based on Harris+sift

图20 Shi-Tomasi+sift对比试验结果Fig.20 Matching results based on Shi-Tomasi+sift

3 结束语

影像匹配是数字摄影测量与计算机视觉中重要的研究课题，如何高效、稳健地进行基于特征的影像匹配是众多学者的研究方向。本文结合深度卷积神经网络思想，从另一个角度对这一经典问题进行了研究，实现了一种面向对象的卫星影像匹配方法。本文设计了一种两通道深度卷积神经网络模型，并在此基础上进行优化，设计提出一种空间尺度卷积层结构，用于解决神经网络训练中输入数据的多尺度问题。在此基础上，设计了基于深度卷积神经网络的卫星影像匹配流程，实现了面向对象的卫星影像匹配。试验表明，本文提出的两通道深度卷积神经网络模型及其优化网络模型，能够较好地进行卫星影像匹配模式的学习，基于深度卷积神经网络的影像匹配能够较好地进行卫星影像间的高效、稳健匹配。

参考文献：

[1] 李德仁. 展望大数据时代的地球空间信息学[J]. 测绘学报, 2016, 45(4): 379-384. DOI: 10.11947/j.AGCS.2016.20160057.

LI Deren. Towards Geo-spatial Information Science in Big Data Era[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 379-384. DOI: 10.11947/j.AGCS.2016.20160057.

[2] 李德仁, 张良培, 夏桂松. 遥感大数据自动分析与数据挖掘[J]. 测绘学报, 2014, 43(12): 1211-1216. DOI: 10.13485/j.cnki.11-2089.2014.0187.

LI Deren, ZHANG Liangpei, XIA Guisong. Automatic Analysis and Mining of Remote Sensing Big Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1211-1216. DOI: 10.13485/j.cnki.11-2089.2014.0187.

[3] 严国萍, 何俊峰. 高斯-拉普拉斯边缘检测算子的扩展研究[J]. 华中科技大学学报(自然科学版), 2006, 34(10): 21-23.

YAN Guoping, HE Junfeng. Extended Laplacian of Gaussian Operator for Edge Detection[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2006, 34(10): 21-23.

[4] 赵万金, 龚声蓉, 刘纯平, 等. 一种自适应的Harris角点检测算法[J]. 计算机工程, 2008, 34(10): 212-214, 217.

ZHAO Wanjin, GONG Shengrong, LIU Chunping, et al. Adaptive Harris Corner Detection Algorithm[J]. Computer Engineering, 2008, 34(10): 212-214, 217.

[5] LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[6] KE Yan, SUKTHANKAR R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors[C]∥ Proceedings of the IEEE Computer Society Computer Vision and Pattern Recognition. Washington, DC: IEEE, 2004: 506-513.

[7] BAY H, TUYTELAARS T, VAN GOOL L. SURF: Speeded up Robust Features[M]∥LEONARDIS A, BISCHOF H, PINZ A. Computer Vision-ECCV 2006. Berlin: Springer, 2006: 404-417.

[8] CALONDER M, LEPETIT V, STRECHA C, et al. BRIEF: Binary Robust Independent Elementary Features[M]∥DANIILIDIS K, MARAGOS P, PARAGIOS N. Computer Vision-ECCV 2010. Berlin: Springer, 2010: 778-792.

[9] CALONDER M, LEPETIT V, OZUYSAL M, et al. BRIEF: Computing a Local Binary Descriptor Very Fast[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1281-1298.

[10] 许允喜, 陈方. 局部图像描述符最新研究进展[J]. 中国图象图形学报, 2015, 20(9): 1133-1150.

XU Yunxi, CHEN Fang. Recent Advances in Local Image Descriptor[J]. Journal of Image and Graphics, 2015, 20(9): 1133-1150.

[11] 董杨, 范大昭, 纪松, 等. 主成分分析的匹配点对提纯方法[J]. 测绘学报, 2017, 46(2): 228-236. DOI: 10.11947/j.AGCS.2017.20160250.

DONG Yang, FAN Dazhao, JI Song, et al. The Purification Method of Matching Points Based on Principal Component Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 228-236. DOI: 10.11947/j.AGCS.2017.20160250.

[12] ŽBONTAR J, LECUN Y. Computing the Stereo Matching Cost with a Convolutional Neural Network[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 1592-1599.

[13] ZAGORUYKO S, KOMODAKIS N. Learning to Compare Image Patches via Convolutional Neural Networks[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 4353-4361.

[14] HAN Xufeng, LEUNG T, JIA Yangqing, et al. MatchNet: Unifying Feature and Metric Learning for Patch-based Matching[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 3279-3286.

[15] PAL S K, MITRA S. Multilayer Perceptron, Fuzzy Sets, and Classification[J]. IEEE Transactions on Neural Networks, 1992, 3(5): 683-697.

[16] TRAPPEY A J C, HSU F C, TRAPPEY C V, et al. Development of a Patent Document Classification and Search Platform Using a Back-propagation Network[J]. Expert Systems with Applications, 2006, 31(4): 755-765.

[17] SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going Deeper with Convolutions[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 1-9.

[18] ŽBONTAR J, LECUN Y. Stereo Matching by Training A Convolutional Neural Network to Compare Image Patches[J]. The Journal of Machine Learning Research, 2016, 17(1): 2287-2318.

[19] COLLOBERT R, KAVUKCUOGLU K, FARABET C. Torch7: A Matlab-like Environment for Machine Learning[C]∥Neural Information Processing Systems Workshop. [s.l]: BigLearn, 2011.

[20] CHEN Tianqi, LI Mu, LI Yutian, et al. MXNet: A Flexible and Efficient Machine Learning Library for Heterogeneous Distributed Systems[R].Nanjin：Neural Information Processing Systems, Workshop on Machine Learning Systems, 2015.

[21] BROWN M, HUA Gang, WINDER S. Discriminative Learning of Local Image Descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(1): 43-57.

[22] 杜玉龙, 李建增, 张岩, 等. 基于深度交叉CNN和免交互GrabCut的显著性检测[J]. 计算机工程与应用, 2017, 53(3): 32-40.

DU Yulong, LI Jianzeng, ZHANG Yan, et al. Saliency Detection Based on Deep Cross CNN and Non-interaction GrabCut[J]. Computer Engineering and Applications, 2017, 53(3): 32-40.

[23] ALCANTARILLA P F, BARTOLI A, DAVISON A J. KAZE Features[M]∥FITZGIBBON A, LAZEBNIK S, PERONA P, et al. Computer Vision-ECCV 2012. Berlin, Heidelberg: Springer, 2012.

[24] ALCANTARILLA P F, NUEVO J, BARTOLI A. Fast Explicit Diffusion for Accelerated Features in Nonlinear Scale Spaces[C]∥Proceedings British Machine Vision Conference 2013. Bristol, UK: British Machine Vision Conference, 2013.

[25] RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: An efficient Alternative to SIFT or SURF[C]∥IEEE International Conference on Computer Vision. Barcelona, Spain: IEEE, 2012.

[26] LEUTENEGGER S, CHLI M, SIEGWART R Y. BRISK: Binary Robust Invariant Scalable Keypoints[C]∥IEEE International Conference on Computer Vision. Barcelona, Spain: IEEE, 2012.

[27] ROSTEN E, DRUMMOND T. Machine Learning for High-Speed Corner Detection[M]∥LEONARDIS A, BISCHOF H, PINZ A. Computer Vision-ECCV 2006. Berlin, Heidelberg: Springer, 2006.

[28] MAIR E, HAGER G D, BURSCHKA D, et al. Adaptive and Generic Corner Detection Based on the Accelerated Segment Test[M]∥DANIILIDIS K, MARAGOS P, PARAGIOS N. Computer Vision-ECCV 2010. Berlin: Springer, 2010.

[29] HARRIS C, STEPHENS M. A Combined Corner and Edge Detector[C]∥Proceedings of the 4th Alvey Vision Conference. Manchester: Springer , 1988: 147-151.

[30] SHI Jianbo, TOMASI. Good Features to Track[C]∥IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Seattle, WA: IEEE, 1994.