管道机器人自动适应机构设计与越障分析

薛耀勇，张继忠，张 磊

（1.青岛大学 机电工程学院，青岛 266071；2.中国海洋大学 工程学院，青岛 266100）

0 引言

在一般工业、核设施、石油天然气、军事装备等领域中，管道作为一种有效的物料输送手段而得到广泛的应用。为提高管道的寿命、防止泄漏等事故的发生，就必须对管道进行有效的检测维护，管道机器人为满足该需要而产生[1]。目前国内外管道机器人的研究成果已经很多，可是在微小管道、特殊管道（如变径管道、带有U型管的管道）进行检测、维修还刚起步，由于该类管道在各个领域的广泛应用，该类机器人极具研究意义[2]。

履带式机器人能够很好地适应管道的变化，有着良好的机动性能[3,4]，在越障、爬行等方面有着比较明显的优势，正成为国内、外相关领域研究的重点[5]。上海交通大学张云伟等人研发了一种利用丝杠螺母进行传动、平行四边形杆系支撑行走轮的进行漏磁检测的管道机器人[6]。曹建树等人采用ADAMS参数化建模与优化设计功能对管道机器人变径机构进行了优化设计，提高了机器人驱动效率、改善了其性能[7]。张建伟等人研制了一种新型可变径管道机器人，能够适应不同管径的管道并进行了控制实现[8]。本文设计了一款具有管径自适应功能的履带式管道机器人，针对机器人在竖直管道内越障状态进行了受力分析，设计了所需自动适应元件圆柱螺旋弹簧，对自动适应机构进行了动力学分析，提高了管道机器人自动适应管径变化的能力和在管道中的越障能力，为以后管道机器人的研究奠定了基础。

1 机器人系统构成

设计了一种具有管径自适应功能的履带式管道机器人，如图1所示。

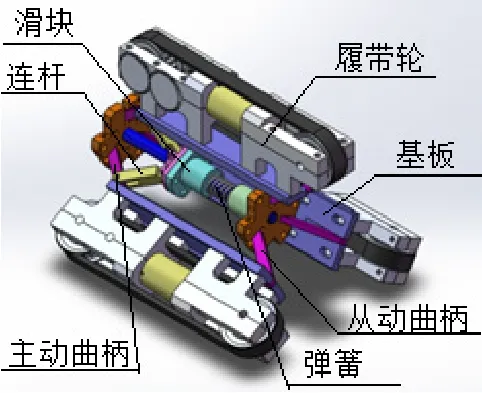
图1 履带式自适应管道机器人

该管道机器人主要包括自动适应装置和履带行走装置。自动适应装置中安装有主动曲柄、从动曲柄、连杆、滑块、圆柱螺旋弹簧等零部件，弹簧元件提供的弹簧力通过滑块推动连杆改变主动曲柄以及从动曲柄的支撑角度使履带轮紧贴管道内壁，履带行走装置为三个履带轮，每个履带轮分别由独立电机驱动行走。该机器人具有良好的越障能力，能自动适应210～220mm范围内不同管径的管道。机器人在管内行走时，履带依靠弹簧力转化而来向外的撑力而紧紧压在管道内壁上，履带将与管道内壁发生相对滑动，产生与机器人行进方向一致的摩擦力，机器人靠这一摩擦力实现在管道内的爬行，而且在垂直管道内爬行时，有足够大的驱动力来克服重力与各种爬行阻力，使机器人履带轮紧贴管道内壁上升或下降。

2 机器人越障受力分析

机器人在圆形管道内竖直向上爬行时，不可避免地会遇到障碍，这对机器人在管道内正常行走造成了一定的影响[9]。为保证所要设计机器人的越障性能，在此将障碍假设为同心垂直台阶[10]。为使机器人能够成功地越过障碍，我们需要对机器人的越障能力进行研究，对其通过同心垂直台阶这一过程进行受力分析。

机器人在管道内爬行的速度较低，所以当机器人通过同心垂直台阶时，我们可以对机器人进行静力学分析，并建立静力学平衡方程求出机器人在跨越同心垂直台阶时的受力与机器人各结构参数以及同心垂直台阶的高度之间的关系，从而确定该管道机器人的越障能力。由于机器人履带轮较长，在跨越同心垂直台阶的实际过程中，各个零部件之间难免会产生相对微小的变化和位移，因此在分析机器人越障过程中的受力时考虑实际越障存在的问题。

如图2所示，当管道机器人前端履带轮刚接触到同心垂直台阶时，管道机器人受到自身的重力G，平行四边形支撑杆系对履带轮的压力FN，管道内壁对履带轮的正压力N1、N2，同心垂直台阶的外边缘对机器人指向履带轮前轮中心方向上的支撑力N3和此处履带运动方向上的摩擦力F3，以及管道内壁和履带之间的摩擦力F1、F2。管道内壁的附着系数为µ。

图2 机器人跨越垂直台阶的临界状态受力分析图

图2中其余参数的含义如下：

L为机器人履带轮前轮和后轮之间的中心距；

r为履带轮半径；

h0为机器人重心至履带轮前后轮中心连线的垂直距离；

hω为同心垂直台阶的高度；

α为F3方向与水平方向的夹角。

根据图2可以列出管道机器人在此临界状态时的静力学平衡方程组(1)：

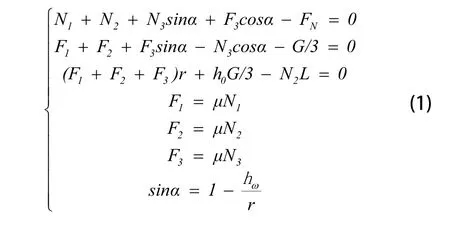
在考虑机器人的自适应机构中的平行四边形支撑杆系发生微小变形这一实际情况下，在机器人前端带轮即将越障的临界状态时的静力学平衡方程组如方程组(1)所示。此时，机器人履带轮前轮并未离开管道内壁，仍受到管道内壁对其的正压力N1、N2，当管道机器人继续向上爬行，使前轮刚好离开管道内壁，而考虑机器人自适应机构中的平行四边形支撑杆系发生微小变形这一实际情况后，管道内壁对履带轮后轮仍然有正压力，则此时管道内壁对机器人的正压力N1=0，此处摩擦力F1=0，将其代入上面的方程组中，则方程组(1)可以简化为方程组(2)：

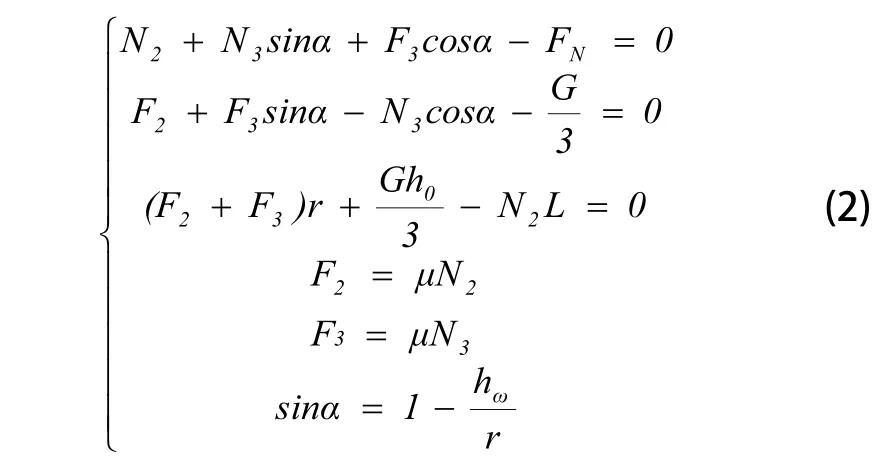
由以上方程组(2)可以得到此状态时：

各力的表达式，如方程组(3)所示：

根据方程组(3)，将机器人的重力G=30N、管道内壁的附着系数μ=0.75、越障同心台阶高度hω=3mm、机器人重心至履带轮前后轮中心连线的垂直距离h0=81.74mm、机器人履带轮前轮和后轮之间的中心距L=174mm、履带轮半径r=23.5mm等参数代入其中即可求出机器人越3mm同心垂直台阶所需要平行四边形支撑杆系对机器人履带轮的正压力FN=52.6N。

经过对机器人越障过程中履带轮的受力分析可知，机器人前端带轮即将越障的临界状态是管道机器人在越障过程中所受阻力最大的极限状态，极限状态下单个履带轮所需自适应机构的平行四边形支撑杆系提供的正压力FN经计算为52.6N，那么整个机器人三个径向均布的履带轮所受前进阻力以及所需要平行四边形支撑杆系提供的正压力都是单个履带轮所受前进阻力以及所需平行四边形支撑杆系提供的正压力的三倍，则通过对管道机器人越障过程中的受力分析，为之后管道机器人自动适应机构弹簧元件的设计奠定了基础。

3 自适应元件螺旋圆柱弹簧设计

3.1 螺旋圆柱弹簧主要参数的设计

根据管道机器人越3mm障碍，得到履带轮对管道内壁压力然后为了安全起见按照运用ADAMS对管道机器人自动适应机构进行静力学分析得到在管径220mm时弹簧为满足管道机器人越障的要求需要提供140N的弹力、在管径210mm时弹簧为满足管道机器人越障的要求需要提供180N的弹力。

根据工作条件，材料选用Ⅲ类碳素弹簧钢丝。通过估取并检验的方法最终得到弹簧中径D2=18mm并确定其许用应力为637.5MPa。根据强度条件计算出弹簧钢丝直径d为2.5mm。根据刚度条件计算出弹簧工作圈数n为9.5圈。

3.2 螺旋圆柱弹簧其他结构参数的计算

根据弹簧在提供140～180N弹力的过程中弹簧的形变量为5.6mm计算出弹簧刚度为Kp=7.0N/m。

根据弹簧刚度计算出弹簧各种状态下所受载荷、弹簧压缩量以及对应的弹簧长度，如表1所示。

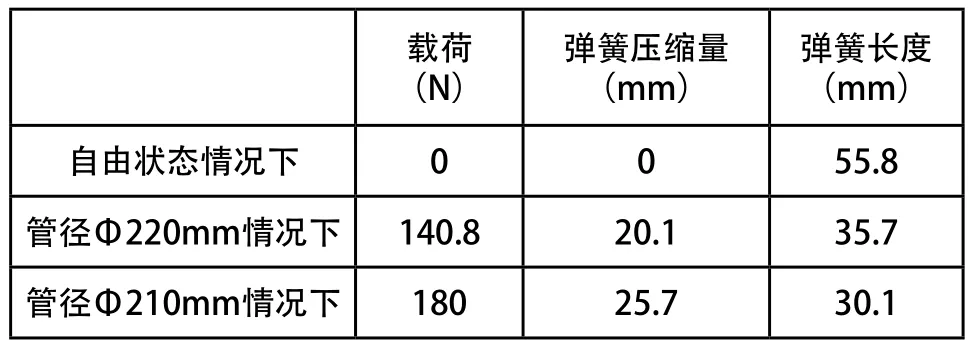
表1 弹簧各状态下压缩量以及弹簧长度

根据所设计的管道机器人结构参数计算得在中心轴上需要加一个25.6mm的套筒，自由状态下弹簧长度为55.8mm，此时弹簧安装长度加上套筒的长度为81.4mm小于机器人结构要求的安装长度97.7mm，因此是符合要求的。

4 自适应机构动力学仿真分析

4.1 创建自动适应机构模型

弹簧在管径220mm到管径210mm变化过程中可以提供的弹簧力为140.8～180N，那么弹簧在管径220mm至管径210mm变化过程中所提供的弹簧力大小可以用下面的函数来表示。

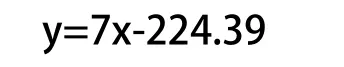
式中x为连杆与中心轴滑块连接板之间的连接点相对于中心轴前支架与主动曲柄之间连接点的横坐标；

y表示弹簧提供的弹力。

利用ADAMS完成了管道机器人自动适应机构仿真模型的创建，如图3所示。

图3 自动适应机构仿真模型

4.2 仿真分析及结果

主动曲柄和连杆之间添加的转动副处合力变化情况，主动曲柄和基板之间添加的转动副处Z轴方向分力变化情况，从动曲柄和基板之间添加的转动副处合力和Z轴方向分力变化情况如图4～图7所示。

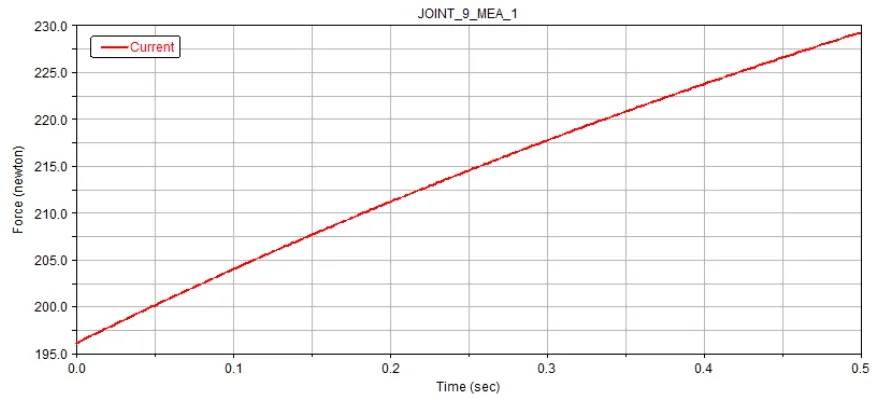
图4 主动曲柄和连杆转动副合力变化

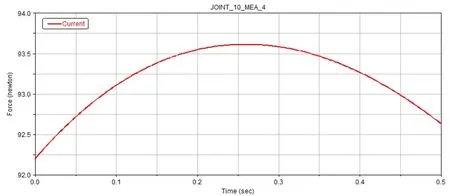
图5 主动曲柄和基板转动副处Z轴方向分力变化

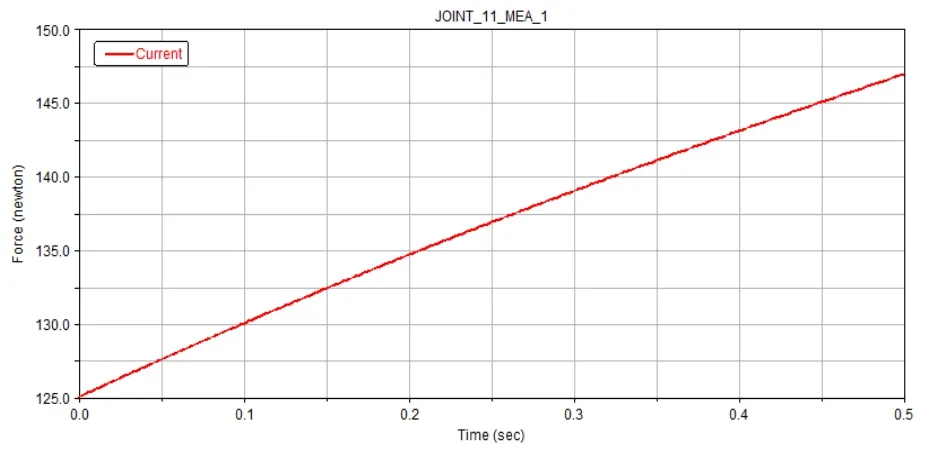
图6 从动曲柄和基板转动副处合力变化

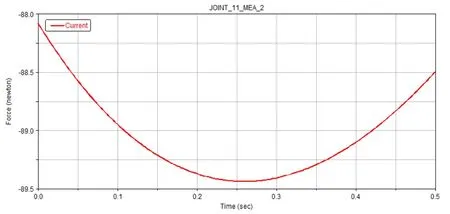
图7 从动曲柄和基板转动副处Z轴方向分力变化

对主动曲柄和基板之间添加的转动副处Z轴方向分力变化情况、从动曲柄和基板之间添加的转动副处Z轴方向分力变化情况进行处理便可以得到所设计的弹簧提供的弹力传递给基板，然后由基板、履带轮这个固定件施加给管道内壁的压力大小为180.3N～183.1N，如图8所示。

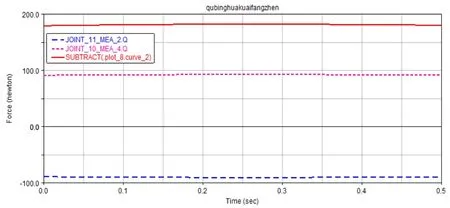
图8 履带轮对管道内壁压力

履带轮实际提供给管道内壁的压力180.3N～183.1N可以满足管道机器人所需要对管道内壁提供的压力157.8N，从而满足管道机器人越3mm障碍的性能要求。而且，经过运用ADAMS对管道机器人自动适应机构进行动力学仿真分析，得到了自动适应机构关键节点的受力情况，为以后关键零部件的有限元分析奠定了基础。

5 结论

设计了一种具有管径自适应功能的履带式管道机器人，对机器人在管道内竖直向上爬行过程中攀越垂直障碍状态进行了受力分析，设计了所需自动适应元件圆柱螺旋弹簧，对自动适应机构进行了动力学分析，经分析得到履带轮实际提供给管道内壁的压力可以满足管道机器人所需要对管道内壁提供的压力157.8N，从而满足管道机器人在竖直管道内向上越3mm障碍的性能要求。

[1]王殿君,李润平,黄光明.管道机器人的研究进展[J].机床与液压,2008,36(4):185-187.

[2]甘小明,徐滨士,董世运,等.管道机器人的发展现状[J].机器人技术与应用,2003(6):5-10.

[3]ShigeoHirose, Hidetaka Ohno,,TakeoM itsui Kiichi Suyama.Design of in-pipe in spection vehicles forφ25,φ50,φ150 pipes[J].IEEE International Conferenceon Robotics and Automation,1999,5:2309-2314.

[4]Dongxiang Chi,GuozhengYan. From wired to wireless a miniature robot for intestinal inspection[J].Journal of Medical Engineering&Technology,2005,27(2):71-79.

[5]赵建伟,杨壘,商德勇,等.薄煤层工作面巡检机器人越障动力学建模与分析[J].制造业自动化,2015,(15):7-9.

[6]张云伟,颜国正,丁国清,等.煤气管道机器人管径适应调整机构分析[J].上海交通大学学报,2005,(6):950-954,959.

[7]曹建树,曹振,徐宝东.基于ADAMS的管道机器人变径机构优化设计[J].制造业自动化,2015(14):1-4.

[8]张建伟,齐咏生,王林.一种新型可变径管道机器人的结构设计与控制实现[J].测控技术,2014,33(10):64-67.

[9]朴春日,颜国正,王志武,等.一种履带式机器人设计及其越障分析[J].现代制造工程,2013,(3):24-27.

[10]庄皓岚,颜国正,王志武,等.多节履带式机器人系统组成和越障性能研究[J].测控技术,2013,32(8):59-62,66.