乌鲁木齐地区风光互补发电系统优化研究

樊小朝，史瑞静，王维庆，李永东

(1.新疆大学电气工程学院，新疆乌鲁木齐830047； 2.清华大学电力系统国家重点实验室，北京100084)

0 引 言

目前新能源发电技术主要有风力发电、太阳能发电、生物质发电等[1-2]。绝大多数地区夏季太阳光照强，但风力较弱；冬季风能资源丰富而太阳能资源较少，利用太阳能与风能在全年不同季节和不同时间的互补性，将风电机组、光伏阵列和蓄电池组成风光互补发电系统，通过智能控制使其满足全年不同时间的用电需求，供电成本将比单独的风力或光伏发电低很多[3- 4]。我国风光互补发电项目迅猛发展，目前大量的风电项目在各地建设并投入运行，2013年12月31日内蒙古满洲里东园风光电站正式投入运行；2016年10月26日江西大唐国际沙岭风光互补项目正式并网发电；2015年9月27日中电投宣化风光互补发电项目一期并网发电；2016年7月27日民勤红沙岗风光互补试验发电项目投产发电。但是，运行效率普遍不高，有待提高[5- 6]。

目前国外在风光互补发电系统的设计时，对于功率的确定方法有两种[7- 8]：一是功率匹配，主要用于系统的优化控制，光伏阵列的功率和风机的功率和大于负载功率；二是能量匹配，主要用于系统功率设计，在光伏阵列的发电量和风机的发电量的和大于等于负载的耗电量。在国内，对风光互补发电系统的优化进行了研究，科学院电工利用遗传算法优化匹配，内蒙古大学新能源研究中心的小型户用风光互补发电系统计算机辅助设计，匹配计算、系统控制等方面进行了研究。

综上，对新疆乌鲁木齐地区风光互补系统研究很少，因此本文基于乌鲁木齐风光数据，利用遗传算法，对风光互补系统进行了优化设计研究。

1 乌鲁木齐地区风能、太阳能情况

根据乌鲁木齐气象观测站近10年的统计，风能功率密度及有关气象参数的部分月均值如表1所示。

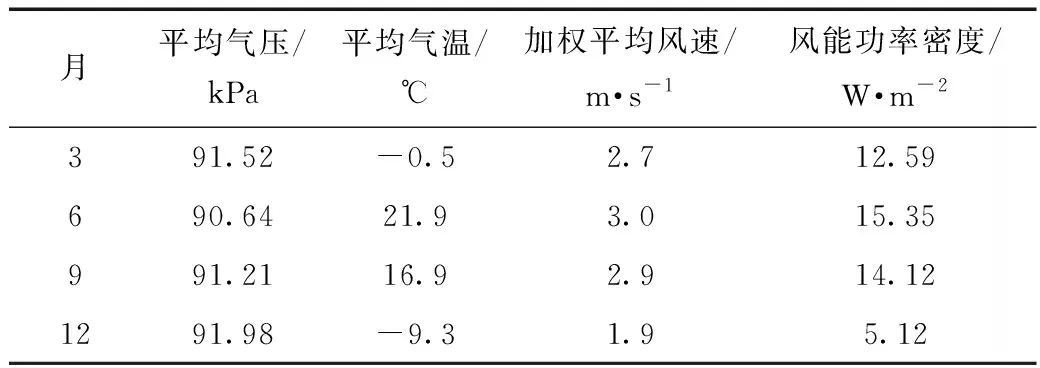
表1 乌鲁木齐地区风能功率密度

本文小型风机正常运行并输出功率的最大风速风机在可利用风速(v1，v2)范围内所输出的能量E

(1)

式中，T为时间；c为韦伯分布的尺度参数；k为韦伯分布的形状参数；Pv为风机输出功率。

该小型风机年累计发电量达到15 000 MJ，风机利用率可以达到0.35以上。

乌鲁木齐具有丰富的太阳能资源，日照时数分布如图1所示，太阳照射时间长，辐射量大可以发展光伏发电。

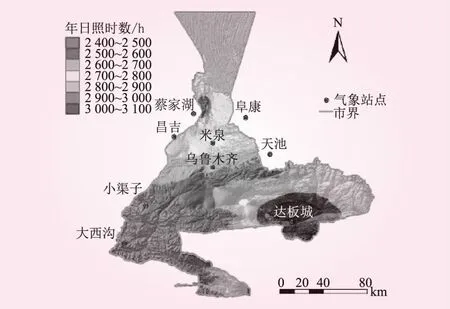
图1 乌鲁木齐年日照时数分布示意

乌鲁木齐辐射量最高的时间出现在6月，最低的时间是12月，光伏阵列倾角取以低于纬度角为宜，以获得在夏季最稳定的输出[7]。

2 风光互补发电系统的设计与优化

2.1 风光互补发电系统设计

风电和光电具有时间互补特点。大多数地方夜晚的风速比白天的大很多风力发电机可以输出较高的风能；而光伏发电则在白天可以获得较高的能量。两者在能量来源上具有很好的互补性，并且两个发电系统可以共用部分蓄能设备和控制器件，所以两者的结合构成一个发电系统很大的优势风光互补发电系统是一种新能源发电系统，其综合利用风能和太阳能资源，具有良好的应用前景。

独立式风光互补发电系统如图2所示，利用光伏阵列，风机发电，然后存储到电池组中，当用户需要电力时逆变器将被存储在电池组的直流电力转换成交流电的能量通过传输线到负载。

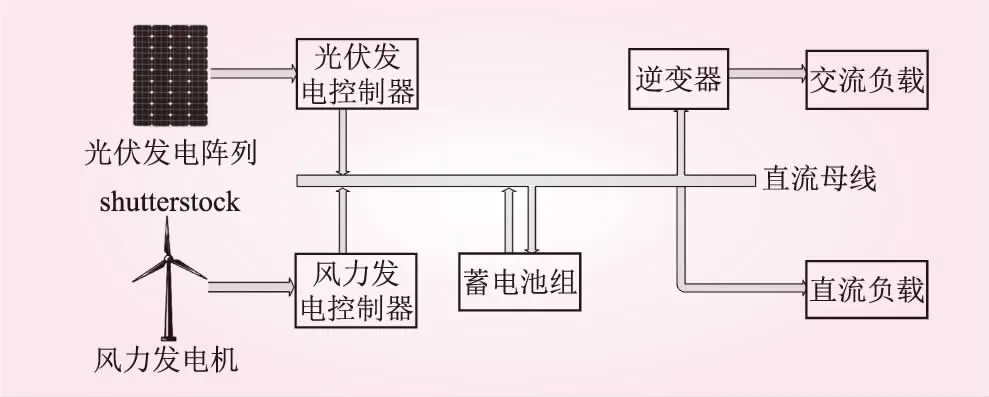
图2 独立式风光互补发电系统的组成

2.2 风光互补发电系统优化设计的数学模型

2.2.1 系统优化的设计变量

风光互补发电系统设计与配置时需要优化的4个变量：风力机数量NW、光伏组件数量NPV、蓄电池组数量Nb、光伏阵列安装倾角s，可表示为

X=[NW，NPV，Nb，s]

(2)

2.2.2 目标函数

风光互补系统总目标是以最低发电成本达到最佳的发电状态，系统成本Call由系统初始安装成本Cins和后期维护成本Cmat两部分组成[7]，即

Call=Cins+Cmat

(3)

系统运行维护成本主要和负载系统总容量及负载大小有关，当负载大小一定时，容量越大，则其运行维护的成本也越高，并且风光互补在设计使用年限内运行维护的成本占相当高比例的是储能元件的更换和风机的保养，这部分发电成本对优化设计模型影响很小，所以在优化设计时暂时不考虑系统的运行维护成本，仅考虑系统初次安装成本。根据系统优化设计目标，即获得最低的初始安装成本，目标函数为[9]

minCins=CWNW+CPVNPV+CbNb

(4)

其中,Cw、CPV、Cb分别为风机、光伏组件以及蓄电池组单价，单位均为元。

2.2.3 约束条件

风光互补发电系统的优化设计需要与负荷需求相匹配，系统需要满足负载，在一定时间内可靠运行前提下，达到成本降到最低的目标[9]。

设定评估期为一年，以天为时间间隔时间段，风机、光伏发电量EW、EPV分别为

EW=NWf(VW，PW)

(5)

EPV=NPVf(H，λ，s，n，S，T，PPV)

(6)

式中，VW为风速；PW为风机功率特性参数;式(6)表示光伏阵列发电量EPV与水平面辐射量H、纬度角λ、光伏阵列倾角s、天数n、日照时数S、温度T以及光伏组件功率特性参数PPV和组件的配置数量NPV之间关系。

蓄电池组每天初始容量可以由式(7)与式(8)计算，式中Eb为储能元件的剩余电量；Ebm为最大可用电量；EL为负载耗电量；Eov为盈余电量。即

(7)

Eov(n)=EW(n)+EPV(n)-EL(n)

(8)

忽略外界环境对蓄电池组性能的影响，并将蓄电池组的充放电效率设为1，最大放电深度设定为最大蓄电量的1/2，目的是延长蓄电池组使用寿命。设定设定蓄电池电量初始电量为

(9)

式中,Ebat为储能元件的额定容量。

在时间序列的计算过程中，如果负载缺电则盈余电量Eov显示为负值，负载缺电次数加1。将评估期内负载缺电的次数和除以365天，便得到负载缺电率LPSP，于是系统优化设计的约束条件可以表示为式(10)，式中LPSPset为设定的负载缺电率阈值；光伏阵列的固定倾角s的边界约束为(11)。

LPSP-LPSPset≤0

(10)

0°≤s≤λ+30°

(11)

3 风光互补发电系统优化计算结果与分析

乌鲁木齐气象站气象记录数据累年日平均值进行系统优化设计。负载耗电量采用每日每户5 kW·h，并设定2户和10户两种情况。选择一款额定功率为1 kW的风力发电机，单价为3 500元。光伏电池组件为PVM-50的单晶硅太阳能电池组件，其峰值功率为50 W，单价330元。储能元件容量为12 V，120 A·h的胶体免维护蓄电池，单价1 200元。

利用遗传算法解决具有复杂非线性约束和整数约束的风光互补系统的最优模型。遗传算法迭代计算过程如图3所示。在迭代计算过程中，遗传算法使用惩罚函数法来处理系统优化数学模型中的非线性不等式约束和整数约束。给出了优化过程中历代群体的最优惩罚函数值和平均罚函数值的变化情况。这里将每一代个体数量限定在20，最大遗传代数限定在100，经过50～60代优化选择后就成功收敛，获得了最优解。

图3 风光互补发电系统优化设计的遗传迭代过程

3.1 负载情况下的系统优化

本部分假定了两种负载情况：2户和10户且每户日用电量为5 kW·h。计算结果如表2所示。

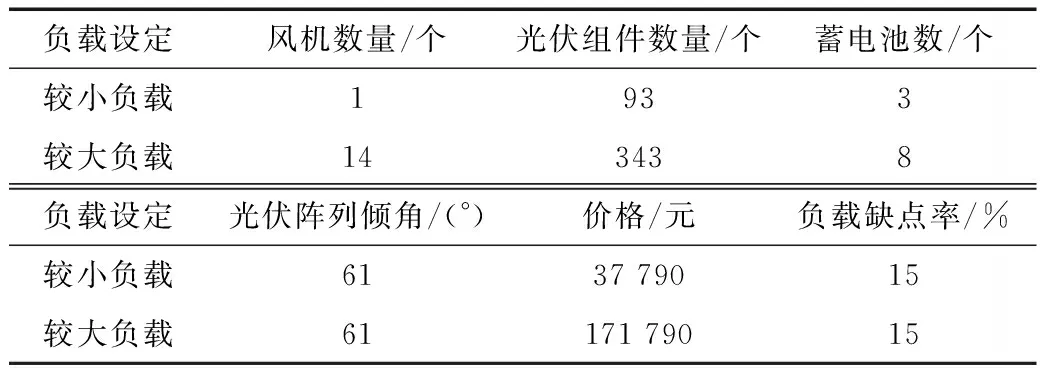
表2 计算结果

3.2 系统仿真运行与技术经济分析

3.2.1 系统仿真运行与分析

将较小负载情况的结果代入能量输出模型，仿真得到风力发电和光伏发电能量输出，如图4所示，蓄电池能量状态和电量盈余状况如图5所示。

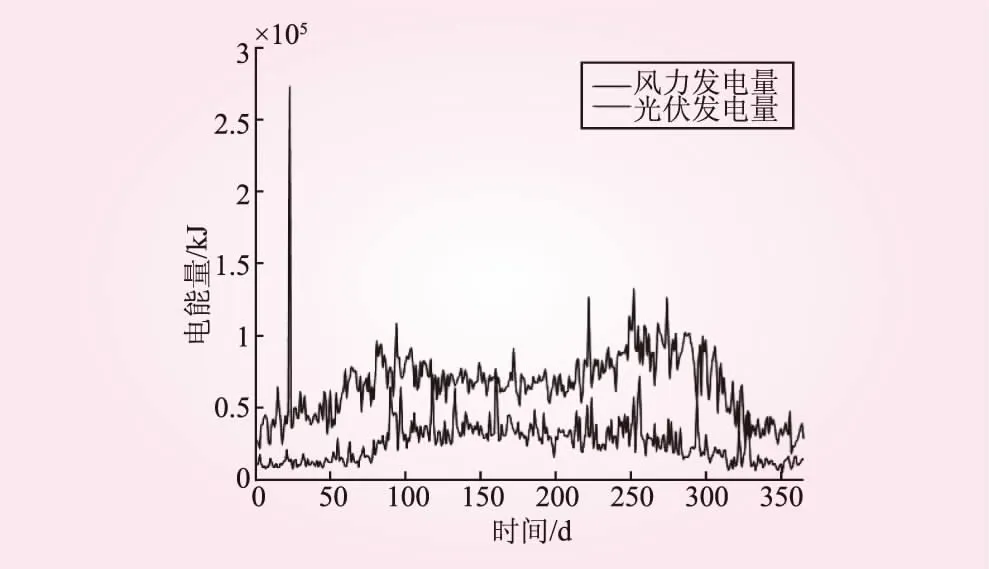
图4 较小负载风力发电和光伏发电能量输出

图5 较小负载蓄电池能量状态和电量盈余状况

将较大负载情况的结果代入能量输出模型，仿真得到风力发电和光伏发电能量输出，如图6所示，蓄电池能量状态和电量盈余状况如图7所示。

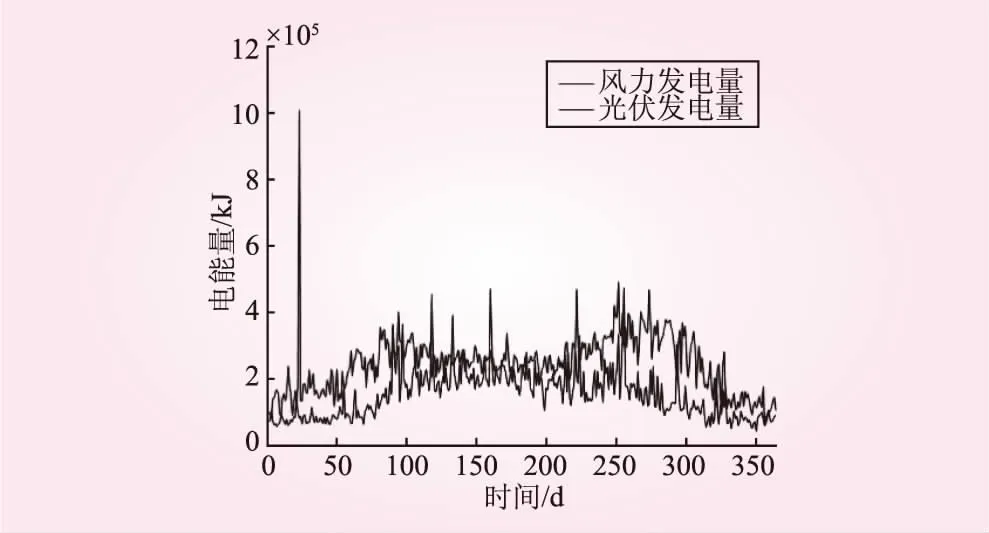
图6 较大负载风力发电和光伏发电能量输出

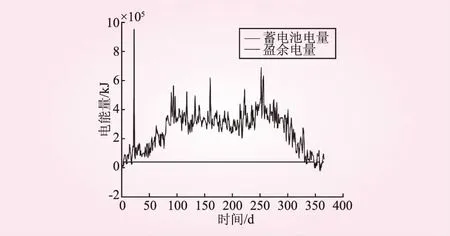
图7 较大负载蓄电池能量状态和电量盈余状况

综上，风力发电量及光伏发电量都极不稳定。大多数时候的时间的发电量都远远超过了负载需要，有大量的输出盈余，部分时间出现盈余电量小于零情况，有缺电情况发生。

3.2.2 系统技术经济分析

经过市场调研，风光互补发电系统各个部件选取要经济性与实用性，经计算得到系统安装成本，如表3所示。其中维护成本为市场调研后估算值，总成本等于初始成本与维护成本之和。供电成本等于总成本除以设备使用年限内总用电量，单位为元/kW·h。

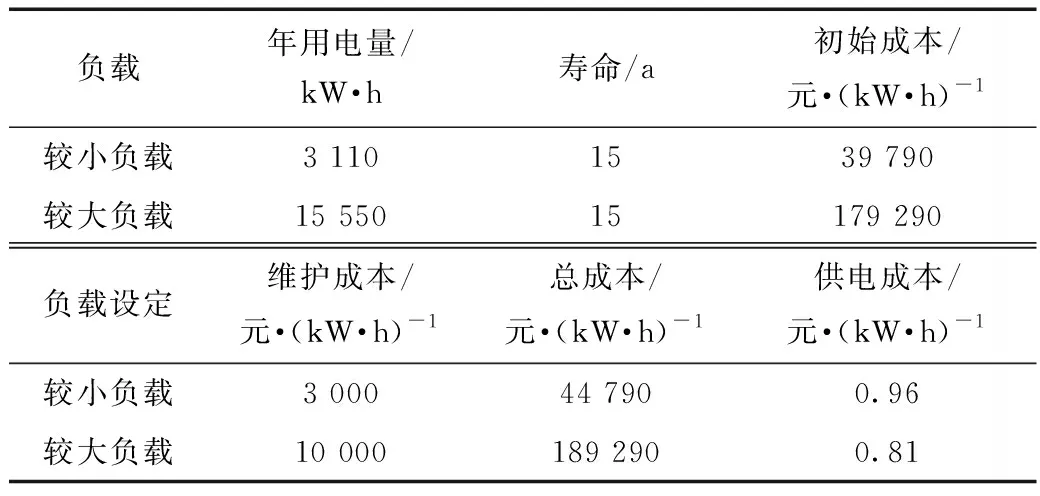
表3 安装成本

计算结果表明风光互补发电系统的供电成本相对于目前的网电价格是偏高的。乌鲁木齐虽然拥有较为丰富风能和光辐射能资源，但季节性差异较大，为了提高供电稳定性使得供电成本也相对较高。针对不同负载容量相比较，适合大负载要求的配置供电成本也会有所降低，当然这也与风机、光伏器件外其他部件选型有关，供电成本存在一定偏差。

4 结论与展望

本文构建了风光互补发电系统，得出了优化设计所必须的目标和约束条件，搭建了风光互补发电系统优化设计数学模型；约束条件为负载缺电率指标，采用时间序列法计算负载缺电率，并搭建风力发电和光伏发电能量输出模型及混合输出模型；然后利用带有惩罚函数的遗传算法对模型进行求解；最后对不同大小的负载情况下，进行系统优化设计并得出结果，结果代入能量输出模型进行分析和仿真运行，根据仿真结果对不同条件下的系统供电成本进行了分析比较。

通过仿真结果发现，风力发电量及光伏发电量都极不稳定。大多数时候的时间的发电量都远远超过了负载需要，有大量的输出盈余，但仍有部分时间发生负载缺电。优化得到的风光互补发电系统可以满足对电能质量要求不高的用户，建议发展风光互补发电与其他形式相结合的供电模式，对用电量不高或远离供电线的用户可以发展风光柴油发电的用电模式，其他用户可以发展风光-电网非并网形式用电模式。通过经济性计算发现，优化设计得到的发电系统发电成本高于目前电网价格。本文研究将促进新疆新能源的健康可持续发展。

由于乌鲁木齐气象环境季节性差异较大，在冬季为了提高供电稳定性使得供电成本也相对较高，同时为满足冬季供电需求，导致设备投入较高，在其它季节会有大量的电量剩余。因此，风光储设备的优化投入运行将是下一步研究重点。

[1] 史瑞静, 李凤婷, 樊小朝, 等. 风电场风电利用水平综合评价指标体系的研究分析[J]. 水力发电, 2015(3): 80- 83．

[2] 李明, 胡殿刚, 周有学. 基于“两个替代”战略的甘肃新能源就地消纳模式研究与实践[J]. 电网技术, 2016, 40(10): 2991- 2997．

[3] 李成, 杨秀, 何海国, 等. 基于风光互补的独立微网系统容量优化[J]. 电源技术, 2016, 40(3): 610- 613．

[4] 刘锡文, 赵河立, 闫玉莲, 等. 风光互补海水淡化系统的技术经济分析[J]. 水处理技术, 2016(6): 127- 130．

[5] 许童羽, 王亮, 陈春玲, 等. 户用风光互补发电系统电能质量研究[J]. 沈阳农业大学学报, 2015, 46(4): 502- 507．

[6] 董军, 冯天天. 基于物元—可拓的大型风光互补发电项目后评价方法[J]. 水电能源科学, 2015(4): 206- 210．

[7] 赵昕宇. 风光互补发电潜力分析与系统优化设计研究[D]. 郑州: 河南农业大学, 2014．

[8] 叶承晋, 黄民翔, 王焱, 等. 基于离散概率模型的风光互补供电系统优化配置[J]. 电力系统自动化, 2013, 37(6): 48- 54．

[9] 崔勇, 杨菊芳, 张栋. 基于风光互补的主动电网规划模型[J]. 中国电力, 2017, 50(5): 101- 106．