弧形闸门支臂结构的非线性振动及混沌现象

张 健，谢智雄

(河海大学机电工程学院，江苏常州213022)

0 引 言

弧形闸门支臂结构的安全影响着整个弧形闸门的安全，根据国内外对弧形闸门事故的调查分析发现：弧形闸门产生破坏的主要原因就是闸门支臂结构的失稳破坏，并且有文献指出，只要动水压力的激振能量不是很大，闸门不容易出现整体框架结构的振动，但是支臂发生单独振动的可能性却是很大的，因而有必要对弧形闸门支臂结构的非线性振动做进一步的分析研究。

混沌来源于非线性，在非线性振动过程中有可能存在混沌现象，在线性系统中不会产生。混沌存在于某些确定性的系统中，而且不需要任何附加的随机因素。混沌振动具有以下的一些特点：由确定性因素产生，具有有界性，具有非周期性，对初始条件具有极端敏感性。本文通过有界性和非周期性来判断弧形闸门支臂结构振动是否存在混沌现象，并通过功率谱图和Lyapunov指数进一步确认了支臂结构振动确实存在混沌现象。

1 闸门支臂结构动力微分方程的建立

根据文献[1]，在一定开度下，弧形闸门泄流产生的动力荷载可以转化为周期性变化的动水荷载，在考虑到考虑非线性影响因素后，其动力屈曲方程的一般形式为

(1)

式中，A，B，C是与梁的动力屈曲模态有关的常数矩阵；I为单位阵；f为广义坐标列阵；Φ(t)为周期函数；α、β为荷载参数。

方程(1)是一个齐次非线性微分方程，而混沌只会发生在非线性系统中，因而研究方程(1)是有可能发现混沌现象的。

1.1 支臂结构的计算简图

根据国内外一些实测结果，将支臂结构按照两端铰接压杆计算得到的自振频率值与实测频率值很接近，因此可以将支臂结构按照简支梁模型来分析。本文将支臂看成是两端铰接的压杆，在轴向干扰力的作用下进行动力稳定性分析，支臂结构的计算模型如图1所示。

图1 支臂结构计算模型

1.2 支臂结构动力学微分方程的建立

对于图1所示的支臂结构的计算模型，在荷载的作用下支臂将产生横向弯曲，根据文献[3]发现支臂阻尼对支臂振动主要不稳定区域的影响较小，可忽略阻尼对支臂振动的影响。

根据支臂结构的计算模型，由动力平衡条件，建立无阻尼动力微分方程为

(2)

式中，E为弹性模量；I为截面惯性矩；p0+ptcos(θt)为周期性变化动水荷载；A为支臂横截面面积；α为支臂的倾角；m为支臂的质量；v为支臂的挠度。

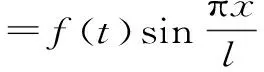
(3)

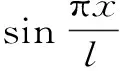
由式(3)可得

(4)

(5)

于是可得到无量纲形式的动力学微分方程

(6)

2 支臂结构振动的混沌现象

混沌是发生在确定性非线性系统中的貌似随机的无规则运动，看似混乱无序，但是又颇有规律。由于系统的非线性，在满足一定条件的振动系统中，即使是在受到规则的激励后也会产生貌似无规则的永不重复的振动响应。混沌产生的主要原因就是系统对初始条件的十分敏感性，即使初始条件有微小的差别也有可能使得系统产生混沌现象。混沌运动的形态是十分复杂的，很难通过解析计算来描述，本文主要是通过计算机的数值仿真来实现对混沌现象的描述。

弧形闸门在发生振动时，支臂会产生动力不稳定区域，当非线性振动系统不稳定时，就有可能产生混沌现象，因此在研究混沌振动之前，要先解决系统振动稳定性问题。根据一些调查弧形闸门失事报告经过解析分析得出结论：在把支臂作为两端铰接的轴心压杆，所施加的轴向干扰力为p(t)，当干扰力的频率θ等于支臂的横向振动固有频率Ω的2倍时，支臂将发生参数共振，丧失稳定。在本文中分析混沌振动时不妨取θ=2Ω，此时当施加的轴向干扰力的某些参数发生改变时，系统就有可能会发生混沌现象。

(7)

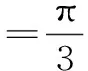
将以上数据整理后代入一阶微分方程组(7)，采用MATLAB程序利用四阶龙格库塔方法进行数值分析，绘制相图、时程曲线图、功率谱图并计算Lyapunov指数，通过这些方法进行混沌的数值识别，当图像满足一定的条件时，即可判定该系统是否出现了混沌现象。混沌的相图不是单独的一条封闭的曲线，而是一个具有往复性并且局限在某一区域内的图形；混沌运动是非周期性运动，功率谱谱线是类似于噪声的连续谱线，但是利用功率谱图还是很难区分真正的混沌运动和随机运动的；而Lyapunov指数就能避免这个问题，只要当Lyapunov指数中有一个值是正值，此时就产生了混沌运动。

在实际工程中，脉动压力幅值(即pt)是一个变量，因此在本文中以c为变量，通过选择不同的值，利用程序绘制出相应的图像。

取c=5，相图和时程曲线如图2、3所示。

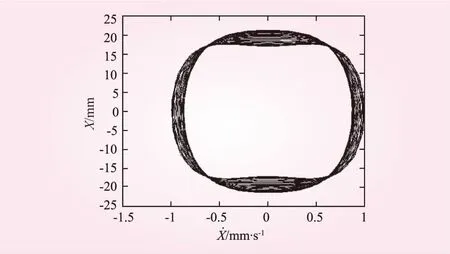
图2 相图

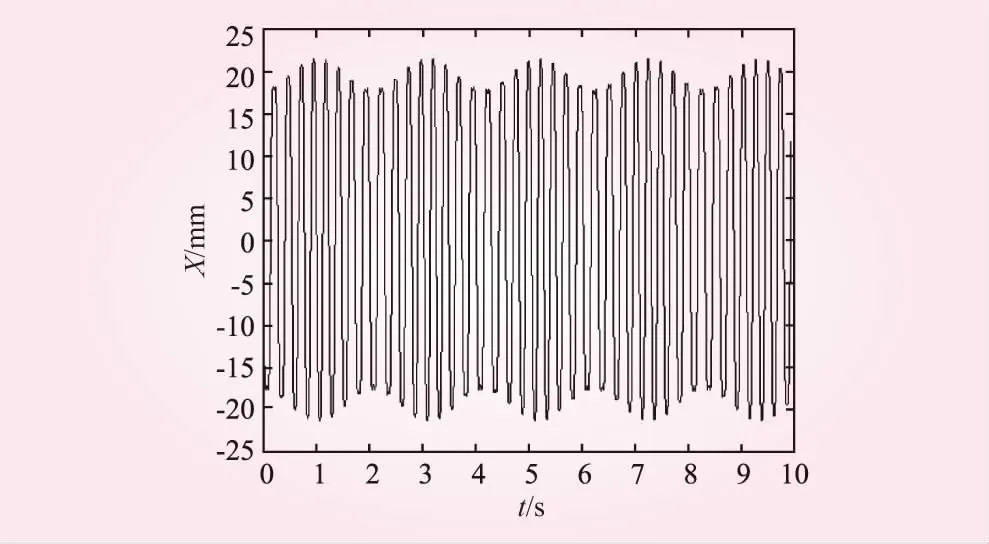
图3 时程曲线

显然，相图是一个环面，时程曲线图是一个规则的周期图像，因而这是一个周期运动。此时弧形闸门支臂没有产生混沌现象。

取c=14，相图和时程曲线如图4、5所示。

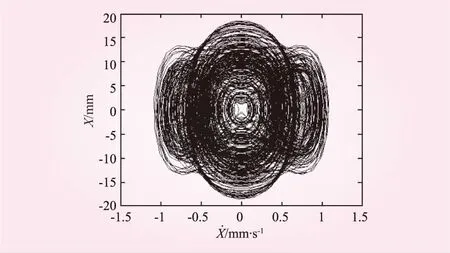
图4 相图

图5 时程曲线

显然，相图是局限在一定区域内的不重复图像，时程曲线图是一个类似噪声无规律谱线图，因而在此时系统有可能出现了混沌现象。

取c=14.8，相图、时程曲线图如图6、7所示。

图6 相图

图7 时程曲线

显然，相图是局限在某一区域内永不重复的图像，时程曲线图是一种类似于噪声的无规律谱线，因而可以判断系统有可能存在混沌现象。

为验证此时系统的确存在混沌现象，绘制功率谱图和计算Lyapunov指数如图8、9所示。

图8 功率谱

图9 Lyapunov指数

功率谱图是一种类似于噪声的无规律连续谱线，因而可判断系统有可能存在混沌现象。

3 结 语

利用MATLAB程序数值模拟的方法，通过计算机绘制出的相图、时程曲线图、功率谱图以及Lyapunov指数发现弧形闸门支臂结构在动水荷载的激励下可能会产生混沌现象。在本文中，周期倍化是产生混沌的途径，当c较小的时候，支臂结构在激励下做周期振动，随着c数值的增大，支臂非线性振动系统中产生了混沌。通过数值模拟的方法发现了混沌产生的途径，对弧形闸门支臂结构的混沌振动有了更加直观的认识。

[1] 朱召全, 卓家寿, 陶桂兰. 弧形闸门的动力稳定性研究进展[J]. 水利水电科技进展, 1999, 19(5): 27- 29．

[2] 谌磊. 弧形钢闸门空间框架的动力稳定性分析[D]. 西安: 西农林科技大学, 2006．

[3] 李火坤, 练继建. 偏心荷载作用下弧形闸门支臂的动力稳定性研究[J]. 南昌大学学报, 2006, 28(1): 72- 77．

[4] 龙运佳. 混沌振动研究方法与实践[M]. 北京: 清华大学出版社, 1996．

[5] 王聪玲, 龙运佳. 关于混沌振动的研究[J]. 中国农业大学学报, 1997, 2(6): 23- 27．

[6] 陕振沛, 宁宝权, 张转周. 基于MATLAB的各类混沌系统的计算机仿真模拟研究[J]. 科技广场, 2015, 6(1): 6- 11．

[7] 张静. 混沌系统的计算机仿真[J]. 实验室研究与探索, 2008, 27(8): 58- 59．

[8] 赵弘, 张登山. 混沌振动研究[J]. 钢铁研究, 2003, 134(5): 36- 40．

[9] 何四祥, 邹祖军. 混沌运动在一类非线性结构振动中的数值模拟研究[J]. 结构工程师, 2007, 23(1): 42- 44．

[10] 李娜, 赵凤群, 王苗苗. 非保守简支梁的非线性振动与混沌现象[J]. 陕西科技大学学报, 2011, 29(6): 56- 59．