基于DEM法氢气直接还原竖炉内物料运动行为研究

刘 栋, 龙 鹄, 白明华, 葛俊礼, 徐 宽

(1. 宝武集团广东韶关钢铁有限公司，广东 韶关 512123; 2. 燕山大学 国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛 066004; 3. 河北港口集团港口机械有限公司，河北 秦皇岛 066004)

0 前言

由化石燃料燃烧产生的温室气体导致的气候变暖现象已成为全球共同面对的问题，钢铁行业是工业当中的温室气体排放大户。据统计[1,2]钢铁厂的吨钢CO2排放量约为1 832 kg，其中高炉炼铁占全流程的76.1%。同时高炉由于大量使用焦炭以及烧结矿，是SO2、NOx、粉尘的主要来源[1,2]。以碳还原铁矿石为高炉技术核心的传统长流程钢铁工业亟待转型发展[3]。

氢气(H2)作为还原剂在竖炉内生产直接还原铁，可降低炼铁过程中的碳耗并减少CO2排放。该还原过程在低于铁矿石软化温度下进行，因此氢气还原竖炉是一种典型的气固逆流式移动床[4-6]。物料在竖炉内下降过程中的运动行为直接影响炉内流场分布，与炉况的稳定性和生产率息息相关。当固态物料呈平推流的状态均匀向下移动时，可使得物料在炉内停留时间一致，即得到较为均匀的还原，有利于操作稳定性。否则，当运动速率沿径向分布不均，会导致部分物料未得到有效还原，从而降低生产效率[7,8]。前期通过实验研究已知氢气还原速率较快[9,10]，从反应速率角度考虑，其还原段高度与传统竖炉相比可有效降低，但从炉内物料运动均匀性考虑，高度的降低可能会带来新的问题。

本文通过离散单元法(DEM)建立竖炉内炉料颗粒运动模型，针对不同高度条件下炉内物料运动情况进行分析，对比氢气竖炉与传统Midrex竖炉内物料沿径向速率分布的差别，为氢气直接还原竖炉炉型及设备设计优化提供理论指导。

1 竖炉及排料机参数

传统Midrex及HYL直接还原竖炉主体部分通常由还原段、过渡段、冷却段三段构成，炉料自竖炉顶部的料斗、炉料分配器进入还原段，在还原段内下降，与逆流的还原气之间发生反应，完成从氧化铁矿石到海绵铁之间的转变。冷却段下方由摆式或轮式卸料机负责卸料。Corex熔融炼铁法是通过竖炉底部的螺旋排料机将还原得到的热态海绵铁排出竖炉，并由螺旋机下方的下降管进入下部的熔融气化炉。

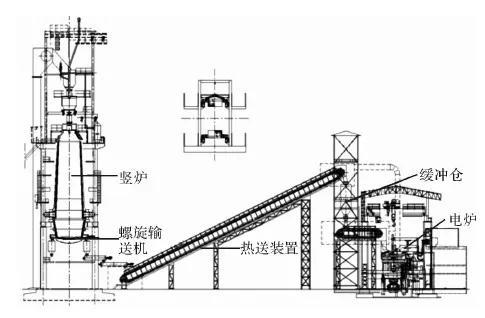
图1 直接还原铁热送至电炉示意图

传统竖炉冷却段较高，为了减少能耗，并有效降低竖炉整体高度，本文研究采用热送工艺，即通过热螺旋输送机进行竖炉内直接还原铁排料，然后热送至电炉炼钢厂，流程如图1所示，并通过调整螺旋机叶片直径、轴径，齿数等方法调节炉内物料运动情况。

1.1 炉主要参数

Siderca厂[11]的海绵铁产量为100 t·h-1，年产量约为80万吨，竖炉还原段直径为4.88 m，高度为10 m，高径比约为2，有效容积和还原段利用系数按式(1)、(2)计算得到，分别为186.9 m3和11.9 t·m-3·d-1。当产能一定时，还原段利用系数与有效容积呈反比关系。氢气还原效率高，还原段利用效率相应增大，在竖炉直径保持不变的条件下，高度可减小。本文研究的氢气竖炉直径参照Siderca数据，取5 m，高度有所减小，分别为8 m，6 m，与Midrex竖炉直径为5 m，高度为10 m情况进行对比。为简化模拟未考虑炉壁倾角。

Veff=0.785D2·H

(1)

ηeff=24QS/Veff

(2)

式中，Veff是还原段有效容积，m3；D是还原段直径，m；H是还原段高度，m；ηeff是还原段利用系数，t·m-3·d-1；QS是每小时海绵铁产量，t·h-1。

1.2 螺旋输送机参数计算

直接还原竖炉中的螺旋输送机用于热海绵铁的卸料，该设备对调节炉内物料运动行为，控制均匀的下降流流型具有重要的作用，并进一步影响到炉内气流分布以及操作的稳定性。

螺旋输送机的关键参数主要包括叶片直径、螺距、以及螺旋叶片升角，通过公式[12,13]对螺旋机关键参数进行计算。

螺旋直径D为

(3)

式中，D为螺旋直径，m；K为物料综合系数；Q为输送量，t·h-1；φ为充满系数；γ为物料的堆比重，t·m-3；c为倾角系数。

螺旋输送机螺距、螺旋轴直径以及螺旋叶片的升角分别由式(4)～(6)计算得到。

S=bD

(4)

d=(0.2～0.35)D

(5)

α=arctan(S/2πr)

(6)

式中，S为螺距，m；b为螺距/螺旋直径系数；R为螺旋轴的半径，m。

本次研究一共设8台螺旋输送机，沿竖炉底部径向均匀分布。计算得到基本模型条件下螺旋排料装置叶片尺寸参数见表1。

表1 基本模型螺旋排料装置叶片尺寸参数

2 DEM模型的建立

离散元法( Discrete Element Method)是将整个研究区域离散为多个独立的运动单元，且每个单元具有一定几何特征(包括形状、大小、排列等)和物理特性以及化学特性[14, 15]。各单元运动过程受经典运动方程控制。本次研究利用EDEM软件，采用离散单元法建立数值模型，对氢气还原竖炉内炉料的运动行为进行仿真模拟，分析料型分布，研究固态物料运动特性，并与传统Midrex竖炉进行对比。

2.1 模拟方法

为了能够描述颗粒间的接触，DEM运用振动运动方程来模拟。颗粒之间沿法线、切线方向的接触力采用“弹簧-阻尼器-摩擦板”的Voigt弹簧阻尼模型来计算，如图2所示。

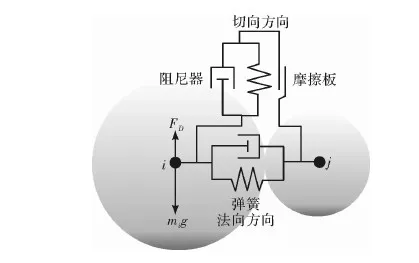
图2 振动接触模型

假设两个球形颗粒之间发生线弹性接触，二者有重叠发生，此时单元体之间由于接触变形所产生的法向力Fn以及切向力Ft的计算如式(7)和(8)所示[14]。

(7)

Ftij=min{μ|Fn,ij|tij,[Kt[Δut,ij+Δφij]+

(8)

式中，K是颗粒的弹性系数；η是颗粒的阻尼系数；μ是颗粒的滑动摩擦系数；Δu是颗粒运动过程中的线位移；Δφ是颗粒运动过程中的角位移；nij是颗粒i到颗粒j的法向矢量；tij是颗粒i到颗粒j的切向矢量。

进行数值求解时采用中心差分法，更新速度用两次迭代时间步长的中间点来表达并计算位移关系，从而得到进一步的作用力。进行时间t内的k次循环计算求解，即可计算得在时间t内任意时间点的任意颗粒的运动。

2.2 颗粒模型的建立

离散元法模拟计算时颗粒数目受到工作站能力限制，而实际生产过程中颗粒数为千万级，为此在建立颗粒模型过程中采用颗粒粒径放大的处理方法，减少模拟时的颗粒数量，降低计算量，并对有关问题及规律做定性分析，这种放大粒径的方法的适用性及准确度在多篇文献中得到了验证[14-16]。

颗粒参数如表2所示，颗粒密度取球团密度，颗粒粒径放大了10倍。

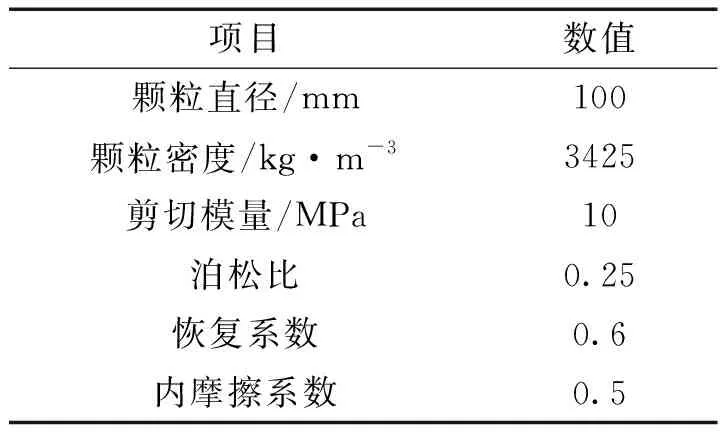
表2 颗粒参数

与炉料颗粒接触的炉壁参数如表3所示。

表3 竖炉炉壁材料参数

螺旋排料装置叶片材料参数如表4所示。

表4 螺旋排料装置叶片材料参数

2.3 物理模型的建立及仿真

氢气竖炉还原段物料运动离散元仿真过程步骤如下：首先利用solidwrks软件建立竖炉及螺旋输送机三维模型；其次，将几何模型导入EDEM软件，并设定所有模拟所需计算参数；然后开始填充物料，当竖炉内物料填充率达到90%时，使螺旋输送机旋转，并将竖炉内物料排出；当物料不再排出时停止模拟计算，收集计算结果数据 并加以分析。

使用Solidworks三维建模软件建立竖炉炉体的离散单元法仿真模型，包括竖炉本体和八台螺旋排料装置，如图3所示。竖炉内径为5 m，还原段高度为10 m，炉壁未设倾斜角。

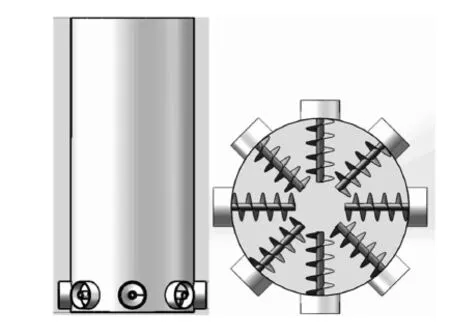
图3 竖炉离散元模拟计算物理模型

3 竖炉内物料运动模拟结果

3.1 基础模型模拟结果

图4所示为基础模型在竖炉不同高度下，水平横截面物料运动速度分布云图，深色表示较快的速率，负值表示与Z轴方向相反。观察可知高度为2 m处，中心速率较快，由中心向四周速率沿径向逐渐减小，中心处物料下降速率最快。物料下降速率沿圆周方向均匀分布，因此纵截面不同高度下的物料下降速率分布可衡量整个竖炉物料运动分布情况。

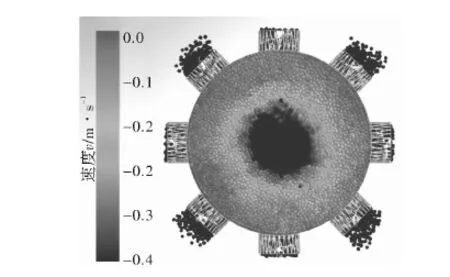
图4 竖炉高度2 m处横截面物料运动速度分布

图5所示为基础模型纵截面物料运动速度分布云图，料层总高度为10 m，观察可知在竖炉高度1/4处，及2.5 m处上方，物料运动速率分布较为均匀，而在2.5 m处下方，出现了下降速率分布不均的现象，中心处速率最大，中心与边缘相比，不受到来自炉壁的摩擦力，且在下方中心处叶片直接将物料旋转输出，因此物料下降速率快。越靠近竖炉上方，或靠近炉壁端，物料下降速率越小。

图5 竖炉纵截面物料运动速度分布

为了量化分析速率变化情况，分别取竖炉高度1 m、2 m、3 m处，厚度为0.5 m的物料沿径向速率分布，如图6～8所示。观察可知，不同高度下的物料下降速率均沿中心向炉壁方向逐渐减小，其中高度为1 m处速率差别最大，为0.34 m·s-1，高度3 m处速率差值较小，为0.1 m·s-1。说明炉料位置越低，沿径向速率分布越不均匀。竖炉靠近中心处(r/R=0.1)，炉料不同高度下的速率分别为0.38 m·s-1(H=1 m)，0.32 m·s-1(H=2 m)，0.28 m·s-1(H=3 m)，高度为1 m处的物料下降运动速率与3 m处的相比增大了35.7%；而靠近炉壁处 (r/R=0.7)，炉料不同高度下的速率分别为0.14 m·s-1(H=1 m)，0.18 m·s-1(H=2 m)，0.22 m·s-1(H=3 m)，高度为1 m处的速率与3 m处的相比减小了36.3%。

通过对基础模型物料速率分布分析可知，当模拟竖炉高度为10 m，直径为5 m(传统Midrex竖炉还原段)时，2.5 m以上物料速率分布沿径向较为均匀，2.5 m以下速率分布不均，中心速率较高，靠近炉壁处速率较低。

通过之前分析，氢气还原速率快，较传统Midrex竖炉，氢气竖炉的还原段可进一步降低，因此本节研究了竖炉高度的减小对炉内物料运动的影响，分别对直径为5 m，炉内物料总高度分别为10 m、8 m、6 m条件下的炉料运动行为进行仿真。

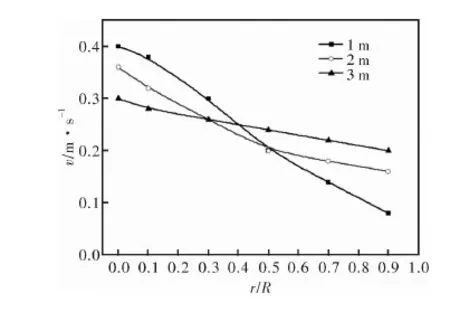
图6 竖炉纵截面物料运动速率分布

3.2 竖炉高度的影响

图7所示为不同料层总高条件下纵截面物料运动速度分布云图，观察可知当料层总高度从10 m降低到8 m时，物料运动速率分布与基本模型基本相近，上层较为均匀，下层不均匀度略有增高，中心深色区域高度略有增加，从2.5 m增大到2.8 m，占总高度比例从25%增大到35%。当总高度进一步降低到6 m时，中心深色区域显著增大，高度约为3.8 m，占据总料层高度的63.3%。

图7 纵截面物料运动速度分布

为了量化分析高度为6 m的还原竖炉物料运动速率变化情况，与基本模型一样，分别取竖炉高度1 m、2 m、3 m处，厚度为0.5 m的物料沿径向速率分布，如图8所示。高度为1 m处速率差别最大，为0.38 m·s-1，高度3 m处速率差值仍较高，为0.33 m·s-1。竖炉靠近中心处(r/R=0.1)，炉料不同高度下的速率分别为0.38 m·s-1(H=1 m)，0.37 m·s-1(H=2 m)，0.36 m·s-1(H=3 m)，速率均较高，且变化不大；靠近炉壁处 (r/R=0.7)，炉料不同高度下的速率分别为0.05 m·s-1(H=1 m)，0.08 m·s-1(H=2 m)，0.10 m·s-1(H=3 m)，总体靠近炉壁处速率均较小。竖炉3.8 m以下物料运动速率沿径向变化均较大。

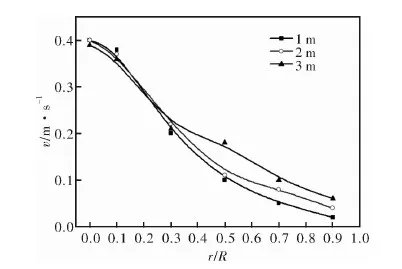
图8 竖炉纵截面物料运动速率分布(H=6 m)

3.3 影响效果分析

为了进一步量化竖炉高度对物料运动行为的影响，对不同高度下的模型分别取竖炉高度1 m、2 m、3 m处物料速率沿径向分布进行对比。

图9为高度1 m处不同模型的对比，三种模型物料运动速率沿径向显著减小，其中10m和8m高竖炉变化趋势相近，最大速率差分别为0.34 m·s-1、0.35 m·s-1，两条曲线接近重合。6 m高竖炉速率差别最大，为0.38 m·s-1。

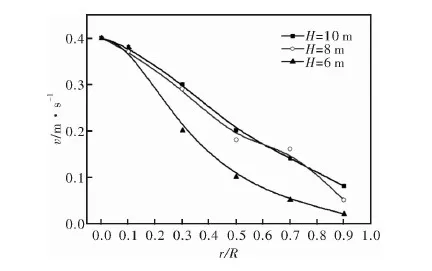
图9 不同竖炉高度纵截面物料运动速率分布(H=1 m)

图10为高度2 m处不同模型的对比，与1 m处相比，10 m和8 m高竖炉物料运动速率沿径向降低幅度显著减小，其中最大速率差分别为为0.2 m·s-1，0.22 m·s-1，分别降低了41.2%、37.1%。6 m高竖炉速率差仍然较大，为0.36 m·s-1，与1 m处相比仅降低5.3%。

图11为高度3 m处不同模型的对比，与1 m处相比，10 m和8 m高竖炉物料运动速率沿径向降低幅度进一步减小，其中最大速率差分别为为0.1 m·s-1，0.07 m·s-1，分别降低了72.2%、80%。6 m高竖炉速率差仍然较大，为0.33 m·s-1，与1 m处相比仅降低13.2%。

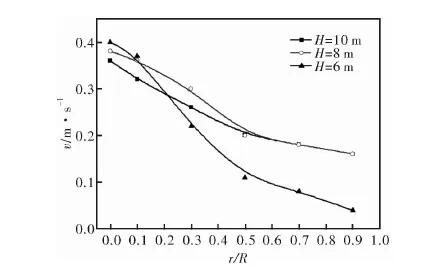
图10 不同竖炉高度纵截面物料运动分布(H=2 m)

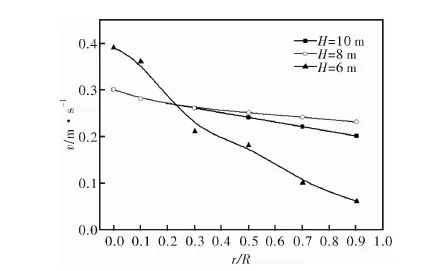
图11 不同竖炉高度条件下纵截面物料运动速率分布(H=3 m)

通过上述定性定量分析可知，竖炉高度从10 m降低到8 m时，对物料运动变化影响较小，而当进一步降低到6 m时，影响显著。竖炉高度为6 m，直径为5 m，即高径比为1.2时，物料在高度3.8 m以下运动速率沿径向分布极不均匀。为了降低这种不均匀性，获得更理想的流型分布，可通过改变螺旋输送机叶片尺寸的方法，研究其对炉料运动行为的影响。

4 结论

通过离散单元法建立了竖炉内炉料颗粒运动仿真模型，研究了不同高度及螺旋输送机参数对炉内物料运动的影响，主要结论如下：

(1)研究发现针对传统Midrex竖炉(D=5 m，H=10 m)，物料在竖炉上部运动速率沿径向分布较为均匀，在竖炉下部速率分布不均，从中心向炉壁处下降速率逐渐降低。

(2)氢气竖炉(D=5 m，H=6 m)与传统Midrex竖炉相比，下层物料运动速率分布不均匀性更显著，该层高度占据总料层高度的63.3%，会对实际生产效率和产品质量带来影响。

可在此基础上进一步研究调整螺旋输送机参数对改善炉内物料运动分布均匀性的影响。

[1] 殷瑞钰. 节能、清洁生产、绿色制造与钢铁工业的可持续发展[J]. 钢铁, 2002, 37(08): 1-8.

[2] 张春霞, 上官方钦, 胡长庆, 等. 钢铁流程结构及对CO2排放的影响[J]. 钢铁, 2010, 45(05): 1-6.

[3] Sakamoto Y, Tonooka Y, Yanagisawa Y. Estimation of CO2 Emission for Each Process in the Japanese Steel Industry: a Process Analysis[J]. Energy Conveision and Management, 1999, 40(11): 1129-1140.

[4] 方觉. 非高炉炼铁工艺与理论[M].北京：冶金工业出版社, 2002.

[5] Costa A R D, Wagner D, Patisson F. Modelling a New, Low CO2, Emissions, Hydrogen Steelmaking Process[J]. Journal of Cleaner Production, 2013(46):27-35.

[6] Warner N A. Towards Zero CO2 Continuous Steelmaking Directly from Ore [J]. Metallurgical and Materials Transactions B, 2014, 45(06): 2080-2096.

[7] 徐辉, 邹宗树, 周渝生. 竖炉生产直接还原铁过程的数值模拟[J]. 材料与冶金学报, 2009, 8(01):7-11.

[8] 董雪锋, 肖兴国, 邹宗树, 等. COREX预还原反应过程的数学物理仿真[J]. 包头钢铁学院学报, 1999, 18(02): 117-120.

[9] 白明华, 葛俊礼, 龙鹄,等. 浅议我国直接还原铁技术今后的发展[J]. 重型机械, 2013(05):1-5.

[10] Minghua Bai, Hu Long, Ren Subo. Reduction Behavior and Kinetics of Iron Ore Pellets under H2-N2 Atmosphere[J]. ISIJ International, 2018, 58(06).

[11] Parisi D R, Laborde M A. Modeling of Counter Current Moving Bed Gas-solid Reactor Used in Direct Reduction of Iron Ore[J]. Chemical Engineering Journal, 2004, 104(01):35-43.

[12] 白明华, 葛俊礼, 王健,等. 浅析还原气需求量及其与炉内流场关系[J]. 重型机械, 2014(02):31-34.

[13] Kou M Y, Wu S L, Du K P, et al. Distribution of Particle Descending Velocity in the COREX Shaft Furnace with DEM Simulation[J]. ISIJ International, 2013, 53(12):2080-2089.

[14] Hou Q F, Samman M, Li J, et al. Modeling the Gas-solid Flow in the Reduction Shaft of COREX[J]. ISIJ International, 2014, 54(08):1772-1780.

[15] Zhou H, Luo Z G, Zhang T, et al. Analyses of Solid Flow in COREX Shaft Furnace with AGD by Discrete Element Method[J]. Ironmaking and Steelmaking, 2015, 42(10): 774-784.