中值滤波结合小波变换在光谱去噪中的应用

龚梦龙

（南京邮电大学 自动化学院，江苏 南京 210000）

在光谱分析中，光谱信号中往往会混有噪声，比较常见的就是脉冲干扰和高斯白噪声，这些噪声会使光谱信号的形状、位置等一些特征发生变化，让人们在分析时得出错误的结果。为了提高分析的精确度，需要对光谱信号进行去噪处理，降低信号中的噪声，提取出有用的信息，从而得到精确而正确的结果。因此，在光谱分析中一定要对信号进行滤波处理[1]。目前，已经有很多去噪方法被用来进行光谱去噪，比较常见的有均值滤波、中值滤波和小波滤波等[2]。这些去噪方法有优点也有缺点，如果只使用其中任何一种单一的滤波方法，很难做到较好的去噪。本文提出了一种中值滤波与小波变换相结合的方法，中值滤波能有效去除脉冲噪声，小波变换去噪不仅能够有效去除白噪声，还能保留信号的细节部分，但对脉冲噪声的去除能力有些差。通过实验分析，本文提出的方法能提高光谱的信噪比，恢复真实的信号，而且比其他滤波方法有更好的去噪效果。

1 去噪方法分析

1.1 小波变换去噪

小波变换是在傅里叶分析的基础上形成的一种信号分析工具，在时间和尺度2个域中都能很好地表征信号的特征[3]。小波变换将信号分解为2部分，即低频部分和高频部分，信号的主要特征在低频部分，而信号的细节则在高频部分，然后通过阈值的方式选出有用的信息，同时，剔除噪声，最后将信号重构，得出去噪后的信号。设含噪信号为：

式（1）中：S（t）为原始信号；y（t）为有用信号；n（t）为噪声。

小波变换去噪的一般步骤为[4]：①对含噪信号进行小波变换分解，选择合适的小波基和分解层数N分解信号，得到小波分解系数；②对于分解得到的高频系数，选择合适的阈值函数进行阈值化处理；③信号重构，即将低频系数和经过处理后的高频系数通过小波重构，得到去噪后的信号。

在小波变换去噪方法中，最重要的是选择合适的小波基和阈值函数，不同的小波基和阈值函数影响着信号去噪质量。常用的阈值函数有硬阈值函数和软阈值函数2种[5]，硬阈值能很好地保护信号的局部特征，但丧失了原有信号的平滑性；软阈值处理后的数据较为平滑，但是，会模糊信号边缘[6]。2种阈值函数的表达式为[7]：

硬阈值函数为：

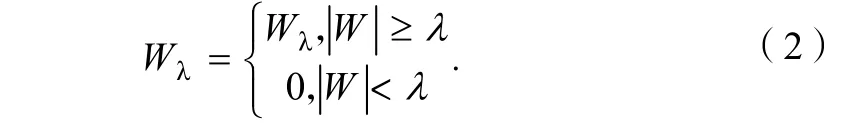
软阈值函数为：

对于阈值函数，选择合适的阈值λ非常关键，阈值太大，会除去较多的信号，造成有用信号的缺失；阈值太小，去噪后的信号里会掺杂较多的噪声，达不到去噪的效果。

1.2 中值滤波去噪

Turkey首次提出的中值滤波去噪方法是一种非线性平滑去噪技术，它能够有效抑制噪声。其基本原理是，利用窗口在数据序列上滑动，对窗口中的数值重新排序，选出中间值并与窗口中的原中间值替换[8]。因为中值滤波过程中并不添加新的数据，所以，去噪后得到的信号与原始信号贴近，保证了信号的准确性。中值滤波器输出值为：

式（4）中：yi为输出的中间值；xk和xk＋1为原始的中间值；n＝2k＋1和n＝2k为窗口大小。

由此可见，在中值滤波中，选择合适的窗口大小是关键，不同的窗口去噪效果也是不同的。

2 中值滤波与小波变换相结合去噪

中值滤波对脉冲信号有很好的抑制作用，能够很好地保护信号边缘，让它免于模糊，而且在滤波的过程中不加入额外的数据，保证了信号的准确性[9]。而小波变换去噪能够很好地去除高斯噪声，同时，又能够保留信号的细节部分[10]。因此，本文将2种滤波方法相结合，不仅能够有效去噪，还能够保留信号的细节部分。

中值滤波与小波变换相结合去噪的步骤是：①选择合适的小波基和分解层数，对信号进行小波变换，得到分解后的低频系数和高频系数；②对于高频系数部分，利用合适的阈值函数进行阈值化处理，得到处理后的高频系数；③重构低频系数和高频系数，得到初步去噪后的信号，然后使用小波变换进行一层分解；④由于信号中的噪声主要是高频信息，所以，保留低频系数，对高频系数使用中值滤波处理；⑤将低频系数和处理后的高频系数重构为最终处理后的信号。

3 仿真结果与分析

为了验证所提出方法的有效性，本文使用信噪比和均方根误差来判断去噪效果[11]。使用光谱仪测量得到如图1所示的原始信号，加噪后形成含噪信号。

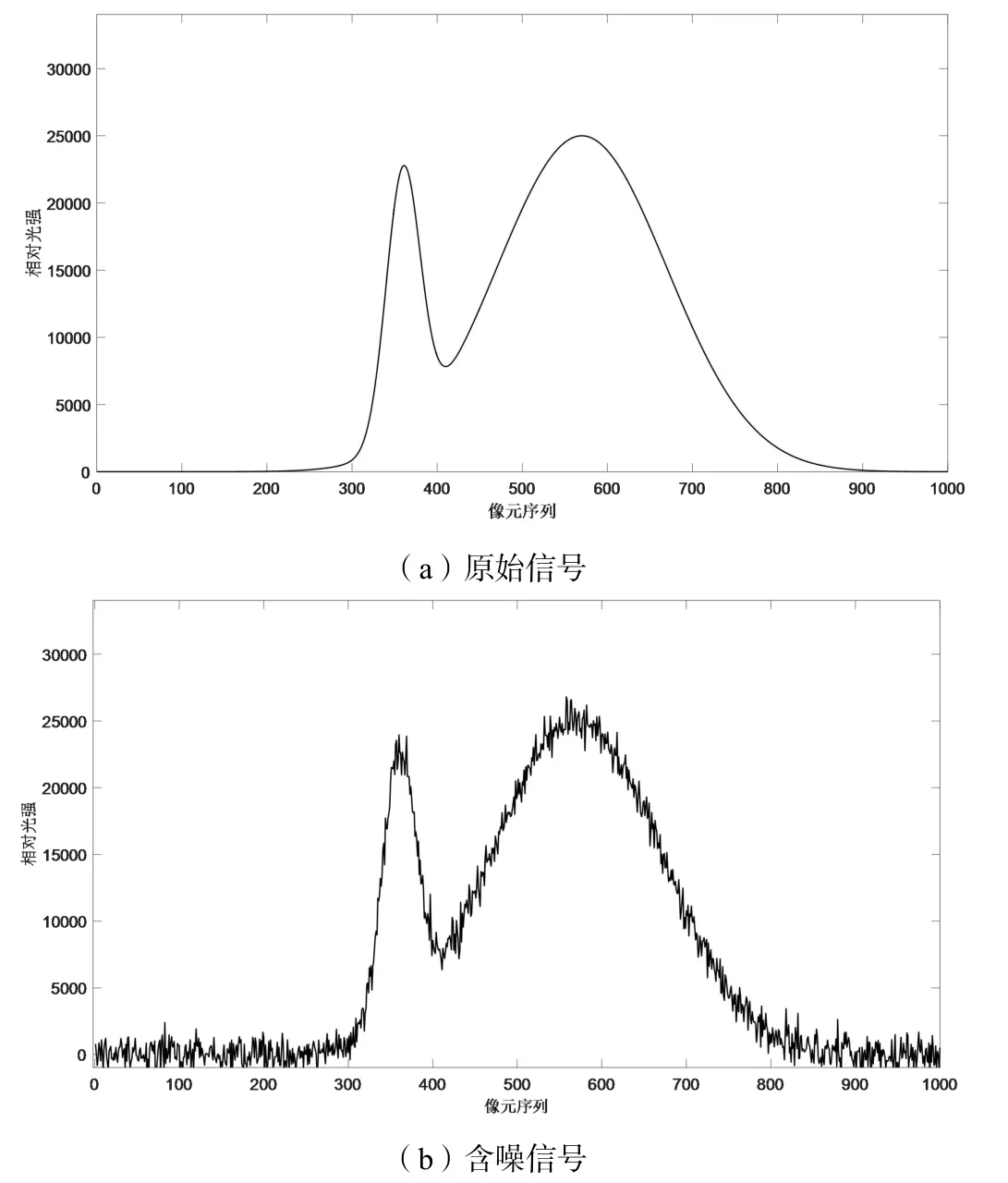
图1 光谱原始信号和含噪信号

表1 中值滤波不同窗口信噪比

使用中值滤波时，关键是要确定中值滤波器的窗口大小，窗口的大小决定了滤波的质量。为选择合适的窗口，本文选择窗口n从5开始，每次增加4个窗口，用信噪比决定中值滤波器的窗口。表1为使用各窗口滤波后得到的信噪比大小。

由表1可知，当窗口大小n＝21时，中值滤波滤波后的效果最好，信噪比最高；当n＞21时，信噪比又开始降低，所以，本文使用该窗口去噪。在使用小波变换去噪方法前，先要确定去噪相关的阈值函数和阈值、分解层数、小波基。从理论上讲，分解层数越多，去噪效果越好，但是，分解层数越多会影响运算量，本文根据实际情况选择3层小波分解。使用软阈值函数能使信号变得更为平滑，并且不会产生跳跃点。为了确定小波基和阈值，先进行模拟实验，以寻找最佳的小波基和阈值。本文选取了17种小波基，在固定阈值、启发式阈值、无偏似然估计和极大极小阈值4种阈值的情况下对加噪信号进行去噪处理[12]，根据信噪比的值进行选择。如图2所示，当阈值为固定阈值、小波基为sym8时，信噪比最大，为35.98.因此，本文使用固定阈值和sym8小波基来处理测得的光谱信号。

图2 17种小波基在不同阈值下的信噪比

图3 新方法去噪后光谱信号

确定好各种条件后，使用中值滤波与小波变换相结合去噪的方法对带噪信号进行去噪处理，得到信号如图3所示。为了评价去噪效果，本文使用信噪比和均方根误差判断去噪方法。表2为不同滤波方法滤波后的信噪比和均方根误差。

从表2中可以看出，经过新的滤波方法处理过的信号，信噪比和均方根误差都有了很大的提升，去噪效果比单一的中值滤波和小波变换滤波还要好。这说明，本文提出的去噪方法是有效果的，能更有效地对信号进行去噪。

表2 不同方法去噪后的SNR和RMSE

4 结论

针对光谱信号提出了一种新的去噪方法，该算法结合了小波变换去噪和中值滤波的优点，能有效去除光谱信号中的噪声。经过该方法去噪后的信号，信噪比有了很大的提高，同时，均方根误差也降低了很多。综上所述，本文提出的去噪方法是有效的。

［1］王瑛，莫金垣.光谱信号的小波去噪新技术［J］.光谱学与光谱分析，2005，25（1）：124-127.

［2］雷超阳，刘军华，张敏.一种基于自适应的新型中值滤波算法［J］.计算机工程与应用，2008，44（12）：60-62.

［3］闫红秀.基于4F系统的光学小波滤波器的研究［D］.重庆：重庆大学，2011.

［4］李从清，龙东，孙立新，等.一种新的基于小波变换的语音消噪方法［J］.河北工业大学学报，2008，37（3）：43-47.

［5］缑新科，郭天圣.基于一种新型小波阈值函数的信号去噪［J］.西北师范大学学报（自然科学版），2010，46（1）：51-54.

［6］Donoho D L.Denoising by soft thresholding［J］.IEEE Transactions on Information Theory，1995，41（3）：613-627.

［7］刘艳萍，高果荣.提升小波变换与中值滤波结合的红外光谱消噪［J］.光谱学与光谱分析，2012，32（8）：2085-2088.

［8］黄敏超，高美凤.基于小波阈值组合滤波器的光谱去噪方法［J］.江南大学学报（自然科学版），2015，14（2）：136-140.

［9］姜春苗.图像中高斯-脉冲复合噪声的抑制算法研究［D］.西安：西安电子科技大学，2009.

［10］吴秀君.改进提升小波阈值算法在信号去噪中的应用［J］.激光杂志，2014（8）：15-18.

［11］席旭刚，武昊，罗志增.基于EMD自相关的表面肌电信号消噪方法［J］.仪器仪表学报，2014（11）：2494-2500.

［12］于笃发，邵建华，张晶如.基于小波自适应阈值图像去噪方法的研究［J］.计算机技术与发展，2013（8）：250-253.