基于LSTM模型的短期负荷预测

张亚宁

（华北电力大学 数理学院，北京 102206）

1 引言

电力系统是由电网和用户组成，需要满足不同用户的各类负荷需求。由于电能具有不可存储性，电能的生产、输送、调度和消费实质是同时进行的闭环。为了保证电力系统运行的可靠性和经济性，需要制订合理的计划和调度方案，而准确的电力负荷预测是必要的前置条件。短期负荷预测（Short Term Load Forecasting，STLF）是其中重要的组合部分。短期负荷预测主要是指，预报未来几小时、一天至几天的电力负荷。英国的研究结果表明，短期负荷预测的误差每增加1%将导致每年运行成本增加约1 770万英镑。在挪威，每增加1%的短期负荷预测误差将增加455～910万欧元的附加运行成本[1]。

根据用户用电体量和习惯的不同，可将用户分为居民用户、商业用户和工业用户。其中，工业用户一般配有智能表计装置，其耗电量大、自动化程度高，具有开展智能用电管理的良好基础。我国国家能源局发布的2017年全国电力工业统计数据显示，我国工业用电在全社会用电中所占的比例较大，约86%[2].因此，工业用户作为智能化用电的行为主体，在智能电网的需求响应、节能减排中起着至关重要的作用[3]。

如果能提高工业用户的负荷预测精度，将对电力系统规划和优化运行有着重要的影响。然而，工业用户负荷受天气、温度、经济、政治等因素的影响很大，工业用户的短期负荷预测是一个复杂的问题，传统的预测方法难以精确预测。

2 国内外研究现状

短期负荷预测的传统模型分为两类，第一类是处理时间周期性变化的负荷数据最常用到的时间序列模型。典型的时间序列方法有Box-Jenkins模型预测[4]、ARMA模型预测法[5]等。该类方法所构建的预测模型简单，应用较为广泛，但对负荷序列的平稳性要求比较高。在大多数情况下，只利用历史负荷进行预测，在某些情况下，预测精度会受到影响。为了克服这些缺陷，随着人工智能和智能电网的迅速发展，适应大数据的第二类机器学习模型已成为研究主流。以人工神经网络（Artificial Neural Network，ANN）、支持向量机（Support Vector Machine，SVM）、随机森林（Random Forest，RF）为代表的浅层机器学习算法凭借良好的非线性函数拟合能力已成为该领域的研究热点。这些方法的改进和组合在一定程度上改善了负荷预测精度提高受限的问题。

人工神经网络具有对样本数据容错率高、非线性映射能力强、自适应和自组织等优点[6]，但BP（Back Propagation，BP）网络的缺陷在于容易陷入局部最小点。

支持向量机也是现在负荷预测的主流方法之一。支持向量机是一种监督学习模型，在解决小样本、模式识别中表现出许多优势。但是，SVM算法在大规模训练样本中难以实施。由于SVM是借助二次规划来求解支持向量的，而求解二次规划将涉及高阶矩阵的计算，所以，当样本数目很大时，该矩阵的存储和计算将耗费大量的机器内存和运算时间[7]。随机森林具有较好的泛化性能且对噪声不敏感等优点，常常用于负荷预测中。但是，随机森林在某些噪声较大的样本上会产生过拟合的问题[8]。

这些方法都是使用机器学习的方法寻找负荷影响因素与负荷之间的非线性映射关系，而忽略了连续负荷样本之间的序列数据的相关关系。实际上，作为典型的时间序列，负荷数据不但具有非线性，而且具有相关性，即对于给定的用户，其负荷数据的变化是一个连续的过程，当前时刻的负荷与上一时刻的负荷之间并不是相互独立的，两者存在着很强的相关性。所以，每一时刻的负荷变化不仅依赖于当前时刻的输入特征，而且与过去的输入特征也有关。因此，传统方法仅对单个样本的输入特征和输出功率建立非线性关系，丢失了连续序列样本间的强相关性，其预测精度有限。因此，本文提出了一种基于长短期记忆（Long Short-Term Memory，LSTM）神经网络的短期负荷预测方法。LSTM神经网络是改进循环神经网络（Recurrent Neural Networks，RNN）的计算单元，得到的一种改进的深度学习算法，对于处理时间序列相关的数据有良好的效果。该方法可充分利用负荷数据之间的时间相关性，从而提高负荷预测的精度。

3 LSTM网络的原理介绍

长短期记忆网络是一种改进的循环神经网络。由于其独特的设计结构，LSTM适用于处理与预测时间序列中间隔和延迟非常长的重要事件。

3.1 循环神经网络

RNN（Recurrent Neural Network）是一种专门处理序列性数据的神经网络，与普通的神经网络不同的是，RNN通过隐藏层节点周期性的连接来保存、学习和记录序列数据中的历史信息。如图1所示，RNN的结构包括输入层、隐藏层、输出层。层与层之间由权重相连接。

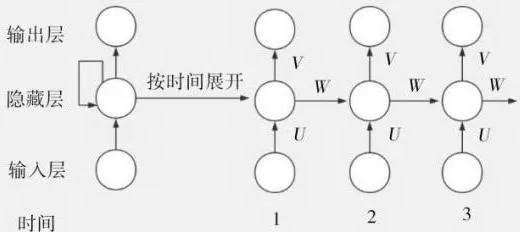
图1 循环神经网络结构

如图1所示，U，V，W分别为输入到隐藏层、隐藏层到隐藏层、隐含层到输出的权重。不同于传统的神经网络，RNN具有参数共享的思想，即层与层之间具有相同的参数U，V，W。这样大大减少了网络中需要学习的参数，缩短了模型的训练时间。但是，RNN在处理时间序列上距离较远的节点时会遇到巨大的困难，因为计算距离较远的节点之间的联系时会涉及雅可比矩阵的多次相乘，这会出现梯度消失（经常发生）或者梯度膨胀（较少发生）的问题，而长短期记忆网络可以很好地解决这个问题。

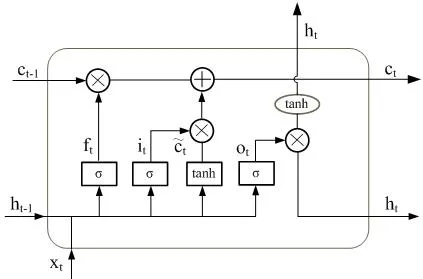
图2 LSTM结构介绍

3.2 长短期记忆网络

长短期记忆网络为了克服循环神经网络的梯度消失或爆炸的问题，在保持循环神经网络结构的基础上重新设计了记忆单元，其结构如图2所示。

每个LSTM记忆单元中含有3个控制门，分别是it、输出门ot和遗忘门ft。如图2所示，LSTM在时刻t的输入数据为xt，输出值为ht，ct为记忆状态。LSTM记忆单元更新如下。

3.2.1 遗忘门ft的计算

遗忘门主要取决于从记忆单元状态中遗忘多少信息，由t时刻输入值xt和t－1时刻隐层输出ht－1共同决定。遗忘门ft的计算公式是：

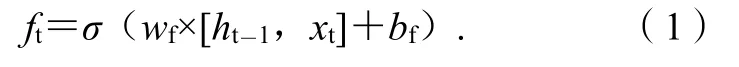
式（1）中：wf为t时刻遗忘门ft的权值矩阵；bf为偏置量；σ采用Sigmoid函数。

3.2.2 输入门it的计算

输出门主要决定当前输入数据有多少输入到记忆单元中，由t时刻输入值xt和t－1时刻隐层输出ht－1共同决定。输入门it的计算公式是：

式（2）中：wi为t时刻输入门it的权值矩阵；bi为偏置量。

3.2.3 记忆单元的候选状态的计算

由t时刻输入值xt和t－1时刻隐层输出共同决定。记忆单元的候选状态的计算公式是：

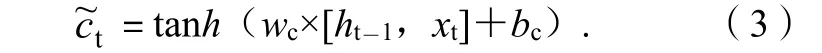
上式中：wc为t时刻候选状态的权值矩阵；bc为偏置量。

3.2.4 记忆单元状态值ct的更新计算

记忆单元通过输入门it和遗忘门ft对自身状态和当前候选记忆状态值进行调节来更新记忆单元状态。记忆单元状态值ct的更新计算公式为：

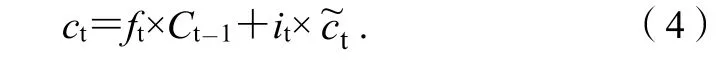
3.2.5 输出门ot的计算

输出门主要是用来控制记忆单元状态值有多少需要输出，由t时刻输入值xt和t－1时刻隐层输出ht－1共同决定。输出门ot的计算公式为：

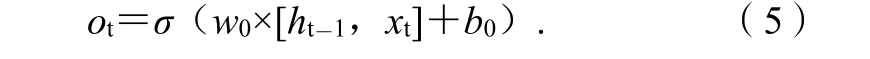
式（5）中：w0为t时刻输出门ot的权值矩阵；b0为偏置量。

3.2.6 隐藏层输出值ht计算

隐藏层输出值由t时刻输出值ot和记忆单元状态值ct共同决定。隐藏层输出值ht的计算公式是：

与传统RNN相比，LSTM增加了一个细胞状态，用来记录随着时间传递的信息。在信息传递过程中，LSTM通过当前时刻输入、上一时刻隐藏层状态、上一时刻细胞状态和门结构来增加或删除细胞状态中的信息。门结构用来控制增加或删除信息的程度，共有输入门（input gate）、遗忘门（forget gate）、输出门（output gate）3种结构门。输入门用来控制当前输入新生成的信息中有多少信息可以加入到细胞状态中，遗忘门决定上一时刻细胞状态中的多少信息可以传递到当前时刻中。LSTM基于遗忘门和输入门的输出来更新细胞状态。更新后的细胞状态由2部分构成：①来自上一时刻旧的细胞状态信息；②当前输入新生成的信息。最后，基于更新的细胞状态，输出隐藏状态。

4 基于LSTM 网络的负荷预测模型建立

4.1 数据集介绍

数据集由广州计量自动化系统采集105个工业用户近2年的电量数据得到，采样频率为15 min一个点。对于每一个工业用户，我们采取7月和8月共62 d的数据，每天有96个点。

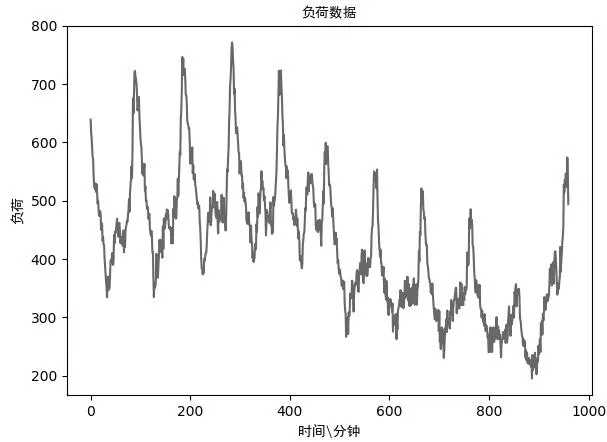
图3 负荷数据

由于每个工业用户的负荷数据特点不尽相同，所以，用单个用户的数据进行预测。在实验过程中，本文在不同种类的用户中选取最具代表性的一个用户进行实验。每个用户选取44 d的数据进行训练，18 d的数据进行测试。负荷数据具有明显的周期性和规律性，如图3所示。由于历史数据的时间相关性比较强，通过实验和统计发现，利用用电负荷序列的前10个时刻点的数据信息来预测第11个时刻点的负荷可以得到较优解，因此，LSTM的时间步长设置为10.

4.2 数据预处理

在采样过程中，存在人为操作不当、设备老化等问题，致使存在缺失值和异常数据，因此，需要进行数据预处理。负荷数据存在日周期的规律性，我们采用前一天的同一时刻的负荷数据补全。

由于LSTM及其他机器学习方法对数据尺度比较敏感，我们采用MinMax法进行归一化，归一化后的数据值域变换到[0，1]，计算公式如下：

为了提高预测精度，在负荷数据的基础上添加时刻、日期、节假日的特征。由于采样频率为15 min，1 d中共有96个点，我们采用one-hot编码的形式将时刻信息转换为96维的向量的形式，如果是某个时刻，则这个位置的值为1，否则为0.同理可得，日期信息为7维向量，节假日信息为1维向量。经过这样的处理后，每个时刻点的信息为105维的向量，对于每个用户，数据集为5 952×105的矩阵。

LSTM所使用的特征包括：过去10个时刻的负荷序列L，过去节点的时刻I，每周的周几D，是否为节假日H。LSTM的输入量X＝｛LT，ITDT，HT｝.

4.3 预测精度评价指标

预测结果误差评估标准采用平均绝对百分误差（Mean Absolute Percent Error），即：

式（8）中：为预测值；yi为真实值；n为样本容量。

4.4 LSTM结构展示

本文采用多变量单模型方法构建网络。由于LSTM网络权重共享方式与传统BP神经网络不同，LSTM网络需要学习的参数比传统BP神经网络较少，方便了模型的建立，同时对于负荷预测具有很高的精度，这也是LSTM网络在负荷预测上优于传统神经网络的地方。LSTM模型的输入节点为10个，分别为前10个数据的信息，输出节点为1个，为第11个时刻点的负荷。本文基于Keras框架下设计LSTM网络结构，LSTM的单元数为10，在LSTM结构的基础上，加入两层全连接层，激活函数分别为relu和sigmoid函数。结构如图4所示。

5 实验结果及分析

如图5所示，使用训练好的LSTM模型对测试集中的数据进行预测，并选取典型用户的某一天的数据进行展示，发现具有较高的精度。

在对比实验中，本文选取支持向量回归SVR、随机森林RF、人工神经网络ANN模型和LSTM模型作对比。在支持向量回归模型中，惩罚系数C设置为20，误差阈值设为0.1，核函数选择rbf核函数。在随机森林回归模型中，设置10个树，树的最大深度为3.在人工神经网络模型中，输入层为64个神经元，隐藏层为10个神经元，输出层为1个神经元，激活函数为sigmoid函数，迭代轮数为200轮。

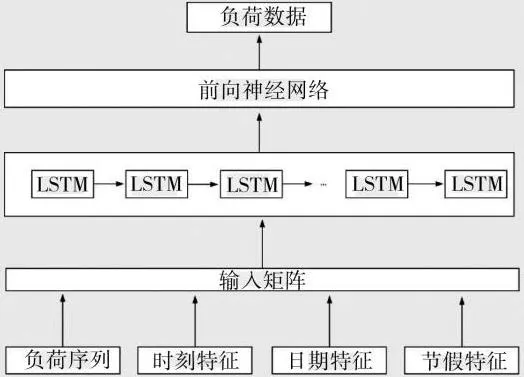
图4 LSTM模型结构

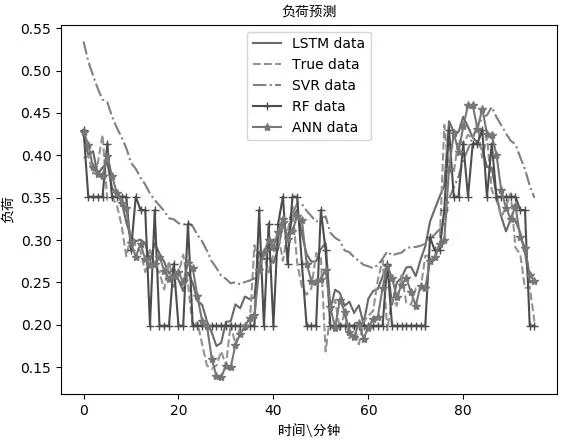
图5 预测结果与实际结果

如表1所示，选取各类工业用户中最具代表性的工业用户的预测数据进行展示。由以上结果可知，LSTM的MAPE最低可达5.82%，具有很高的准确性。同时，LSTM模型对电力负荷的预测误差显著低于别的方法，这证明了LSTM在实际中的使用效果要优于别的方法，在实际应用中有较大的价值。

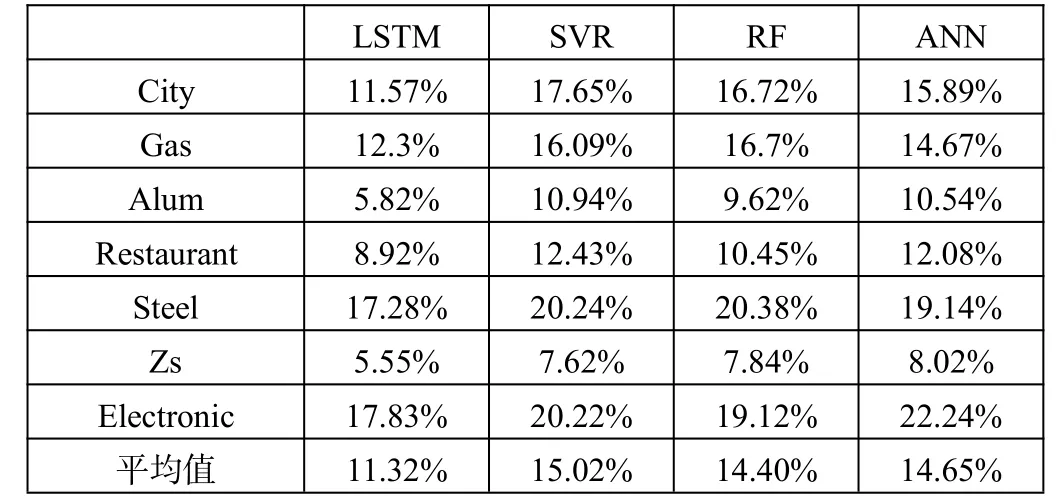
表1 各模型MAPE对比

6 结束语

本文首先分析负荷数据的特点，发现不同用户的负荷数据具有较大的差异，每个用户的负荷数据具有较强的规律性和周期性。因此，本文使用用户级数据，基于历史时刻的特征，采用LSTM网络模型。然后介绍了LSTM模型的原理和结构，解释了为什么LSTM模型适用于负荷预测。随后讨论了网络的设计，并在历史时刻的负荷数据的基础上，综合时刻、日期、节假日的信息，全方面整合历史时刻的信息，并通过one-hot编码数值化，使得输入量具有很大的信息量。最后，采用广州计量自动化系统采集的实际数据进行仿真，将数据进行预处理后输入进模型进行训练预测，结果证明基于LSTM 神经网络的负荷预测模型具有更高的精确度和更好的适用性。

［1］张宇航，邱才明，贺兴，等.一种基于LSTM神经网络的短期用电负荷预测方法［J］.电力信息与通信技术，2017（9）.

［2］中华人民共和国国家统计局.年度数据查询［EB/OL］.［2018-01-07］.http://data.stats.gov.cn/easyquery.htm?Cn=C01.

［3］王康琪.智能电网环境中基于动态价格的需求响应策略［D］.合肥：中国科学技术大学，2014.

［4］Elattar EE，Goulermas J，Wu Q H.Electric Load Forcasting Based on Locally Weighted Support Vector Regression［J］.IEEE TRansactions on systems，Man，and Cybernetics，Part C（Applicationsand Reviews），2010，40（4）：438-447.

［5］Lin W，Tu C，Yang R，et al.Particle swarm optimisation aided least-square support vector machine for load forecast with spikes［J］.IET Generation，Transmission&Distribution，2016，10（5）：1145-1153.

［6］Huaiguang Jiang，Yingchen Zhang，E Muljadi，et al.A short-term and high-resolution distribution system load forecasting approach using support vector regression with hybrid parameters optimization［J］.IEEETransactions on Smart Grid，2017，11（18）：1.

［7］Xiaoyu Wu，Jinghan He，Tony Yip，et al.A two-stage random forest method for short-term load forecasting［J］.Power and Energy Society General Meeting（PESGM），2016：1-5.

［8］Ying-Ying Cheng,Patrick P.K Chan,et al.Random forest based ensemble system for short term load forecasting［C］//Machine Learning and Cybernetics（ICMLC）.2012 International Conference，2012：52-56.