考虑发电计划的电网阻塞疏导UPFC配置研究

张大波 朱志鹏 连 帅



考虑发电计划的电网阻塞疏导UPFC配置研究

张大波1朱志鹏2连 帅1

（1. 合肥工业大学电气与自动化工程学院，合肥 230009；2. 合肥工业大学智能制造技术研究院，合肥 230009）

电网运行是一个复杂的动态过程，电力市场的激烈竞争与负荷的随机性有可能导致某些时段出现电力阻塞现象，带来安全隐患。统一潮流控制器（UPFC）可以控制线路潮流和稳定节点电压，有效缓解电力阻塞问题。为了尽量少的调整发电计划，针对现有UPFC配置方法存在未能充分考虑系统运行状态的不确定性的缺点，本文建立基于电力系统发电计划的多场景UPFC配置模型，根据季度发电计划对负荷进行场景划分，以各场景下各线路最大负载率的平均值最小为目标函数，利用遗传算法求解UPFC配置的最优方案。对IEEE-39节点系统进行算例分析，验证了该模型和算法的正确性和有效性。

电力阻塞；UPFC；配置方案；场景分析

随着电力系统规模的扩大和技术的不断发展，发电机组效率接近极限，而电力交易不断增加使得输电网络输送容量不能满足输送电能的要求，导致电力系统输电网络出现阻塞的问题[1]。电力网络阻塞会严重影响电力系统的安全性和稳定性，破坏电能正常交易，造成电力系统经济的严重损失[2]。

随着电力系统规模的不断增大以及电力市场逐渐开放，电力阻塞问题越来越严重，某些线路会出现严重过载现象，潮流值超过线路安全容量的极限。目前的研究主要从调整交易计划和优化电力系统运行参数两个方面解决电力网络阻塞问题[3-5]。文献 [6-7]从经济和管理的角度出发，以网络阻塞费用最小为目标，以输电线路有功潮流在输电线路容量的安全范围为约束，求解发电机组最优出力计划。此方案由电力市场演变而来，需要随时更新正确的电价信息。文献[8-9]利用电力系统最优潮流（OPF）算法考虑线路传输容量等约束计算发电机组最优发电计划，对发电机组进行调度，从而解决电力网络阻塞问题。但由于发电机组的出力特性具有一定的约束性，不能进行频繁、快速以及大范围的变动，并且在电力市场中，发输电的过程需要遵从发电站与各供电公司的合同条约，发电计划合约的修改不具有即时性，其效率不高。以上方法均是通过调整发电机组的发电计划来达到系统的优化运行从而消除输电线路阻塞的，但在实际应用中都有着无法避免的缺陷。

UPFC可以控制线路潮流、稳定电压、平衡负载，是一种功能强大的柔性交流输电装置[10]，在电力系统中安装UPFC能够有效消除输电线路阻塞。目前研究UPFC消除输电线路阻塞主要针对UPFC的数字仿真及控制策略[11-13]。而UPFC在电网中安装的位置和容量对于优化电力系统运行、消除线路阻塞的效果有直接影响，为了充分发挥UPFC的控制效能，研究UPFC的最优配置方案具有重要意义。

针对现有文献在疏导电力阻塞方面主要采用频繁调整发电计划以及未充分考虑系统运行的不确定性的问题，本文提出考虑发电计划的电网阻塞疏导UPFC配置模型。基于季度发电计划对系统负荷进行场景划分，以各场景下各线路最大负载率的平均值最小为目标求解UPFC最优化配置方案。

1 UPFC最优配置模型

1.1 UPFC结构原理

UPFC的基本结构如图1所示。UPFC装置由两个结构相同的电压源型变流器（VSC1、VSC2）组成，两个变流器通过一个并联的直流电容构成有功功率的变换系统。变流器VSC1通过并联变压器T1与电网耦合，向系统提供并联的无功补偿，控制节点的节点电压；变流器VSC2通过串联变压器T2与电网耦合，改变输电线路中等效的电压源幅值和相位参数，从而实现电力线路潮流调节的功能。

图1 UPFC安装位置

1.2 UPFC的稳态计算模型

考虑到UPFC在稳态运行时的主要作用是稳定节点电压和调节线路潮流，本文采用了节点分裂的方法建立UPFC稳态等效模型[14]。

图2 UPFC潮流计算模型

1.3 目标函数

本文考虑现有UPFC配置方法未能充分考虑系统运行状态的不确定性的缺点，以各场景下各线路最大负载率的平均值最小为目标函数，建立基于电力系统运行的多场景划分的UPFC配置模型，即

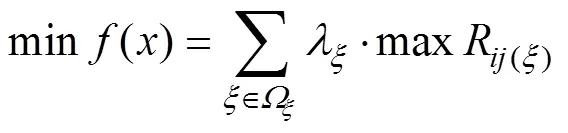
式中，()为各场景下线路最大负载率的平均值；W为场景集合，l为场景的概率()为场景中电力系统中输电线路的负载率为

其中

式中，()为场景中线路的有功功率，(max)为线路的有功限额；节点为与节点通过线路相连的节点；()为场景中节点的电压，、分别为节点导纳矩阵第行、第列元素的实部与虚部，()为场景中节点和节点的电压相角差；若UPFC的安装容量按照每10MVA一个量级配置，则模型优化变量可表示为

式中，为UPFC安装位置的线路编号，为安装位置的节点标识，当=0时，表示UPFC安装在靠近节点的位置，控制节点电压；当=1时，表示UPFC安装在靠近节点的位置，控制节点电压。为UPFC的安装容量（MVA）。

1.4 约束条件

1）等式约束

系统装上UPFC后，含有UPFC线路的潮流发生了变化，需要在普通潮流方程中增加UPFC的附加潮流，表示为

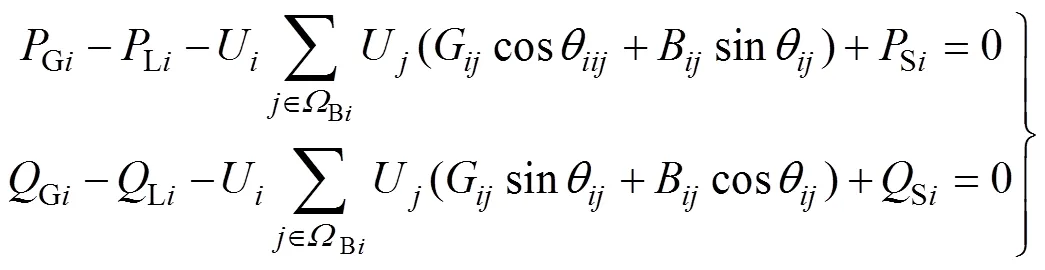
式中，G、G分别为发电机的有功无功出力；L、L分别为节点的有功负荷和无功负荷；S、S分别为UPFC对节点附加注入的有功功率和无功功率；Bi为与节点相连的节点的集合。

2）不等式约束

系统不等式约束条件

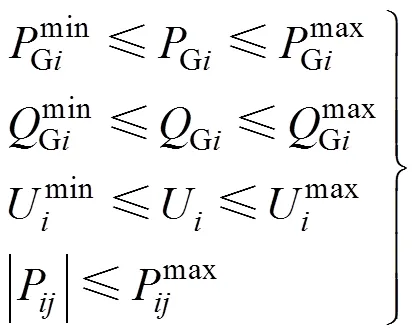
UPFC进行潮流优化计算时，需对其控制变量进行约束，约束条件如下：

式中，S、S分别为UPFC控制线路的有功功率和无功功率；s为UPFC控制线路节点电压。

对UPFC安装配置的时候需要考虑UPFC成本上限，其成本约束条件如下

UPFC的安装成本计算公式如下

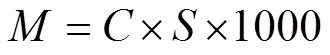
式中，为UPFC最优安装容量（MVA）；为单位容量UPFC的投资成本(＄/KVA)。max为UPFC安装成本的最大预算值；由于UPFC在工程安装中需要有一定裕度，所以取10MVA作为一个量级安装UPFC。

1.5 基于季度发电计划的系统负荷序列场景划分

目前我国的电力系统发电计划主要按年度发电量签订合约。为了能够保障落实年度合约电量，年发电量需进行阶段性分解。由于我国电力系统主要使用燃煤机组，其出力特性具有一定的约束性，不能出现频繁、快速以及大范围的变动，因此在完成年合约电量的同时，应尽量使得发电计划调整最小。随着电力系统规模不断增大，系统运行的不确定性也越来越多，有可能导致某些时段在电网的局部区域出现电力阻塞。本文通过研究UPFC的最优配置方案，修正调控电网运行的不确定性因素，使得在发电计划调整较小的前提下实现电网阻塞疏导。

场景是一种描述随机过程的方法。对负荷序列进行场景划分，每个场景都代表一种电力系统的运行状态。考虑实际的发电计划以及一年12个月用户负荷的共同性和差异性，将发电计划分为春夏秋冬4个阶段，收集整理负荷每季度2168h的序列数据，根据大量负荷的历史数据，对每个季度的负荷序列数据采用-means聚类方法得到多种场景。综合发电计划以及负荷序列数据将不确定性的电网运行状态转换为确定性的多个场景，可以最大限度地拟合电网运行状态，以此来评估UPFC对系统运行的控制作用，更有利于指导UPFC的优化配置。

某一阶段发电计划中的负荷序列的场景计算步骤如下：

1）给定聚类数，以负荷的一个季度2168h的序列数据作为样本随机选取个初始聚类中心。

2）计算每一个样本点到个初始聚类中心的欧氏距离，比较每个样本点与初始聚类中心的距离，将距离聚类中心最近的点与其初始聚类中心作为同一簇：

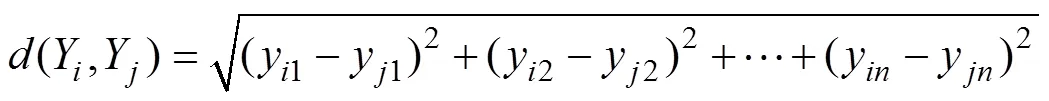
3）将点集分好簇以后，使用每个簇的样本均值作为新的聚类中心：

式中，为该簇包含的维数据样本数量。

4）重复步骤2）和步骤3），直至聚类中心不再变化为止。

5）计算场景概率。分配完所有序列数据之后，确定每一个簇中包含的序列数据的数量，则场景的概率l计算式为

2 基于改进遗传算法的UPFC优化配置模型求解

遗传算法是一类由生物界优胜劣汰、适者生存的遗传机制演化而来的随机迭代搜索算法，根据生物可进化理论，遗传算法的目标是在当前群体产生优于现有个体的个体。

其可以直接对变量的编码而非变量本身进行操作，没有函数连续性的限制；通过选择、交叉和变异3种形式，具有了强大的全局寻优能力，并且可以自适应调整搜索方向，极大提高了收敛速度[15]。

本文使用遗传算法对UPFC最优化问题求解步骤如下：

1）搜集整理一年8670h负荷大小序列的数据，并将发电计划按季度分成4类。

2）基于K-means聚类方法对各发电计划内的负荷序列进行场景划分。

3）建立考虑发电计划的基于多场景分析的电网阻塞疏导UPFC最优配置模型。

4）确定目标函数优化变量。

5）编码。对待优化变量进行编码。

6）初始种群的产生：

7）计算每个个体的适应值。对系统进行潮流计算，求出每个个体的个体适应值。

8）判断个体解的可行性。由于在进行迭代计算的过程中会出现潮流不收敛或不合理的解，对最优化结果产生干扰，对每一个个体进行可行性的判断，个体的可行解标识为“1”，个体的不可行解标识为“0”。

9）应用复制、杂交和变异算子产生下一代群体。

10）把最好的个体串指定为遗传算法的执行结果，终止判定。将算法进行终止条件判断，如果满足条件，或己经进化到规定的代数，则结束算法，输出最优解；否则代数加1，返回步骤3）。

经过以上步骤，最终得出满足约束条件的UPFC最优配置方案。

本文利用遗传算法对UPFC最优配置方案求解的流程图如图3所示。

图3 UPFC优化配置流程

3 算例分析

为了验证本文所提算法和模型的有效性和合理性，本文使用在IEEE-39节点系统的节点对UPFC优化配置模型进行计算，并对优化结果进行分析和对比。

3.1 场景划分结果

对一年发电计划与负荷数据进行场景划分，由于场景数过多会造成计算量较大，较为繁琐，场景数过少会使结果不够精确，因此，本文通过使用聚类的有效性指标，选择适用于K-means聚类的CH(+)指标[16]（Calinski Haraba-sz Index, CH(+)）将每一个发电计划中的负荷序列的最佳聚类数确定为5，即为5个场景，四类发电计划共20个场景。表1给出各场景的概率。

IEEE-39节点系统中节点编号为31—39的发电机组在四类发电计划中的出力情况见表2，其中节点30上的机组为平衡节点。

图4 IEEE 39节点系统图

表1 场景概率

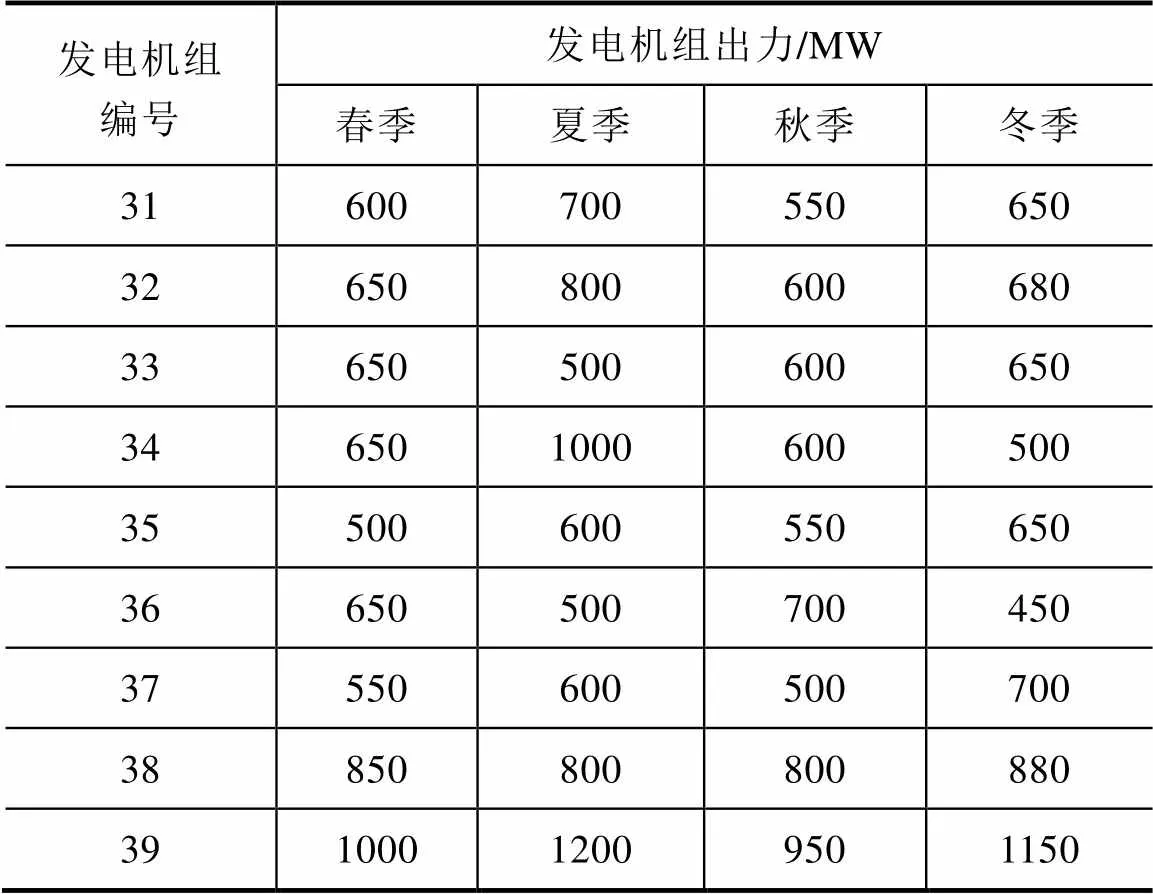
表2 四类发电计划中机组出力大小

在春季阶段的发电计划中5种场景下负荷的大小序列如图5所示。

图5 春季发电计划中负荷的5个场景下的大小序列

3.2 计算得到最优解

对目标函数进行遗传算法最优计算得到方案如下，并与未优化情况以及未考虑发电计划更改和运行场景变化时的配置方案对比，见表3。

表3 优化结果对比

最优方案中UPFC安装在17—18支路上靠近节点17的位置，控制节点17电压，安装容量为120MVA；最优方案中线路的最大负载率相对于未优化情况减小34.34%。而作为对比的只考虑单一场景的配置方案相对于未优化情况减小了28.04%，可以看出UPFC对于电力系统系统的输电网络阻塞问题有很大的改善作用，且基于多场景划分的最优方案明显要优于只考虑单一场景的优化配置方案。图6给出4类发电计划20个场景下IEEE 39节点系统的线路最大负载率优化前后的对比。

图6 线路最大负载率对比

图6给出了多场景下UPFC最优配置方案与只考虑单一场景的UPFC最优配置方案对系统线路堵塞问题的优化效果对比，当未安装UPFC时其中几个场景中线路的最大负载率已经超过1，已经威胁到电力系统运行的安全性了，安装UPFC进行优化之后，最优化方案中线路最大负载率均未越限，使得电力系统在安全范围内运行，各线路负载更加均衡，有效地解决了电力线路的堵塞问题，而只考虑系统单一运行场景的配置方案使得系统运行的大部分场景中越限情况也得到一定的改善，但在场景10和场景18下线路的最大负载率仍处于越限状态，此时易发生安全问题，说明该方案并不完美，因此，通过多场景划分确定UPFC的最优配置方案，可以使电力系统在发电计划调整较小的情况下解决网络拥堵问题，而不考虑多场景划分对UPFC进行优化配置效果并不能使系统运行状态发生变化时得到足够的安全保障，其得到的最优配置方案并不实用。由此验证了本文所提出的优化模型及算法的有效性和正确性。

4 结论

在考虑发电计划的情况下，针对电力系统运行状态发生变化时某些时段可能出现输电线路阻塞的问题，通过安装UPFC疏导线路阻塞。为了充分发挥UPFC的控制效果，本文构建了以各场景下各线路最大负载率的平均值最小为目标函数的UPFC最优化配置模型，通过K-means聚类对不同发电计划下的负荷序列进行场景划分，采用分裂节点的方法对加入UPFC的电力系统进行潮流计算，得到UPFC的最优配置方案。通过仿真计算并对比多场景与单一场景下对解决系统线路阻塞问题的作用与差异，验证了考虑多场景划分的UPFC最优配置方案的优势以及改善网络阻塞的作用，表明了本文所提模型和算法的正确性和有效性。

[1] 高赐威, 程浩忠. 电力市场环境下电网规划的若干问题研究[J]. 华东电力, 2005, 33(3): 5-10.

[2] Wang R, Lasseter R H. Re-dispatching ration to increase power security margin and support low voltage bus[J]. IEEE Transactions on system Power, 2000, 15(4): 496-501.

[3] 姚建刚. 区域电力市场竞价交易结构与模式的探讨[J]. 电力系统自动化, 2003, 27(22): 23-25, 55.

[4] 肖宏飞, 李卫东, 魏立明. 基于阻塞支路潮流变化量的阻塞成本分摊[J]. 中国电机工程学报, 2004, 24(2): 83-87.

[5] 王秀丽, 甘志, 雷兵, 等. 输电阻塞管理的灵敏度分析模型及算法[J]. 电力系统自动化, 2002, 26(4): 10-13, 22.

[6] 何大阔, 王福利, 毛志忠. 基于改进遗传算法的电力系统经济负荷分配[J]. 控制与决策, 2007, 22(2): 230-232, 237.

[7] Fang R S, David A K. Optimal dispatch under transmission contracts[J]. IEEE Transactions on Power Systems, 1999, 14(2): 732-737.

[8] 孙元章, 焦晓红, 申铁龙. 电力系统非线性鲁棒控制[M]. 北京: 清华大学出版社, 2007.

[9] 卢强, 王仲鸿, 韩英铎. 输电系统最优控制[M]. 北京: 科学出版社, 1982.

[10] Gyugyi L A. Unified power flow control concept for flexible AC transmission systems[J]. IEEE Proceedings, 1992, 139(4): 323-331.

[11] Ba A, Tao P, Lefebvre S. Rotary power-flow controller for dynamic performance evaluation-part I: RPFC modeling[Z]. 2009.

[12] Yuan Z C, Song Q, Liu W H, et al. Nonlinear controller for unified power flow controller[J]. Automation of Electric Power Systems, 2005, 29(19): 36-39.

[13] 刘黎明, 康勇, 陈坚, 等. UPFC的交叉耦合控制及潮流调节能力分析[J]. 中国电机工程学报, 2007, 27(10): 42-48.

[14] 庄海军. UPFC的选址及网损优化计算[J]. 黑龙江电力, 2014, 36(6): 491-495, 501.

[15] 葛洪伟, 王银年. 遗传算法的研究与应用[D]. 无锡:江南大学, 2009.

[16] 周开乐, 杨善林, 丁帅, 等. 聚类有效性研究综述[J]. 系统工程理论与实践, 2014, 34(9): 2417-2431.

Allocation schemes research of UPFC based on relieving power blockage considering the power generation schedule

Zhang Dabo1Zhu Zhipeng2Lian Shuai1

(1. School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009; 2. Intelligent Manufacturing Institute, Hefei University of Technology, Hefei 230009)

Power grid operation is a complex dynamic process, the intense competition of electricity market and the randomness of load may lead to the phenomenon of power blockage in some period, and cause security hidden troubles. The Unified Power Flow controller (UPFC) can control the line powers flow and stabilize the node voltage, and effectively alleviate the problem of electrical congestion. In order to adjust the power generation schedule as little as possible, in view of the shortcoming of the existing UPFC configuration method has not fully considered the uncertainty of system operating state, this article establishes a various screens UPFC configuration model based on power system generation schedule, and divides the load according to the quarterly power generation plan, takes the minimum average value of maximum load rate of each line in each scene as the objective function, and uses the genetic algorithm to solve the optimal scheme of UPFC configuration. An analysis of IEEE-39 node system is presented to verify the correctness and effectiveness of the model and algorithm.

power blockage; unified power flow controller; allocation schemes; scenario analysis

2017-12-19

张大波（1979-），男，合肥工业大学讲师，博士，研究方向为电力系统可靠性评估、电网规划运行、电力设备维修优化。

国家自然科学青年基金资助项目（51407056）

中国博士后科学基金面上资助（2014M561819）