基于综合干旱指数的淮河流域土壤含水量反演
张 文, 任 燕, 马晓琳, 胡艺杰
(1.武汉大学遥感信息工程学院,武汉 430079; 2.国家知识产权局专利局专利审查协作河南中心,郑州450046; 3.河南省白沙水库管理局,禹州 461670; 4.华北水利水电大学资源与环境学院,郑州 450045)
0 引言
陆表土壤水不仅是旱情监测的重要指标,还是气候、水文、生态、农业等领域的重要参数,也是全球气候变化的重要组成部分[1]。传统测量方法只能采集到点和小范围的墒情信息[2],而遥感技术的发展为获取大范围地表土壤水分提供了有效手段。遥感的主要特点是探测范围广、速度快、周期短、受地面条件限制少,能够频繁持久地提供地表的信息[3]。因此,利用遥感技术来进行大区域的土壤水分信息提取具有极其广阔的应用前景。
从20世纪60年代开始,遥感技术已经开始应用到土壤水分监测中,历年来,国内外科研工作者提出过许多模型和方法。1969年,Jordan[4]提出了最早的一种植被指数,比值植被指数(ratio vegetation index,RVI); 1977年,Kahle[5]得到第一个遥感热惯量影像; Price给出了用遥感数据计算热惯量的一般方法[6],并于1985年提出了表观热惯量(apparent thermal inertia,ATI)模型[7]; Jackson等[8]综合分析研究土壤水分、叶片温度和植被指数相互之间关系,于1981年提出了作物缺水指数法(crop water stress index,CWSI); Carlson等[9]于1994年提出了综合考虑植被指数和植被冠层温度的植被供水指数(vegetation supply water index,VSWI); 2002年,Sandholt等[10]运用陆地表面温度(land surface temperature,LST)与归一化植被指数(normalized differential vegetation index,NDVI),建立了NDVI-Ts特征空间,并提出了温度植被干旱指数(temperature vegetation dryness index,TVDI)。各种干旱指数都有其优缺点与不同的适用范围,综合多种干旱指数对土壤水分进行反演会得到更可靠的效果。因ATI模型与VSWI模型计算简便,效果良好,本文选取这2种模型进行实验。已有研究表明ATI模型只适用于低植被覆盖区域[11],而VSWI模型在作物覆盖度较高时比较有效[9],本文通过NDVI来区分地表植被覆盖度,结合ATI与VSWI模型,建立综合干旱指数(comprehensive drought index,CDI)模型,进行土壤水分的初步反演。
但是仅利用遥感数据来监测土壤水分也有不足,因为利用上述模型基于遥感影像提取到的土壤水分信息都只能反映土壤的相对干湿情况,并不是真实的土壤含水量值,对土壤含水量的定量分析和使用有较大的限制。因此,本研究引入实测的土壤含水量数据,探究CDI结果与实测土壤含水量之间的相关关系,选出一种最佳的相关模型,则可利用该模型把CDI结果转化为真实的土壤含水量数据,以期提高大区域的陆表土壤含水量监测效率,便于土壤水分产品的业务化生产。
1 研究区概况及数据源
1.1 研究区概况
淮河流域地处我国东部,介于长江和黄河2流域之间,位于E111°55′~121°25′,N30°55′~36°36′,面积约27万km2(图1)。淮河流域西部、西南部及东北部为山区、丘陵区,其余为广阔的平原[12]。平原面积约占总面积的2/3,在我国农业生产中占有重要地位。

图1 研究区及实测站点示意图
淮河流域地处我国南北气候过渡带,冬春干旱少雨,夏秋闷热多雨,冷暖和旱涝转变急剧,多年平均降水量约为920 mm,由南向北递减,山区多于平原,沿海大于内陆,旱涝时有发生。因此,对淮河流域进行业务化的土壤含水量监测具有极大的价值。因其流域面积大,地貌特征复杂,利用MODIS影像选取ATI和VSWI模型进行综合研究,是一种有效可行的方法。
1.2 数据源
1.2.1 MODIS数据
MODIS数据是美国国家航空航天局(National Aeronautics and Space Administration,NASA)对地观测系统系列遥感卫星平台上的主要传感器,它具有36个光谱通道,每1~2 d可以获取一次全球地表数据[13]。因其波段范围广,数据更新频率快,在全球范围免费接收等优点,本实验选用MODIS数据为主要数据源[14]。
选取空间分辨率为1 000 m的MODIS 1B产品数据,即MOD021KM, 以及其对应的地理定位文件,即MOD03。使用ENVI+IDL进行编程,完成数据预处理和相关指数的计算。
1.2.2 实测数据
地面实测土壤含水量数据来自中国水利部数据中心,其墒情数据主要由水利部门的土壤墒情监测站提供。墒情监测站点以县为单元,根据气候类型、地形地貌、作物布局、灌排条件和土壤类型等因素,设置在区域范围内代表性较强的地块。墒情采集方法主要为固定监测法,即埋设固定式自动监测设备,传感器分别埋入土层深度10 cm,20 cm和40 cm处,按0~10 cm,10~20 cm和20~40 cm共3个层次监测土壤含水量,并于每月的1日、11日和21日各观测一次。
淮河流域耕地面积为1 333 hm2,农作物以冬小麦、水稻、棉花和油菜等为主。每年的5月上中旬是冬小麦的抽穗扬花期,5月中下旬为灌浆乳熟期,5月底到6月上旬为收割期,因此5月份是冬小麦生长需水的最关键时期,一旦出现旱情,则会抑制子粒灌浆及干物质向子粒的运输与积累,从而直接影响到小麦单产水平。故本文选取了2014年5月1日、11日、21日和6月1日4天作为实验日。其中5月1日、11日属于小麦生长的中后期,叶面基本覆盖农田; 5月21日和6月1日属于小麦成熟期,部分地区小麦开始收割,地表覆盖情况不一。
2 研究方法
2.1 干旱指数模型选择
目前利用卫星影像反演土壤水分的方法己经有很多,例如ATI、距平植被指数、CWSI、条件温度植被指数(vegetation-temperature condition index,VTCI)、VSWI等。现将使用比较广泛的几种方法进行介绍与分析。
2.1.1 ATI模型
土壤热惯量随土壤含水量的变化而变化,因此可建立土壤热惯量模型来监测土壤含水量。Price[7]提出的ATI是在热惯量定义的基础上,不考虑太阳高度角和纬度等因素,其形式为
ATI=(1-A)/(Tmax-Tmin),
(1)
式中:ATI为表观热惯量;A为全波段反照率,可由 MODIS数据 1和2 通道的反射率得到;Tmax和Tmin分别为一天中最高和最低温度,可分别由MODIS数据 31 通道的地表温度得到。ATI值越高,表示土壤含水量越大,反之亦然。ATI模型参数都可从遥感影像中获取,且计算简便,但仅适用于低植被覆盖区域[10]。
2.1.2 CWSI模型
CWSI以能量平衡为基础,是最常用的植被蒸散法之一,定义为[15]
CWSI=1-ET/ETp,
(2)
式中:CWSI为作物缺水指数;ET为水分的日蒸散量;ETp为在水分供应充分条件下的日潜在蒸散量。ET值越小,CWSI值越大,土壤的含水量也越少,反之亦然。但是ET与ETp值不能够从遥感影像上直接获取,需要大量的地面实测资料,应用起来也比较困难。
2.1.3 VTCI模型
在NDVI-Ts构成三角形空间的基础上,王鹏新等[16]提出了VTCI模型 ,其计算公式为
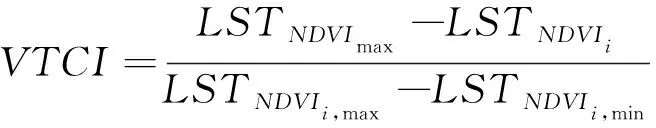
(3)
式中:VTCI为条件植被温度指数;LSTNDVIi,max和LSTNDVIi,min分别为研究区域内具有相同NDVI值的像元的最高温度和最低温度;LSTNDVImax为NDVI最大值相应像元的温度;LSTNDVIi为NDVI值为NDVIi的相应像元的温度。VTCI的值越小代表土壤含水量越低,反之亦然。该模型对大区域的旱情监测效果较好,但计算比较复杂。
2.1.4 VSWI模型
VSWI是通过计算NDVI和植物冠层温度的比值得到的,其公式为[17]
VSWI=NDVI/T,
(4)
式中:VSWI为植被供水指数;T为植被的冠层温度。VSWI值越大,表明土壤含水量越大; VSWI值越小则代表土壤含水量越小。但VSWI值是根据植被覆盖状况的变化来进行反演的,所以不适用于低植被覆盖地区[18]。
2.2 建立综合干旱指数模型
淮河流域面积大,地貌特征复杂,仅用一种干旱指数无法满足监测复杂地表土壤含水量的需求。通过2.1节对各干旱指数模型的优缺点与适用性特征的分析,可知ATI与VSWI模型效果良好且计算简便,但ATI模型比较适用于低植被覆盖地区和裸土区域,而VSWI模型适用于植被覆盖度较高的地区,所以本文结合这2种模型来建立一种新的干旱指数模型——CDI模型。
建立CDI模型需要对植被覆盖情况进行分类,而NDVI反映了植被覆盖情况,故本文利用NDVI设置阈值来区分植被覆盖类型,以便合理使用适合不同覆盖类型的指数来反演土壤水分,以提高整个区域土壤水分反演精度。已有实验证明,在NDVI>0.3的情况下VSWI非常有效[19],而在NDVI<0.35的情况下ATI非常有效[20],因此本研究阈值选为0.33。
由于ATI和VSWI的取值范围不在同一个尺度上,因此在综合使用这2种模型之前,需要把它们归一化到同一个区间范围内,以便最终建立CDI,其公式为
(5)
式中:CDIi为在任意像元点i的综合干旱指数;ATIi为任意像元点i的表观热惯量;VSWIi为任意像元点i的植被供水指数;ATImax和ATImin分别为表观热惯量的最大值和最小值;VSWImax和VSWImin分别为植被供水指数的最大值和最小值。
2.3 基于实测数据建立相关模型
根据2.2节所述的原理与公式,利用ENVI+IDL编程可以得到每个实验日的CDI结果。但CDI的结果是个无量纲常数,只能反映土壤相对的干湿情况,并不能代表土壤含水量的定量结果。为了得到CDI与实际土壤含水量之间的关系,需要在这2种数据上分别取样点进行分析,建立两者之间的函数关系,分别用经典的线性、指数和对数函数进行拟合,根据精度选择一个最佳的函数对应关系。
实测站点分布如图1所示,选择2014年5月1日的数据进行建模。因为CDI值是遥感影像反演得到的,而理论上遥感只能穿透土壤表层,所以选用0~10 cm深度的实测数据来与CDI值进行建模。根据2.2节所述,首先用ENVI编程计算得到5月1日的CDI结果; 然后用ArcGIS把实测点对应的CDI值提取出来,去掉其中CDI值为空的数据,再去掉实测点为0或极端大的异常数据; 最后留下了81组样点。这些样点均匀分布在研究区域内,基本上能代表整个研究区域的情况。
常见的用于统计建模的数学模型有3种: 线性模型、对数模型和指数模型。为了建立选择的81组数据之间的函数关系,分别用这3种模型进行拟合,然后通过比较其精度来选择最优模型。相同的置信度下,用于判定拟合优度的指标相关系数R2越大越好。通过实验,3种模型结果如图2所示。由图可知选取线性模型函数进行拟合时,R2值最高。于是拟建立线性回归关系,进一步做置信度分析,结果如表1所示。
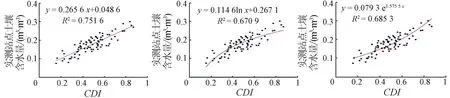
(a) 线性关系 (b) 对数关系 (c) 指数关系

图2 拟合关系对比Fig.2 Comparison of fitting relationships表1 淮河流域土壤含水量与CDI值之间的线性统计关系Tab.1 Linear statistical relationship between measured soilmoisture and CDI value in Huaihe River Basin
综上,得到了把CDI转换为真实土壤含水量值的模型,即
SM=0.265 6CDI+0.048 6,
(6)
式中SM为土壤含水量。
对该模型的可靠性进行检验,显著水平取α=0.01,R=0.87>0.283=Rn-2,α,检验通过。F=434.67>7.08=F1-α(1,n-2),检验通过。SignificanceF是在显著性水平下的Fα临界值,等于P值,故本例中,P=7.43e-34<0.001,故置信度达到99.9%以上。因此可以使用该线性模型把淮河流域的CDI结果转化为实际土壤含水量。
3 结果与分析
3.1 土壤含水量反演结果
如上述方法,利用MODIS影像计算出CDI指数后,根据线性模型式(6),反演出2014年5月11日、21日和6月1日3 d的淮河流域土壤含水量结果,如图3所示。

(a) 5月11日 (b) 5月21日 (c)6月1日

图3淮河流域土壤含水量分布
Fig.3DistributionofsoilmoistureinHuaiheRiverBasin
由图3可见,土壤含水量分布大致趋势为南部地区略大于北部地区,东部地区略大于西部地区。江苏省土壤含水量普遍较其他区域略高,可能与靠近海洋空气湿润有关。而河南和安徽等地区土壤含水量则相对略低,这主要是因为华北地区蒸发较强,夏季风弱,地下水位低。初步判断土壤含水量反演结果比较合理。整体看淮河流域土壤含水量大多在0.1~0.3 m3/m3之间,5月11日整体相对较高,5月21日整体相对较低。且5月11日土壤含水量分布不均匀,浮动较大,土壤含水量高与低的区域过度较不平缓。
3.2 精度验证及分析
为了验证本文提出的反演模型的可靠性,结合地面实测土壤含水量数据,对反演得到的土壤含水量结果进行精度验证。实测数据点去除数据为 0 和异常大值的记录,最终每个实验日选择了90个左右质量比较好的数据点。
图4为实测0~10 cm、10~20 cm深度土壤含水量与反演土壤含水量的对比。可看出反演的土壤含水量与实测土壤含水量无论是从绝对值还是变化趋势上都大体一致,特别是0~10 cm深度土壤含水量与反演结果相似度很高,只是反演值比实测值略偏低。0~20 cm深度的土壤含水量也与反演结果比较相关,但是相较而言相关性不如0~10 cm深度数据。这主要是由于遥感监测穿透土壤深度有限,所以反演结果与浅层土壤含水量的相关性更好。可以看出3个实验日中2014年5月21日土壤含水量较低,大致在0.1~0.2 m3/m3之间,在图3(b)上也有表现,其他实验日土壤含水量均在0.2 m3/m3左右浮动。

(a) 5月11日 (b) 5月21日 (c) 6月1日
图4淮河流域实测土壤含水量与反演土壤含水量对比
Fig.4ComparisonofmeasuredsoilmoistureandestimatedsoilmoistureinHuaiheRiverBasin
具体精度需要进行误差统计分析,定义地面观测土壤含水量为X,反演的土壤含水量为X0,N为参与比较的总样本数。通过对比分析,统计出最大误差(MaxE)、绝对误差(ABVR)和均方根误差(RMSE)。
3个实验日的实测0~10 cm、10~20 cm土壤含水量数据与反演得到的土壤含水量数据的误差分析如表2所示。
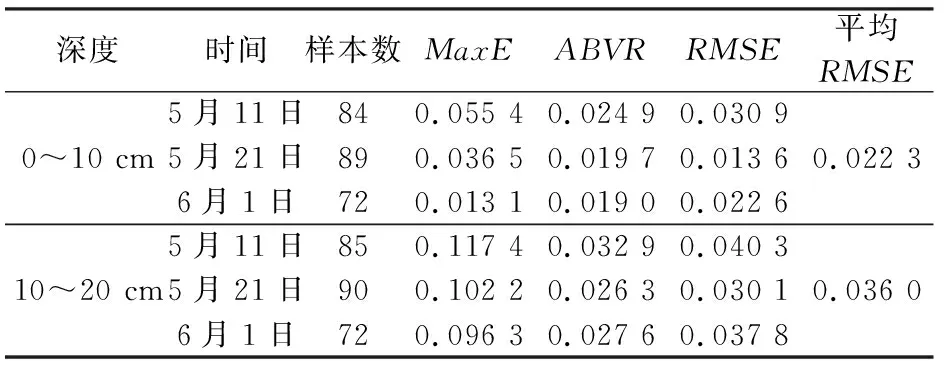
表2 实测土壤含水量与反演土壤含水量误差分析Tab.2 Error analysis of measured soil moisturewith estimated soil moisture
根据表2中的数据可知,反演精度比较理想,特别是与0~10 cm深度土壤含水量相关性较好,平均RMSE为0.022 3。而反演结果与10~20 cm深度土壤含水量的相关性略差,因为遥感只能穿透表层土壤,随着土壤深度增加,遥感反演的精度会降低。反演结果与0~10 cm和10~20 cm深度的RMSE最小值都出现在5月21日,从图3(b)和图4(b)中可以看出,当日土壤含水量在0.1~0.2m3/m3左右,相对较低。所以推断在土壤水分较低的区域,该反演模型的结果相对更加精确。而5月11日RMSE较大,从图3(a)和图4(a)中可以看出该日土壤含水量相对较高且浮动范围比较大,特别是从图3(a)可以看出土壤含水量高与低的区域过度不太平滑,可能是由于局部灌溉造成,在此种状况下模型反演精度略有降低。
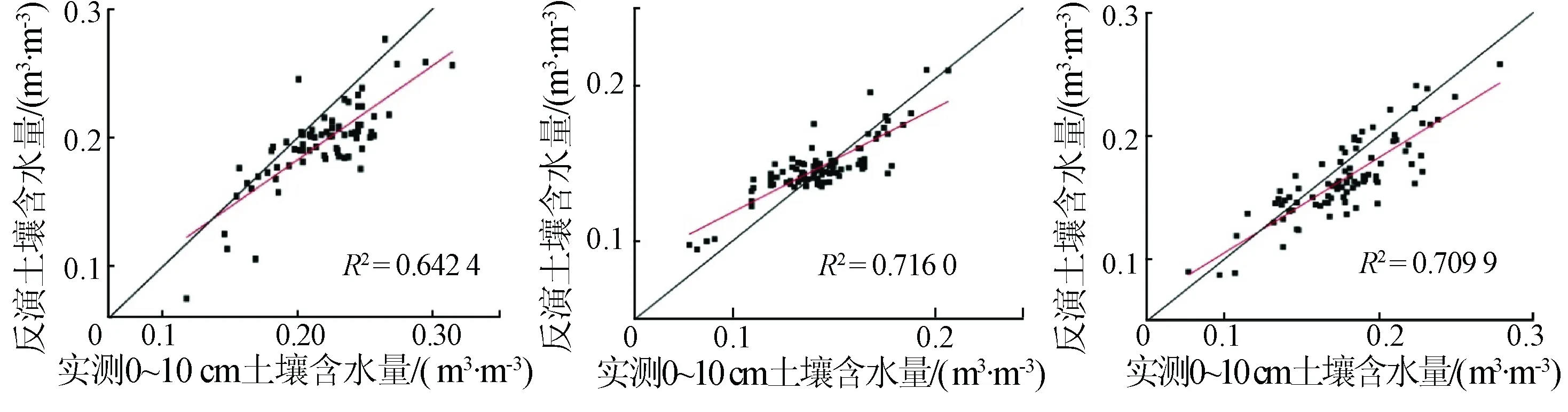
(a) 5月11日 (b) 5月21日 (c) 6月1日
图50~10cm实测土壤含水量与反演土壤含水量相关性分析
Fig.5Correlationanalysisofmeasured0~10cmsoilmoistureandestimatedsoilmoisture
图5为0~10 cm深度的实测站点土壤含水量与反演土壤含水量之间的线性回归分析结果。因为上文结果已经证实,遥感反演的土壤含水量与0~10 cm深度的实际土壤含水量关系比较密切,所以在此着重分析反演结果与0~10 cm深度土壤含水量的关系。图中红线是拟合的直线,黑线是斜率为1的辅助线,理论上,红线应该与黑线重合。红线在黑线下的部分说明反演的土壤含水量较实测值低估,红线在黑线上的部分说明反演的土壤含水量较实测值高估。由图5中的相关系数可以看出,3个实验日中,相关系数R2均在0.7左右,说明反演的土壤含水量结果是比较可靠的,可以用反演的土壤含水量来反应实际的土壤含水量情况。
4 结论与展望
本文基于MODIS数据与实测数据,反演了淮河流域的土壤含水量。该反演方法具有以下优点:
1)提出的CDI模型考虑了低植被覆盖区与高植被覆盖区的不同适用性特点,综合ATI和VSWI这2种模型来进行研究。CDI模型可适用于复杂的植被覆盖区域,相较使用单一的反演模型,反演精度将大大提高。
2)建立的CDI与实测土壤含水量转换模型,可对遥感反演的无量纲结果进行转换,从而得到真实的土壤含水量值。这对于土壤含水量的定量监测与分析有较大的意义。
经过精度验证,反演的土壤含水量与0~10 cm和10~20 cm深度土壤含水量的平均均方根误差分别为0.022 3和0.036 0,特别是与0~10 cm深度数据的相关性较高,R2在0.7左右,精度较好,可满足日常业务化监测需要,且简便快捷,具有较大的应用潜力。
本次实验中也存在一些误差,在2.3节建立相关模型时,选取的是2014年5月1日的样本数据,样本所选取的日期不同,可能会对数据的相关性结果产生影响,这也会对反演的精度造成影响。将来可考虑进行更多后续实验,以求获得具有更高精度、更高效率的土壤含水量成熟产品。
参考文献(References):
[1] Chen C F,Son N T,Chang L Y,et al.Monitoring of soil moisture variability in relation to rice cropping systems in the Vietnamese Mekong Delta using MODIS data[J].Applied Geography, 2011,31(2):463-475.
[2] 刘 敏,王亮亮,蔡秋鹏.FDR和TDR测定几种典型土壤含水量的对比分析[J].水利信息化,2016(6):32-36.
Liu M,Wang L L,Cai Q P.Compaveral typical soil’s water content measuring with FDR and TDR[J].Water Resources Informatization,2016(6):32-36.
[3] Wagner W,Hahn S,Kidd R,et al.The ASCAT soil moisture product:A review of its specifications,validation results,and emerging applications[J].Meteorologische Zeitschrift,2013,22(1):5-33.
[4] Jordan C F.Derivation of leaf-area index from quality of light on the forest floor[J].Ecology,1969,50(4):663-666.
[5] Kahle A B.A simple thermal model of the Earth’s surface for geologic mapping by remote sensing[J].Journal of Geophysical Research,1977,82(11):1673-1680.
[6] Price J C.Thermal inertia mapping:A new view of the earth[J].Journal of Geophysical Research,1977,82(18):2582-2590.
[7] Price J C.On the analysis of thermal infrared imagery:The limited utility of apparent thermal inertia[J].Remote Sensing of Environment,1985,18(1):59-73.
[8] Jackson R D,Pinter Jr P J.Detection of water stress in wheat by measurement of reflected solar and emitted thermal IR radiation[C]//Spectral Signatures of Objects in Remote Sensing.Versailles:Institut National de la Recherche Agronomique,1981:399-406.
[9] Carlson T N,Gillies R R,Perry E M.A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover[J].Remote Sensing Reviews,1994,9(1/2):161-173.
[10] Sandholt I,Rasmussen K,Andersen J.A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status[J].Remote Sensing of Environment,2002,79(2/3):213-224.
[11] 赵英时.遥感应用分析原理与方法[M].北京:科学出版社,2003.
Zhao Y S.Analysis Principle and Method of Remote Sensing Applications[M].Beijing:Science Press,2003.
[12] 郭月婷,徐建刚.基于模糊物元的淮河流域城市化与生态环境系统的耦合协调测度[J].应用生态学报,2013,24(5):1244-1252.
Guo Y T,Xu J G.Coupling coordination measurement of urbanization and eco-environment system in Huaihe River Basin of China based on fuzzy matter element theory[J].Chinese Journal of Applied Ecology,2013,24(5):1244-1252.
[13] 张 怡,何政伟,薛东剑.MODIS数据预处理方法[J].地理空间信息,2013,11(3):49-51.
Zhang Y,He Z W,Xue D J.Pre-processing method of MODIS data[J].Geospatial Information,2013,11(3):49-51.
[14] 刁 伟,孟令奎,张东映,等.MODIS数据在湖北旱情监测中的应用[J].水利信息化,2013(1):12-15.
Diao W,Meng L K,Zhang D Y,et al.Application of MODIS data on the drought monitoring of Hubei Province[J].Water Resources Informatization,2013(1):12-15.
[15] 申广荣,田国良.基于GIS的黄淮海平原旱灾遥感监测研究——作物缺水指数模型的实现[J].生态学报,2000,20(2):224-228.
Shen G R,Tian G L.Remote sensing monitoring of drought in Huanghe, Huaihe and Haihe Plain based on GIS:The calculation of crop water stress index model[J].Acta Ecologica Sinica,2000,20(2):224-228.
[16] 王鹏新,龚健雅,李小文.条件植被温度指数及其在干旱监测中的应用[J].武汉大学学报,2001,26(5):412-418.
Wang P X,Gong J Y,Li X W.Vegetation temperature condition index and its application for drought monitoring[J].Geomatics and Information Science of Wuhan University,2001,26(5):412-418.
[17] Nichol J E,Abbas S.Integration of remote sensing datasets for local scale assessment and prediction of drought[J].Science of the Total Environment,2015,505:503-507.
[18] Cai G Y,Du M Y,Liu Y.Regional drought monitoring and analyzing using MODIS data:A case study in Yunnan Province[C]//Proceedings of the 4th IFIP TC 12 Conference on Computer and Computing Technologies in Agriculture IV.Nanchang,China:Springer,2010:243-251.
[19] 宋荣杰.基于遥感的旱区土壤湿度反演方法研究[D].杨凌:西北农林科技大学,2013.
Song R J.Study on Soil Moisture Inversion Method Based on Remote Sensing[D].Yangling:Northwest A and F University,2013.
[20] 吴 黎,张有智,解文欢,等.改进的表观热惯量法反演土壤含水量[J].国土资源遥感,2013,25(1):44-49.doi:10.6046/gtzyyg.2013.01.08.
Wu L,Zhang Y Z,Xie W H,et al.The inversion of soil water content by the improved apparent thermal inertia[J].Remote Sensing for Land and Resources,2013,25(1):44-49.doi:10.6046/gtzyyg.2013.01.08.

