基于观测角信息的HJ-1A/B卫星光学影像几何精纠正
杨 亮, 贾 益, 江万寿, 张 过
(1.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079; 2.长光卫星技术有限公司,长春 130000)
0 引言
虽然环境一号(HJ-1)A/B星已发射近9 a,但其存档的海量CCD影像并未得到充分利用,几何定位不准确及山区地形畸变误差是限制其应用的主要瓶颈之一。针对这一大规模数据的应用需求,中科院遥感所、武汉大学等单位已经研制了环境卫星影像几何精纠正系统,采用全球ETM+影像作为参考数据进行自动处理[1-4]。
目前,环境卫星对外提供的标准产品是二级影像产品,因为未消除地形起伏的影响,给后续的变化检测、定量遥感等应用带来了很大的麻烦,需要进一步做几何精纠正处理[1-6]。现有的二级影像数据几何精纠正方法可分为2种: ①假设可以通过影像匹配获取大量的可靠控制点,采用多项式拟合[2]或小面元[3-6]进行影像几何配准纠正; ②沿袭一级影像纠正的思路,先利用分布均匀且具有较好高程范围的控制点建立一个近似的成像模型(如直接线性变换模型[6]或仿射变换模型[7-8]),再进行正射纠正。其中,第1种方法的多项式模型无法表达地形起伏引起的畸变,三角面元的方法则需要大量分布均匀的控制点以反映地形的变化[7],因而无法适应控制点难以大量获取和地形起伏较大地区的影像精纠正要求; 第2种方法在理论上比较合理,但也需要均匀分布的三维控制点,难以普遍使用。因此,对于全球规模的定量遥感而言,急需寻找一种能适合于全球不同地区的影像精纠正方法。
在“863”项目“星机地综合定量遥感系统与应用示范”几何归一化子课题研究中,笔者注意到中低空间分辨率的遥感影像数据产品一般都附带有与影像对应的卫星观测角文件,该文件实际隐含了原始影像的成像模型信息,却没有被充分利用。针对这一情况,本文提出一种利用观测角信息重建CCD二级影像“成像模型”的方法,并利用90 m数字高程模型(digital elevation model,DEM)数据进行正射纠正。
1 常用几何纠正模型分析与对比
在卫星光学影像的几何纠正过程中,需要建立影像的行列号与对应地面点之间的数学关系,然后利用该数学关系确定纠正影像的像元在原始影像中的位置,最后进行灰度重采样,计算该点的像元值赋给纠正影像。除采用共线方程的严格模型外,常用的几何纠正模型包括仿射变换模型、多项式变换模型、直接线性变换(direct liner transformation,DLT)模型和有理函数模型(rational polynomial coefficient, RPC)[8-14]。其中,DLT模型和RPC模型可用于对多线阵共线方程进行近似,而仿射变换模型和多项式变换模型可用于影像配准或对DLT模型和RPC模型进行像方改正。
1.1 像方改正/影像配准模型
1.1.1 二维仿射变换模型
二维仿射变换模型将二维控制点与二维影像点以一种最简单的数学关系表示出来,由于需要的控制点少,所以在影像几何纠正中经常被采用。但该模型没有考虑高程引起的变形,因此不能用于卫星影像倾角较大或地形起伏较明显的情况。目前,该模型在有严格模型或替代模型的情况下,常用于像方改正,即
(1)
式中: (x,y)为影像像元坐标; (X,Y)为控制点坐标(一般为参考影像坐标);ki(i=1,2,…,6)为系数。
1.1.2 二维多项式变换模型
与仿射变换模型相比,多项式变换模型能改正影像的平移、旋转、缩放和扭曲等全局变形,在基于影像配准的几何纠正中经常被采用; 其缺点是无法表达地形起伏变形等局部突变。其数学表达式为

(2)

1.2 近似成像模型
1.2.1 扩展仿射变换模型
扩展仿射变换模型考虑了地形的影响[8-9],适合于视场角较小、近似平行投影的情况。由于需要拟合高程起伏的影响,对控制点的高程取值范围有一定的要求。其数学表达式为

(3)

1.2.2 扩展DLT模型
与扩展仿射变换模型类似,DLT模型将影像的像元坐标与地面点的坐标进行直接对应[6]。为了更好地适应大角度多线阵投影,可将分母相同的DLT模型扩展为分母不同的DLT模型,其数学表达式可表示为

(4)
式中Li(i=1,2,…,14)为系数。
该模型对控制点的高程变化有一定的要求,但与扩展仿射变换模型相比,DLT模型可以适应视场角更大的情况。
1.2.3 RPC模型
RPC模型[10]将地面点的三维坐标(P,L,H)与影像的行列号(l,s)以比值多项式的形式联系起来。RPC模型的表达式为

(5)
式中Nl,Dl,Ns,Ds分别为4个三次多项式,即
(6)
(7)
(8)
(9)
式中: (l,s)为去中心归一化的控制点影像行列号; (P,L,H)为去中心归一化的控制点地理坐标;ai,bi,ci和di(i=1,2,...,20)为模型的系数。
因为系数过多,RPC模型主要作为严格模型的替代模型使用,一般不宜利用地面控制点进行拟合。在用于影像纠正时,RPC模型常与像方改正模型配合使用,可利用控制点进一步拟合像方光学畸变和姿态变化等误差。
2 基于观测角信息的成像模型拟合
2.1 影像几何误差来源分析
环境卫星二级影像已经过系统几何纠正和相对辐射校正,镜头畸变、传感器平台位置与姿态的变化以及地球曲率对影像的影响可以忽略不计[2],但地形起伏在CCD影像中引起的畸变却不能忽略不计,由于采用双CCD相机拼接对地成像,较大的地形起伏在双拼相机的影像外侧会产生很大的畸变。影像成像时的传感器天顶角和方位角及与地形起伏的关系如图1所示。
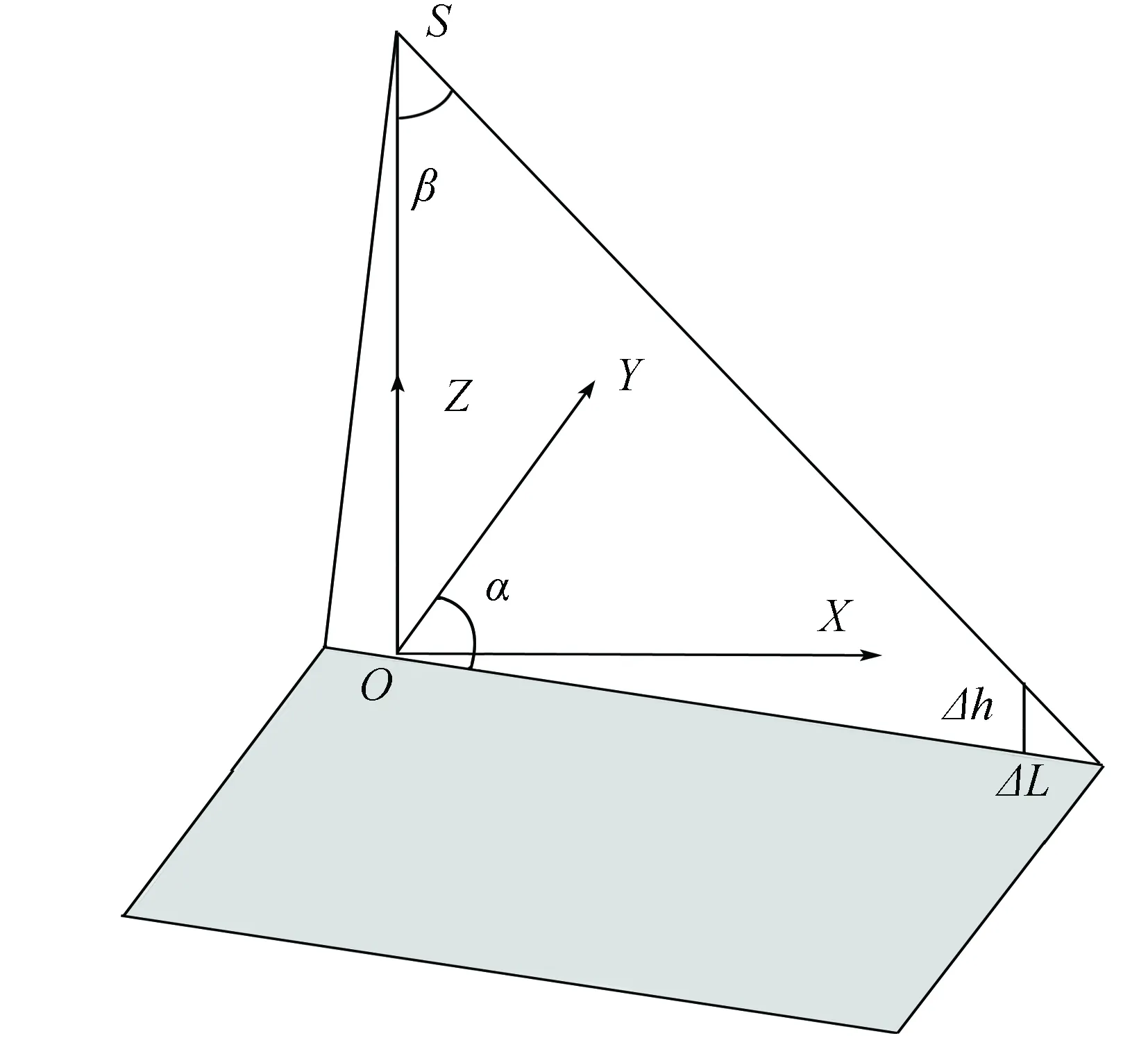
图1 影像的观测角与高程起伏引起的畸变
图1中,S为影像的投影中心,β为影像的传感器天顶角,α为传感器方位角。其中,β最大可达35°。根据几何关系可知,高程起伏Δh在影像上引起的畸变ΔL为

(10)
在影像最外侧,100 m地形起伏引起的影像畸变可达57 m,换算到像方达到1.92个像元。因此,高差几km的地区影像畸变可达近20个像元。
2.2 基于观测角信息的近似成像模型
由于RPC模型解算简单,能够很好地逼近严格成像模型,故本文选择RPC模型来拟合成像模型,并用于环境卫星二级光学影像的进一步几何精纠正,以消除地形起伏引起的畸变。
该影像二级产品的卫星角度文件SatAngle.txt包含了传感器天顶角和方位角的信息。考虑到数据量的问题,SatAngle.txt中的角度信息是33像元×33像元间隔的采样数据。由图1可知,从每个采样点的角度信息可以恢复该点的原始光束。因此,对每个像元的光线在多个高程面进行采样,就可以获得RPC模型拟合需要的控制网(图2)。

图2 根据角度信息建立的RPC拟合空间控制格网
利用环境卫星二级产品自带的观测角信息对RPC系数进行求解的过程如下:
1)读取角度信息文件并计算每个抽样像元的投影坐标。设有m×n个抽样像元的角度记录,每一行记录了L1及L2影像中的行列坐标、椭球高为0时的像元经纬度坐标、传感器方位角和传感器高度角。选择通用横轴墨卡托投影作为投影坐标系,然后由经纬度计算高程为0时的投影坐标(X0,Y0)。
2)根据经纬度坐标,从全球1 km格网DEM估计影像范围内的最小高程Zmin和最大高程Zmax,并分为5个高程面,每层之间的间隔Δh为(Zmax-Zmin)/4,第i个高程面的高程为Zmin+iΔh,i=0,...,4。
3)对于每个高程面Zi,计算每个采样像元光线对应的投影坐标。由(X0,Y0)和式(11)可计算Zi对应的投影坐标(Xi,Yi),即
(11)
4)通过m×n×5个地面点坐标与m×n个二级影像像素坐标,解算模型参数[11]。
3 实验与分析
3.1 实验数据
为验证本文提出的基于观测角信息的中等空间分辨率卫星影像几何精纠正算法的精度,本文选取2景高程起伏较大地区的HJ-1A/B CCD影像进行实验。影像1为西藏西南部HJ-1A CCD1影像,拍摄时间为2015年5月28日,影像成像范围为E82.7°~87.8°,N28.3°~32.2°,影像大小为16 717像元×14 407像元,共4个波段,地面海拔范围为88~6 597 m,平均海拔为3 774 m; 影像2为河北省HJ-1B CCD1影像,拍摄时间为2016年1月25日,成像范围为E111.6°~ 117.2°,N36.4°~40.4°,影像大小为16 516像元×14 771像元,共4个波段,地面海拔范围为-2~2 836 m,平均海拔为995 m。
3.2 实验流程
为了对比本文方法的效果,本文设计了3个实验方案,对第2节介绍的像方改正方法和近似成像模型方法进行组合(图3)。

(a) 方案1和方案2 (b) 方案3
图33种实验方案流程
Fig.3Threeprocessingflowsofexperiments
方案1和方案2如图3(a)所示,采用全球ETM+作为参考影像,通过影像匹配获取控制点,然后解算变换参数。方案1是影像配准的思路,通过多项式拟合影像之间的变形进行纠正; 方案2在方案1的基础上增加高程信息,通过扩展DLT模型拟合高程的影响,然后采用正射纠正的方式进行纠正。如图3(b)所示,方案3直接利用卫星观测角信息拟合成像模型,然后利用拟合得到的成像模型和90 m空间分辨率的DEM将参考影像模拟到影像成像时的大致状态,以消除姿态和高程起伏等引起的畸变,最后与影像进行匹配。
实验中先采用自动匹配的方法在30像元×30像元的规则格网上自动匹配控制点,然后通过粗差剔除和人工检查得到最终的控制点。为便于对比分析,不同方案采用统一的控制点,参数解算中不再自动剔除控制点。
3.3 结果与分析
像方改正采用仿射变换、二次多项式和三次多项式进行实验。分别对一次多项式、二次多项式和三次多项式进行了RPC参数拟合实验,发现一次多项式拟合误差较大,但不影响最终纠正结果; 二次多项式拟合精度最好,纠正精度最佳; 三次多项式可能存在过拟合,导致最终纠正误差很大。限于篇幅,像方改正只保留二次多项式和三次多项式的结果,RPC拟合只保留二次多项式结果。
影像1经匹配得到589个控制点,未经人工编辑,全部参与计算,控制点的行方向误差如图4所示,不同纠正方案的精度结果如表1所示。

(a) 三次多项式拟合误差 (b) 扩展DLT+二次多项式拟合误差
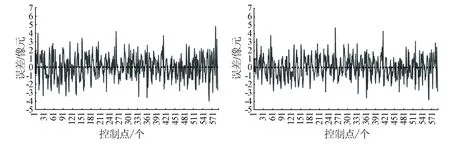
(c) 扩展DLT+三次多项式拟合误差 (d) 二次RPC+三次多项式拟合误差

图4 不同纠正方法结果的行方向误差曲线Fig.4 Error curves in line direction yielded by different rectification methods表1 影像1纠正误差Tab.1 Rectification error of image 1 (像元)
①mx和my分别为纠正影像在行方向和列方向的中误差; ② maxVx和maxVy为纠正影像在行方向和列方向的最大绝对误差。
从图4和表1可以看出,未考虑高程影响的多项式纠正影像在行方向存在多达20个像元的误差,在列方向误差相对较小,整个误差曲线不均衡; 考虑高程影响的正射纠正结果在行方向的误差减小到和列方向相当,列方向的误差也较未考虑高程影响的方案有较大的减小。采用二次多项式的误差曲线在列方向呈现明显的系统性; 采用三次多项式的误差比采用二次多项式的误差有较大的减小,且基本消除了列方向的系统性。对比由观测角文件重建RPC模型和控制点拟合DLT的纠正结果可以看出,两者的中误差和最大绝对误差比较接近,但是由观测角文件重建的RPC模型在行方向精度更高,大多数点的误差均在2个像素以内。
影像2经匹配共得到373个控制点,因参考影像和HJ-1B影像差异很大,对匹配点进行了人工检查和编辑。与影像1的实验结果类似,考虑高程的纠正结果能够很好地消除地形起伏的影响。可能由于增加了人工控制点编辑,减少了自动匹配控制点存在的误差,本景影像几何纠正的中误差和最大绝对误差都有较大幅度的减小(表2)。

表2 影像2纠正误差Tab.2 Rectification error of image 2 (像元)
4 结论
针对常规中等空间分辨卫星影像的几何纠正方法无法适应地形起伏较大区域的问题,提出了一种基于观测角信息的环境卫星CCD影像几何精纠正方法。该方法利用观测角信息重建影像的“成像模型”并用RPC模型表示,从而可以采用正射纠正的方法对二级影像进行正射纠正。实验证明,该方法无需控制点信息即可重建环境卫星光学二级影像坐标与地面坐标的关系,用于正射纠正的精度明显高于多项式法,并略优于DLT拟合法。该方法的最大优势在于重建成像模型过程不需参考影像及其控制点,不受控制点平面分布及高程分布的影响,具有较大的普适性。
参考文献(References):
[1] 唐 娉,张宏伟,赵永超,等.全球30 m分辨率多光谱影像数据自动化处理的实践与思考[J].遥感学报,2014,18(2):231-253.
Tang P,Zhang H W,Zhao Y C,et al.Practice and thoughts of the automatic processing of multispectral images with 30 m spatial resolution on the global scale[J].Journal of Remote Sensing,2014,18(2):231-253.
[2] 熊文成,申文明,王 桥,等.环境一号卫星A/B星数据自动几何精校正设计研究[J].中国工程科学,2014,16(3):37-42.
Xiong W C,Shen W M,Wang Q,et al.Research on HJ-1A/B satellites data automatic geometric precision correction design[J].Engineering Science,2014,16(3):37-42.
[3] 唐 亮,唐 娉,阎福礼,等.HJ-1 CCD图像自动几何精纠正系统的设计与实现[J].计算机应用,2012,32(s2):237-241.
Tang L,Tang P,Yan F L,et al.Design and implementation of automatic accurate geometric correction system for HJ-1 CCD images[J].Journal of Computer Applications,2012,32(s2):237-241.
[4] 单小军,唐 娉,胡昌苗,等.图像分层匹配的HJ-1A/B CCD影像自动几何精校正技术与系统实现[J].遥感学报,2014,18(2):254-266.
Shan X J,Tang P,Hu C M,et al.Automatic geometric precise correction technology and system based on hierarchical image matching for HJ-1A/B CCD images[J].Journal of Remote Sensing,2014,18(2):254-266.
[5] 胡九超,周忠发.基于快速匹配与线性橡皮拉伸的HJ-1CCD影像几何精校正[J].湖北农业科学,2015,54(3):703-704,708.
Hu J C,Zhou Z F.HJ-1CCD image geometric accurate rectification based on fast matching and linear rubber sheeting[J].Hubei Agricultural Sciences,2015,54(3):703-704,708.
[6] 李全文,赵卫林,杨晓梅,等.基于FAST测点的大幅宽HJ星图像几何精纠正方法[J].国土资源遥感,2014,26(4):14-22.doi:10.6046/gtzyyg.2014.04.03.
Li Q W,Zhao W L,Yang X M,et al. AST algorithm-based geometric accurate rectification of large HJ satellite image[J].Remote Sensing for Land and Resources,2014,26(4):14-22.doi:10.6046/gtzyyg.2014.04.03.
[7] 潘建平,郝建明,赵继萍.基于SURF的图像配准改进算法[J].国土资源遥感,2017,29(1):110-115.doi:10.6046/gtzyyg.2017.01.17.
Pang J P,Hao J M,Zhao J P.Improved algorithm based on SURF for image registration[J].Remote Sensing for Land and Resources,2017,29(1):110-115.doi:10.6046/gtzyyg.2017.01.17.
[8] Savopol F,Armenakis C.Modelling of the IRS-1C satellite pan stereo-imagery using the DLT approach[C]//Proceedings of 1998 IAPRS Commission IV Symposium on GIS-Between Visions and Applications,Stuttgart:[s.n.],1998:511-514.
[9] Hattori S,Ono T,Raser C F,et al.Orientation of high-resolution satellite images based on affine projection[C]//Proceedings of International Archives of Photogrammetry and Remote Sensing.Amsterdam: ISPRS,2000:359-366.
[10] 张剑清,张祖勋.高分辨率遥感影像基于仿射变换的严格几何模型[J].武汉大学学报(信息科学版),2002,27(6):555-559.
Zhang J Q,Zhang Z X.Strict geometric model based on affine transformation for remote sensing image with high resolution[J].Geomatics and Information Science of Wuhan University,2002,27(6):555-559.
[11] Tao C V,Hu Y.A comprehensive study of the rational function model for photogrammetric processing[J].Photogrammetric Engineering and Remote Sensing,2001,67(12):1347-1357.
[12] 张 过,李 扬,祝小勇,等.有理函数模型在光学卫星影像几何纠正中的应用[J].航天返回与遥感,2010,31(4):51-57.
Zhang G,Li Y,Zhu X Y,et al.Application of RFM in geometric rectification of optical satellite image[J].Spacecraft Recovery and Remote Sensing,2010,31(4):51-57.
[13] 巩丹超,张永生.有理函数模型的解算与应用[J].测绘学院学报,2003,20(1):39-42,46.
Gong D C,Zhang Y S.The solving and application of rational function model[J].Journal of Institute of Surveying and Mapping,2003,20(1):39-42,46.
[14] 杨宝林,吕婷婷,王少军,等.Pleiades卫星图像正射纠正方法[J].国土资源遥感,2015,27(3):25-29.doi:10.6046/gtzyyg.2015.03.05.
Yang B L,Lyu T T,Wang S J,et al. Ortho-rectification method for Pleiades satellite images[J].Remote Sensing for Land and Resources,2015,27(3):25-29.doi:10.6046/gtzyyg.2015.03.05.

