MGO软件在地下水污染抽出-处理方案优化中的应用
, ,,,
(1.南京大学地球科学与工程学院,江苏 南京 210023;2.南京水利科学研究院, 江苏 南京 210029)
随着工业化的发展加速,地下水污染问题日益突出,极大地破坏着生态环境并威胁着民众的健康[1-3]。根据污染物种类和含水层类型的不同,有多种不同的地下水污染治理与修复方法[4],其中基于水力控制的污染物抽出-处理(pump and treat, PAT)技术最为典型。其主要优点在于简便易行,可对地下水污染事件做出快速反应,尤其适用于期望短期内迅速降低污染水平的地下水水源地含水层系统,缺点在于修复工程复杂、且运行成本高昂。因此,有效降低PAT系统的运行成本对于该技术的推广应用具有重要意义。自20世纪80年代以来,地下水模拟-优化模型就应用于确定地下水PAT系统的最优策略[5]。然而,与国内外广泛存在的模块化地下水模拟软件相比,地下水模拟-优化模型方面的研究虽然很多[6-9],但模块化的模拟-优化软件相对很少,这种状况极大地限制了地下水模拟-优化模型在实际场地中地下水污染治理的优化实践。
MGO(Modular Groundwater Optimizer)[10]是一款模块化的地下水模拟优化软件,它通过耦合地下水水流模型MODFLOW[11]和污染物运移模型MT3DMS[12]结合通用管理目标建立地下水PAT系统的模拟-优化模型,并可根据需要选择不同优化算法对模型进行求解。本文基于MGO软件,运用遗传算法对美国犹他州的某地下水污染场地进行抽出-处理系统的优化研究,确定抽水井群的单井最优动态抽水量,实现以最低的系统运行成本达到修复含水层的最优目标。
1 MGO软件简介
MGO(Modular Groundwater Optimizer)是美国阿拉巴马大学教授Zheng和Wang基于地下水水流模型MODFLOW和污染物运移模型MT3DMS 开发出来的一款针对地下水PAT系统优化的通用模块化优化管理软件。利用MGO不仅能建立完全耦合地下水模拟模型(包括水流模型和运移模型)的嵌入式模拟-优化模型,而且对于特别复杂的地下水优化问题还能结合实际情况建立新的基于替代模型(或响应函数)的地下水模拟-优化模型。无论是嵌入式优化模型还是基于响应函数的优化模型,MGO都可选择遗传算法(GA)、模拟退火(SA)和禁忌搜索(TS)等多种进化算法中的任一算法来求解,从而保证能找到复杂地下水非线性模拟-优化问题的最优解。
MGO既能应用于地下水系统的单一水量/水质优化管理,也能应用于水量与水质的联合优化管理,尤其适用于基于水力控制的地下水污染治理的PAT系统中的抽注水方案优化管理。同时,MGO采用模块化设计(见图1),能直接利用地下水模拟模型MODFLOW和MT3DMS中的输入文件,大大简化了软件的使用,便于推广应用。

图1 MGO代码设计流程图
2 基于MGO的地下水PAT系统模拟-优化模型
为了能同时考虑各种不同的水量/水质优化管理问题,基于MGO设计的地下水PAT系统优化模型可表示为以下通用数学形式[10]:
目标函数:
(1)
约束条件:

(2)
Qmin≤Qi≤Qmax
(3)
hmin≤hm≤hmax
(4)
(5)
cmin≤cm≤cmax
(6)

(7)
上述优化模型中,式(1)为通用目标函数,J是管理目标,可以是总成本、总抽水量或含水层中污染物的总去除量等。用户可以根据实际情况选取目标函数右端项中的一项或若干项(亦可表示为最大化)。Qi是某个管理期内的第i个井在单位时间内的抽/注水量,正值代表注水、负值代表抽水。对于单个管理期优化问题,任何井的抽/注水量均为是常数,只需用一个参数表示;而对于多管理期的优化问题,由于任何一个井在不同管理期的抽/注水量可以不同,则需要多个参数来表示井在不同管理期的抽/注水量。Mi第i井的溶质移除量。F(q, h, c)用户自定义成本函数,可以依赖于流量q,水头h,浓度c。N是待优化参数的总数目,下同。yi是个二进制数,当考虑参数i活跃时,yi=1;否则yi=0。di是第i参数相关的井径深度。Δti是参数i的抽/注水持续时长期。α1每个井的固定资产成本。α2是井筒单位深度的安装、打钻成本。α3是单位体积的抽水和处理成本。α4是单位质量污染物的处理成本。α5是外部用户指定的成本系数。
式(2)-(7)为通用约束条件。式(2)要求任何时间段内的决策井数目不得超过一个给定的约束值(NW)。 式(3)是对任一管理期内单位时间的抽水量约束,Qmin、Qmax分别是对应井的最小、最大单位抽水量。式(4)是水头约束,hm是监测点位置的水头,hmin、hmax分别是其最小、最大约束水头。式(5)是水力约束,Δhmin是外部监测点与内部监测点之间所允许的最小水头差。式(6)是浓度约束,cm是任一监测点的浓度,cmin、cmax是该监测点的最小、最大浓度允许值。式(7)可作为均衡约束,Qm是与从井I1到井I2的抽/注水量之和成比例的抽水量,其中A、B为比例系数。同样地,用户可以根据优化模型中目标函数的组成来确定和选择必要的约束条件。
优化模型中涉及到两种变量:决策变量和状态变量。决策变量包括抽/注水井的数量、位置和流量;状态变量就是指地下水的水位和污染物的浓度。水位和浓度状态变量对应于决策变量的响应分别由水流模型MODFLOW和溶质运移模型MT3DMS来获得更新。因此,对于嵌入式模拟-优化模型来说,采用进化算法求解时,都要针对决策变量(井流量、井位等)不断重复调用水流模型MODFLOW与溶质运移模型MT3DMS来计算相应的状态变量(水位、浓度),由此进一步计算目标函数值并判断约束条件是否满足,从而搜索得到模型的最优策略。

图2 研究区场地位置及模型第1层的初始TCE污染羽分布
3 实例应用
3.1 污染场地概述与模拟-优化模型
3.1.1 场地概述及模拟模型
研究场址位于美国犹他州大盐湖以南约10 km的图埃尔(Tooele)山谷。含水层主要由冲积层构成,但在其中部有一向上抬升的基岩块,使地下水从冲积沉积物中流向断裂风化的基岩,然后又回到冲积沉积物中。区域地下水流大致向东南往西北方向流动。场地主要污染来自于其东南角的一个工业区,主要污染物为TCE。监测结果表明,污染物主要分布在含水层的浅部,但由于场地地下水流的复杂性,浅部污染羽和深部污染羽的范围并不一致,甚至东北角的污染羽已延伸到特征边界之外(见图2)。
现已确定采用基于水力技术的抽出-处理技术来治理和修复该含水层,该PAT系统由美国某陆军工程兵团设计,包含16口抽水井、13口注水井和1口附加抽水井(E-fixed)。相应的模拟模型已实现了抽水/不抽水条件下的多次校正,该模型是一个三维、稳态的MODFLOW模型,有4层,165行,和99列。平面上剖分为正方形单元网格,其边长为60.96 m,垂向上自上而下4个模型层的平均厚度分别为45.72 m、30.48 m、45.72和91.44 m。基于MT3DMS构建与之对应的污染物运移模型。模型时间离散化为有7个3年的应力期来匹配优化方案中定义的管理期。
现以校正后的模拟模型计算出的2003年1月的水头分布与污染羽分布分别作为初始水头、初始浓度分布。由于现存PAT系统模拟结果显示,没有可行解能满足污染羽截断边界的约束条件。经过前期的专家论证,需新增4口注水井(IN1~IN4),原有PAT系统中的16口抽水井、13口注水井和1口附加抽水井(E-fixed),仅需保留抽水井E11和E15、注水井I4及E-fixed,但E11和E15均以最大抽水能力运行,各井位置见图2。需要说明的是,为了维持PAT系统的稳定性,所有抽水井与注水井的水量总量相等。
3.1.2 优化模型及其求解
本文在确定了井的位置基础上,令每一个管理期的所有注/抽水井(E-fixed与I4除外)的流量为一个决策变量,以制定出一种最优的动态解。选择使用GA进行最优解的搜索,相关的参数设置如下:POPSIZE=200,PCROSS=0.5, PMUTATE=0.05,NPOSIBL=32。
根据目标函数的一般形式,由于井位、井数已定,总成本项主要来自抽水用电成本项和化学处理项,其中本文把抽水用电成本项当作安装成本,调整后的通用目标函数可简化为如下PAT系统的最小运行成本:
(8)
相应的约束条件如下:
|Qsumin|≤|Q*|≤|Qsumax|
(9)
(10)
QI4=-(QEi+QNIi)-QE-fixed
(11)
Cm≤Cmax
(12)
0≤QEi≤│Li│
(13)
0≤QNIi≤Li
(14)
式(8)中,α1取值为34.5K$(1K$表示1 000美元),α3取值为1.01e-05K$/(m3);M表示管理期,M=7;N=6;yji是二进制数,当第j管理期新建或优化第i个井时,yji=1,否则yji=0。式(9)、(10)都作为全局约束条件:其中式(9)是对总抽水量的约束;Q*是参与模拟的总抽水量(包括E-fixed的抽水量),Qsumax为最大总抽水量,取值为-41 427.42 m3/d,Qsumin为最小总抽水量,取值为0;式(10)是对抽/注水量和的约束,Qi为参与模拟的第i个井的抽/注水量,i=1,2,…,8;Qc为最大均衡误差值,取值为5.45 m3/d。NW为各管理期参与模拟的井数,本次优化各管理期NW均取值为8。式(11)作为均衡约束条件:QI4是现用注水井I4的注水量;QEi是第i个现用抽水井的抽水量,i=1,2;QNIi是第i个新建注水井的注水量,i=1,2,3,4;QE-fixed是E-fixed的抽水量,值为-7 767.68 m3/d。式(12)为浓度约束条件:Cm是第m个浓度约束边界单元上TCE的浓度值,Cmax为不同管理期末的约束浓度上限,取值为5 μg/L。式(13)、(14)分别为现用井的抽/注水量、新建注水井的注水量的约束条件:QEi为第i个现存井的抽/注水量,i=1, 2, 3,Li为第i个井的最大抽/注水能力。PAT系统中参与优化的井的最大抽/注水能力如表1所示。
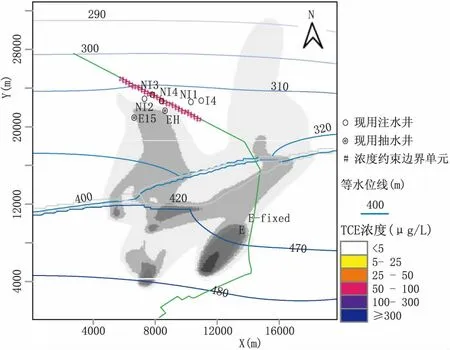
图3 执行最优策略最终管理期末得到模型第1层中的污染羽分布

图4 执行最优策略最终管理期末得到模型第2层中的污染羽分布表1 优化前PAT系统中待优化抽/注水井的抽/注水能力及其模拟层

井Li/m3/d模拟层E11-3 365.992E15-3 314.212, 3I44 163.472IN13 107.071IN23 107.072IN33 107.071IN43 107.071
如表1所示,抽水井E15抽采2、3两层,因此只要以其第2层的抽水量作为决策变量,而将第3层的抽水量处理为依赖变量,抽水量的分配依据两层的导水系数可由优化程序自动计算得到。
3.2 优化结果与分析
最优抽水策略满足所有约束条件,包括在4个模拟层的污染约束边界单元处,污染羽浓度在每个管理期末均接近或小于5 μg/L。第1、2含水层是污染物主要分布层,这两层在第7个管理期的污染羽分布见图3和图4。动态策略下各管理期的抽/注水量见图5、表2。原稳态策略下的抽/注水量同见图5。
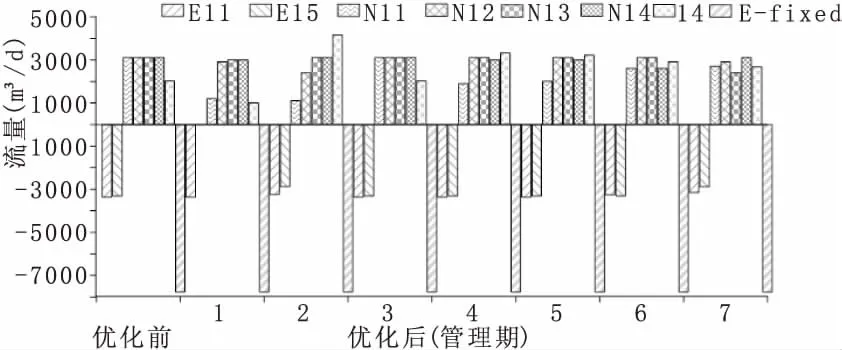
图5 最优策略下各管理期的抽水(负值)/注水(正值)量分布表2 动态策略下各管理期内优化得到PAT系统的抽水(负值)和注水(正值)方案

井号优化前优化后管理期抽/注水量/m3/d1234567E11-3 365.99-3 365.99-3 245.85-3 365.99-3 365.99-3 365.99-3 257.14-3 149.81E15-3 314.210-2 876.33-3 314.21-3 314.21-3 314.21-3 314.21-2 886.52NI13 107.071 202.871 109.663 107.071 904.3072 004.552 606.012 706.20NI23 107.072 906.852 407.983 107.073 107.073 107.073 107.072 906.85NI33 107.073 005.743 107.073 107.073 107.073 107.073 107.072 405.42NI43 107.073 005.743 107.073 107.073 005.743 005.742 606.013 107.07I42 019.601 010.784 158.302 019.543 322.113 223.232 912.522 677.75
优化后的动态策略抽水井E15在第1管理期内抽水量为零,并且在第2、第7管理期内低于最大负荷抽水率运行,在整个项目期内抽水井E15抽水量相比优化前减少了18.02%,抽水井E11在第2、6、7管理期也是低于最大抽水量运行,项目期内抽水井E11的抽水量减少了1.89%,管理期的总抽水量减小了9.89%,此外,抽注水量之和小于给定最大值5.45 m3/d,说明来自三口抽水井的抽水量都从5口注水井注入含水层中。因此动态策略下整个项目期的总抽水量减小,使得抽水用电成本和化学处理成本相应减少。
在稳定策略下,总成本为1 258.85K$,其 中抽水用电成本、化学处理成本各占73.79%、26.21%。而优化后动态策略下抽水用电成本相比优化前减少10.62%;化学处理成本相比优化前减少13.08%。总成本为1 117.02K$,相比优化前总成本减少了11.27%。
4 结语
本文通过MGO软件对美国犹他州某处TCE污染场地的PAT修复系统进行模拟优化管理,实现了对修复系统的动态优化管理。优化结果表明优化后的修复策略减少了11.27%的修复成本,同时保证了修复效率。实例研究的结果表明MGO可以有效地为地下水修复提高经济、高效的管理措施,为今后的地下水污染修复提供一种可靠的工具,具有较好的应用前景。
[1]吕书君. 我国地下水污染分析[J]. 地下水.2009.31(1): 1-5.
[2]Soderstrom M, Boldemann C, Sahlin U, et al. The quality of the outdoor environment influences childrens health-across-sectional study of preschools. Acta Paediatrica, 2013.102: 83-91.
[3]Ozdemir S, Johnson FR. Estimating willingness to pay: do health and environmental researchers have different methodological standards Applied Economics, 2013.45: 2215-2229.
[4]李玮,王明玉,韩占涛,等. 棕地地下水污染修复技术筛选方法研究—以某废弃化工厂污染场地为例[J]. 水文地质工程地质.2016.43(3): 131-141.
[5]Minsker BS editor. Long-Term Groundwater Monitoring: The State of the Art[M]. ASCE/EWRI, 0-7844-0678-2, Reston, VA; 2003.
[6]肖传宁,卢文喜,安永凯,等. 基于两种耦合方法的模拟-优化模型在地下水污染源识别中的对比[J]. 中国环境科学.2015.35(8): 2393-2399.
[7]吴剑锋,彭伟, 钱家忠, 等. 基于INPGA的地下水污染治理多目标优化管理模型:I—理论方法与算例验证[J]. 地质评论.2011.57(2): 277-283.
[8]吴剑锋,彭伟, 钱家忠, 等. 基于INPGA的地下水污染治理多目标优化管理模型: II.实例应用[J]. 地质评论.2011.57(3): 1-7.
[9]Zhang JL, Li YP, Huang GH. A robust simulation-optimization modeling system for effluent trading—a case study of nonpoint source pollution control[J]. Environmental Science and Pollution Research.2014.21: 5036-5053.
[10]Zheng C, Wang PP. MGO-A Modular Groundwater Optimizer Incorporating MODFLOW/MT3DMS, Documentation and User’s Guide[R]. The University of Alabama and Groundwater Research Ltd., Tuscaloosa, AL, 2003.
[11]McDonald MG, Harbaugh AW. A modular three-dimensional finite-difference groundwater flow model. Techniques of Water Resources Investigations of the U.S. Geological Survey, Book 6[R], U.S. Government Printing Office, Washington, D.C., 1988.
[12]Zheng C, Wang PP. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide, Contract Report SERDP-99-1[R]. U.S. Army Engineer Research and Development Center, Vicksburg, MS. 1999.

