应用整数小波变换的LZ77电力数据压缩算法

许晓飞，陈 亮

(西安工程大学 计算机科学学院,陕西 西安 710048)

0 引 言

电力系统的采样数据对分析电网运行状态、故障诊断、状态评估具有重要意义,保证这些电能量数据实时、准确地传递到调度中心主要的方法是对数据进行压缩．目前电力系统使用的数据压缩方法分为传统压缩算法和变换域的压缩方法[1]．传统的压缩算法包含自适应霍夫曼编码、算术编码、LZ系列编码等压缩算法．文献[2]为解决智能电网中大量数据远距离通信速率慢的问题,将动态自适应霍夫曼编码应用于电力系统测量数据压缩中,有效减少了数据传输时间,并将测量数据实时上传;文献[3]为提高电力采集数据的传输效率,使用LZ77算法对电能量和电能质量等长通信报文进行压缩,获得25%的压缩比,减少了80%的数据传输时间．应用变换域的数据压缩方法主要依据其良好的多分辨率分析的特性[4]得到了广泛的应用.文献[5-8]利用小波分解和重构的特性,直接采用小波变换对电力数据进行压缩．得到的压缩比为16%～30%,其原始信号和恢复信号的均方误差一般小于10-6～10-5．小波变换过程中的卷积运算由于小波系数滤波器普遍是浮点型影响了算法的实时性,因此,整数小波变换被运用到电力系统数据压缩中[9-11]．在同等数据长度条件下,应用整数小波变换与使用传统小波变换的压缩方法相比,不仅压缩速度提高了近1倍[12],而且可以实现无损压缩．

本文针对电力数据的特点以及小波变换后保留系数之间的相关性,提出一种应用整数小波变换的LZ77电能质量数据压缩算法．该算法依据整数小波变换的多分辨率分析特性,将原始电能量数据变换到小波域,对低频系数进行数据变换后用LZ77压缩算法处理,对高频系数选取门限进行阈值量化处理,得到相对更小的压缩比．

1 应用提升格式的小波滤波器组

1.1 经典小波滤波器组的提升原理

Sweldens提出的提升算法是一种简明有效地构造小波的方法,它经过分裂、预测以及更新3个步骤,逐步构建具有良好性质的小波．使用提升算法构建的小波不仅拥有经典小波的多分辨率分析特性、占用存储空间小等优点,并且在相同数据长度下,提升算法构建的小波使速度提高将近1倍[13]．因此,本文用提升算法实现经典小波滤波器组,并将之应用于实践．

若要使用提升算法实现经典小波滤波器组,建立提升算法构建的小波变换和经典小波滤波器组间的联系,首先要得到小波滤波器组的多相矩阵形式:

(1)

(2)

(3)

(4)

对he(z)和ho(z)进行多相位矩阵因子分解，得到

(5)

式(5)中K为刻度因子,(si(z),ti(z))两个罗朗多项式在之后分别用于构造第二代小波变换中的预测算子和更新算子．然后引入新矩阵P0(z)以推出P(z)的因子分解实现形式,

令

(6)

(7)

将式(1)和式(7)代入式(6)得到与h(z)互补的滤波器g0(z),再根据式(5)计算P0(z):

(8)

将式(8)代入式(7)确定g0(z),并由式(6)和式(7)计算原始提升系数sm(z):

(9)

联立式(6)，(8)，(9)得到式(1)，(2)经典小波的提升格式为

(10)

(11)

至此,经典小波变换利用因子分解方法完成了传统卷积模式的提升．以Bior4.4小波滤波器组为例,其提升实现正变换公式为

(12)

(13)

(14)

(15)

式中:α=-1.586 134 34,β=1.079 636 78,γ=-0.052 980 12,ε=-0.882 911 08,δ=0.443 506 85,η=1.576 123 75,K=-1.149 604 40.

1.2 整数小波变换

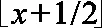
1.3 小波基选择

虽然对电力采集数据的压缩能够通过小波分解将原始数据中的不同数据分开,但是并不是所有的小波基函数都适用于电力数据的压缩．本文对比小波的正交性、对称性以及消失矩等方面选取Daubechies小波、双正交小波以及对称小波3种适合数据压缩的小波基,并通过数据对3类小波基在压缩中的性能效果进行对比,其仿真实验的统计结果如图1，2所示.

图 1 压缩比与分解层数关系 图 2 误差与分解层数关系Fig.1 Relationship of compression ratio and decomposition layer Fig.2 Relationship of error and decom-position layer

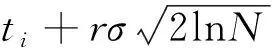
从图1可以看出，3种小波基的压缩比在分解层数为4层时最低;从图2可以看出，3种小波基在分解4层后误差基本保持不变;各小波基压缩效果比较见表1.从表1可以看出，在分解层数为4层时,Bior4.4小波基的压缩比为6.972 4%,能量恢复系数为99.502 4,略强于Db4和Sym4,对于光滑信号,双正交小波函数比Db小波函数系的逼近能力更好,而逼近能力越强,压缩比就越高．并且在进行小波变换时由于Bior4.4的对称性更好,相位失真小,所以重构信号时畸变也小．

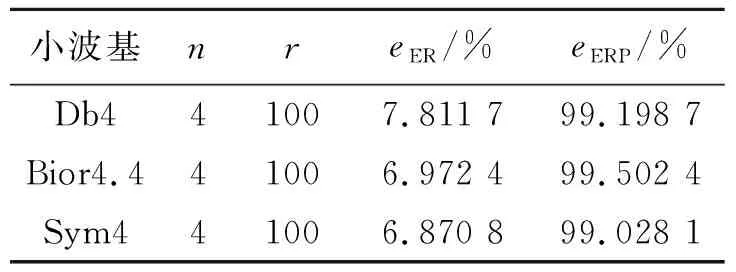
表 1 各小波基压缩效果比较

2 LZ77压缩算法

用小波分解和阈值处理电力数据后,大部分变为不被纳入存储数据的0,并且由于含有重要信息的低频分量是正弦信号,其数据是不断重复的、具有周期性的数据,而LZ77压缩算法是利用数据的重复结构信息压缩数据,适合这类数据．LZ77算法是应用字典模型的经典压缩算法,它的动态字典由字典窗口和先行缓冲区体现．LZ77将进入先行缓冲区的数据与字典窗口的数据进行比较,如有匹配则按规定的格式代码表示输入的数据,而经过匹配，编码的数据流成为字典的一部分．其算法及其流程见文献[15]．

3 数据压缩实验与讨论

3.1 压缩效果评价标准

对于压缩效果的性能评价标准,本文定义了相应的衡量指标:

(1) 压缩比是压缩后的数据容量Nc与原始数据容量N的比值．

eCR=Nc/N×100%.

(2) 能量恢复系数是评价压缩算法恢复能力的参数．

(3) 均方误差是误差评价标准．

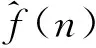
3.2 实验结果与分析

用整数小波变换对采样数据进行压缩,其效果与小波基的选择、小波分解层数、高频分量阈值的设置有关．实验中阈值系数都设为0.9,小于这个量化阈值的小波分量将被置零,采用提升后的Bior 4.4小波选取合适的小波分解层数来验证该算法的正确性和有效性．

原始数据采用如图3所示的电能量数据,该数据对50 Hz工频信号进行A相电压采样,采样频率为54 kHz,共采集5个周波,共计5 400个点．图4为重构后的电压数据,图5为原始电压数据与重构数据的差值,电压数据的压缩结果见表2,其中n为Bior 4.4小波的分解层数，eCR1是应用量化阈值的整体压缩比,eCR2是LZ77算法对低频系数的压缩比,eCR是算法的整体压缩比,eERP能量恢复系数;eMSE为均方误差值．

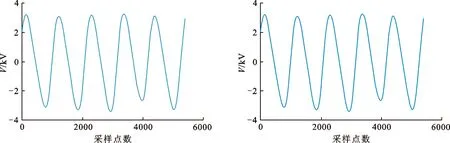
图 3 原始数据 图 4 重构数据 Fig.3 Original data Fig.4 Reconstructed data

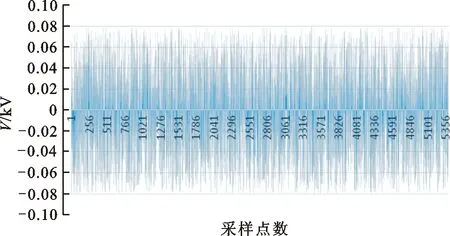
图 5 压缩前后差值数据Fig.5 Difference data before and after compression

neCR1eCR2eCReERPeMSE234.7932.7530.9599.2380.722319.7628.8724.9699.0611.724414.3825.0710.7698.9712.07857.5428.548.2498.0143.69463.8727.846.9697.7584.621

电压数据的压缩结果见表2.从表2可以看出,随着小波分解层次的加深,低频分量的压缩比和算法整体压缩比随之减少,但是随着分解层数的加大,高层尺度系数的数量开始逐半减少,用于重构数据的特征信号也相应减少,均方误差随之增大,减弱了算法的有效性,因此压缩比和均方误差是相互制约的．考虑到电力系统实时性和准确性的要求,所以小波分解层数不宜过高,均方误差不宜过大,本文选择Bior4.4小波,分解层数为4．原始电能量数据进行整数小波变换后,对高频分量进行阈值量化处理,对低频分量进行数据变换后再用LZ77算法压缩,不仅达到了10.76%的整体压缩比,且压缩后的数据保留了98.971%的频谱能量,均方误差为2.078%,压缩效果良好．

4 结 论

(1) 在小波变换的基础上,针对其浮点型数据做卷积运算耗时过多的问题,应用提升算法构造整数小波变换,使压缩速度提高;

(2) 通过电能质量数据的压缩比和能量恢复系数评判标准选择适合电能质量数据压缩的小波基;

(3) 对实际的电压数据进行仿真,比较分析各分解层数的压缩效果,双正交提升小波Bior4.4的分解层数为4层时,电能质量数据的压缩与重构的效果良好,实用价值高．

参考文献(References)：

[1] 王丽君.电力系统数据压缩传输的研究与实现[D].北京:北京化工大学,2010:2-4.

WANG L J.Research and implementation of data compression and transmission in power system[D].Beijing:Beijing University of Chemical Technology,2010:2-4.

[2] 张敬敬,朱永利,郝宁.Huffman压缩算法在智能电网通信系统中的应用[J].河北工业科技,2010,27(6):473-476.

ZHANG J J,ZHU Y L,HAO N.Application of huffman compression algorithm in smart grid communication systems[J].Hebei Journal Industrial Science and Technology,2010,27(6):473-476.

[3] 池智伟,张颖,郑州.数据压缩在用电信息采集远程通信中的应用[J].电力信息与通信技术,2013,11(4):39-45.

CHI Z W,ZHANG Y,ZHENG Z.Application of data compression in telecommunication information acquisition remote communication[J].Electric Power Information and Communication Technology,2013,11(4):39-45.

[4] DAUBECHIES I.Ten lectures on wavelets[M].Society For Industrial And Applied Mathematics.Philad elphia,Pennsylvania,1992:16-40.

[5] 欧阳森,宋政湘,陈德桂,等.基于小波原理的电能质量检测数据实时压缩方法[J].电网技术,2003,27(2):37-40.

OUYANG S,SONG Z X,CHEN D G,et al.A wavelet theory based real-time data compression method for power quality detection[J].Power System Technology,2003,27(2):37-40.

[6] 康忠健,樊建川,徐丽.自适应小波压缩算法在连续录波装置中应用[J].电力自动化设备,2009,29(10):116-119.

KANG Z J,FAN J C,XU L.Application of adaptive wavelet data compression algorithm in continuous recorder[J].Electric Power Automation Equipment,2009,29(10):116-119.

[7] 剧高峰,罗安.离散小波变换用于电能质量扰动数据实时压缩[J].电力系统自动化,2002,26(19):61-63.

JU G F,LUO A.DWT application to real-time compression of power quality disturbance data[J].Automation of Electric Power Systems,2002,26(19):61-63.

[8] 何正友,钱清泉,刘志刚.一种基于优化小波基的电力系统故障暂态数据压缩方法[J].中国电机工程学报,2002,22(6):1-5.

HE Z Y,QAIN Q Q,LIU Z G.An electric power system fault transient data compression method based on optimized wavelet[J].Proceedings of the CSEE,2002,22(6):1-5.

[9] 黄天戍,汪阳,吴迪,等.基于第二代小波变换的电力系统故障录波数据压缩方法[J].电力自动化设备,2004,24(3):59-62.

HUANG T S,WANG Y,WU D,et al.Second generation wavelet-based data compression algorithm for power system fault recorder[J].Electric Power Automation Equipment,2004,24(3):59-62.

[10] 闫常友,杨奇逊,刘万顺.基于提升格式的实时数据压缩和重构算法[J].中国电机工程学报,2005,25(9):6-10.

YAN C Y,YANG Q X,LIU W S.A real-time data compression & reconstruction method based on lifting scheme[J].Proceedings of the CSEE,2005,25(9):6-10.

[11] 孙金凤,周国烛,马红麟,等.基于ARM9的整数小波阈值压缩算法及其EVC实现[J].电测与仪表,2007,44(9):45-48.

SUN J F,ZHOU G Z,MA H L,et al.Integer wavelet threshold compression algorithm based on ARM9 and its EVC realization[J].Electrical Measurement & Instrumentation,2007,44(9):45-48.

[12] CALDERBANK A R,DAUBECHIES I,SWELDENS W,et a1.Wavelet transforms that map integers to integers[J].Appl Comput Hormon Anal,1998,5(3):332-369.

[13] 乐全明,郁惟镛,柏传军,等.基于提升算法的电力系统故障录波数据压缩新方案[J].电力系统自动化,2005,29(5):74-78.

LE Q M,YU W Y,BAI C J,et al.Novel compression scheme of fault recording data in power system based on lifting algorithm[J].Automation of Electric Power Systems,2005,29(5):74-78.

[14] SAID A,PEARLMAN W A.An image multiresolution representation for lossless and lossy compression[J].IEEE Transactions on Image Processing,1996,5(9):1303-1310.

[15] 樊建川.电力系统连续录波器数据压缩与存储技术的研究[D].青岛：中国石油大学(华东),2008:38-39.

FAN J C.Research on data compression and storage technology of power system continuous wave recorder[D].Qingdao:China University of Petroleum (East China),2008:38-39.