分时电价体制下原油管道运行优化研究
寇 杰,李春辉,孙 奇,郭勋臣
(1.中国石油大学(华东)储运与建筑工程学院,山东 青岛266580;2.胜利油田石油开发中心有限公司,山东 东营257000)
随着经济的高速发展,对电力的需求在逐步加大。发电厂为了保证用电,在设计发电能力时通常是按照用电高峰时期的容量来设计的。这样,在用电高峰时期就能保证提供足量的电力,但是在用电低谷时期,部分发电设备就会空转闲置。因此,在用电高峰和用电低谷时期的发电成本就产生了差距,所以造成了在不同时段内按照不同的电价进行收费的情况。
输油管道运行优化是降低输油成本的有效措施,一直都是油田集输领域的热点问题。以往国内进行运行优化研究时,通常只考虑如何使泵在高效率区工作,再采用“分时均量”方式输送,即每小时外输量相等,忽略了利用分时电价政策。事实上,峰谷电价相差很大,这就会致使即便外输量一直不变,各时段耗电量相同,一天内不同时段电费也会有很大的差距。以某管道为例,外输泵峰、谷时段耗电情况见表1。

表1 某管道外输泵峰、谷时段耗电情况
由表1可以看出,外输泵在“峰”时段输送了550 m3原油,花费321元,在“谷”时段输送了880 m3原油,却只花费128元,证明目前的“分时均量”输送方式有很大的优化优化空间。
因此,为实现降低电费的目的,可以利用峰谷电价体制,合理调整不同时段管道输量,在完成每天输油任务的前提下,使日电费最少。但是,从管道运行安全角度考虑,受油品本身特性和管道设计压力的限制,不能无限制增加谷时电价期间的输量,同时峰时输量也不能小于最小安全输量。因此,在峰谷电价体制下输量必须控制在一定的范围内[1-5]。本文通过建立原油管道泵送电费数学模型,研究外输油泵优化运行方案,合理安排不同时段输量,达到降低电费的目的。
1 数学模型
本文研究的管道只有一台泵对原油增压,且可通过变频装置调节输量。
将每天分四个时段,设第i时段(i=1、2、3、4,分别对应尖时、峰时、平时、谷时)电价为Ci元/(kW·h),运行ti小时,该时段泵频率为niHz,轴功率为NeikW,该时段管道流量为qim3/h,每天计划输量为Qm3,故每日电费的数学模型,见式(1),约束条件见式(2)~(4)。
(1)
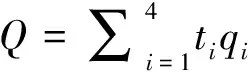
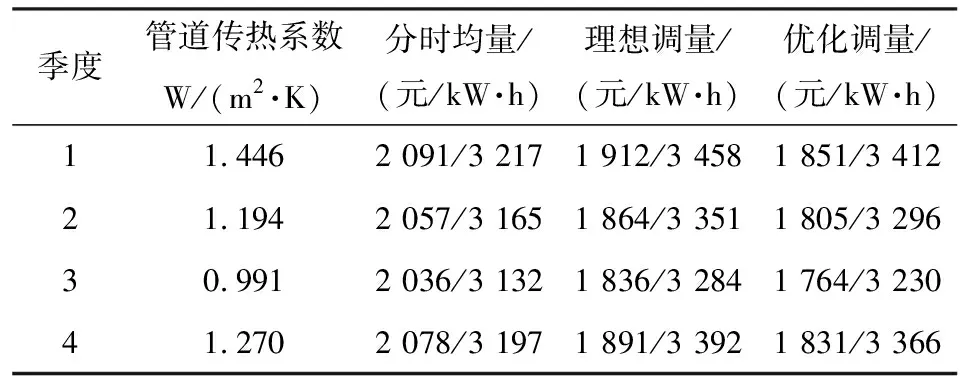
qmin Hc=Hf+Hh(4) 式中:qmin为管道最小安全输量,m3/h;qmax为管道允许最大输量,由管道材质决定,m3/h;Hc为出站压头,m;Hf为管道全线摩阻,由于是长输管道,可近似为沿程摩阻损失,m;Hh为管道起点和终点的高程差,m。 管道最小安全输量需要从热力和管道特性两个方面来确定。使用苏霍夫公式计算管道热力条件允许的最小安全输量;对于管道特性最小安全输量的确定,要计算不同输量时管道的摩阻损失,做出管道的工作特性曲线,找出不稳定工作区,确定管道特性最小安全输量,取二者中较大的作为管道安全输量界限[6-7]。 利用达西公式计算沿程摩阻损失,首先需要确定摩阻系数,摩阻系数与雷诺数有关,而输送过程中油品温度不断降低,雷诺数也随之改变,因此,不能把摩阻系数当做定值。计算时使用Matlab编写程序,把管线分为等距离的若干段,分别计算每一段温降,再求出压降,压降之和即为沿程摩阻损失,称为“分段算法”,这样在保证精度的前提下简化了求解过程。 离心泵输量随频率改变,但同时泵的效率也会变化,Nei由式(5)求解。 (5) 式中:qi为第i时段泵的输量;Hi为第i时段泵在输量qi下泵的扬程;ηi为此时段泵的效率,由相似工况下泵的效率不变原理,若要确定ηi,需先计算输量qi在额定转速n0下对应的相似点q0。 泵额定工况下的特性方程H=A-BQ2-m已知,将通过“分段算法”求出的摩阻Hi和此时的输量qi带入式(6),即可求出此时段泵的转速ni。 (6) 根据离心泵改变转速时输量和转速的关系可以求出相似点q0,进而可以求出此时泵的效率。 沿程摩阻损失与管道输送过程中的温度变化直接相关,因此,求解管道传热系数十分重要。实际运行时,管道传热系数与外界温度有关,考虑到相邻月份外界温度变化不大,把一年分为四个季度,1月、2月、3月为第一季度,以此类推,求解不同季度管道传热系数。为提高管道热力计算的精度,采用“最优化拟合”技术,在特定季度内,最大限度符合所有管道实际温降的K值即为该季度管道的传热系数,为提高求解效率采用LINGO优化软件进行编程求解[8-10]。 遗传算法的基本思想简单,具有全局搜索、简单通用、鲁棒性强等优点[11-13]。各时段输量组合优化问题,可以采用基于整数编码的遗传算法对日电费数学模型进行求解。 1) 步骤一:编码与产生初始种群。使用整数编码,将一条染色体编码成向量ck,染色体长度为4,依次对应尖、峰、平、谷各时段输量,将种群在一定的约束条件下初始化,产生初始可行解,见式(7)。因此,每条初始染色体代表一种可行的输量方案。 (7) 3) 步骤三:遗传操作。对染色体的遗传操作包括选择、交叉、变异。选择操作采用轮盘赌选择法,根据各染色体的适应度,从种群中选出一定规模的个体重组成新种群;交叉操作采用单点交叉方式产生子代,即根据交叉概率挑选两组染色体,把这两组染色体上对应位置的数据互换;变异操作采用均匀多点变异方式产生子代。本文研究的变量之和为定值,所以在交叉前和变异后,需对所得染色体进一步处理以满足要求。 交叉前: 交叉后: 数据处理: 这样处理后,最后得到的数据可满足输量要求。 4) 步骤四:对于子代群体,重复步骤二和步骤三,进行新一轮遗传进化过程,直到迭代收敛(适应度值趋向稳定),可认为找到最优解。 某原油管道全长45.7 km,首站高5.5 m,末站高22 m,管径为Φ 273 mm×15 mm,管壁粗糙度0.1 mm,日输量4 600 m3,首站所在地区“尖时”电价为1.10元/(kW·h),“峰时”电价为1.04元/(kW·h),“平时”电价为0.65元/(kW·h),“谷时”电价为0.26元/(kW·h),各时段分别运行3 h、5 h、8 h,输送一种原油。 表2是各种输量方案结果的对比。优化结果表明,并不是电费最低时输量最大,电费最高时输量最小,这不符合利用分时电价的预期,为了使优化结果更有说服力,引入“理想调量”方案进行对比。“分时均量”输送是油田原来采用的输送方案,即每小时输量相同,“理想调量”输送是指“谷时”以最大输量输送、“尖时”以最小输量输送,“优化调量”输送是优化求得的运行方案。 由表2可以看出,由于各季度管道传热系数的不同,日电费也随之改变。这是因为随着传热系数的增大,油品温降也会变大,导致黏度上升,沿程摩阻损失增加,最终会使泵耗电费变大。因此,三种输量方案都是第三季度日电费最小,第一季度日电费最大。同时,与“分时均量”输送方案相比,两种调量输送方案能节约的日电费也在变小,这是因为调量输送时不同时段输量相差较大,当输量较小时,易受管道传热系数影响,温降较大,沿程摩阻损失增大,最终使电费变大,而“分时均量”输送时输量较大,温降变化不大,电费较为稳定。 表2 各季度输量方案日电费/电量对比 与“分时均量”输送方案相比,后两种输送方案耗电量明显增大,这是由于输量变化较大导致的。一般来说,选泵的时候会考虑尽可能使泵在高效率区工作,当泵输量过小时,泵的效率会降低,需要消耗更多电量;而当输量过大时,由于沿程摩阻损失与输量的平方成正比,摩阻损失会随着输量的增大急剧增大,也会使耗电量显著增加。因此,“分时均量”输送方案耗电量会显著小于后两者,但本文的优化目标是电费最小,可不考虑一定要让泵在高效率区工作。 与“理想调量”方案费用相比,“优化调量”方案费用更少,是最优运行方案。当泵耗电费最小时,“谷时”输量没有达到最大输量,“峰时”输量也不是最小输量,这是由三方面因素造成的:①每天都需要完成额定的输量任务,由于管材承压性能的限制,不能无限制增大输量,管道有一个最大输量,为确保管道安全运行,若是在电价较高的时候都用最小输量输送,在电价较低时即使以最大输量输送也无法完成计划;②优化的目标是日电费最低,需要把四个时段作为一个整体来考虑,各时段所耗电费之和最小才是要求解的目标;③摩阻损失与输量的平方成正比,因此,摩阻损失会随着输量的增大急剧增大,从而使泵耗电费显著增加。从表2也可看出,“理想调量”方案日电费明显大于“优化调量”的日电费。 针对分时电价政策,建立日电费数学模型,并使用遗传算法进行求解。现场验证表明,使用优化方案调量输送可显著降低日电费,这种方法不需要购买新装置,有推广使用的价值。 优化结果表明,要使日电费最低,需要把四个时段作为一个整体来考虑,并不是“谷时”以最大输量、“尖时”以最小输量输送就是最优输送方案。此外,为达到电费最低的目的,不需尽量使泵在高效率区工作。 大气温度的改变会导致管道埋深处自然地温变化,管道传热系数也会随之改变,因此,不同季度的最优输送方案不同。同时,泵耗电费与管道传热系数密切相关,为减小管道传热系数,可在管道上敷设新型保温材料。 精确测定油品性质是优化的前提,随着油田进入开采后期,使用大量药剂辅助开采,油品性质会经常变化,要每隔一段时间重新测定油品性质。 [1] SPARROW D.Implementing Software Systems for Multi-product Pipeline Scheduling[J].Pipes & Pipelines International,1985,30(4):14-18. [2] 赵娟,谭忠富,李强.我国峰谷分时电价的状况分析[J].现代电力,2005,22(2):82-85. [3] VIJERDEN N G.Optimization Pipeline Operation[J].Journal of Petroleum Technology,1980,32(11):2063-2067. [4] 孟振虎,陈毅忠,马平.输油管道运行优化实用分析[J].油气储运,2002,21(4):9-13. [5] 姜海斌,袁运栋,蔡丽君,等.库鄯输油管道最佳经济运行方式的确定[J].油气储运,2002,21(2):40-42. [6] 冯叔初,郭揆常,等.油气集输与矿场加工[M].东营:中国石油大学出版社,2006:149-152. [7] 杨筱衡.输油管道设计与管理[M].东营:中国石油大学出版社,2006:199-201. [8] 张国忠.理地热油管道准周期运行温度研究[J].油气储运,2001,20(6):4-7. [9] 徐铭泽.榆树林油田集输系统骨架管道安全经济运行技术研究[D].大庆:东北石油大学,2015. [10] 刘晓燕,刘扬,孙建刚,等.输油管道运行优化研究[J].工程热物理学报,2004,25(4):558-561. [11] 李海娜,吴家勇,陶江华,等.峰谷电价体制下原油管道输油方案研究研究[J].油气储运,2016,34(4):7-11. [12] 葛继科,邱玉辉,吴春明,等.遗传算法研究综述[J].计算机应用研究,2008,25(10):2911-2916. [13] 曾文飞,张英杰,颜玲.遗传算法的基本原理及其应用研究[J].软件导刊,2009,8(9):54-56.2 模型求解
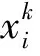
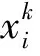
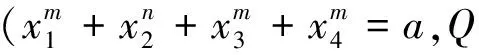
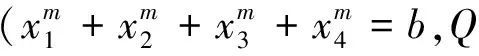
3 案例分析
4 结 论

