基于实物期权的稀土资源投资决策研究

罗宇洁 王静

摘要：本文依据实物期权理论，以动态规划期权定价方法构建了投资决策模型，并以实例对模型进行了运用，对模型参数进行了敏感性分析。研究结果表明，模型比较切合投资的实际情况，计算出的投资项目价值临界值更为科学，为稀土投资决策者提供参考。

关键词：稀土资源；投资决策；实物期权；动态规划

稀土是发展高新科技和国防尖端技术的重要战略资源，对国家经济的发展起到了显著作用。我国稀土资源丰富，资源储量居世界首位，进入21世纪以来，伴随着其他国家及地区稀土矿的相继发现，中国稀土资源在世界稀土资源储量中所占比例进一步降低。稀土资源被过度开采、大范围低价输出，造成稀土资源价值的低估[1]。因此，为了科学开采稀土资源、提高资源利用效率，有必要建立完善的稀土资源投资决策方法。传统的折现现金流法，忽略了管理者根据政策、信息变化修正经营决策的灵活性和实施项目的可延迟性，使得项目投资绝对化，把不确定性以及存在的风险消极化，导致低估稀土资源开采价值，使国有资产流失。

随着实物期权评估方法的日益成熟，有关实物期权在矿产资源价值评估中的应用研究也越来越深人。稀土资源在勘探、开采过程中会受到地质条件、开采工具、管理决策、宏观政策等多方面的影响，具有很大的不确定性和管理的灵活性，具有期权特性，因此，利用实物期权的方法更能全面评估稀土资源的价值。

1 文献回顾 Myers[2]和Ross[3]最早提出了‘实物”期权概念，把投资项目中的管理者拥有的潜在投资机会看作期权。Oscar Miranda等（2013）[4]、杨荣勤等（2015）[5]、王利等（2016）[6]等运用B-S模型、二叉树模型对矿业投资项目、煤炭投资项目不确定性进行了研究，考虑了管理灵活性问题，将拥有的投资机会看做一种期权，不确定性可以增加项目价值，从而对项目价值进行了科学评估o Edgardo Brigatti等（2015）[7]，InthanongsoneInthavongsa等（2016）[8]，王涛、张金锁等（2012）[9]，黄健柏等（2015）[10]，王玲、张金锁、邹绍辉（2016）[11]国内外学者根据Dixit和Pindyck给出的期权定价方法，将矿产资源投资过程看作一个动态优化的过程，通过构建微分方程寻找原函数的方法，求解出煤炭、金属矿、石油勘探等开发投资项目价值和投资机会价值的函数表达式。

通过文献回顾，实物期权相关应用研究模型主要有B-S模型、二叉树模型和动态规划模型。其中动态规划模型主要适用于投资过程优化问题，寻找最优的投资时机，它将投资过程中的不确定性看作积极因素，这些不确定性可以增加投资项目价值。稀土投资过程中有多种不确定性和管理灵活性，稀土价格波动幅度较大，从而投资项目价值的变动较大，何时执行投资决策才能使投资项目价值最大呢？基于以上间题，本文运用动态规划模型对稀土投资决策进行研究。首先分析了稀土资源投资期权特性，然后假设矿产资源价格的变化服从幾何布朗运动，构建动态规划模型，最后求解计算出最大投资项目价值，确定投资最优时机，并对模型进行了实例运用，为稀土资源投资决策提供参考。

2 稀土资源投资的动态规划方法

稀土投资项目具有投资大、不确定性大、投资不可逆和投资可推迟等特点。投资项目的价值受到矿产品价格、成本、市场利率、生产技术等多种不确定性因素的影响，这些不确定性因素引起项目价值的波动，何时投资项目价值最大呢？V表示投资项目价值，F（V）表示投资机会价值（即投资期权价值），通过动态规划法找出使其最大化的投资决策。假设在t时刻，V-I>F（V），表明应该进行投资而不是等待，投资临界点满足V*=F（V*）+I，以该点确定投资时机，一旦V≧V*，投资就是最优的。

假设稀土资源价格均服从几何布朗运动，除价格为随机变量外，其他参数假设为常数。将矿产品价格P定义为服从下面几何布朗运动变化：d P=αPdt+σPdz

式中，α为价格P的瞬时期望报酬率（漂移参数），σ为价格P的瞬时标准差（方差参数），dz为维纳过程增量，隐含着项目的当前价值是已知的，但是未来价值是对数正态分布。

通过动态规划微分方程分别构建期权价值和投资项目价值的微分方程，运用寻找原函数的方法，求得期权价值和投资项目价值的函数表达式。以F（P）表示投资机会价值（即投资期权的价值），V（P）表示投资项目价值，C表示单位生产成本。

最优决策时贝尔曼方程为：

1/2（σP），F”（P）+αPF'（P）-ρF（P）=0 （3）

1/2（σP）2V”（P）+σPV'（P）-ρV（P）+P-C=0 （4）

其中σ为资产价格的漂移参数；r为无风险利率；σ为资产价格波动率。

方程（3）（4）的解可以表示为

F（P）=APβ1 （5）

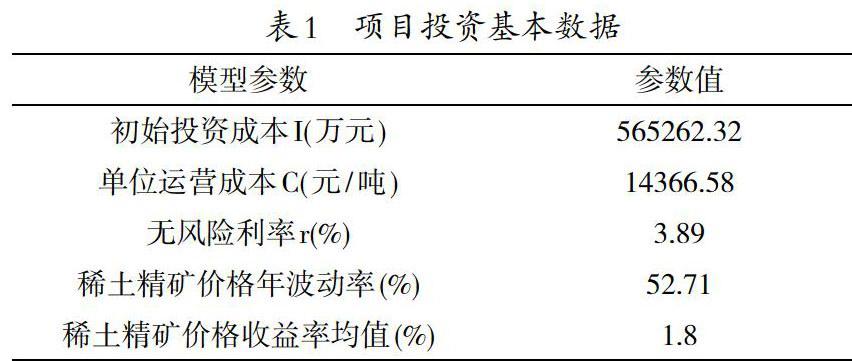
V（P）=KPβ1 P

BPβ2+P/δ-C/r P>C

式中，A、K、B为待定系数，β1和β2由下式求得

通过投资临界处条件求出投资临界值P*，进而求出临界处投资项目价值v伊*）。只有当项目价值V（P）≧V（P*）时，应把握最优的投资时机，立即进行投资，否则，应继续等待。

3 实证研究

3.1 项目基本数据

某稀土企业欲对其所属矿山开采稀土矿产品，为了确定未来最优投资时机，需要对投资决策进行分析。项目中的无风险利率参照同期国债利率；稀土精矿价格收益率均值根据稀土精矿的现货交易均价求得（数据来源于中国金属新闻网、瑞道金属网、中国稀土网）。项目投资基本数据见表1。

采用历史波动率的对数价格法求取资产价格波动率。

对数价格法：

第i天资产的价格；Pi+1是第1+1天资产的价格。

3.3 敏感性分析

以案例中各个参数的取值为基准，令波动率σ、无风险利率r和便利收益δ分别上下变动1%，观察项目临界价值和投资机会价值的变动比率，如表4所示。

由表4可知，稀土价格波动率σ，无风险利率r对项目临界价值V*和投资机会价值F具有正相关性，便利收益具有负相关性。其中，波动率是最敏感参数，而且波动率的增加比减少更能引起项目价值的变动。无风险利率r引起的变动幅度不大，与其相比，便利收益δ引起变动幅度较大，而且便利收益的减少比增加引起的变动幅度大，表明便利收益的减少更能引起项目临界价值的变动，便利收益代表来自存储的边际便利收益，主要反映了资源丰度，资源丰度的降低会引起项目临界价值的提高，相对稀缺的资源具有更高的价值。

4 结论

本文通过构建动态规划实物期权模型，研究了稀土开采投资项目的最优投资时机。本文的主要结论有：①稀土价格波动较大，投资项目中不确定因素较多，投资决策可以看做期权执行问题，同时又是动态规划问题，将两者结合运用动态规划方法求出投资临界值，确定最优投资时机。②稀土价格波动率是项目价值的重要影响因素，通过敏感性分析可知，波动率与项目价值具有正相关性，价格的波动增加了投资项目的价值。便利收益也是项目价值的较为敏感参数，是负相关性，便利收益的减少更能引起项目临界价值的变动。

参考文献：

[1]吴迪，钱贵霞.中国稀土产业经济研究现状与发展趋势分析[J].稀土，2014，35（05）：104-112.

[2]Myers S C， Turnbull S M. Capital budgeting and the capitalasset pricing model：Good news and bad news[J].The Journal ofFinance， 1977，32（2）： 321-333.

[3]Ross S A. A simple approach to the valuation of risky income streams[J].Journal ofBusiness，1978，51： 453-475.

[4]Oscar Miranda，Luiz E. Brandao. A Real Options model to assessan exploration mining project：An application[A].In： 18th AnnualInternational Real Options Conference 2014[C].Colombia，2014：1-20.

[5]基于实物期权的页岩气勘探开发投资决策研究[J].河南科学，2015，33（4）：597-600.

[6]王利.实物期权在煤炭资源开发投资决策中的应用调查研究[J].当代经济，2016 （36）：22-23.

[7]Edgardo Brigatti， Felipe Macias， Max O. Souza， and Jorge P. ZubelliA Hedged Monte Carlo Approach to Real Option Pricing[D].Riode Janeiro， Brazil： IF， UFRJ； DMA， UFF， Brazil. R. M. S. Braga；IMPA，2015.

[8]Inthanongsone Inthavongsa，Carsten Drebenstedt， Jan Bongaerts，Phongpat Sontamino. Real options decision framework： Strategicoperating policies for openpit mine planning[J].Resources Policy，2016，47：142-153.

[9]王濤，张金锁，邹绍辉，金浩.实物期权的煤炭资源勘查投资项目评估模型[J].西安科技大学学报，2012，32（1）：13-18.

[10]黄健柏，谭娜，钟美瑞.基于过度自信的矿产资源开发实物期权决策模型[J].系统工程，2015，33（6）：57-63.

[11]王玲，张金锁，邹绍辉.石油勘探项目分阶段投资的最优时机选[J].数学的实践与认识，2016，46（20）：78-86.