特殊双圈双色有向图的本原指数界

罗美金

(河池学院 数学与统计学院， 广西 宜州 546300)

n阶非负矩阵对(A,B)与其具有n个顶点的伴随有向图D(A,B)存在一一对应关系[1]，即(A,B)中元素的符号和D(A,B)中弧存在与否相对应。例如：设矩阵A=(aij)，B=(bij)，若aij>0(bij>0)，则表示D(A,B)中从顶点i到顶点j存在一条红弧(蓝弧)；相反，不存在红弧(蓝弧)。

只含红弧和蓝弧的有向图D，称为一个双色有向图[2]。若记exp(A,B)为非负本原矩阵对(A,B)的本原指数，exp(D(A,B))为非负本原矩阵对(A,B)所对应的伴随有向图(即双色有向图)D(A,B)的本原指数，根据两者的对应关系，则有exp(A,B)=exp(D(A,B))。因此，类似非负矩阵对本原指数的概念，可定义双色有向图的本原指数的概念为：

若存在非负整数h和k，且h+k>0，使得D中的每一对顶点(i,j)都存在从i到j的(h,k)-途径，则双色有向图D是本原的，且h+k的最小值为双色有向图D的本原指数，记作exp(D)，其中h和k分别表示一条途径中红弧和蓝弧的条数[2]。

设C={γ1,γ2,…,γl}是D的圈集合，D的圈矩阵为M，若M的秩小于2，则M的content(记为content(M))定义为0，否则定义content(M)为M的所有非零2阶主子式的最大公因数[2]。

引理1[1]一个至少包含一条红弧和一条蓝弧的双色有向图D是本原的，当且仅当D是强连通的，且content(M)=1。

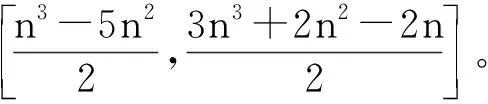
根据非负矩阵对与双色有向图的对应关系，通过双色有向图本原指数的研究能得出相应非负矩阵对的本原指数。近几年，国内外专家、学者关于非负矩阵对本原指数的研究主要集中在特殊双色有向图指数问题的研究，已经取得了一些重要成果[1-8]；在双色有向图本原指数界的基础上，可以进一步推广研究，如含有两个圈的双色有向图本原指数集[9-10]和含有三个圈的三色有向图本原指数上界[11-13]。本文研究了如图1所示的一类特殊双色有向图D，通过非负矩阵对与其伴随有向图的对应关系，在文献研究方法的基础上，借助非负矩阵对的逆矩阵找到了任意顶点对(i,j)都存在从i到j的(h,k)-途径，给出了双色有向图D的本原条件，找到了指数上下界，并对达到指数上下界时的极图进行了刻化。所得结果为非负矩阵对本原指数集、非负矩阵簇指数问题的研究奠定基础。

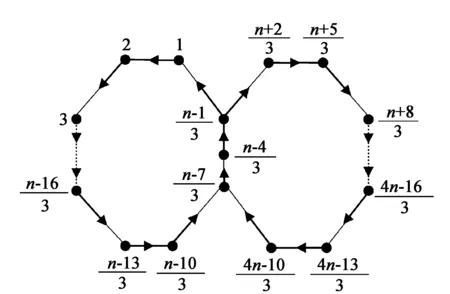
图1 未着色有向图D

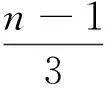
(1)

其中x,y都是整数。

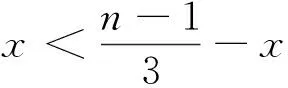
1 本原条件

定理1 如图1所示的双色有向图D是本原的，当且仅当x=1，y=3。

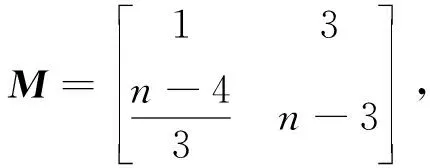
2 指数下界

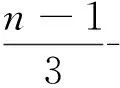
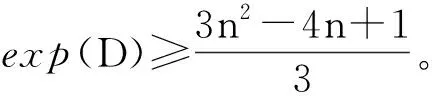
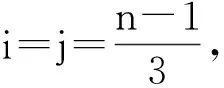
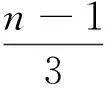
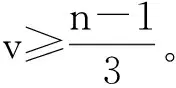
则u≥2n-1。从而

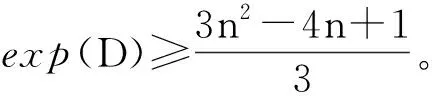
3 指数上界

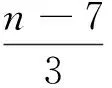
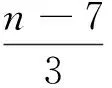
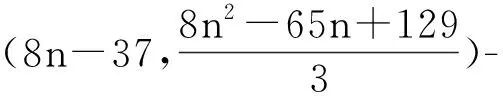
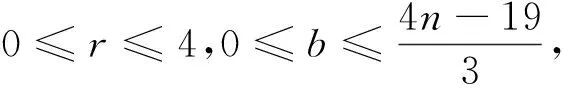
定理得证。

类似定理3的证明过程，可得定理4，不再赘述。

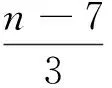
4 极图刻化

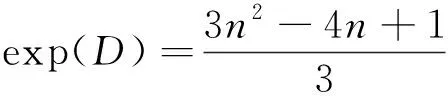
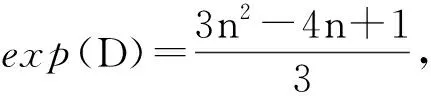
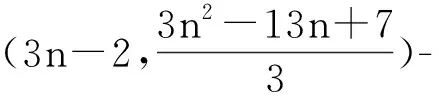
(2)

考虑以下5种情形：

情形1：r=0时。

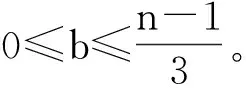
情形2：r=1时。

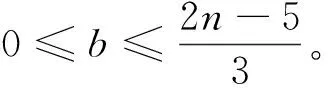
情形3：r=2时。

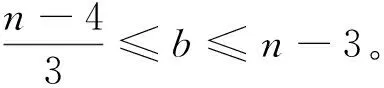
情形4：r=3时。

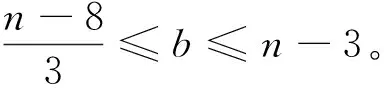
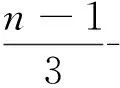
情形5：r=4时。

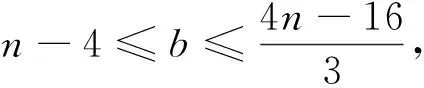
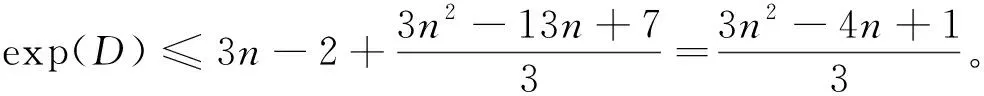
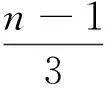
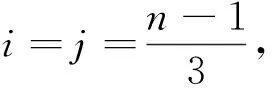
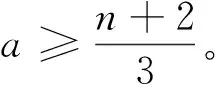
则u≥3a。从而

综上所述，结合定理2，定理得证。

类似定理2和定理5的证明过程，可得定理6和定理7，不再赘述。

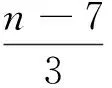
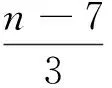
[ 参 考 文 献 ]

[1] SHADER B L,SUWILO S.Exponents of nonnegative matrix pairs[J].Linear Algebra and its Applications,2003,363:275-293.

[2] FORNASINI E,VALCHER M E.Primitivity of positive matrix pairs:algebraic characterization graph theoretic description,and 2D systems interpretation,SIAM[J].Siam Journal on Matrix Analysis & Applications,1998,19(1):71-88.

[3] WIELANDT H.Unzerlegbare,nicht negative Matrizen.Mathematische Zeitschrift,1950,52(1):642-648.

[4] DULMAGE A L,MENDELSOHN N S.Coverings of bipartite graphs.Canadian Journal of Mathematics,1958(10):517-534.

[5] 汪荣,邵燕灵,高玉斌.一类双色有向图本原指数的上界[J].吉林大学学报(理学版),2008,46(4):601-606.

[6] 孙涛,王建中,罗美金.一类双色有向图的指数上界[J].中北大学学报(自然科学版),2011,32(6):655-661.

[7] SUMARD H,SUWILO S.The scrambling index of two-colored two cycles whose lengths differ by 1[J].Far East Journal of Mathematical Science,2015,96(1):113-132.

[8] 李茜,罗美金.特殊双色有向图的本原指数[J].曲阜师范大学学报,2015,41(4):48-50.

[9] 李茜,罗美金.特殊双色有向图的本原指数的上界[J].贵州师范大学学报(自然科学版),2017,35(2):58-61.

[10] 罗美金.一类恰含一个公共点的双色有向图的本原指数集[J].暨南大学学报(自然科学版),2013,34(5):483-488.

[11] 罗美金,侯宗毅.一类特殊非负矩阵对本原指数集[J].重庆师范大学学报(自然科学版),2017,34(2):59-66.

[12] 罗美金,侯宗毅,李茜.一类恰含一个3-圈的三色本原有向图指数上界[J].数学实践与认识,2017,47(20):140-146.

[13] LUO Mei-jin,LI Xi.Exponents of a class of primitive three-colored digraphs[J].Ars Combinatoria,2017,133:179-195.