孔隙水对河堤加筋挡墙静力学特性影响的物理模型试验分析

李泊溪，赵 磊

(辽宁天阳工程技术咨询服务有限公司，辽宁 沈阳 110001)

当前，孔隙水对河道堤防生态加筋挡墙稳定性影响较大，为设计河道堤防生态加筋的稳定性，需要分析孔隙水对河道堤防生态加筋的静力学特性进行研究，近些年来，国内许多学者结合土力学模型分析孔隙水对河道堤防的稳定性影响[1- 6]，这些成果均认为孔隙水与河道堤防之间土层压力存在较大的相关性，对河道堤防的稳定性影响较大。近些年来，生态加筋挡墙在河道堤防工程设计中逐步得到应用[7- 9]，而孔隙水对河道生态加筋挡墙的静力学特性影响研究较少，为此本文引入静力学模型并结合物理模型试验方式分析孔隙水对河道堤防生态加筋挡墙的静力学特性的影响。研究成果将为分析孔隙水对河道生态加筋挡墙稳定影响提供参考依据。

1 计算模型原理

孔隙水对生态加筋挡墙静力学特性的影响，其主要生态加筋挡墙的土压力的计算，其土压力系数进行计算，计算方程为：

(1)

式中，Ka—土压力系数；θ—生态加筋挡墙的水平方向夹角，(°)；φ—土层内摩擦角，(°)。

当第i层生态加筋挡墙栅格垂向距离在6m以下，土层压力系数计算方程为：

(2)

式中，Ki—第i层土层压力系数值；Kj’—土层静力学压力系数；Zi—第i根加筋栅格的垂向距离，m。

当第i层生态加筋挡墙栅格垂向距离在6m以上时，土层压力系数计算方程为：

(3)

在土层静力学计算的基础上，生态加筋挡墙面板的垂向压力计算方程：

σzi=Kiγzi

(4)

在进行垂向压力的同时，对生态加筋挡墙水平方向的压力进行计算，计算方程为：

(5)

式中，q—单位栅格加载的强度，kPa；Lc—生态加筋挡墙荷载宽度，m；Lci—垂向距离zi的扩散性荷载强度，kPa。

则作用在生态加筋挡墙水平方向上的总压力计算方程为：

∑σEi=σzi+σai

(6)

式中，σEi—水平方向上的总压力，kPa。

垂向距离zi处各栅格水平方向拉力计算方程为：

Ti=∑σEi·Sy

(7)

式中，Ti—水平方向上总的压力，kPa。

则垂向距离上的加筋挡墙的抗拔强度计算方程为：

(8)

式中，Tpi—垂向距离的抗拔强度值，kPa；f′—土层之间的摩擦系数值；bi—加筋挡墙的栅格宽度，m；Lai—生态加筋挡墙的锚固长度，m。

理论计算模型采用以下方程对孔隙水影响下的生态加筋挡墙的静力稳定性进行验证，验证方程为：

Tpi>γ0γR1γQ1Ti

(9)

式中，γ0—强度系数；γR1—栅格加筋挡墙的强度调节系数；γQ1—荷载压力系数。

孔隙水对生态加筋挡墙抗拉强度验算方程为：

TK>γ0γR1γfγR2Ti

(10)

式中，γR2—栅格加筋挡墙的抗拉调节系数；γf—栅格分项调节系数。

2 模型应用

2.1 物理试验说明

为分析孔隙水河道堤防生态加筋挡墙的静力学特性的影响，分别结合稳定性试验和充水破坏试验分析孔隙水对河道堤防生态加筋挡墙的稳定

性和抗拔强度。其中在稳定性试验中，分别计算了不同垂向深度下的稳定系数。在充水试验中，分析不同充水条件下孔隙水对河堤加筋挡墙的破坏程度，并结合透水试验分析不同直径钢筋下挡墙的透水率。

2.2 孔隙水对生态加筋挡墙静力影响下的稳定性试验

为分析孔隙水对河道堤防生态加筋挡墙静力影响下的稳定性，对不同垂向深度下的孔隙水对生态加筋挡墙的稳定系数进行了计算，分析计算结果见表1。

从表1中可以看出，随着生态加筋挡墙垂向距离的增加，其稳定系数在0.55～0.79之间变化，总体处于稳定状态。当垂向距在1.95m后，其稳定系数变幅较小，生态加筋挡墙的面板压力也逐步趋于稳定，这主要是因为随着垂向深度的增加，孔隙水对河道堤防生态加筋挡墙的影响也逐步减弱，其河道堤防生态加筋挡墙的稳定性系数变化幅度减小，逐步趋于稳定。因此垂向深度为2.00m时，其达到最佳的稳定状态。

2.3 充水试验下生态加筋挡墙的强度破坏试验

在稳定性分析的基础上，结合充水试验分析了不同充水条件下孔隙水对河道生态加筋挡墙的破坏强度吗，试验分析结果见表2。

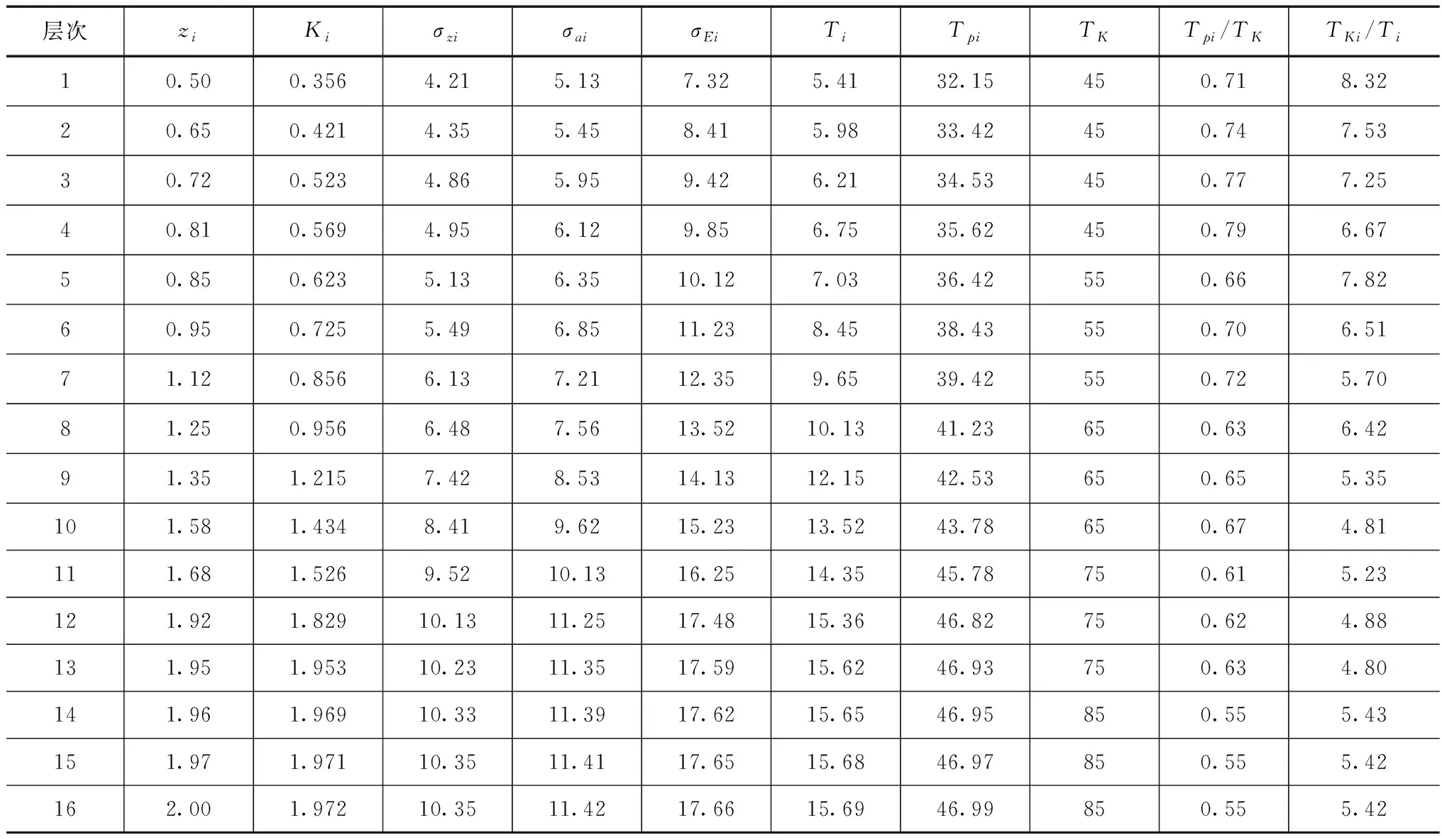
表1 孔隙水对生态加加筋挡墙静力影响下的稳定性试验

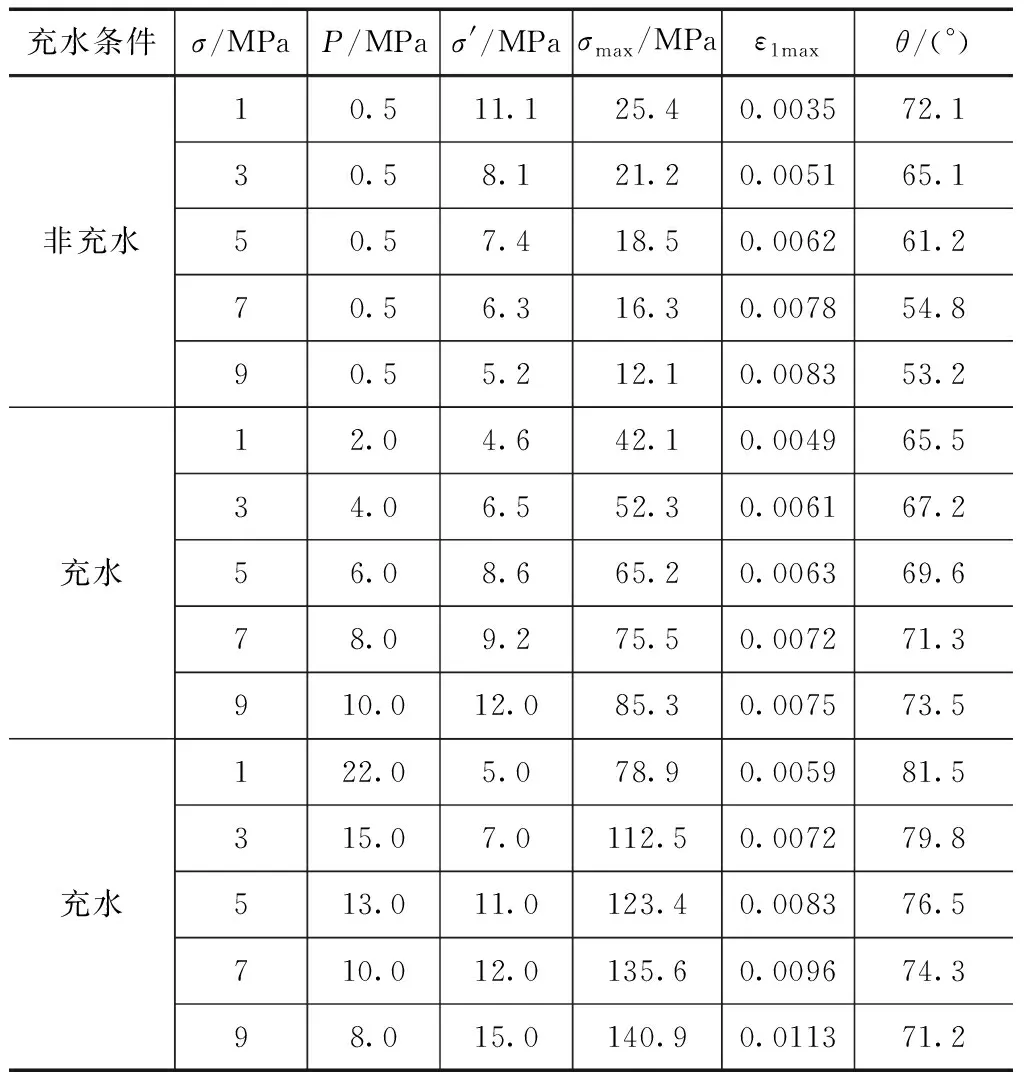
表2孔隙充水试验下对生态加加筋挡墙强度破坏试验结果

充水条件σ/MPaP/MPaσ'/MPaσmax/MPaε1maxθ/(°)非充水10.511.125.40.003572.130.58.121.20.005165.150.57.418.50.006261.270.56.316.30.007854.890.55.212.10.008353.2充水12.04.642.10.004965.534.06.552.30.006167.256.08.665.20.006369.678.09.275.50.007271.3910.012.085.30.007573.5充水122.05.078.90.005981.5315.07.0112.50.007279.8513.011.0123.40.008376.5710.012.0135.60.009674.398.015.0140.90.011371.2

从表2中可以看出，河道堤防生态加筋挡墙在同一压力条件下，相比于非充水条件，其孔隙水对河道堤防生态加筋挡墙破坏程度最为明显，其中随着孔隙水压力的逐渐增大，河道堤防加筋挡墙在水平和垂直方向的峰值破坏度均呈现增加的变化趋势，其中在充水条件下，其峰值破坏度σmax在42.1～140.9MPa之间变化，非充水条件生态加筋挡墙的压力逐渐减小且峰值破坏强度有所减弱。

2.4 正向透水下生态加筋挡墙的透水试验

在破坏强度试验的基础上，结合正向透水试验分析了不同钢筋直径下的挡墙的透水率，试验分析结果见表3和图1。

表3 不同生态加筋直径下挡墙的正向透水试验结果

注：φ表示加筋直径;各水头下数值表示透水率，mm/L。

图1 不同直径下生态加筋挡墙的透水率变化过程

从表3中可以看出，随着孔隙水水头的增加，各直径下的生态加筋挡墙的透水率逐步增加，这主要是因为在正向透水试验下，随着孔隙水头的增加，河道堤防生态加筋挡墙的水平和垂向的压力逐步增加，使得各直径下的生态加筋挡墙的透水率增加。从表中还可看出，随着直径的增加同一孔隙水水头下，其透水率也逐步增加，这主要是因为直径增加后，其透水量也逐步增加，使得透水率逐步加大。从图1中可以看出，在φ从10mm增加大20mm时，其不同水头的透水率变化呈现曲线变化，而从25mm开始起透水率变化较为单一稳定。这主要是因为在较小直径下，河道堤防生态加筋挡墙的透水率受到影响要素较多，而较大直径后，这种影响逐步削弱，使得其透水率变化较为稳定。

2.5 充水条件下孔隙水对生态加筋挡墙的有效峰值破坏强度试验

为分析孔隙水对河道堤防生态加筋挡墙有效峰值的破坏强度，结合充水试验分析了不同强度下的挡墙有效峰值的破坏强度，并分析了不同充水条件下河道堤防生态加筋挡墙的τ～σ关系曲线，结果见表4、5及图2。

表4 非充水条件下的生态加筋挡墙有效峰值破坏强度试验结果

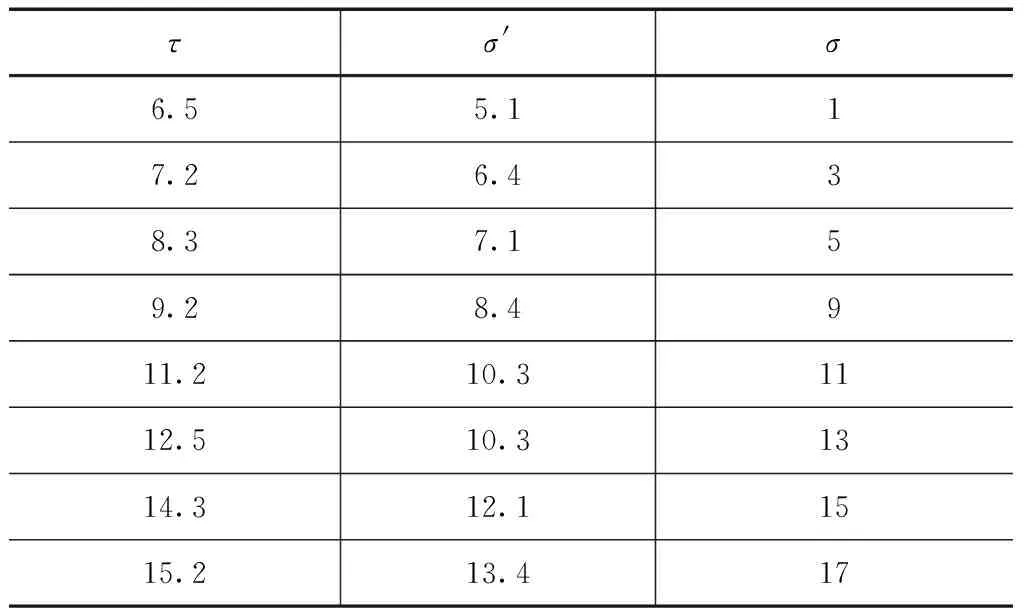
表5 水条件下的生态加筋挡墙有效峰值破坏强度试验结果

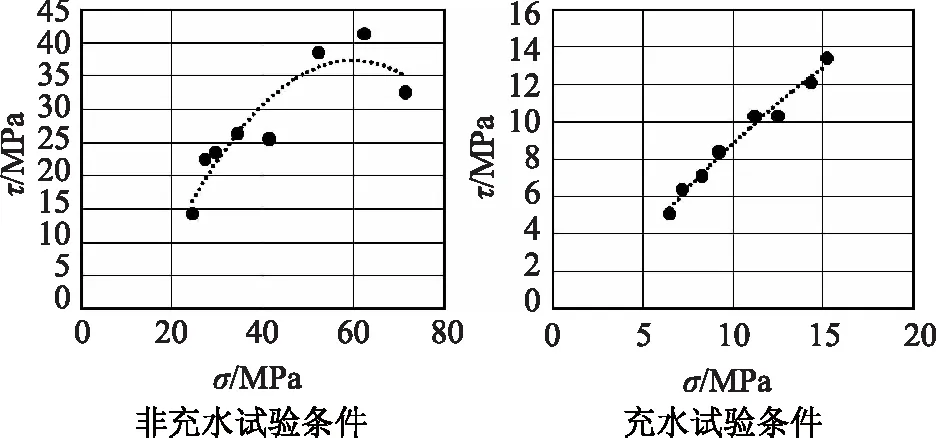
图2 充水试验条件下生态加筋挡墙τ～σ关系曲线

从表4、5中可以看出，在非充水条件下，由于孔隙水的左右，其河道堤防的生态加筋挡墙受到水压力的作用，其有效峰值破坏强度逐步增加，随着孔隙水有效破坏度的增加，随和孔隙水有效压力的增加，其对生态加筋挡墙的破坏程度逐步增加，但幅度逐步减弱。而在充水条件下，随着孔隙水有效压力的增加，其对对生态加筋挡墙的破坏程度逐步增加，但幅度增加较为明显。从图2中可以看出，充水条件下生态加筋挡墙的τ～σ关系曲线呈现明显线性变化，而非充水条件下则呈现较为复杂的曲线变化。

3 结语

本文结合物理模型观测试验方式分析孔隙水对河道堤防生态加筋挡墙的静力学特性影响，试验取得以下结论：

(1)垂向深度的增加，孔隙水对河道堤防生态加筋挡墙的影响较大，其稳定性逐步减弱但趋于稳定，在实际工程中，应首先确定孔隙水对河道堤防生态加筋挡墙影响的最佳垂向深度。

(2)充水条件下，随着水头增加，孔隙水对河道堤防生态加筋挡墙的强度破坏逐步增加，应尽量减少孔隙水压力。

(3)直径大小直接影响孔隙水对堤防生态加筋挡墙静水压力，在工程设计中，应合理设置直径大小，减少孔隙水的静水压力。

[1] 赵巍巍. 小凌河羊山段河道堤防及护坡稳定分析[J]. 黑龙江水利, 2017(01): 83- 87.

[2] 赵正玲. 河道新型加筋土挡墙护岸结构设计分析[J]. 水利技术监督, 2012(05): 49- 51.

[3] 张智酝, 张绍广, 陶娟, 等. 基于AutoBank的淮安市黄河故道地区上段河道堤防渗流稳定分析[J]. 治淮, 2014(09): 25- 26.

[4] 彭超, 徐洲平. 生态袋挡墙护坡技术在运河航道整治工程中的应用[J]. 水利规划与设计, 2010(05): 100- 102.

[5] 张娟. 大同市口泉河河道治理堤防稳定设计[J]. 山西水利, 2010(04): 36- 37.

[6] 岳景哲. 新型加筋土挡墙结构设计与探索[J]. 水利规划与设计, 2010(05): 72- 75.

[7] 王博军. 生态袋加筋挡墙工作机理研究[D]. 河北工业大学, 2014.

[8] 杨政文, 李涛, 祝勇军. 生态袋护坡加筋挡墙结构研究[J]. 山西建筑, 201(19): 126- 128.

[9] 申超. 高速公路柔性生态加筋土挡墙现场监测与设计方法研究[D]. 中南大学, 2012.