基于模态参与因子的白车身动刚度优化
江想莲、耿福荣、戴太亮
(广汽研究院 510000)
0 引言
随着消费者对汽车的要求越来越高,汽车的NVH性能也成消费者非常关注的性能指标之一。车辆在怠速或行驶过程中,由车身面板振动引起的室内空腔轰鸣噪声对乘坐舒适性有很大影响。其中,通过发动机、悬架等接附点传递至车身的振动是引起车身面板振动的主要原因[1]。同时,接附点的动刚度强弱对车身的疲劳寿命有很大的影响,当外在激励与车身的某阶模态的固有频率接近时,将可能导致结构共振,致使结构易疲劳破坏。高的接附点动刚度不仅提升了安装点与其隔振衬套的刚度比,同时增加了安装点对发动机、路面激励的隔振作用。因此,车身接附点的动刚度对车身振动和噪声、疲劳有着较大的影响,是在整车NVH分析中需要首先考虑的因素之一[2]。
在车型开发项目中,传统接附点的动刚度优化主要依靠经验对零件的厚度和结构进行优化设计,需要进行大量的仿真验算工作从而达到设计目标,优化时间周期较长。本文则采用模态参与因子分析法,快速高效对后减振器接附点的动刚度进行优化,使其满足性能要求,并节省大量的设计周期。
1 车身动刚度分析理论
动刚度是结构在特定的动态激扰下抵抗变形的能力,动刚度分析主要通过频率响应分析,计算结构在周期振荡载荷作用下对频率的动响应。激励载荷的形式可以是外力或强迫运动(位移、速度和加速度等),计算结果分实部和虚部两部分,实部代表响应的幅度,虚部代表响应的相角。动刚度采用响应的幅值来表示,包括节点位移、加速度、单元力和应力等。
动刚度的计算方法主要有直接频率响应和模态频率响应2种。其中,直接频率响应是通过求解整个模型的阻尼耦合方程,得出各频率对于外载荷的响应。
模态频率响应则是利用结构的模态振型,来对耦合的运动方程进行缩减和解耦,同时由单个模态响应的叠加得到某一给定频率下的解答。其分析的输出类型与直接频率响应分析得到的输出类型相同[3]。模态频率响应分析法利用结构的模态振型来对运动方程进行缩减,因此在对较大模型做频率响应分析时,比直接频率法更有效率。
在本车型的频率响应计算中使用模态频率响应,下面是模态频率响应理论的简介[4]。
多自由度系统的模态方程一般可写为:

式(1)中:F为激励向量;X为响应向量;M为质量矩阵;C为阻尼矩阵;K为刚度矩阵。
通过对式(1)进行拉氏变换和模态解耦得到以下关系方程[5]:
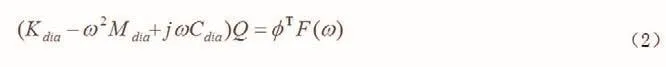
式(2)中:Kdia、Mdia和Cdia分别为主刚度矩阵、主质量矩阵和主阻尼矩阵。
对式(2)进行展开,可以求得第r阶模态对应的解为:

把模态坐标转换为物理坐标,可以得到物理坐标测点L的响应为:
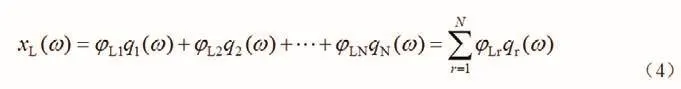
假设对单点p进行激励力为F,对单点L点进行响应分析。其中激励力F的表达式为:
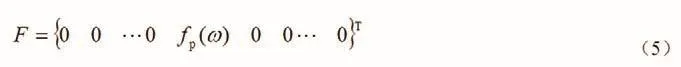
通过式(3)得到对应激励点p的第r阶模态的对应解为:

通过式(4)中得到:

通过(7)式,从而可以得到响应点L与输入点P之间的频响函数为:

当响应点L与输入点P为同一点时,式(8)就变为原点的频响函数(也即为原点动刚度的倒数):

基于模态频率响应的理论,响应点的动刚度(位移幅值)即为各阶模态(激起的相位)对该点的位移叠加和耦合。模态对该点位移的贡献量即为模态参与因子。通过频率响应分析,可以找出某些频率出现的峰值。模态参与因子分析则可找出峰值频率处的响应是由哪些主要的模态的响应叠加而成的,并按要求输出模态贡献量较大的几个模态,根据模态的振型进行优化设计。模态参与因子分析法能高效地辅助动刚度的优化设计,并可广泛运用于整车NVH分析优化。
2 某车型动态刚度分析与优化方案
减振器接附点动刚度的大小,对衰减来自路面的振动具有重要的意义。本文通过对后减振器接附点动刚度进行分析,提出了优化方案,使得后悬置接附点动刚度满足了NVH目标要求。
在某车型项目中,对后塔座周围的结构件进行轻量化优化,并且保证后减振器接附点的动刚度满足目标曲线。如图1和图2所示为轻量化前后的后减振器安装点周围结构图,主要结构变化包括V型梁由钣金变为管梁结构,以及减振塔座结构优化。现对结构轻量化前后的减振器接附点进行频率响应分析,分别输出X、Y、Z三个方向频率与加速度曲线,如图3所示,实线为基础目标曲线(轻量化前),虚线为设计方案1的结果曲线(轻量化后)。
根据图3中的曲线显示,X方向的动刚度与基础目标曲线相当,Y方向116 Hz的峰值点刚度低于基础目标曲线,Z方向上120 Hz峰值点的刚度低于基础目标曲线。在该设计变化前后,这2个峰值点均不满足目标要求,需要进行结构优化。现采用模态参与因子搜寻贡献度较大的模态,对其振型进行判断,进一步进行结构优化。从上述分析结果,拟对116 Hz的Y向、120 Hz的Z向模态参与因子进行输出。如表1和表2所示,模态贡献较高前5位的阶次排序于列表中。

图1 轻量化前的后减振器安装点周围结构图

图2 轻量化后的后减振器安装点周围结构图

图3 后减振器接附点的频率与X、Y、Z向加速度曲线图

表1 模态对后减振器接附点116 Hz的Y向响应参与因子列表

表2 模态对后减振器接附点120 Hz的Z向响应参与因子列表
分别将上述116 Hz的Y向、120 Hz的Z向模态参与因子排序前3位的模态振型幅值进行分析,如图4和图5所示。从模态的幅值云图不难看出,116 Hz的Y向刚度主要受横梁的Y向刚度以及管梁的Y向刚度影响,若要提高116 Hz的Y向刚度,即要提高横梁的Y向刚度和管梁结构的稳定性和刚度。而120 Hz的Z向刚度主要受塔座的连接刚度及管梁的Z向刚度影响,需通过加强塔座的连接刚度及管梁的Z向刚度。
根据上述模态振型幅值图的分析结果,针对管梁和塔座Y、Z向的刚度不足,对现有结构进一步优化。如图6所示,两个管梁断头进行焊接汇合,并与连接板进行焊接;同时管径由原来的20 mm增加到30 mm;塔座横梁与轮罩的连接板结构优化,并增加连接焊点;塔座板增加加强筋,并优化其与侧围的连接焊点[6]。
对上述优化结构后的减振器接附点进行频率响应分析,输出X、Y、Z三个方向频率与加速度曲线,如图7所示,实线为基础目标曲线(轻量化前),虚线为设计方案1结果曲线(优化后)。结果显示,116 Hz的Y向、120 Hz的Z向峰值较轻量化前的结果明显降低,并且在50~250 Hz整个区域的动刚度略优于轻量化前的刚度,满足动刚度的优化要求。

图4 117.04 Hz、121.38 Hz、117.42 Hz模态振型Y向幅值云图

图5 121.38 Hz、122.97 Hz 、119.72 Hz模态振型Z向幅值云图
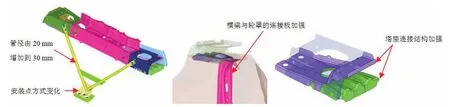
图6 后减振器接附点的结构优化图
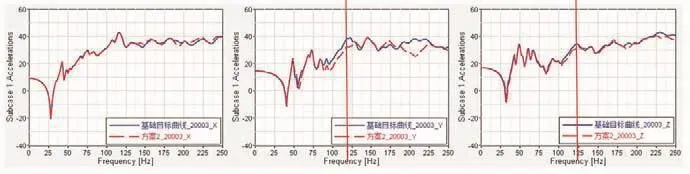
图7 优化后减振器接附点的频率与X、Y、Z向加速度曲线图
3 结束语
(1)采用模态参与因子法对后减振器接附点动刚度进行优化,使其满足与轻量化前的动刚度要求。
(2)模态参与因子法的应用,提高动刚度的优化效率,可广泛应用于NVH性能优化分析。
(3)本文仅通过仿真手段横向对比优化,其优化结构尚未进行动刚度的试验验证,有待下一步制作样件进行实车验证。
[1]Cogswell James A.Mechanical Mobility Relationship to theDynamic Properties of the Structure-Borne Vibration Pathwithin the Power Train and Vehicle.SAE Paper,2003-01-1601.
[2]Kim K,Choi I.Design Optimization Analysis of Body Attachment for NVH Performance Improvements[J].SAE Paper,2003-01-1604.
[3]庞剑,谌刚.汽车噪声与振动[M].北京:北京理工大学出版社,2006.
[4]邹途祥,张军.车身接附点动刚度的研究.LMS,2013.
[5]倪振华.振动力学[M].西安:西安交通大学出版社,1988.
[6]傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000.

