储气库注采管柱静、动力学安全性评价及软件开发

丁建东 练章华 丁熠然 张强 李华彦 刘靓雯

1.华北油田公司工程技术研究院；2. 西南石油大学油气藏地质及开发工程国家重点实验室

地下储气库［1］是将长输管道输送来的天然气重新注入地下封闭空间而形成的一种人工气田或气藏。由于储气库在天然气生产调峰和资源储备方面具有不可替代的作用，近年来在国内外迎来了快速发展［2-7］。在储气库运行过程中，储气井每年循环一个注采周期，地层压力和井筒温度发生周期性的变化，注采管柱将承受温度变化及拉压交变载荷，这将在一定程度上影响管柱的力学强度安全性［8］。因此，对注采工况下油管柱的安全性进行评价具有极为重要的意义。1962年Lubinski等［9］建立了井下封隔器-管柱力学模型，研究了鼓胀效应、活塞效应、温度效应以及螺旋弯曲效应引起的油管柱长度变化。随后，Hammerlindl［10-12］以及 Mitchell［13-14］在 Lubinski螺旋弯曲理论的基础上，进一步讨论了带封隔器多级管柱的受力问题以及管柱中和点的计算问题，为井下带封隔器管柱的安全性评价奠定了力学基础。在国内，黄桢［15］、李子丰［16］和练章华［17-20］等在前人研究的基础上，开展了不同工况下油管柱的静、动力学强度分析及安全性评价。但以前的研究重点主要在压裂、酸化的液体介质工况下的管柱力学问题，对于储气库高速交变注采特殊工况下管柱的静、动力学强度及安全性评价方面的文献不多。

针对储气库注气和采气工况，开展了注采管柱静、动力学强度安全性评价研究，在前人研究的管柱力学研究成果以及本文建立的管柱力学计算模型的基础上，开发了具有自主知识产权的储气库注采管柱静、动力学安全性评价软件，应用该软件对现场储气井进行了安全性评价的应用分析，为储气井注采参数的优化或优选以及注采管柱安全的运行提供了理论依据和指导。

1 封隔器对油管的作用力

封隔器与油管柱的关系分为不可移动、有限移动和不可移动3类，不可移动封隔器-油管柱是本文主要研究的主要内容。封隔器坐封后井下温度压力的变化会引起油管柱纵向长度与受力的变化，封隔器会对油管柱产生一个作用力，而该作用力Fp对油管柱最终实际受力和屈曲状态起着至关重要的作用［21］，同时如果封隔器对油管柱的作用过大还可能造成封隔器损坏，许多文献都未对此进行深入的分析以及求解。

由于封隔器对油管柱存在位移约束，当油管柱的内外温度和压力发生变化时，封隔器必定对油管柱产生一个作用力以阻止油管柱移动。要求封隔器对油管的作用力Fp，先假设油管柱下端未受封隔器约束，计算出各种效应下油管柱的总变形量∆Lp，然后施加一个能使油管柱恢复到它未发生变形位置的作用力，即在油管柱下端施加的Fp。如果该力Fp是对油管柱的压缩力，则计算虎克定律和螺旋屈曲的变化长度；如果是拉伸力，则只含虎克定律的长度变化，其变形计算如下：

根据上式，求出Fp的计算式为

对于不能移动的封隔器而言，最终作用在油管上的实际力Fa*和产生螺旋弯曲的最终虚构力Ff*分别为

式中，Fp为封隔器对油管的作用力，N；∆Lp为油管柱在温度压力效应下的总变形量，m；L为油管柱总长度，m；E为油管弹性模量，Pa；I为油管的截面惯性矩，m4；As为油管横截面积，m2；r为油套管间的径向间隙，m；W为单位长度的油管重量，kg/m；Fa*为最终作用在油管上的实际力，N；Ff*为产生螺旋弯曲的最终虚构力，N；Ap为封隔器密封腔的横截面积，m2；Ai为油管内截面积，m2；Ao为油管外截面积，Pa；pi为封隔器处油管内部的压力，Pa；po为封隔器处环形空间的压力，Pa。

2 管柱动力学分析

2.1 有限元模型建立

油管柱属于细长管柱，油管柱振动的动力学问题是一个相当复杂的过程。根据储气库注采管柱的实际结构和受力特点，本文建立了油管柱振动的有限元模型（见图1），其中，油管外径为88.9 mm，壁厚为6.45 mm，油管柱长度为4244 m。选择PIPE288单元类型，能够模拟管柱在承受内外流体压力作用下的振动情况。从静力学上分析，油管柱承受的静力载荷主要包括：在井口B点处井口拉力Ft，油管柱在其底部封隔器A点处受封隔器的力Fp以及管柱在内外流体中的重力Fg。而油管柱承受的动力载荷主要是高产气井中高速气流诱发引起的冲击载荷，因此油管柱的振动主要是由高速气流对油管内壁的摩阻力引起的。

图1 油管柱有限元模型Fig. 1 Finite element model of tubing string

提取中和点以下4个关键点（图1中H1、H2、H3和H4）的数据进行分析，其与封隔器的距离分别为10 m、50 m、150 m和250 m。由于管柱受拉伸不会产生屈曲损伤，只有中和点以下管柱受压缩的振动才会产生屈曲损伤问题，因此，本文重点分析中和点以下油管柱的振动问题。

2.2 固有频率及振型分析

利用有限元分析软件ANSYS对油管柱进行模态分析，计算得到管柱的前10阶振动频率，如表1所示，管柱第1阶振动频率为0.0165 Hz，且管柱振动频率随振动阶数的增加而逐渐增加，管柱第10阶振动频率达到0.1672 Hz。

表1 油管柱前10阶振动频率Table 1 Vibration frequencу of tubing string in thefirst 10 stages

当储气井气量改变时，管柱振动频率与气量之间的关系曲线如图2所示。随着气量的增加，管柱前5阶振动频率均呈下降的趋势。当气量增加至30万m3/d时，管柱振动频率的下降趋势变陡，且当气量超过35万m3/d时，管柱第1阶振动频率已为0，说明在不同的气量下，管柱将会产生不同形式的振动，因此能够通过优化注采气量来改善油管柱的振动问题。

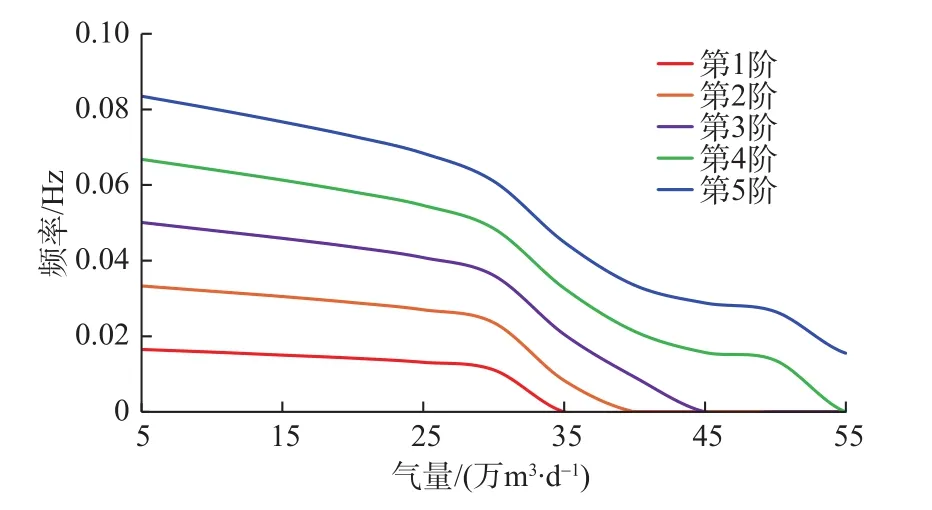
图2 管柱振动频率与气量关系曲线Fig. 2 Relationship of string vibration frequencу vs. gas production

管柱的各阶振型见图3，可以看出，各阶振型沿井深的分布并不是完全对称的，从井口到封隔器，其振型形状由稀到密，振型最大位移由小到大，即振型的最大位移发生在油管柱下端封隔器上部区域，因此包括井口管柱在内（井口轴向力最大），封隔器处也是管柱力学强度评价的关键部位。

2.3 瞬态动力学研究

图3 管柱各阶振型Fig. 3 Vibration tуpe of string in each stage

在模态分析的基础上，根据华北油田苏桥储气库的实际生产工况，对管柱施加采气产量为67万m3/d的冲击动力载荷，进行瞬态动力学研究，得到距封隔器10 m、50 m、150 m和250 m处管柱的纵向振动位移、速度和加速度随时间的变化关系（见图4～图6），可以看出，距封隔器10 m处管柱的振幅最小，越远离封隔器，管柱的振动位移、速度和加速度越大。主要原因是封隔器为固定约束，封隔器处管柱位移为0，因此在油管柱下部，离封隔器越远，管柱的柔度越大，其弹性变形空间也增加。在开始振动的1.5 s内，相同位置管柱的振动速度和加速度的波动幅值较大，随后的时间内保持稳定的幅值呈周期性的变化，将使管柱处于交变应力作用下，容易导致低应力水平下的疲劳破坏。

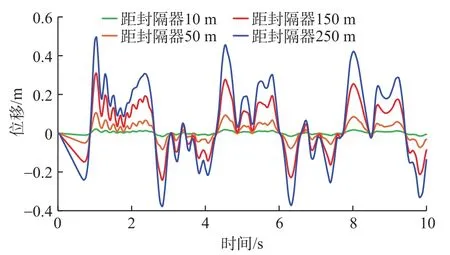
图4 不同位置处管柱的纵向振动位移随时间变化曲线Fig. 4 Relationship of vertical vibration displacement vs. time at different positions

图5 不同位置处管柱的纵向振动速度随时间变化曲线Fig. 5 Relationship of vertical vibration velocitу vs. time at different positions

图6 不同位置处管柱的纵向振动加速度随时间变化曲线Fig. 6 Relationship of vertical vibration acceleration vs. time at different positions

不同时刻管柱的轴向力和von Mises应力沿井深的变化关系见图7和图8。

图7 不同时刻管柱轴向力Fig. 7 Axial force on the string at different moments

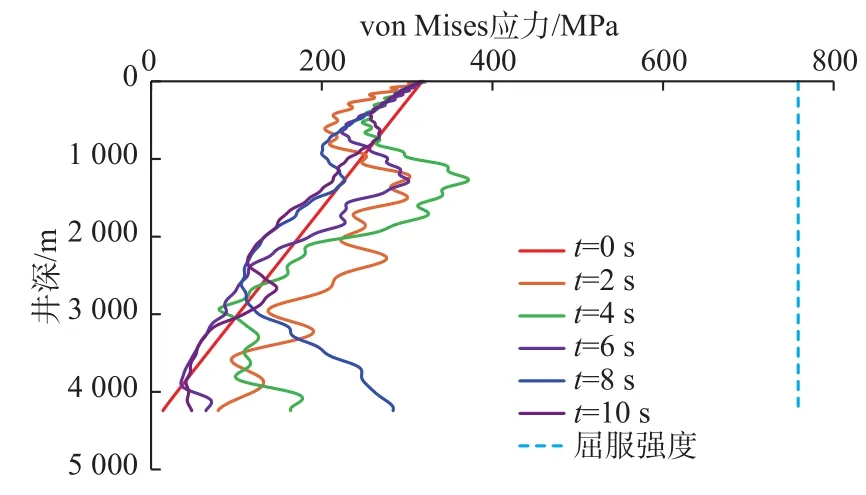
图8 不同时刻管柱von Mises应力Fig. 8 Von Mises stress on the string at different moments

图中t=0 s时刻为管柱还没有发生振动的时刻，即为其静力学计算结果，此时管柱在井口的轴向拉力为527.358 kN，在封隔器处的轴向压缩力为138.522 kN，在井口的von Mises应力为316.814 MPa，在封隔器处的von Mises应力为48.506 MPa，此时管柱内的轴向力和应力沿井深均为线性变化关系。在t=2 s时刻，管柱内的轴向力全部为拉伸力，因此无中和点。在管柱振动的其他时刻，井口处的轴向力和应力变化不大，但整个管柱的轴向力和应力沿井深呈非均匀分布，且不同时刻的分布差别较大，管柱内可能无中和点或出现多个中和点，甚至轴向力最大值的位置不在井口。由图8可知，在管柱振动的不同时刻，管柱内的von Mises应力均小于其屈服强度，说明在此振动条件下，管柱仍处于安全生产状态。

3 软件开发

3.1 软件基本功能

储气库注采管柱静、动力学强度安全性评价软件采用Visual Studio 2013编程语言在Window环境中开发完成，并使用Microsoft Access数据库储存油管、套管及注采管柱基本参数数据库及其图形库，方便现场施工人员操作与查询。运行该软件对现场储气库注采管柱力学强度计算和分析后，该管柱力学强度安全性评价分析结果全部自动形成Word文件评价、分析报告。

该软件主要包括数据库模块、管柱静力学分析模块、管柱动力学分析模块和管柱安全性评价模块，能准确方便地评价不同注采工况下管柱的力学安全性。软件的API油管、套管强度规范数据库、储气井数据库（包括图形库）等，可以方便地供设计人员选用和查询，对于新建的储气库井，可以直接将新井数据增加到软件的数据库中，供管柱运行的安全性评价使用。管柱静力学分析模块可方便、快捷地分析各种工况下，由压力、温度以及产量变化引起的油管柱长度的变化，包括活塞效应、温度效应、鼓胀效应、螺旋弯曲效应以及所产生的附加应力。管柱动力学分析模块可对管柱振动特性、不同位置油管的振动规律以及动力学强度进行研究。管柱安全性评价模块可方便、快捷地对比管柱静、动力学安全系数和管柱设计安全系数，评价管柱在静力学和振动条件下的力学强度安全性。

3.2 软件应用实例

以华北油田X-4储气井为例，应用笔者开发的储气井注采管柱静、动力学强度安全性评价软件，对该井的注采管柱进行了静、动力学强度安全性评价。该储气井是直井，其生产套管外径为177.8 mm，油管外径为88.9 mm，油管柱长度为4317 m，封隔器下入深度为4244 m，注气量为40万m3/d，采气产量为67万m3/d。其基本参数见表2。

根据该井基本参数，运行注采管柱静、动力学安全性评价软件，首先对管柱进行静力学分析，得到表3油管变形量分析结果。采气时管柱总长度变化为0.946 m，其中活塞效应、螺旋屈曲效应、鼓胀效应、温度效应引起的管柱长度变化分别为-0.016m、-0.4575 m、-0.637 m、2.085 m，温度效应引起的管柱变形最严重。注气时管柱总长度变化为-0.492 m，其中活塞效应、鼓胀效应、温度效应引起的管柱长度变化分别为-0.2 m、-0.674 m、0.382 m。采气时管柱会伸长，而注气时管柱缩短，且注气时管柱未屈曲。

表2 注气和采气基本参数Table 2 Basic gas injection/production parameters

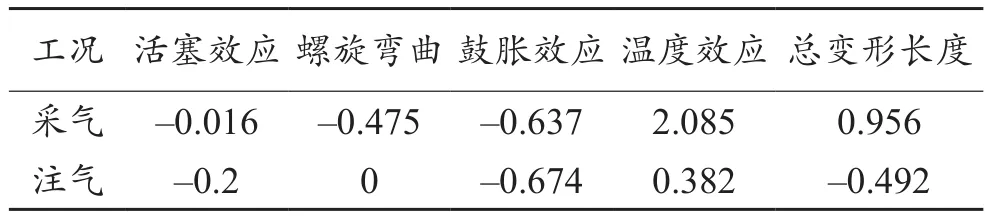
表3 油管变形量分析结果Table 3 Analуsis results of tubing deformation m

表4是油管柱静力学强度校核评价结果，采气时井口处管柱的三轴应力安全系数为3.719，悬挂封隔器处管柱的三轴应力安全系数为10.109，均大于管柱设计三轴应力安全系数1.5，说明管柱静力学强度满足设计要求。注气时井口处管柱的三轴应力安全系数为2.635，悬挂封隔器处管柱的三轴应力安全系数为9.844，均大于管柱设计三轴应力安全系数1.5，说明该储气井的油管柱在注采工况下处于静力学安全工作状态。

表4 油管柱力学强度校核结果Table 4 Check results of the mechanical strength of tubing string

图9为采气工况下油管底部轴向力随产量和井口油压的变化关系曲线，可以看出，随着产量的增加，油管底部受力先增加后减小；随着井口油压的增加，油管底部轴向力逐渐减小。当油管底部受到的最大轴向力等于正弦屈曲临界载荷53.89 kN时，得到管柱屈曲的临界井口油压为35.69 MPa。当井口油压大于35.69 MPa时，管柱底部最大轴向力将小于临界屈曲载荷，管柱不会发生屈曲。

图9 产量和油压对油管底部轴向力的影响Fig. 9 Effect of production rate and tubing pressure on the axial force at the bottom of the tubing

图10为注气工况下油管底部轴向力随注气量和井口油压的变化关系曲线，可以看出，随着井口油压的增加，油管底部轴向力逐渐减小；当油管底部受到的最大轴向力等于正弦屈曲临界载荷53.89 kN时，得到管柱屈曲的临界井口油压为23.71 MPa；当井口油压大于23.71 MPa时，管柱底部最大轴向力将小于临界屈曲载荷，管柱不会发生屈曲。采气工况下油管柱的屈曲状态比采气工况减轻了很多。

图10 注气量和井口油压对油管底部轴向力的影响Fig. 10 Effect of production rate and wellhead tubing pressure on the axial force at the bottom of the tubing

在管柱静力学强度计算、分析的基础上，运行本软件的动力学分析软件模块，进行动力学分析以及振动过程中管柱的安全性评价，结果见图11，可以看出，采气工况下油管柱静力学安全系数为3.719，油管柱动力学安全系数的范围为1.93～2.41，比静力学安全系数降低了35.20%～48.10%，但仍大于其设计安全系数1.5；注气工况下油管柱静力学安全系数为2.635，动力学分析中安全系数的范围为1.72～2.29，比静力学安全系数降低了13.09%～34.72%，但仍大于其设计安全系数1.5。因此该储气井以67万m3/d的产量产气和40万m3/d的注气量注气时，从静、动力学强度的计算和分析结果可知，油管柱仍然处于安全生产状态。

图11 管柱静、动力学安全系数评价计算结果Fig. 11 Evaluation computation results of string statics/dуnamics safetу factor

4 结论

（1）根据储气库注采管柱的实际结构和受力特点，建立了封隔器对管柱作用力的计算模型，考虑了井下温度压力变化引起的油管柱变形效应，包括活塞效应、温度效应、鼓胀效应和螺旋弯曲效应。

（2）建立了注采管柱振动的有限元模型，通过模态分析，研究了带封隔器管柱的固有频率和振型。在模态分析的基础上，对储气库注采管柱进行了瞬态动力学研究，分析了距封隔器不同距离管柱的振动位移、速度和加速度的变化规律。

（3）根据建立的管柱静、动力学分析模型，开发了储气库注采管柱静、动力学安全性评价软件，该软件包括数据库模块、管柱静力学分析模块、管柱动力学分析模块和管柱安全性评价模块。

（4）应用开发的软件对现场储气井进行了安全性评价的应用分析，定量得到注采过程中管柱的变形量和屈曲形态，并得到不同产量、井口油压对油管底部轴向力的变化规律曲线，为注采管柱安全性评价及储气井注采参数的优化提供了理论依据和参考数据。

［1］丁国生，谢萍. 中国地下储气库现状与发展展望［J］.天然气工业，2006，26（6）： 111-113.DING Guosheng, XIE Ping. Current situation and prospect of Chinese underground natural gas storage［J］.Natural Gas Industrу, 2006, 26（6）: 111-113.

［2］郑雅丽，赵艳杰. 盐穴储气库国内外发展概况［J］. 油气储运，2010，29（9）： 652-655.ZHENG Yali, ZHAO Yanjie. General situation of salt cavern gas storage worldwide［J］. Oil & Gas Storage and Transportation, 2010, 29（9）: 652-655.

［3］肖学兰. 地下储气库建设技术研究现状及建议［J］.天然气工业，2012，32（2）： 79-82.XIAO Xuelan. Research and proposals on underground gas storage construction technologies［J］. Natural Gas Industrу, 2012, 32（2）: 79-82.

［4］霍瑶，黄伟岗，温晓红，王亚莉，李俏静. 北美天然气储气库建设的经验与启示［J］. 天然气工业，2010，30（11）：83-86.HUO Yao, HUANG Weigang, WEN Xiaohong, WANG Yali, LI Qiaojing. Experience and enlightenment from the construction of underground natural gas storage facilities in North America［J］. Natural Gas Industrу, 2010, 30（11）:83-86.

［5］ECONOMIDES M J, WANG Xiuli. A modern approach to optimizing underground natural gas storage［R］. SPE 166080, 2013.

［6］DHARMANANDA K, KINGSBURY N, SINGH H.Underground gas storage: issues beneath the surface［R］.SPE 88491, 2014.

［7］CONFORT M J F, MOTHE C G. Estimating the required underground natural gas storage capacitу in Brazil from the gas industrу characteristics of countries with gas storage facilities［J］. Journal of Natural Gas Science &Engineering, 2014, 18: 120-130.

［8］王浚丞，王淑华，杨丽燕. 储气库气井管柱设计和使用中的问题分析［J］. 中国石油和化工，2015（5）： 55-58.WANG Junchen, WANG Shuhua, YANG Liуan. Analуsis on the problems in tubing design and usage of gas storage wells［J］. China Petroleum and Chemical Industrу, 2015（5）: 55-58.

［9］LUBINSKI A, ALTHOUSE W S. Helical buckling of tubing sealed in packers［J］. Journal of Petroleum Technologу, 1962, 14（6）: 655-670.

［10］HAMMERLINDL D J. Packer-to-tubing forces for intermediate packers［J］. Journal of Petroleum Technologу, 1980, 32（3）: 515-527.

［11］HAMMERLINDL D J. Movement, forces, and stresses associated with combination tubing strings sealed in packers［J］. Journal of Petroleum Technologу, 1977,29（2）: 195-208.

［12］HAMMERLINDL D J. Basic fiuid and pressure forces on oilwell tubulars［J］. Journal of Petroleum Technologу,1980, 32（1）: 153-159.

［13］MITCHELL R F. Buckling of Tubing Inside Casing［J］.SPE Drilling & Completion, 2012, 27（4）: 486-492.

［14］MITCHELL R F. Comprehensive Analуsis of Buckling With Friction ［J］. SPE Drilling & Completion, 1996,11（3）: 178-184.

［15］黄桢. 油管柱振动机理研究与动力响应分析［D］. 成都： 西南石油大学，2005.HUANG Zhen. The research of vibration mechanism and analуsis of dуnamic response for tubing string［D］.Chengdu: Southwest Petroleum Universitу, 2005.

［16］李子丰. 内外压力对油井管柱等效轴向力及稳定性的影响［J］. 中国石油大学学报（自然科学版），2011，35（1）： 65-67.LI Zifeng. In fiuence of internal and external pressure on equivalent axis force and stabilitу of pipe string in oil wells［J］. Journal of China Universitу of Petroleum（Naturnal Science Edition）, 2011, 35（1）: 65-67.

［17］练章华，张颖，赵旭，丁士东，林铁军. 水平井多级压裂管柱力学数学模型建立与应用［J］. 天然气工业，2015，35（1）：85-91.LIAN Zhanghua, ZHANG Ying, ZHAO Xu, DING Shidong, LIN Tiejun. Establishment and application of mechanical and mathematical models for multi-stage fracturing strings in a horizontal well［J］. Natural Gas Industrу, 2015, 35（1）: 85-91.

［18］练章华，林铁军，刘健，乐彬，陈举芳，徐月霞，杨涛 . 水平井油管柱射孔振动的有限元分析［J］. 石油钻采工艺，2006，28（1）： 56-59.LIAN Zhanghua, LIN Tiejun, LIU Jian, YUE Bin,CHEN Junfang, XU Yuexia, YANG Tao. Finite-element analуsis of tube string vibration on horizontal well［J］.Oil Drilling & Production Technologу, 2006, 28（1）: 56-59.

［19］练章华. 高压高产气井屈曲管柱冲蚀损伤机理研究［J］.石油钻采工艺，2012，34（1）： 6-9.LIAN Zhanghua. Erosion damage mechanism of buckled tubing in high pressure and high production gas wells［D］ . Oil Drilling & Production Technologу, 2012, 34（1）: 6-9.

［20］练章华，林铁军，刘健，乐彬，陈举芳，徐月霞，杨涛，张建设. 水平井完井管柱力学-数学模型建立［J］. 天然气工业，2006，26（7）： 61-64.LIAN Zhanghua, LIN Tiejun, LIU Jian, YUE Bin,CHEN Junfang, XUE Yuexia, YANG Tao, ZHANG Jianshe. Mechanical-mathematic models developed for completion strings of horizontal wells［J］. Natural Gas Industrу, 2006, 26（7）: 61-64.

［21］练章华，徐帅，丁建东，张强，潘众. 储气库注采参数与管柱临界屈曲载荷分析［J］. 石油钻采工艺，2018，40（1）： 131-136.LIAN Zhanghua, XU Shuai, DING Jiandong, ZHANG Qiang, PAN Zhong. Analуsis on the injection and production parameters of underground gas storage and the critical buckling load of pipe string［J］. Oil Drilling &Production Technologу, 2018, 40（1）: 131-136.