Combined Size and Shape Optimization of Structures with DOE, RSM and GA

Jie Song, Hongliang Hua, Zhenqiang Liao, Tao Wang and Ming Qiu(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

The natural frequencies of a structure are the fundamental parameters affecting the dynamic behavior of the structure. Hence, some limitations should be imposed on the ranges of natural frequencies to reduce the domain of vibration and also to prevent the resonance phenomenon in the dynamic response of structures[1]. Accordingly, structures should be iteratively analyzed and designed to achieve this purpose. Recently, the problem of structure’s eigenfrequencies and eigenmodes optimization has attracted considerable interests[2-6]. One of the most frequently used shape optimization method, in engineering design, is describing the structure boundary based on non-uniform rational B-spline (NURBS) mathematically[7-9]. Each NURBS is parameterized by a finite set of control points, and the coordinates of NURBS control points are moved as optimization variables in this method. So far as known to the authors, many studies have employed NURBS in solving 2-D or regular structure shape optimization problems[9-11]. However, it is not so easy for users to achieve parameterization of a complexity structure using NURBS, and this is why there is little information available in literature about 3-D and irregular structure shape optimization problems using NURBS. In addition to this, geometry alteration is usually carried out by removing mesh elements and remeshing at each iteration (size or shape optimization) rather than moving their nodes. Therefore, the finite element analysis (FEA) remodeling will occupy a substantial portion of optimization time. In order to achieve fast parameterization and modification of complexity structure, we propose to use a novel mesh morphing technique to achieve the optimization of a machine gun system.

This paper therefore emphasizes a way to maximize (or minimize) the structure natural frequencies by combined size and shape optimization with aids of a novel mesh morning technique, design of experiments (DOE), response surface method (RSM), genetic algorithm (GA). This remainder of the paper is structured as follows. Section 1 describes the design of the machine gun system optimization model. Section 2, DOE sampling, RSM and GA optimization are presented. Section 3 analyzes the dynamics of the machine gun system (initial design and optimal design) to investigate the efficacy of the shape optimization. Section 4 finally concludes the paper.

1 Optimization Description of the Machine Gun System

The optimization of machine gun system aims to improve its firing accuracy by increasing main vibration mode frequency without material addition (mass).

1.1 Objective functions

The vibration problems for the machine gun system have long been a subject for research. The barrel vibration can affect the accuracy of firing guns due to the up and down jump during projectile launch[12-13]. For this reason, our work is motivated to optimize the machine gun system structure to improve its firing accuracy.

In this study, model analysis of the machine gun was conducted through the use of hypermesh. In the modeling process, the machine gun is constrained at the bottom of the three tripods as shown in Fig.1. The material of the modal analysis is assumed to be steel of Young’s modulus 210 GPa, with a density of 7 800 kg/m3and a Poisson’s ratio 0.3. The results of FE analysis are in close agreement with experimental tests as shown in Tab.1.

The frequency of the main vibration mode of the machine gun system in this paper is 14.56 Hz (2nd mode),for details, can refer to Ref. [14]. And the firing frequency (exciting frequency) is 10 Hz. Maximizing the frequency of the main vibration mode could guarantee a resonance-free frequency band above the exciting frequency. This makes the machine gun system to have more damping periods before next firing, and the disturbances of the bullets will achieve more stable with little fluctuations. Therefore, the frequency of the main vibration mode (2nd mode) is taken as the objective function for optimization in this case. It should be noted that in experimental tests, the exciting force is applied in the vertical direction, therefore, only the 2nd and the 4th mode are obtained.

Fig.1 Finite element model

Tab.1 Validation of the finite element model

1.2 Design variables

1.2.1Mesh morphing

In order to achieve parameterization of the tripods radian, a novel mesh morphing technique is introduced to change the geometry of the finite element model. Mesh morphing is a process of gradually transforming one source mesh into another target mesh by changing the coordinates of nodes without changing the number of nodes or elements after mesh morphing, while the connections between these nodes or elements remain unchanged. It is not necessary to rebuild the finite element model using mesh morphing technology, because only the mesh model is changed, while the material properties and boundary conditions remain unchanged. In order to apply the mesh morphing technology, we first designate these elements to be transformed as a “domain” controllable by some nodes to record the source mesh and target mesh[15]. The shape design variable is generated by

(1)

C=C+αS

(2)

whereC={c1,c2,…,cn} are coordinates of the nodes;S={s1,s2,…,sn} denotes the shape design variables.

1.2.2Design variables

Design variables, such as the rib thickness (T1,T2,T3) of the barrel, tripod wall thickness (T4,T5) and tripod radian (S1,S2,S3) (see Fig.2) will be used to achieve the optimization of the machine gun system and improve its target mode frequency.

Fig.2 Design variables

1.3 Optimization model

In order to maximize the frequency of the main vibration mode (F) of the machine gun system, the rib thickness (T1,T2,T3) of the barrel, tripod wall thickness (T4,T5) and tripod radian (S1,S2,S3) were optimized simultaneously as design variables to ensure that the structure mass(M) is not affected, as shown below:

Maximize:

F(T1,T2T3,T4,T5,S1,S2,S3)

(3)

Subject to:

(4)

2 Optimization Based on Response Surface

The flow chart shown in Fig.3 explains the proposed methodology. In DOE and RSM modules, the approximation of the optimization function is obtained. Based on this approximate function, the GA module is adopted to obtain the optimal results.

2.1 DOE sampling

2.1.1Hammersley sequence sampling

Since Hammersley sequence can produce fairly uniform point distributions in the design space. In this study, we propose to adopt Hammersley sequence sampling for creating nearly orthogonal and excellent space-filling designs[16]. Hammersley sequence sampling generates a set ofNpoints using the radix-Rnotation of an integer. That is, a specific integerpin radix-Rnotation can be represented as

(5)

wherem=[logRp]=[lnp/lnR] and the square brackets denote the integer portion of the number inside the brackets. The inverse-radix-number function constructs a unique number on the interval [0, 1] by reversing the order of the digits ofparound the decimal point. The inverse-radix-number function is

(6)

Finally, the Hammersley sequence ofM-dimensional points is generated as

(7)

wherep=0,1,2,…,N-1; and the values forR1,R2,…,Rm-1are the firstM-1 prime numbers 2,3,5,7,11,13,17,19,…. This approach generates a set ofNpoints in theM-dimensional design space [0,1]M. Finally, the [0,1]Mis mapped to the real design spaceXDby

XD=(xu-xl)XM(p)-abs(xl)

(8)

wherexlandxuare the lower and upper limits of the design variables. The Hammersley sequence sampling matrix is then embedded into FEM solving files in each run using secondary development technique and the responses (mass and frequency) are then obtained in Tab.2.

Fig.3 Flowchart of analysis

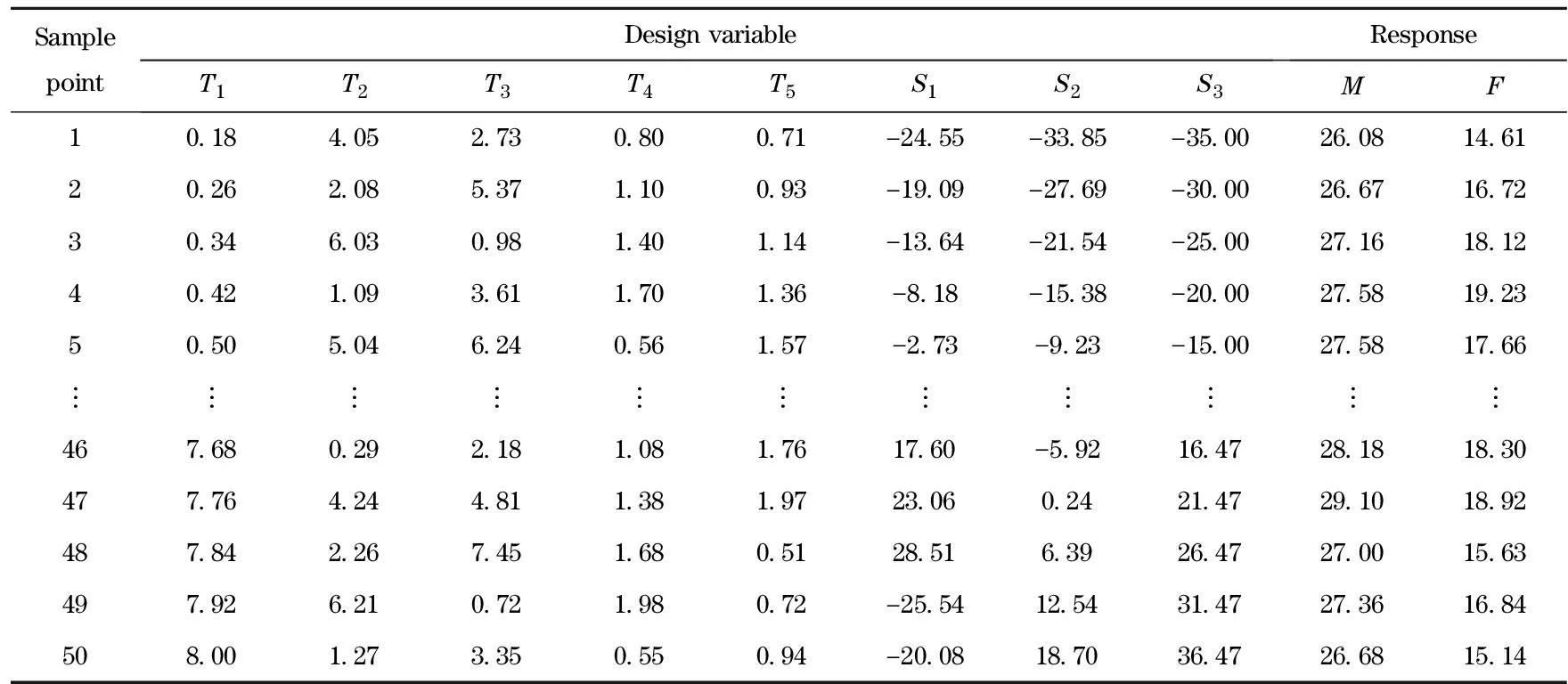
Tab.2 Hammersley sequence sampling and obtained responses

2.1.2Latin hypercube designs (LHD)

In order to verify the response surface accuracy, ten additional sample points which are different from Hammersley sequence sampling points are then generated. The maximin LHD is frequently adopted to generate evenly spread sample points in applications, see Refs.[17-19]. Formally, letX=(x1,…,xN),xi∈{0,…,N-1}k,i=1,…,N, thenXcan be represented as

(9)

where each row corresponds to a design point and each column corresponds to a component and is a permutation of the integers 0,1,…,N-1. Then let

(10)

Be the minimal distance inX(with respect to some distanced). A maximin LHD is a solution of the following problem:

(11)

The sample points are then obtained in Tab.3 by maxmin optimality for LHD in MATLAB.

The relative error of the response surface is given by

(12)

whereRRandR0denote the responses (mass and frequency) from the response surface and FEM solving. Tab.3 shows that the response surface has little error.

Tab.3 Latin hypercube designs and relative errors

2.2 RSM

Among the available meshless approximation schemes, the moving least squares (MLSM) method[20]is generally considered to be one of the best methods to approximate random data with a reasonable accuracy, because of its completeness, robustness and continuity[21-22]. With the MLSM approximation, the unknown functionφis approximated by

(13)

where PT(X) is a polynomial basis in the X space coordinates, andmis the total number of the terms in the basis.a(X) is the vector of coefficients and can be obtained by minimizing a weighted discreteL2norm as follows

(14)

(15)

Minimization of Eq.(14) with respect to the coefficientsa(X) leads to:

φ(X)=PT(X)A-1(X)B(X)φh

(16)

where

(17)

and

B(X)=[w1(X-X1)P(X1),w2(X-X2)P(X2),…,
wn(X-Xn)P(Xn)]

(18)

Eq.(16) can be written in the following compact form:

φ(X)=NT(X)φh

(19)

Leading to the definition of MLSM shape function which is defined as

NT(X)=PT(X)A-1(X)B(X)

(20)

where NT(X) contains the MLSM shape functions of nodes at point X.

2.3 GA

A genetic algorithm is an evolutionary optimization method which is inspired by the natural evolution of chromosomes during mating. In large spaces, where traditional optimization techniques can hardly deal with the problem, or are only able to find local optima, a GA is capable of locating the optimal solution in complex landscapes. GA has been shown to perform well in problems where the landscape is complex, noisy, time varying or has many local optima[23]. To do systematic tuning of the machine gun system, the GA is a powerful optimization algorithm. In this article, the GA optimization method is utilized for maximizing the natural frequency of the machine gun system. In our optimization, the population size of the GA is 20 and the maximum iterations is 30.

2.4 Results discussion

Fig.4 shows the iteration history of the design variables. Through the optimization:T1,T2,T3=0 mm, removing the stiffener from the gun barrel structure can increase the frequency of the main vibration mode of the machine gun system. Taking mechanical processing manufacturability into consideration,T4=1.5 mm andT5=1 mm are considered to be the optimal solution in this case. The optimal tripod radian parameters,S1=4 mm,S2=40 mm,S3=-32 mm, are all acceptable in engineering.

Fig.4 Iteration history of design variables

Fig.5 shows that the optimal machine gun system achieves about a 31.0% increment in the main vibration mode eigenfrequencies. The machine gun system is then redesigned according to the optimal structure parameters and the new design is shown in Fig.6b.

Fig.5 Iteration history of objective functions

3 Dynamic Analysis and Firing Accuracy Improvement

To investigate the optimization efficacy on firing accuracy, two rigid-flexible coupling multi-body dynamic models are then established. These two models used to verify that the firing accuracy improvement are essentially the same, except for the tripod structure and gun barrel (initial design and optimal design, Fig. 6). This ensured that any changes in the vibration response should be directly attributable to the tripod and gun barrel structures, and not changes in simulation setup. Since the bullets dispersion is directly affected by the muzzle dynamic response, and the muzzle vibration response mainly occurs in theY-Zplane[12,24]. Fig.7 shows that the bullets perturbations of the optimal machine gun system achieve more stable with little fluctuations during firing compared with the initial design.

Fig.6 Machine gun system modeled by UG

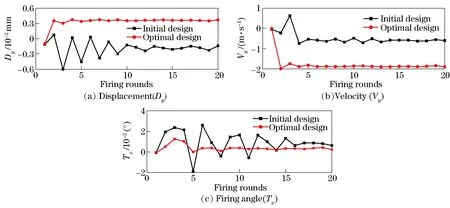
Fig.7 Firing dynamic response of muzzle

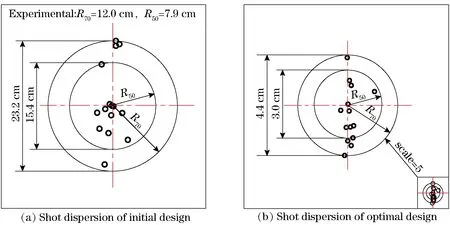
Fig.8 Shot dispersion

Based on the muzzle dynamic response, the exterior ballistics calculations confirmed the improvement of machine gun firing accuracy . The firing accuracy is obtained (Fig. 8) via solving exterior ballistics differential equations[25]by MATLAB programming.R50,R70are the radius of the dispersions circles, which 50% and 70% of the bullets are enclosed within. The exterior ballistics calculation and experimental tests of the initial machine gun system show good agreement in Fig.8a.R50,R70of the optimal design were reduced by 80.5% and 81.0%, respectively, compared with that of the initial design. This is due to the machine gun system achieved high stability during firing. The new designed tripod and gun barrel structure can effectively improve the machine gun firing accuracy.

4 Conclusions

A new combined size and shape optimization method for structural optimization problems is presented. Aim of this work is to maximize the main vibration mode of a machine gun system. Therefore a novel and flexible mesh morphing technique is employed to achieve fast parameterization and modification of complexity structure. The results of the rigid-flexible coupling dynamic analysis shows that bullet perturbations of the optimal machine gun system become more stable with little fluctuations during firing compared with the initial design. Based on the results of exterior ballistics calculation,R50,R70of the optimal design were reduced by 80.5% and 81.0%, respectively.

The proposed method for machine gun system design process, is relatively time-saving, reliable and it can also be applicable to solve similar problems.

[1] Shen J L, Wang G Q, Bi Q S, et al. A comprehensive genetic algorithm for design optimization of Z-bar loader working mechanism[J]. Journal of Mechanical Science and Technology, 2013, 27(11):3381-3394.

[2] Jensen J, Pedersen N. On maximal eigenfrequency separation in two-material structures: the 1D and 2D scalar cases[J]. Journal of Sound and Vibration, 2006, 289(4-5):967-986.

[3] Yoon G. Structural topology optimization for frequency response problem using model reduction schemes[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(25-28):1744-1763.

[4] Maeda Y, Nishiwaki S, Izui K, et al. Structural topology optimization of vibrating structures with specified eigenfrequencies and eigenmode shapes[J]. International Journal for Numerical Methods in Engineering, 2006, 67(7):597-628.

[5] Montealegre Rubio W, Paulino G, Nelli Silva E. Tailoring vibration mode shapes using topology optimization and functionally graded material concepts[J]. Smart Materials and Structures, 2011, 20(2):25009-25017.

[6] Nakasone P, Silva E. Dynamic design of piezoelectric laminated sensors and actuators using topology optimization[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(16):1627-1652.

[7] Nasuf A, Bhaskar A, Keane A J. Grammatical evolution of shape and its application to structural shape optimisation[J]. Structural and Multidisciplinary Optimization, 2013, 48:187-199. DOI:10.1007/S00158-013-0890-0.

[8] Schramm U, Pilkey W D. The coupling of geometric descriptions and finite elements using NURBs:a study in shape optimization[J]. Finite Elements in Analysis and Design, 1993, 15(1):11-34.

[9] Silva C A C, Bittencourt M L. Velocity fields using NURBS with distortion control for structural shape optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33:147-159. DOI:10.1007/S00158-006-0046-6.

[10] Azegami H, Fukumoto S, Aoyama T. Shape optimization of continua using NURBS as basis functions[J]. Structural and Multidisciplinary Optimization, 2013, 47:247-258. DOI: 10.1007/S00158-012-0822-4.

[11] Clune R, Kelliher D, Robinson J, et al. NURBS modeling and structural shape optimization of cardiovascular stents[J]. Structural and Multidisciplinary Optimization, 2014, 50(1):159-168.

[12] Gimm H, Cha K, Cho C. Characterizations of gun barrel vibrations of during firing based on shock response analysis and short-time Fourier transform[J]. Journal of Mechanical Science and Technology, 2012, 26(5):1463-1470.

[13] Littlefield A, Kathe E, Durocher R. Dynamically tuned shroud for gun barrel vibration attenuation[C]∥Smart Structures and Materials 2002: Damping and Isolation, 2002, 4697:89-97.

[14] Hua H, Liao Z, Song J. Vibration reduction and firing accuracy improvement by natural frequency optimization of a machine gun system[J]. Journal of Mechanical Science & Technology, 2015, 29(9):3635-3643.

[15] Liu W, Yang Y. Multi-objective optimization of an auto panel drawing die face design by mesh morphing[J]. Computer-Aided Design, 2007, 39(10):863-869.

[16] Qazi M, He L, Mateen P. Hammersley sampling and support-vector-regression-driven launch vehicle design[J]. Journal of Spacecraft and Rockets, 2007, 44(5):1094-1106.

[17] Alam F, McNaught K, Ringrose T. A comparison of experimental designs in the development of a neural network simulation metamodel[J]. Simulation Modelling Practice and Theory, 2004, 12(7-8):559-578.

[18] den Hertog D, Stehouwer P. Optimizing color picture tubes by high-cost nonlinear programming[J]. European Journal of Operational Research, 2002, 140(2):197-211.

[19] Rikards R, Auzins J. Response surface method for solution of structural identification problems[J]. Inverse Problems in Science and Engineering, 2004, 12(1):59-70.

[20] Kahhal P, Brooghani S Y A, Azodi H D. Multi-objective optimization of sheet metal forming die using FEA coupled with RSM[J]. Journal of Mechanical Science and Technology, 2013, 27(12):3835-3842.

[21] Onate E, Perazzo F, Miquel J. A finite point method for elasticity problems[J]. Computers & Structures, 2001, 79(22-25):2151-2163.

[22] Yang X, Dai B, Zhang W. The complex variable meshless local Petrov-Galerkin method of solving two-dimensional potential problems[J]. Chinese Physics B, 2012, 21(10):49-55.

[23] Swarnalatha A, Shanthi A. Optimization of single variable functions using complete hardware evolution[J]. Applied Soft Computing, 2012, 12(4):1322-1329.

[24] Shi Y, Wang D. Multi-body modeling and vibration analysis for gun[C]∥2009 IEEE International Conference on Intelligent Computing and Intelligent Systems Proceedings, 2009(2):636-640.

[25] Li J, Liao Z, Li H, et al. Simulation of fire density of Gatling gun shooting on light tripod[J]. Journal of Nanjing University of Science and Technology, 2013, 37(2):209-214.