基于广义层间位移角谱的复合自复位结构体系的参数分析
武大洋 吕西林
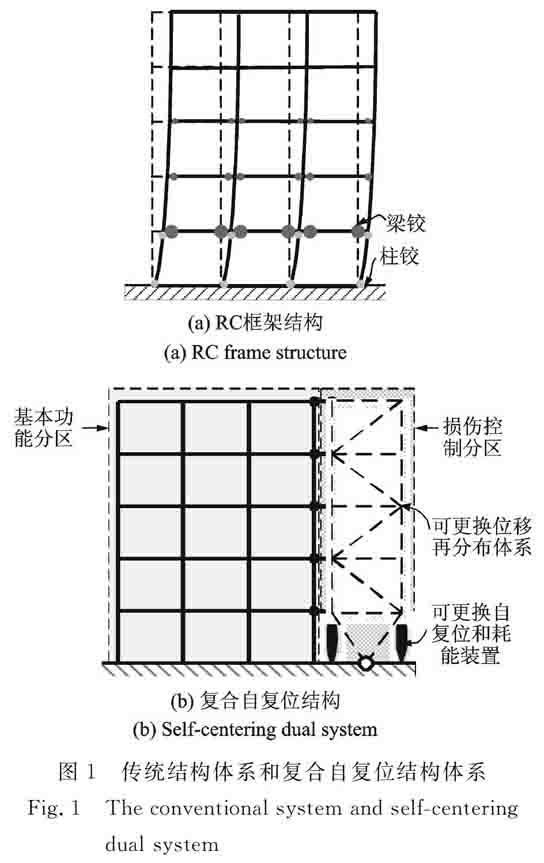


摘要: 提出了复合自复位结构体系,该结构体系在层次上由基本功能分区和损伤控制分区组成。根据不同分区的结构变形特征将复合自复位结构体系简化为由剪切梁和弯曲梁组成的双梁分布体系模型。求解得到复合自复位结构体系振型方程的闭合解,分析该体系在不同剪弯刚度比和弯曲梁与其底部约束刚度比下振型和振型转角的变化规律。基于振型叠加法得到体系的广义层间位移角谱,分析了剪弯刚度比和弯曲梁与其底部约束刚度比、阻尼比和高阶模态对体系广义层间位移角谱的影响。结果表明:在剪弯刚度比介于1~3的区间,弯曲梁与其底部约束刚度比介于1~5的区间,通过附加一定的阻尼,体系不仅可以抑制高阶振型的影响得到较均匀的层间位移分布而且可以降低最大响应。以广义层间位移角谱为工具,可以实现复合自复位结构体系直接基于位移的设计。
关键词: 抗震结构; 复合体系; 自复位结构; 双梁模型; 广义层间位移角谱
中图分类号: TU352.1 文献标志码: A 文章编号: 1004-4523(2018)02-0255-10
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.008
引 言
复合自复位结构体系将地震作用下输入结构的能量集中于可更换的耗能构件中,使结构构件在震后可以无需修复继续使用,降低结构功能中断时间以实现震后可恢复功能的更高目标。为达到上述目标,Pettinga等[1]将弹性框架作为恢复力机制与主结构组成复合体系,既可以降低结构的残余位移又可以增加结构抵抗地震作用的能力;Terán-Gilmore等[2]将弹性抗弯框架与带有屈曲约束支撑(Buckling-Restrained Brace, BRB)的框架组合,利用弹性框架作为自复位机制消除由于BRB屈服引起的残余位移取得了较好的控制效果。由此可见利用弹性框架作为实现自复位的策略可以有效地降低结构的残余位移,避免了使用预应力或者后张拉装置带来的施工和维护上的复杂性;并且这种双抗力的复合结构体系可以提高结构的冗余度和鲁棒性(称之为复合I型)。
与附加底部与基础固接的弹性框架组成复合体系不同,MacRae等[3]研究发现钢框架结构中的摇摆重力柱可以有效降低结构在地震作用下的层间位移集中现象,降低结构出现局部薄弱层破坏的可能性。将底部与基础铰接的附加摇摆机构与主结构组合成复合体系,利用附加的摇摆体约束主结构的变形模式,使得主结构的层间位移角在地震作用下产生重分布,降低层间位移角的局部集中程度,避免因局部损伤过于严重而导致结构整体失效(称之为复合Ⅱ型)。曲哲等[4]将摇摆墙、金属阻尼器与框架结构组合使用,不仅降低了结构的响应而且使得结构的层间位移角分布趋于均匀;吴守君等[5]分析了框架-摇摆墙结构的受力特点,提出了摇摆墙加固的具体方法以及连接的局部构造。Qu等[6]将底部铰接的Rocking Cores与中心支撑钢框架(Concentrically Braced Frames, CBFs)组合在一起,利用Rocking Cores限制CBFs的层间位移集中程度。因此利用底部与基础铰接的摇摆体可以有效地控制结构的层间位移集中程度,降低结构局部的位移需求,避免因局部过度损伤而使结构退出工作。
根据上述分析可以发现,底部固结的弹性框架可以作为自复位机制降低主结构的残余位移,而底部铰接的摇摆墙或者摇摆框架可以通过层间位移的重分布限制结构的局部层间位移集中程度。为将复合体系的这两个机制集成到一个体系中,杜永峰和武大洋[7]提出一种新型复合体系,RC框架-自复位消能摇摆刚架。与上述文献中体系不同,自复位消能摇摆刚架与基础的连接为弹性转动约束,通过底部两个耦合的自复位阻尼器实现可更换的耗能机制,既可以消除残余位移又可以限制结构的层间位移集中,是一种效率较高的复合体系。本文以上述研究[7-8]为基础,将RC框架拓展为一般的框架结构体系,与自复位消能摇摆刚架组成复合自复位结构体系(称之为复合Ⅲ型)。
复合体系的设计及其限制层间位移集中程度的评估,需要将体系的变形模式引入到性能指标中,而传统的基于单自由度体系的反应谱给出的是结构整体的反应指标,无法反映结构沿高度的层间位移角的变化趋势。再者,单自由度体系的反应谱也无法反映高阶模态对体系层间位移角需求的影响[9-10]。为克服反应谱的以上缺陷,Iwan[9]在1997年提出了量化体系位移角需求的指标:层间位移角谱(Interstory Drift Spectrum, IDS)。与传统的基于单自由度体系的反应谱不同,IDS是以连续剪切梁为数值模型,该模型最大的优点是可以将体系层间位移角沿高度的分布考虑其中,通过多模态的叠加考虑高阶振型对体系层间位移角的影响,可以更加准确地计算体系的最大层间位移角需求。Miranda和Akkar[10]将Iwan[9]提出的以连续剪切梁为模型的IDS拓展为广义层间位移角谱(Generalized Interstory Drift Spectrum, GIDS)。GIDS將连续剪切梁模型拓展为由剪切梁和弯曲梁组成的复合体系模型,通过改变剪切梁和弯曲梁之间的刚度比,该模型可以用来分析多种结构体系,包括剪切变形为主的结构、弯剪变形的结构和弯曲变形为主的结构。杨迪雄等[11]基于Miranda和Akkar[10]的成果,利用GIDS研究了弯剪型结构在近场脉冲型地震作用下层间位移沿结构高度分布的规律,证明GIDS可以有效反映体系的变形规律,为设计和评估体系提供一定的参考。
本文将复合自复位结构体系中的框架结构简化为底部固接的剪切悬臂梁,将自复位消能摇摆刚架简化为底部弹性约束的弯曲梁,由二者组成复合体系理论模型。通过求解该复合体系理论模型得到体系振型的闭合解,进而可以得到体系的GIDS。以剪切梁和弯曲梁刚度比、弯曲梁与基础转动弹簧的刚度比为参数,分析了复合体系在不同刚度比下的振型和振型转角的变化规律,以及复合自复位结构体系的层间位移角谱在两种刚度比、阻尼比和高阶振型下的变化规律。

