微分求积升阶谱有限元方法及其在薄板自由振动中的应用
伍洋 邢誉峰

摘要: 提出了一种基于Hermite插值的微分求积升阶谱有限元方法。单元在几何映射上采用了混合函数方法,而在形函数的构造上,单元边界上采用非均匀节点的Hermite插值基函数,单元内部升阶谱形函数的构造则采用雅克比正交多项式的张量积形式。将单元形函数与高斯-洛巴托积分法结合起来离散薄板的势能泛函从而得到相应的单元矩阵。提出的薄板单元在单元边界以及单元内部的节点配置完全自由,因而可以用于不同阶次的单元的连接。通过在薄板自由振动中的应用计算以及与精确解的对比,结果表明:提出的微分求积升阶谱有限元方法不仅计算精度高,而且收敛速度快,同时在阶次较高时仍然具有良好的数值稳定性。
关键词: 薄板自由振动; 微分求积方法; Hermite插值; 升阶谱有限元方法
中图分类号: O323; O241.82 文献标志码:A文章编号1004-4523(2018)02-0343-09
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.019
引言
有限元方法自从20世纪60年代被正式提出以来,目前已经广泛应用于工程实际中,并对促进经济发展,解决工程科学问题做出了巨大贡献[1-3]。其中,h-型有限元方法以其技术简单、成熟,目前已发展成为有限元分析的主流方法。通过加密网格,该方法理论上可以得到足够高精度的计算结果。然而,在实际计算过程中,h-型有限元方法的收敛速度一般较慢,高精度的计算结果往往需要非常精细的网格才能得到,因而对CAD系统的前处理过程要求更加严格。伴随着h-型方法发展的还有p-型有限元方法,这种方法在计算过程中可以保持网格划分不变,通过提高单元的阶次便可得到高精度的计算结果。Babuka 等从理论分析和实际应用表明p-型有限元方法具有比h-型方法更快的收敛速度[3-5]。作为一种典型的p-方法,升阶谱有限元方法以其独特的优势在有限元方法发展的早期得到了广泛的研究[6-9]。其最显著的特点是低阶单元的基函数是高阶单元基函数的子集,这样在计算过程中中,低阶单元的结构矩阵是高阶单元结构矩阵的子矩阵,即所谓“嵌套”特性。进而在单元阶次升高时,前一步的计算结果仍然可以保留,从而降低重复分析的成本。基于这些优势,该方法一直被认为是未来实现自适应分析的主流技术。然而,由于历史和该方法自身的技术困难,升阶谱有限元方法的应用始终未能得到足够的推广[10]。
传统升阶谱有限元方法的基函数一般不具有插值特性,从而导致节点自由度不具有明确的物理意义,这样使得单元的组装以及边界条件的施加都变得困难。另外,随着单元阶次升高,高阶(几十阶或更高)多项式的计算带来的数值稳定性问题一直是一个技术难题[8]。最近,相关学者提出了微分求积升阶谱有限元方法,并将其应用于Mindlin板的自由振动问题中[11]。与传统升阶谱方法不同,该方法在单元边界上采用了非均匀节点的插值基函数,而在单元内部则仍采用升阶谱面函数。这样使得单元组装和边界条件施加的问题得到了解决。此外, 该方法采用了正交多项式的迭代公式进行计算,有效地克服了高阶多项式计算的数值动荡特性。
基于微分求积升阶谱有限元方法的上述优点,本文将把该方法推广到C1型单元的构造上。单元边界的形函数的构造通过一维高阶Hermite插值函数与三次Hermite插值函数混合得到,而单元内部面函数的构造则通过Jacobi正交多项式的张量积形式得到。其中,单元边界节点数目配置自由,因此可以适用于不同阶次的单元拼接以及自适应分析中局部自由度的调整。由于单元边界插值基函数的节点分布将对结构矩阵的数值特性具有重要的影响,本文提出了一类非均匀节点,即Gauss-Jacobi点,将有助改善单元的数值稳定性。此外,研究表明这类非均匀节点具有稳定的插值特性,因此可作为微分求积方法(强形式)的非均匀节点使用。计算表明,本文提出的C1型微分求積升阶谱有限元方法具有精度高,收敛速度快等特点,在单元阶次较高时,仍然具有较好的数值稳定性。
第2期伍洋,等: 微分求积升阶谱有限元方法及其在薄板自由振动中的应用振 动 工 程 学 报第31卷1微分求积升阶谱薄板单元〖*2〗1.1一维Hermite插值基函数对给定定义在区间[-1,1]上的一维函数fξ,其Hermite插值近似函数为fξ≈H0ξf′-1+HN+1ξf′1+
∑Nj=1Hjξfξj=∑N+1j=0Hjξj(1)式中ξj, j=1~N为插值节点,边界上的基函数为H0ξ=1-ξ22L1ξ
H1ξ=c1ξ+c21-ξ2L1ξ
HNξ=c3ξ+c41+ξ2LNξ
HN+1ξ=ξ2-12LNξ(2)内部节点对应的基函数为Hjξ=1-ξ21-ξ2jLjξ, j=2,3,…,N-1(3)式中Lj(ξ),j=1~N,为定义在节点ξj的拉格朗日插值函数,而方程中常数项为:c1=12-L′1ξ1, c2=32-L′1ξ1,
c3=-12-L′NξN, c4=32+L′NξN(4)可以看到内部节点ξj, j=2~N-1对应的基函数Hj (ξ) 满足在该节点取值为1,而在其他节点处取值为0。然而Hj (ξ)在该节点的取值不一定为最大值,这样在节点数目较多时,其插值精度并不稳定,易出现龙格现象。为提高插值精度,令maxHjξ=Hjξj=1, j=2,3,…,N-1(5)这样得到一组关于节点ξj, j=2~N-1的非线性方程组,通过求解上述方程组可以得到一组非均匀分布的节点。计算表明,该非均匀节点为权值为(3, 3)的雅克比正交多项式J(3,3)N-2(ξ) 的0点,因而在本文中记为高斯-雅克比点。文献[12]给出了多种求解正交多项式0点的方法。图1给出了当N=2和N=10时的Hermite插值基函数。从图1(a)中可以看到其明显的插值特性,从图1(b)可以看到中间节点对应的基函数在该节点取最大值1。
图1Hermite插值基函数
Fig.1Hermite interpolation bases1.2几何映射
在传统h-型有限元方法中,复杂结构的几何形状可以通过大量单元(通常为直边单元)来近似表示而不至于引起特别大的误差。然而,本文所构造的单元属于p-型单元,因此在实际过程中单元的几何尺寸要比传统h-型单元尺寸大,无法靠大量的单元来逼近实际的求解域,进而要求单元本身能精确地表示几何形状。为此,本文将采用混合函数方法来构造精确的曲边单元,该方法在一般的有限元教材中可以查到[3]。如图2所示,曲边单元(右图)在边界上的曲线可以通过参考坐标系(左图)表示为
x=xi(ξ),y=yiξ,-1≤ξ≤1,i=1,3
x=xi(η),y=yiη,-1≤η≤1,i=2,4(6)
根据混合函数插值,从参考域(母单元)到物理域的几何映射可以表示为:xξ,η=1-η2x1ξ+1+ξ2x2η+1+η2x3ξ+图2单元节点配置与几何映射
Fig.2Element node collocation and geometric mapping
1-ξ2x4η-1-ξ1-η4X1-
1+ξ1-η4X2-1+ξ1+η4X3-
1-ξ1+η4X4(7)
yξ,η=1-η2y1ξ+1+ξ2y2η+1+η2y3ξ+
1-ξ2y4η-1-ξ1-η4Y1-
1+ξ1-η4Y2-1+ξ1+η4Y3-
1-ξ1+η4Y4(8)式中Xi,Yi,i=1~4为4个顶点的直角坐标。此外,在薄板单元中需要计算到二阶导数,因此需要用到如下链式法则:x
y=1JJ22-J12
-J21J11ξ
η,
J=J11J12
J21J22=xξyξ
xηyη(9)
2x2
2y2
2xy=1J2·
J222J212-2J12J22
J221J211-2J11J21
-J21J22-J11J12J11J22+J12J21·
2ξ2-2xξ2x-2yξ2y
2η2-2xη2x-2yη2y
2ηξ-2xηξx-2yηξy(10)1.3形函数
与传统等参单元类似,本文将在参考坐标系下构造单元的形函数,这样形函数的参考域与几何定义的参考域相同,最后在计算过程中通过参数变换可以得到物理域上的形函数。如图2所示,单元在4个顶点各配置4个自由度,分别为w, wξ, wη, wξη, 而在各边界内部每个节点配置两个自由度w, wn, 即挠度和法向转角, 各边上的节点数目分别为M, N, P, Q。根据混合函数插值,那么可以得到每个自由度對应的形函数,如顶点1SV1w=η+2η-124H(1)1ξ+
ξ+2ξ-124H(1)1η-
η+2η-12ξ+2ξ-1216
SV1wξ=η+2η-124H(1)0ξ+
ξ+1ξ-124H(4)1η-
η+2η-12ξ+1ξ-1216
SV1wη=η+1η-124H(1)1ξ+
ξ+2ξ-124H(4)0η-
η+1η-12ξ+2ξ-1216
SV1wξη=η+1η-124H(1)0ξ+
ξ+1ξ-124H(4)0η-
η+1η-12ξ+1ξ-1216(11)其中上标V1代表顶点1,类似地可以得到其他顶点处的形函数,不再赘述。同理,也可以得到各边界内部节点对应的形函数,如边界1上
S(1)w,i=η+2η-124H(1)iξ,i=2~M-1
S(1)wn,i=η+1η-124H(1)iξ,i=2~M-1(12)
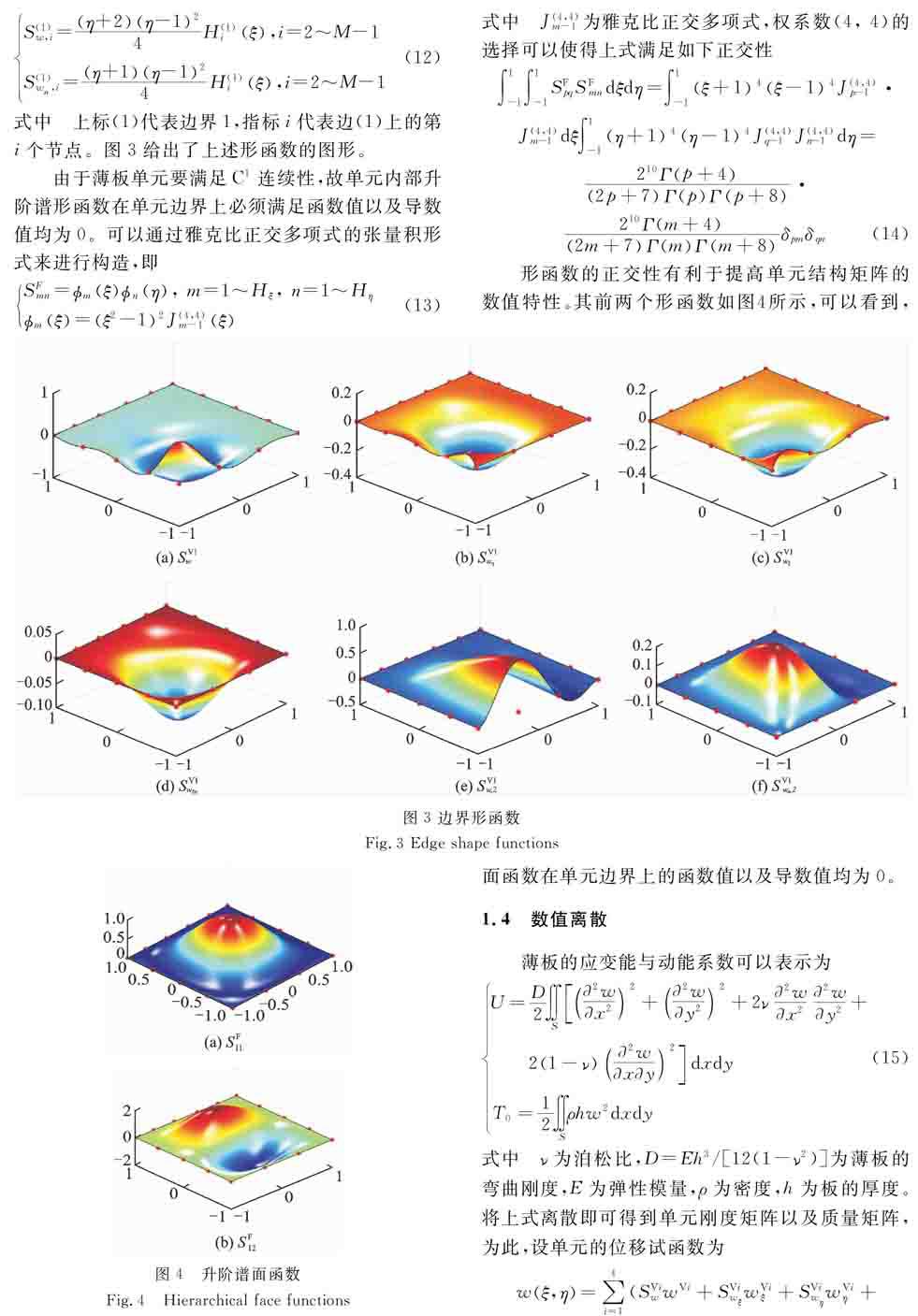
式中上标(1)代表边界1,指标i代表边(1)上的第i个节点。图3给出了上述形函数的图形。
由于薄板单元要满足C1连续性,故单元内部升阶谱形函数在单元边界上必须满足函数值以及导数值均为0。可以通过雅克比正交多项式的张量积形式来进行构造,即
SFmn=mξnη, m=1~Hξ, n=1~Hη
mξ=ξ2-12J(4,4)m-1ξ(13)
式中J(4,4)m-1为雅克比正交多项式,权系数(4, 4)的选择可以使得上式满足如下正交性∫1-1∫1-1SFpqSFmndξdη=∫1-1ξ+14ξ-14J(4,4)p-1·
J(4,4)m-1dξ∫1-1η+14η-14J(4,4)q-1J(4,4)n-1dη=
210Γp+42p+7ΓpΓp+8·
210Γm+42m+7ΓmΓm+8δpmδqn(14)形函数的正交性有利于提高单元结构矩阵的数值特性。其前两个形函数如图4所示, 可以看到,
图3 边界形函数
Fig.3 Edge shape functions图4升阶谱面函数
Fig.4Hierarchical face functions面函数在单元边界上的函数值以及导数值均为0。
1.4数值离散
薄板的应变能与动能系数可以表示为U=D2S2wx22+2wy22+2ν2wx22wy2+
21-ν2wxy2dxdy
T0=12Sρhw2dxdy(15)式中ν为泊松比,D=Eh3/[12(1-ν2)]为薄板的弯曲刚度,E为弹性模量,ρ为密度,h为板的厚度。将上式离散即可得到单元刚度矩阵以及质量矩阵,为此,设单元的位移试函数为wξ,η=∑4i=1(SViwwVi+SViwξwViξ+SViwηwViη+
SViwξηwViξη)+∑Hξm=1∑Hηn=1amnSFmn+
∑M-1i=2S(1)w,iw(1)i+S(1)wn,iw(1)n,i+
∑N-1i=2S(2)w,iw(2)i+S(2)wn,iw(2)n,i+
∑P-1i=2S(3)w,iw(3)i+S(3)wn,iw(3)n,i+
∑Q-1i=2S(4)w,iw(4)i+S(4)wn,iw(4)n,i(16)式中wVi,…,wViξη為顶点处的节点位移;w(j)i,w(j)n,j=1~4为边内的节点位移;amn为对应升阶谱面函数的广义节点位移。定义如下节点位移向量= [wV1,w(1)i(i=2~M-1),
wV2,w(2)i(i=2~N-1),
wV3,w(3)i(i=P-1~2),
wV4,w(4)i(i=Q-1~2),
wV1η,w(1)n,i(i=2~M-1),
wV2η,wV2ξ,w(2)n,i(i=2~N-1),
wV3ξ,wV3η,w(3)n,i(i=P-1~2),
wV4η,wV4ξ,w(4)n,i(i=Q-1~2),
wViξη(i=1~4),a11,a21,…,aHξHη]T通过高斯-洛巴托积分,详见文献[11],式(15)可以离散为如下形式U=12THTBH
T0=12ρhTGTCG(17)其中B=DCυC0
υCC0
0021-υC
H=Gxx
Gyy
Gxy(18)
C=diagC1,C2,…,CNξ,
Ci=CξidiagJi1Cη1,Ji2Cη2,…,JiNηCηNη,
Jij=detJ(ξi,ηj)(19)式中Cξi, Cηj为沿着ξ,η方向的高斯-洛巴托积分系数;Gxx, Gyy, Gxy为微分矩阵。注意到是参考系下的节点位移向量,因而不能直接用于单元组装与边界条件的施加,为此需要将其转化为x-y坐标系中的节点位移,如图2(右)所示,为此定义如下节点位移向量= [wV1,w(1)i(i=2~M-1),
wV2,w(2)i(i=2~N-1),
wV3,w(3)i(i=P-1~2),wV4,
w(4)i(i=Q-1~2),wn,1,…,
wn,M+P+Q+N,wxy,i(i=1~4),
a11,a21,…,aHξHη]T(20)同时可以得到可逆转换关系=Q(21)将上式代入式(17)可以得到U=12TQ-THTBHQ-1
T0=12ρhTQ-TGTCGQ-1(22)进而可以得到刚度矩阵与质量矩阵K=Q-THTBHQ-1
M=ρhQ-TGTCGQ-1(23)2算例
本节将上述单元用于求解薄板的自由振动问题,如图5所示为一扇形板,其圆弧边界的半径分别为a和b, 周向旋转角度为φ。本例中考虑两种边界条件,分别为四边简支(SSSS) 和两径向边简支,两周向边固支(SCSC)。表1研究了四边简支边界条件下扇形板的前6阶固有频率收敛过程,整个板采用一个单元计算(如图5所示),节点数目在各边界上相同,记为Ne, 而内部两个方向上的升阶谱形函数的数目也取为相同值Nh。计算过程中总自由度数记为TDOFs, 而施加边界条件之后的自由度数记为RDOFs。从表中可以看到,随着边界节点数目的增加,只需要少量的内部自由度即可达到收敛的计算结果(在表中考虑的有效数字范围内)。当边界节点数目为7,内部升阶谱面函数数目为7×7时,本文计算结果在考虑的有效数值范围内即可收敛于精确解,所需要的自由度数目为105,相比于其他数值方法,如微分求积有限元方法(DQFEM)、微分求积方法(DQM),所需自由度数更少。同样地,对于SCSC边界条件下的计算结果也有类似结论,如表2所示。
图5扇形板
Fig.5A sectorial plate
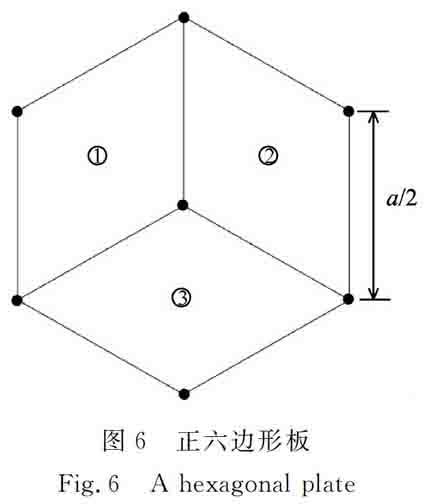
为验证单元组装时计算特性,考虑图6所示的正六边形板,边长为a/2, 整个板被划分为3个四边形单元,各单元边界上的节点数目与内部升阶谱面函数关系为Ne=Nh+2。表3中给出了六边简支和六边固支时的前6阶固有频率的计算结果和Liew用瑞利-里兹法以及Irie的解析方法结果。对于六边简支情况,由于角点存在弯矩奇异性,因此计算结果收敛速度较慢,而对于大多数频率参数,计算精度仍然能达到前3~5位有效数字收敛,且计算结果与其他方法相比吻合较好。对于固支边界情况,速度更快,能达到前6位有效数字收敛,且计算结果均比其他方法给出的频率要低。
图6正六边形板
Fig.6A hexagonal plate表1四边简支扇形板的前6阶固有频率收敛过程
Tab.1Convergence of the first 6 natural frequencies of SSSS sectorial plates
a/b=2.0, φ=45°,Ω=ωa2ρh/D
MethodNeNhRDOFs/
TDOFsMode sequence123456Present3757/7368.382152.34190.79282.49286.54390.18872/8868.382152.34190.79282.49286.53390.1720408/42468.382152.34190.79282.49286.53390.174876/9668.380150.99189.61282.42283.76390.17993/11368.380150.99189.61282.41283.76390.1720412/43268.380150.99189.61282.41283.76390.17510116/14068.379150.99189.60278.46283.61387.6611137/16168.379150.99189.60278.46283.61387.6520416/44068.379150.99189.60278.46283.61387.656884/11268.379150.98189.60278.45283.59387.669101/12968.379150.98189.60278.45283.59387.6520420/44868.379150.98189.60278.45283.59387.657660/9268.379150.98189.60278.43283.59387.70773/10568.379150.98189.60278.39283.59387.6220424/45668.379150.98189.60278.39283.59387.62Exact[13]68.379150.98189.60278.39283.59387.62DQFEM[14]N=12—/14468.379150.98189.60278.39——DQM[15]N=21—/44168.380150.96189.60278.35283.54387.62
表2SCSC扇形板的前6阶固有频率收敛过程
Tab.2Convergence of the first 6 natural frequencies of SCSC sectorial plates
a/b=2.0, φ=45°,Ω=ωa2ρh/D
MethodNeNhRDOFs/
TDOFsMode123456Present4985/113107.57178.84269.55306.05346.63477.2610104/132107.57178.84269.55306.05346.63477.2520404/432107.57178.84269.55306.05346.63477.25MethodNeNhRDOFs/
TDOFsMode123456Present5987/121107.57178.83269.54305.86346.56476.3110106/140107.57178.83269.54305.86346.56476.3020406/440107.57178.83269.54305.86346.56476.306989/129107.57178.82269.49305.84346.48476.3110108/148107.57178.82269.49305.84346.48476.3020408/448107.57178.82269.49305.84346.48476.307991/137107.57178.82269.49305.84346.46476.3110110/156107.57178.82269.49305.84346.46476.3020410/456107.57178.82269.49305.84346.46476.30Exact[13]107.57178.82269.49305.84346.46476.30DQFEM[14]N=11-/121107.57178.82269.49305.84——DQM[15]N=21-/441107.57178.79269.50305.80346.40476.24
表3正六邊形板的前6阶固有频率收敛过程
Tab.3Convergence of the first 6 natural frequencies of hexagonal plates
Ω=ωa/π2ρh/D
MethodNe = Nh + 2Mode sequence123456SSSSSSPresent52.9515.7.42297.426313.230813.236015.070772.93167.38887.390513.196113.199115.172892.92117.37407.375013.180813.182615.1970112.91507.36617.366813.172413.173515.2026132.91127.36147.361913.167213.168015.2033152.90867.35847.358813.163813.164415.2027172.90697.35637.356613.161413.161915.2017192.90567.35487.355113.159713.160115.2008212.90467.35377.353913.158513.158715.2001232.90397.35297.353113.157513.157715.1994252.90337.35237.352413.156713.156915.1988272.90297.35177.351913.156113.156315.1983Liew[16]2.92747.39927.415013.213513.240315.2745Irie[17]2.9107.3607.38213.18013.20015.240CCCCCCPresent55.148610.747910.751117.550017.562219.706875.171510.748310.748517.539817.540019.900095.178610.748310.748317.541417.541619.9644115.181210.748310.748317.542117.542219.9879135.182410.748310.748317.542417.542519.9981155.183010.748310.748317.542617.542620.0030175.183310.748310.748317.542717.542720.0057195.183510.748310.748317.542717.542720.0072215.183610.748310.748317.542717.542820.0081235.183610.748310.748317.542817.542820.0087255.183710.748310.748317.542817.542820.0091275.183810.748310.748317.542817.542820.0094Liew[16]5.288610.852510.856717.752817.781620.2331Irie[17]5.21210.85010.88017.73017.75020.130
3结论
本文提出了一种微分求积升阶谱薄板单元,单元形函数边界上采用插值型高阶Hermite多项式构造,其中高斯-雅克比点作为边界插值节点有效地提高单元的数值特性,而内部升阶谱面函数采用雅克比正交多项式的张量积来构造。该单元在边界以及内部节点配置自由,单元自由度的配置不随着网格传播,可以适用于局部自由度的调整以及连接不同阶次的单元。将本文计算结果与其他数值方法以及解析方法的结果对比表明,该单元不仅计算精度较高,收敛速度快,而且具有良好的数值稳定性。
参考文献:
[1]Courant R. Variational methods for the solution of problems of equilibrium and vibrations [J]. Bulletin of the American Mathematical Society,1943, 49(1): 1—23.
[2]Turner M J. Stiffness and deflection analysis of complex structures[J]. Journal of the Aeronautical Sciences, 1956, 23(9): 805—823.
[3]Zienkiewicz O C, Taylor R L, Taylor R L, et al. Finite Element Method: Its Basis and Fundamentals[M]. Beijing: Beijing World Publishing Corpoaratoin, 2013.
[4]Babuska I, Szabo B A, Katz I N. The p-version of the finite element method[J]. Siam Journal on Numerical Analysis 1981, 18(3): 515—545.
[5]Babuka I, Suri M.The p- and h-p versions of the finite element method, an overview[J]. Computer Methods in Applied Mechanics and Engineering, 1990, 80(1990): 5—26.
[6]Zienkiewicz O C, De S R Gago J P, Kelly D W. The hierarchical concept in finite element analysis[J]. Computers & Structures 1983, 16(1): 53—65.
[7]Peano A. Hierarchies of conforming finite elements for plane elasticity and plate bending[J]. Computers & Mathematics with Applications, 1976, 2(3): 211—224.
[8]Bardell N S. The application of symbolic computing to the hierarchical finite element method[J]. International Journal for Numerical Methods in Engineering, 1989, 28(5): 1181—1204.
[9]Bardell N S. Free vibration analysis of a flat plate using the hierarchical finite element method[J]. Journal of Sound & Vibration, 1991, 151(2): 263—289.
[10]諸德超.升阶谱有限元法[M]. 北京:国防工业出版社, 1993.
[11]Liu C, Liu B, Zhao L, et al. A differential quadrature hierarchical finite element method and its applications to vibration and bending of Mindlin plates with curvilinear domains[J]. International Journal for Numerical Methods in Engineering , 2016, 109(2): 174—197.
[12]Shen J, Tang T, Wang L L. Spectral Methods: Algorithms, Analysis and Applications[M]. Berlin: Springer, 2011.
[13]Kim C S, Dickinson S M. On the free, transverse vibration of annular and circular, thin, sectorial plates subject to certain complicating effects[J]. Journal of Sound and Vibration,1989, 134 (3):407—421.
[14]Xing Y, Liu B. High-accuracy differential quadrature finite element method and its application to free vibrations of thin plate with curvilinear domain[J]. International Journal for Numerical Methods in Engineering, 2009, 80 (13):1718—1742.
[15]Bert C W, Malik M.The differential quadrature method for irregular domains and application to plate vibration[J]. International Journal of Mechanical Sciences,1996, 38 (6):589—606.
[16]Liew K M, Lam K Y A. Set of orthogonal plate functions for flexural vibration of regular polygonal plates[J]. Journal of Vibration and Acoustics,1991, 113 (2):182—186.
[17]Irie T, Yamada G, Umesato K. Free vibration of regular polygonal plates with simply supported edges[J]. The Journal of the Acoustical Society of America, 1981, 69 (5):1330—1336.
A differential quadrature hierarchical finite element method and its
application to thin plate free vibrationWU Yang, XING Yu-feng(Institute of Solid Mechanics, Beihang University (BUAA), Beijing 100191, China)
Abstract: A Hermite differential quadrature hierarchical finite element method is proposed and elaborated in this paper. The geometric mapping is based on blending function interpolation, while the shape functions at the element edges are derived from Hermite interpolation bases with non-uniform distributed nodes and the internal hierarchical face functions are obtained through tensor product of one dimensional Jacobi orthogonal polynomials. The shape functions in conjunction with Gauss-Lobatto interpolation are employed in discretizing the potential functional of thin plates to obtain the element matrices. In the present elements, the DOFs (Degree of Freedoms) collocations are free at each side and inside of the element, therefore it is allowed to use elements with different order in assembly. The present elements are used in free vibration analysis of thin plate, and the results are compared with the exact solutions and the numerical results by other methods, which show the high accuracy as well as fast convergence of present elements. Moreover, the stability problems are not suffered even when the element order is very high.
Key words: vibration of thin plates; differential quadrature method; Hermite interpolation; hierarchical finite element method

