架空线路无覆冰导线舞动的参数共振机理
刘亮 郝震 崔赟 邢誉峰 蔡巍 邓春
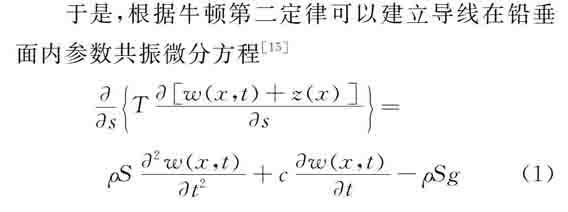


摘要: 为了解释架空线路导线舞动现象的成因,通过将风载荷等效为轴向周期位移激励的方法,对架空线路单导线舞动进行了研究,认为无覆冰单导线的舞动就是参数共振。引起导线舞动的主要因素是线路系统自身参数的周期性变化,当轴向位移激励频率和导线系统频率满足一定关系时,导线系统将发生大幅度横向参数共振即舞动。模拟运行线路舞动试验验证了用参数共振理论能够解释无覆冰架空单导线系统的起舞现象。
关键词: 风致振动; 单导线; 舞动; 参数共振; 振动试验
中图分类号:TM752+.5; TM726.3文献标志码: A文章编号: 1004-4523(2018)02-0308-06
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.014
引言
作为一种低频、大振幅的风致振动,架空线路导线舞动问题相当复杂,已经困扰工程界很长时间[1-2]。从20世纪30年代起,包括美国、加拿大、英国、日本以及中国等舞动事故高发的国家相继投入大量的努力对导线舞动机理以及有效的防舞措施展开了研究[3-6]。已有研究成果给出了3种主要舞动成因,包括非对称导线覆冰、横向风载荷激励以及导线系统自身结构参数的影响[7]。
由于舞动事故多发于覆冰导线,目前的传统舞动机理包括Den Hartog提出的垂直舞动机理[8-9]以及O Nigol得到的扭转舞动机理[10]都把关注焦点放在了由于非对称覆冰引起的升力上。然而,在实际运行线路中,当导线在薄覆冰(覆冰厚度不足以形成非对称截面)及无覆冰情况下时,也陆续观测到若干起舞动破坏的事故[11-12]。由于这些现象无法通过传统机理来解释,有必要提出一种能够解释薄(无)覆冰情况下的舞动机理。蔡廷湘[12]认为舞动的机理是激励频率与导线固有频率接近致使系统发生了共振。以此为切入点,谢文丽等[13]给出了导线起舞时受力与频率之间关系的一种理论计算方法。
本文则从参数共振角度来解释薄(无)覆冰情况下的舞动机理。首先建立了导线参数共振模型,然后用单档距试验结果验证了本文模型的合理性。
1导线参数共振模型
架空导线系统在风激励作用下,杆塔不可避免地会产生横向振动,即使杆塔是刚性的,风激励的作用也可以近似等效为杆塔的弹性振动。对导线而言杆塔振动构成导线的动态边界,在纵向相当于有一个位移激励。这为作者将风载荷等效为轴向位移激励提供了依据。
单跨导线振荡系统可以被视作是一个两端简支的柔索结构。在柔索结构一端施加轴向位移激励将会产生面内的参数共振,从而将无覆冰导线舞动问题转化成为由轴向位移激励引发的两端简支柔索结构的参数共振问题,如图1所示。
为了简化分析过程,利用如下4个假设[14-15]:
(1) 在静载情况下,导线的弧垂曲线视作抛物线;
(2) 忽略导线的弯曲、扭转以及剪切刚度;
(3) 不考虑导线张力沿导线轴向的变化;
(4) 导线在振动过程当中始终处于弹性状态。
于是,根据牛顿第二定律可以建立导线在铅垂面内参数共振微分方程[15]sTwx,t+zxs=
ρS2wx,tt2+cwx,tt-ρSg(1)式中T为导线切向张力,S为导线截面积,ρ为导线密度,w(x,t)为导线偏离静平衡位置的横向位移,z(x)为导线在重力作用下静平衡位置,c为单位长度的阻尼系数,s为导线的弧长坐标。
根据假设(3),将导线张力T及其轴向分力A(下面称为轴向张力)的微分关系T=Adsdx代入方程(1))进行化简得ρS2wx,tt2+cwx,tt-ρSg-A·
1+d2zdx2-122wx,tx2+d2zxdx2=0(2)图1受轴向位移激励导线的参数共振模型示意图
Fig.1Parametric oscillation model for conductor excited by an axial periodic displacement
根据假设(1),导线的重力垂度曲线可以表示为zx=ρSg8A0L2-4x2(3)第2期刘亮,等:架空线路无覆冰导线舞动的参数共振机理振 动 工 程 学 报第31卷式中A0=ρSgL28z0为最大垂度处的张力,L为导线长度(即档距长度),z0为导线中点处的垂度或最大垂度。导线在运动过程中,A包括静态张力A0以及动态张力Ad,而 Ad=Aωsinωt+AN(4)其中右端第一项是由导线右端位移激励引起的弹性动张力,AN为导线几何非线性引起的附加动张力Aω=ESL1Xd
AN=ESL112∫L2-L2wx2dx+8z0L2∫L2-L2wdx (5)参数L1=L1+8z0L2为考虑导线弧垂的导线长度,E为弹性模量,Xd和ω分别是位移激励的幅值和圆频率。
为了便于参数化分析,对公式(2)进行无量纲处理得22+2ξc1-1+ωsin+N·
1π222+ωsin+N8γπ2=0(6)式中各无量纲参数的定义如下:=xL, =wL, =ω0t,1=ω1ω0, =ωω0,
ω=AωA0, N=ANA0, d=XdL,
ω0=πLA0ρS, ω1=ω01+2/π4λ2212,
γ=z0L, k2=ESA0, λ2=64k2γ21+8γ2(7)式中ω0以及ω1分別为把导线视为张紧索和考虑垂度影响的柔索一阶圆频率,γ为导线的垂跨比,ξc为导线的阻尼比,λ为导线的Irvine参数。
下面采用Galerkin加权残量方法求解非线性方程(6)。把位移函数写成如下已知基函数的叠加形式x,t=∑∞j=1qjj(8)其中基函数为标准弦模态函数,即j=sinjπ+12, j=1,2,…(9)与各阶模态函数相应的固有频率为fj=j2LA0ρS(10)将公式(8)代入公式(6)中,利用Galerkin方法可以给出前两阶模态耦合的非线性动力学方程组1+2ξc11+Ω21q1=-3α1q21-4α1q22-
α2q31-4α2q1q22-32γπ3ωsin
2+2ξc12+Ω22q2=-8α1q1q2-
4α2q21q2-16α2q32 (11)式中Ω21=21+ωsin,α1=λ2/(8πγ),Ω22=41+ωsin,α2=π2λ2/(256γ2)
方程(11)为非线性参数共振方程,需要利用直接积分方法或非线性多尺度方法求解。本文利用MATLAB的龙格库塔方法对方程(11)进行了求解。
从方程(11)求得q1和q2后,根据公式(8)可得沿轴向任何一点处的振动幅wA=Lq1sinπ+12+
Lq2sin2π+12 (12)公式(10)给出了非线性导线系统对应的线性系统的各阶固有频率。对参数共振系统而言,发生特定阶次参数共振的激励频率区域被称为动力不稳定区域[16],动力不稳定区域是指激励频率与系统固有频率间满足f=2fjk, k=1,2,3,4,…(13)当激励频率f等于某阶固有频率的两倍,即在f=2fj附近时,最易于发生参数共振(系统将产生大幅度振动),这一区域被称作主要动力不稳定区域。
由此可見,导线舞振可以看作是激励频率位于导线系统的各阶动力不稳定区域内时系统做的大幅度参数共振。为了验证该结论,将实验结果与理论结果进行了对比分析。
2导线参数共振试验
导线系统的参数舞振实验是在冀北电力公司带电作业培训中心进行的。
北侧悬挂点位于备品库屋顶立起一根槽钢上,槽钢顶部经钢拉线与房顶圈梁固定;南侧悬挂点位于大门处的一根钢柱上,钢柱地脚采用膨胀螺栓与水泥地面连接,钢柱上端部采用4根钢拉线固定防止摆动,另外沿导线方向增加一根钢拉线用来抵消试验导线悬挂拉力,如图2所示。
图2试验台两侧悬挂点
Fig.2Suspension points of both sides of experiment rig
图3为导线平台的结构示意图,试验导线在南侧悬挂点经过一个定滑轮与卷扬机连接用以调整悬挂导线的张紧程度;在北侧悬挂点则通过一个滑轮组与驱动装置连接。试验驱动装置为一台GS 225M-4三相异步电动机,通过1000∶1的变频器改变转数后获得0.5 Hz的额定转数,用以模拟实际运行线路中受到的风激励频率。在变频器的输出轴上安装飞轮稳定转速,飞轮上安装偏心杆,如图4所示。从该处连接细钢丝绳,钢丝绳通过滑轮组与导线连接,从而为试验导线施加了轴向周期位移激励。
试验时电动机由变频电源供电,改变变频电源输出的频率就可以改变电动机转速从而改变导线端部轴向激励的频率;与此同时,改变偏心杆的位置就可以改变轴向激励的幅值。在钢丝绳上串接拉力传感器以测量钢丝绳中的张力。图3试验导线振荡平台结构示意图
Fig.3Schematic illustration of test conductor oscillation experiment rig
图4试验驱动装置(飞轮及偏心杆)
Fig.4System of experimental driving device(flywheel and eccentric rod)
试验时测量的参数主要包括参数共振频率、振幅、张力和导线振荡形态。频率和张力由张力计数据得到,振幅仅在两个特征位置(试验导线1/2及3/4位置)处利用标尺测量。导线振荡形态则是通过试验人员分段观测档距内振荡波数获得的。
3结果与讨论
在实际的运行线路中,导线截面尺寸一般为几百平方毫米,理想情况下,试验用导线应该尽可能与实际运行线路保持一致。但试验导线如果也采用实际线路常用的几百平方毫米的导线,将要求驱动导线舞动的试验功率极大,这会导致试验平台驱动装置难以购置,试验平台难以建设。因此,本文采用较细的钢芯铝绞线LGJ16/3作为试验导线,分别在285 m以及800 m这两种基本能够覆盖实际运行单档距线路的特征档距情况下进行试验。悬挂试验导线时调整静态轴向应力与真实线路运行的导线尽可能一致,但导线所承受的拉力却会远小于实际线路情况。
为了避免材料和几何参数误差,试验前对导线杨氏模量、截面积以及密度均进行了测量,图5是通过单轴拉伸试验结果得到的导线应力-应变曲线,测得杨氏模量为62 GPa;使用游标卡尺测得导线外径为4.9 mm,即截面积为18.82 mm2;取一截导线测得其密度为3464.4 kg/m3。
图5试验用LGJ16/3导线拟合应力-应变曲线
Fig.5Fitting stress-strain curve of LGJ16/3 conductor used in the experiment
实验时,285 m和800 m档距导线静态轴向拉力分别为735 N和2685 N,飞轮偏心距分别取6 cm与8 cm。根据公式(10),可以分别得到两种档距情况下导线系统的前两阶固有频率如表1所示。对应地,根据公式(13),表2给出了导线系统在两种档距情况下前两阶动力不稳定区域的范围。
表1不同档距下系统前两阶固有频率
Tab.1System eigenfrequencies of the first two orders under different spans
档距/m静态轴向拉力/N1阶频率/Hz2阶频率/Hz2857350.18630.372580026850.12680.2537
表2不同档距下系统前两阶动力不稳定区域
Tab.2System dynamic instability regions of the first two orders under different spans
档距/m静态轴向
拉力/Nk1阶动力
不稳定区域
频率/Hz2阶动力
不稳定区域
频率/Hz2857351
20.3725
0.18630.7450
0.372580026851
20.2537
0.12680.5074
0.2537
由表2可知,285 m档距系统的第1阶主要动力不稳定区域(对应固有频率f1)在2f1=0.3725 Hz附近,而第2阶主要动力不稳定区域(对应固有频率f2)在2f2=0.745 Hz附近;而800 m档距系统的第1阶主要动力不稳定区域在2f1=0.2537 Hz附近,第2阶主要动力不稳定区域在2f2=0.5074 Hz附近。在两组不同档距试验中,分别选取4个频率点
进行观测,试验结果见表3和4。
从结果可以看出,285 m档距下随着激励频率远离第1阶主要动力不稳定区域并靠近第2阶主要动力不稳定区域,中点位置振幅逐渐减小而3L/4位置处的振幅逐渐增大,振型也逐渐由1阶形态转变为2阶;而800 m档距下,两个特征点的振幅相比于285 m档距都很小,同时观测到的振型也基本都是10阶以上的杂乱高阶振型,可以认为在800 m情况下导线系统并没有发生参数舞振,出现的杂乱高阶振型是由于端部轴向位移激励带来的行波。
表3285 m档距下特征点振幅及系统振型试验结果
Tab.3Experiment results of amplitudes of typical points and oscillation modes (285 m span)
激励
频率/HzL/2位置
振幅/m3L/4位置
振幅/m观测
振型0.5301.150.251阶0.5700.950.401阶0.6650.350.852阶0.7550.251.252阶
表4800 m档距下特征点振幅及系统振型试验结果
Tab.4Experiment results of amplitudes of typical points and oscillation modes (800 m span)
激励
频率/HzL/2位置
振幅/m3L/4位置
振幅/m观测
振型0.300.050.1310阶0.350.200.1512阶0.450.100.0414阶0.500.400.0516阶
下面针对发生舞动的285 m档距系统,通过经典龙格库塔方法对公式(11)中的耦合非线性常微分方程进行了求解,其中阻尼比取ξc为0.05,初始条件为q10=q20=3.51×10-7即初始扰动为0.0001 m。图6(a)和(b)分别对比了数值计算得到的两个特征点处振幅随激励频率变化的关系,可以看出结果的趋势吻合得很好,这也就验证了用参数共振机理能够解释导线振荡平台的试验现象。
图7给出了激励频率为0.52 Hz时导线中点偏离平衡位置橫向位移时程曲线;针对激励频率0.52和0.76 Hz, 图8给出了导线偏离平衡位置最大位移处的形貌曲线,这与实验观测到的舞振形态是吻合的。图6285 m档距下特征点振幅试验/理论预测对比
Fig.6The comparison between the oscillation amplitude of analytical prediction and experiment results
图7激励频率为0.52 Hz时导线中点偏离平衡位置横向位移时程曲线
Fig.7Time history curve of midpoint transverse displacement deviation from equilibrium position with 0.52 Hz excitation frequency图8导线偏离平衡位置最大位移处的形貌曲线
Fig.8The profile of the maximum displacement at the equilibrium position of the conductor4结论
1) 无覆冰导线舞动现象的产生主要依赖于导线系统自身的结构参数,对特定导线而言,档距和静态轴向拉力是决定舞振频率的主要因素。
2) 随着等效轴向位移激励频率接近某阶主要动力不稳定区域,系统将发生该阶参数共振;当激励频率介于两阶主要动力不稳定区域之间时,系统振型将逐渐发生转变。
3) 相比于小档距线路,大档距线路产生舞动需要输入的外界能量要求更高。
4) 可以通过设计线路导线的静态轴向拉力来控制系统的主要动力不稳定区域以避开常见外载荷的激励频率实现防舞。
为了进一步验证本文提出的导线舞动参数共振机理,有必要采集实际运行线路的舞动数据加以分析。参考文献:
[1]LILIEN J L. Review of galloping control methods[J]. Electra, 2000, 191:45—61.
[2]WANG J. Overhead transmission line vibration and galloping[C].Proceedings of the International Conference on High Voltage Engineering and Application, Chongqing, China: IEEE Xplore, 2008:120—123.
[3]郭应龙,恽俐丽,鲍务均,等. 输电导线舞动研究[J].武汉水利电力大学学报, 1995, 5:506—509.
Guo Yinglong, Yun Lili, Bao Wujun, et al. A study on the galloping of overhead transmission line[J]. Journal of Wuhan University of Hydraulic & Electric Engineering, 1995, 5:506—509.
[4]朱宽军,刘彬,刘超群,等. 特高压输电线路防舞动研究[J]. 高电压技术, 2007, 33(11):12—20.
Zhu Kuanjun, Liu Bin, Liu Chaoqun, et al. Research on anti-galloping of UHV transmission line[J]. High Voltage Engineering, 2007, 28(34):12—20.
[5]向玲,任永辉,卢明,等. 特高压输电线路防舞装置的应用仿真[J]. 高电压技术, 2016, 42(12):3830-3836.
Xiang Ling, Ren Yonghui, Lu Ming. Simulation of anti-galloping device′s application in UHV transmission line[J]. High Voltage Engineering, 2016,42(12):3830—3836.
[6]姜雄, 楼文娟. 三自由度体系覆冰导线舞动激发机理分析的矩阵摄动法[J]. 振动工程学报, 2016, 29(6):1070—1078.
Jiang Xiong, Lou Wenjuan. Matrix perturbation method for analysis of 3 DOF iced transmission line galloping mechanism[J]. Journal of Vibration Engineering, 2016, 29(6):1070—1078.
[7]王少华,蒋兴良,孙才新.输电线路导线舞动的国内外研究现状[J]. 高电压技术, 2005, 31(10):11—14.
Wang Shaohua, Jiang Xingliang, Sun Caixin. Study status of conductor galloping on transmission line[J]. High Voltage Engineering, 2005, 31(10):11—14.
[8]Denhartog J P. Transmission line vibration due to sleet[J]. Electrical Engineering, 2013, 51(6):413.
[9]Nigol O, Buchan P G. Conductor galloping Part I - Den Hartog Mechanism[J]. IEEE Transactions on Power Apparatus & Systems, 1981, PAS-100(2):699—707.
[10]Nigol O, Buchan P G. Conductor galloping-Part II Torsional Mechanism[J]. IEEE Transactions on Power Apparatus & Systems, 1981, PAS-100(2):708—720.
[11]Davis D A, Richards D J W, Scriven R A. Investigation of conductor oscillation on the 275 kV crossing over the rivers Severn and Wye[J]. Proceedings of the Institution of Electrical Engineers, 1963, 110(1):205—219.
[12]蔡廷湘.輸电线舞动新机理研究[J]. 中国电力, 1998, 10:62—66.
Cai Tingxiang. A New Mechanism of transmission line galloping[J]. Electric Power, 1998,10: 62—66.
[13]谢文丽,王茂成,王冠宇,等. 架空输电导线机械起舞受力与频率关系的理论计算[J]. 电力科学与工程, 2016, 32(9):40—47.
Xie Wenli, Wang Maocheng, Wang Guanyu, et al. Theoretical calculation on relationship between force and frequency of overhead transmission conductor mechanical galloping[J]. Electric Power Science & Engineering, 2016, 32(9):40—47.
[14]亢战, 钟万勰. 斜拉桥参数共振问题的数 值研究[J]. 土木工程学报,1998, 4:14—22.
Kang Zhan, Zhong Wanxie. Numerical study on parametric resonance of cable in cable stayed bridge[J]. China Civil Engineering Journal, 1998, 4:14—22.
[15]李鳳臣.大跨度桥梁斜拉索的参数振动及索力识别研究[D].哈尔滨:哈尔滨工业大学, 2010.
Li Fengchen. Parametric vibration and cable force identification of staying cable of large-span bridges[D]. Harbin: Harbin Institute of Technology, 2010.
[16]邢誉峰,李敏.工程振动基础[M].第2 版.北京: 北京航空航天大学出版社,2011.
Xing Yufeng, Li Min. Engineering Vibration Foundation[M]. 2nd ed. Beijing: Beihang University Press, 2011.
Parametric resonance mechanism of conductor galloping
without icing on overhead lineLIU Liang1, HAO Zhen1 , CUI Yun2 , XING Yu-feng2 , CAI Wei1, DENG Chun1
(1. Electric Power Research Institute of State Grid JIBEI Electric Power Company, Beijing 100045, China;
2. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China)
Abstract: In order to explain the causes of the overhead line conductor galloping phenomenon better, the galloping on overhead line with a single conductor is studied by equating the wind load to axial periodic displacement excitation. It is concluded that the galloping of a single conductor without icing is parametric resonance. According to this mechanism, the main influence factors of the galloping are the periodic variation of transmission line system′s parameters. The parametric resonance of system will occur, i.e. galloping, when the excitation frequency and eigenfrequency of system satisfy a certain relationship. The mechanism established is verified to be able to explain the transmission line conductor galloping through simulated operational line vibration experiments.
Key words: wind-induced vibration; single conductor; galloping; parametric resonance; vibration experiment

