基于改进模糊物元分析法的辽宁省最严格水资源管理评价

陆静良

(辽宁省铁岭水文局，辽宁 铁岭 112000)

回良玉曾在2009年的全国水利工作会议上提出，应结合我国的水利基本国情建立最严格水资源管理制度，严格按照“三条红线”进行水资源管理；陈雷部长在全国水资源管理会议上提出实现社会经济的可持续发展必须保证实施水资源的最严格管理[1]。我国政府提出当前水资源过度开发问题应严格控制、明显改善水资源浪费和严重污染问题，努力按照“三条红线”基本要求保证用水总量、用水效率系数和纳污能力符合控制标准。根据中央、国务院提出的基本要求和根本出发点，我国水利学者利用多种手段和技术方法从多方面开展了大量的研究，其中主要包含“三条红线”的解析、基本思路和主要原则、实施措施和制度保障等，而有关水资源管理水平和主要问题的研究相对较少[2]。随着水资源管理的进一步发展和研究，全国范围内普遍建立了关于水资源管理的制度和相关措施。目前，对水资源管理水平进行评价，以及全面、科学地对未来水资源管理状况进行预测已成为验证水资源管理相关制度措施是否科学合理的主要研究内容。科学合理地对评价指标进行筛选将直接影响评价结果的准确性和科学性，故对不同的研究区域应结合当地的水资源管理实际情况建立评价指标体系。用于水资源评价的方法很多，主要有层次分析法、熵权法、模糊分析法以及组合权重法等，因此，应结合区域经济发展状况和水资源开发利用情况，采取科学合理的计算评价方法对水资源管理水平的评价具有重要意义[3- 6]。

据此，文章在详细分析了物元分析的基本理论和计算方法的基础上，分别利用层次分析法和熵权法对体系中指标层和准则层的指标权重系数进行计算，然后建立了基于改进模糊物元分析法的最严格水资源评价模型，对辽宁省水最严格资源管理水平进行模拟和预测。

1 基于改进的熵权模糊元分析法

1.1 基于改进熵权法的权重计算

目前层次分析法、变权分析法、熵值法和博弈组合权重法等是应用于最严格水资源管理评价的主要评价方法。其中层次分析法是以专家学者的知识经验对指标权重进行赋值，该方法具有一定直观判断性，受个人影响因素较大；变权分析法主要是适用于在指标赋予值过低时可对整体评分产生显著影响的情况，该方法是通过提高过低分数指标的权重使综合评价得分更加合理；熵值法是对指标离散程度赋予客观的指数，但可能会远远偏离指标在实际情况中的权重比值；博弈组合权重法是将不同评价指标权重进行关联、法则规划等作用，以权重集的形式进行赋权，具有一定的可靠性[7]。

因对研究区域生态效应成效机制的认识存在一定的局限性和缺陷，且为了提高评价结果的可信度，使其更加贴近实际情况，文章在充分考虑了各种主客观因素的基础上，采用组合赋权的方法对评价指标进行权重计算[8]。文章所采用的层次分析法主要是以专家的知识经验为基础，首先将关键因素按照一定的规则自上而下地分解成若干层，然后按照指标尺度构造各层要素之间的判断矩阵，并通过检验指标一致性结果计算权重向量，进行权重组合。文章分别利用熵权法和层次分析法对不同层级的评价指标进行权重系数计算，计算过程如下：

首先设定水资源管理评价的方案个数为n，评价体系中包含的指标数总数为m，表达为X=(xij)m×n;(i=1，2，…，m;j=1，2，…，n)。因不同评价指标之间的量纲和单位存在一定的差异性，故需对判断矩阵进行统一规范化处理，并得到相对隶属矩阵：R=(rij)m×n(i=1，2，…，m;n=1，2，…，n)。

经济型评价指标其计算结果越大则评价越优，经济型评价指标的相对隶属度可采用下式进行计算：

(1)

成本型评价指标其计算结果越小越优，此类评价指标的相对隶属度可采用下式进行计算：

(2)

式中，rij—第j个评价方案中的第i项评价指标的相对隶属度；(xij)max、(xij)min—在不同方案中同一评价指标xij的最大值和最小值。

评价指标熵的确定可按下式进行计算：

(3)

(4)

式中，Hi—方案中第i项评价指标的熵值；n—所选方案的总数；fij—第j个评价方案中的第i项指标权重占评价的权重值。

根据上述计算结果可对各评价指标的熵权进行计算，计算公式如下：

W=(ωi)1×m

(5)

(6)

式中，ωi—各评价指标的熵权，取值范围为0～1，所有评价指标的熵权之和为1；W—熵权特征向量。

将上述一级和二级权重计算结果进行综合计算可得AHP-熵权的合成权重即为评价指标目标层的组合权重，综合计算公式如下所示：

Wj=WiWij

(7)

式中，Wj—评价指标在目标层的组合权重；Wi—一级权重即准则层相对熵权；Wij—二级权重即指标层相对熵权。

1.2 构建模糊元模型

事物、特征和向量是描述物元分析理论的关键性参数要素，设定体系评价对象为M，其特征为C，特征向量为X，则进行评价的基本物元为R=(M，C，X)，利用上述的评价事物、特征和向量分析研究这些物元及其变化规律。设定向量X具有一定的模糊性即X为基本模糊物元，设定M具有m个评价指标C1，C2，…，Cm和向量值X1，X2，…，Xm。综上所述，R即为具有m个维度的模糊物元，则具有m个维度的n个样本构成的复合模糊物元如下所示：

(8)

式中，Xij—第i个评价指标在j样本中的模糊量值。

不同评价指标之间的单位和量纲存在一定的差异，故需对模糊物元进行从优隶属度计算，结合不同评价指标的类型，则经济型和成本型评价指标的从优隶属度可按下式进行计算：

(9)

式中，μij—方案j在第i项评价指标的从优隶属度；(Xij)max、(Xij)min—分别为评价指标的最大值和最小值。

根据上述计算结果可构建在n个样本中的m项评价指标从优隶属度模糊元矩阵如下：

(10)

文章中模糊物元R0m与Rmn之间的差的平方用Δij(i=1，2，…，m;j=1，2，…，n)表示，则模糊物元RΔ的表达式如下：

(11)

文章通过计算欧式贴近度ρHj，构建贴近度模糊物元矩阵RρH，计算公式如下：

(12)

RρH=[ρH1，ρH2，…，ρHn]

(13)

2 辽宁省最严格水资源管理评价指标体系

2.1 研究区域概况

辽宁省位于我国东北地区西南部，属于温带、寒温带大陆性季风气候，冬季寒冷干燥漫长，夏季多雨炎热，全年降雨量和径流量分布不均匀，其中西部水资源面积较大[9]。辽宁省工业发展充分、畜牧业和农林业发展迅速，不仅是我国的粮食基地也是工业发展中心。研究区域地势由东南向西北呈逐渐降低趋势，包含低山地丘陵区，在水资源管理中主要出现的问题有水供应能力不足，局部地下水过度开采、水污染和浪费情况严重、工农业废水排放不达标、水资源净化设施不完善等[10]。随着社会的发展以及人们对生活质量的提高，当前的水资源问题已无法保证人们正常生活水平质量的需要，严重制约了东北部地区的经济发展。为保障经济建设的健康发展，提高人们生活水平质量并缓解供水紧张压力，就必须建立健全水资源管理制度，加强水资源综合管理控制，节约减少水资源浪费，合理开发利用水资源[11]。

2.2 建立评价指标体系

全面、科学地对评价指标进行筛选是影响评价结构准确性的主要影响因素之一，文章结合辽宁省水资源分布结构和开采利用现状，通过将理论分析法和专家经验法相结合建立了水资源管理评价指标体系，并结合相关资料数据确定了各评价指标的标准等级，评价指标体系和标准见表1。

表1中性质栏，升代表越大越优型指标，降代表越小越优型指标，A1表示水资源人均用量、A2表示水资源开发利用率、A3表示农业用水比例、A4表示生态用水比例、B1表示GDP万元用水量、B2表示工业万元增加值用水量、B3表示农业灌溉利用系数、C1表示达标率、C2表示生活污水处理率、C3表示排放废水合格率，文章以2015年的水资源管理现状为基准，对2018年和2020年水平年的管理水平进行预测评价。

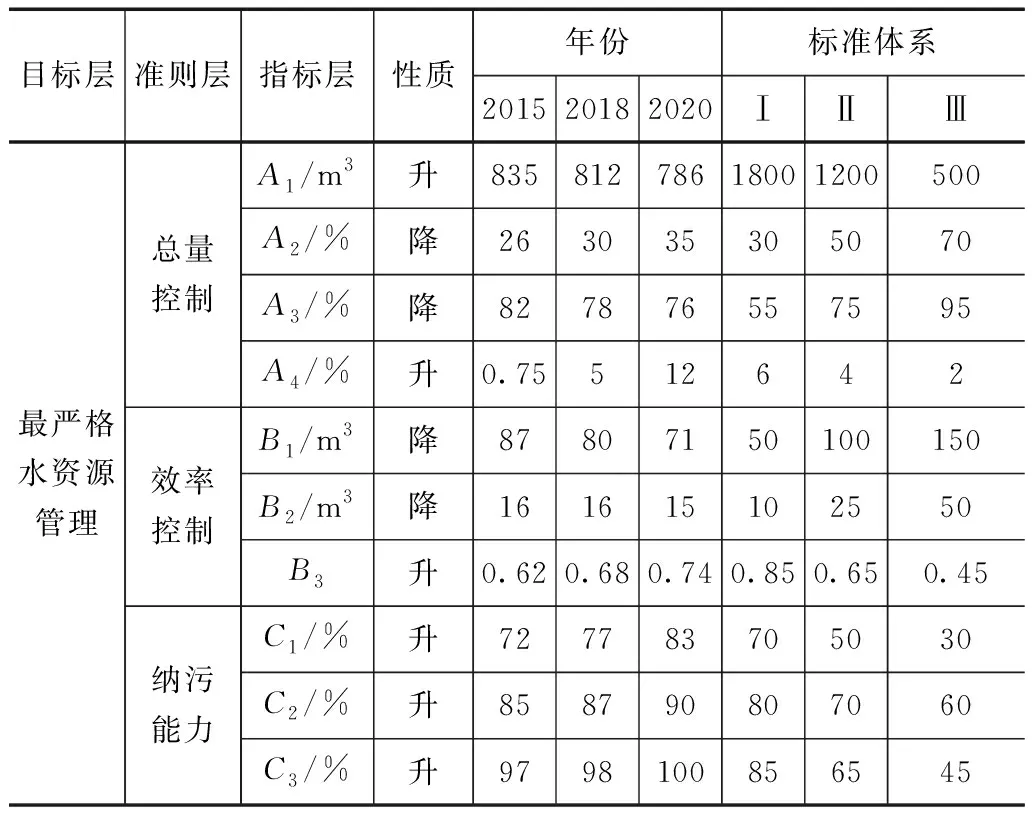
表1 辽宁省水资源评价指标体系及标准

3 辽宁省最严格水资源管理评价

3.1 基于改进熵权法的指标权重计算

首先构造判断矩阵，确定一级权重为然后确定指标层对准则层的权重。根据表1所构建的辽宁省最严格水资源管理评价指标体系及其评级标准，用熵权法公式计算出指标层对准则层的二级权重，以及指标层对目标层的组合权重，见表2。

表2 辽宁省水资源管理指标评价体系及指标权重系数

3.2 构建模糊物元分析模型

结合文中所述的熵权法计算基本公式和评价指标赋予系数，构建了评价模型，根据辽宁省的不同年份的样本和指标数据建立了模糊物元R，然后利用文中所述公式的从优隶属度构建了Rmn，并根据计算公式构造RΔ，计算结果分别如下：

欧式贴进度ρHj的计算是以各评价指标的权重计算结果为基准，利用模糊矩阵元RρH进行计算，各样本的贴进度计算结果如下：

3.3 评价结果分析

计算得到辽宁省2015年、2018年和2020年最严格水资源管理水平：2015年Ⅱ级,2018年Ⅱ级,2020年Ⅰ级。根据表1中对辽宁省2018年和2020年各评价指标的预测结果，采用改进的模糊物元分析法对各规划水平年辽宁省最严格水资源管理水平进行预测[12]。

文章在确定了各评价指标的权重系数后，将熵值法与赋权法进行组合赋权，然后通过查阅相关文献资料并借鉴有关专家学者的经验公式，对各评价指标的灵敏性进行分析和判断[13]，计算结果见表3。

表3 权重系数灵敏度计算结果

由表3可知，若要维持方案的优劣排序，各指标权重变化区间长度ω3>ω1>ω2，即用水效率控制的权重变化区间最小，敏感性最大；而纳污能力的敏感性变化区间最大，故其受其他因素的影响作用程度较小，这也与辽宁省的实际情况保持一致。综上所述，文章的权重系数整体敏感性较低，模型的评价结果具有良好的科学性和可靠度。

4 结语

文章在详细分析了熵权法和层次分析法的基本原理和特征的基础之上，通过将二者有效结合，应用于评价系统中的不同层级中。通过对各评价指标进行模糊化处理使得不同层级的评价对象不仅包含有关专家学者的理论知识经验而且具有一定的客观性，既降低了个人主观因素的影响，而且避免了全部采用理论分析所引起的计算结果的偏差。文章所建立的评价指标体系具有较强的针对性和全面性，能够涵盖辽宁省水资源管理的关键性参数要素。基于改进模糊元分析的权重计算法表现出良好的精度和稳定性，评价模型表现出良好的适用性和准确性。

[1] 才庆欣. 南票区水资源状况及开发利用分析[J]. 水利规划与设计, 2014(09): 27- 29.

[2] 杜荣海. 辽宁省水资源量情势浅析[J]. 水土保持应用技术, 2016(02): 27- 28.

[3] 汪跃军. 淮河干流蚌埠水文站年径流系列多时间尺度分析[J]. 水利技术监督, 2007(01): 37- 40.

[4] 全占东. 水足迹理论视角下辽河流域水资源评价[J]. 水土保持应用技术, 2017(01): 22- 24.

[5] 黄亮. 水资源可持续发展存在的问题及对策[J]. 水土保持应用技术, 2013(04): 32- 34.

[6] 姜广田, 邓程林. 辽宁省城市饮用水水源地安全评价研究[J]. 水利技术监督, 2008(02): 24- 26.

[7] 徐飞. 沈阳地区水资源短缺原因分析及对策研究[J]. 水资源开发与管理, 2015(01): 24- 26.

[8] 曲锦艳. 辽宁省水资源存在的问题与保护对策[J]. 水土保持科技情报, 2002(06): 16- 17.

[9] 刘启和. 基于辽阳县地下水资源质量评价的研究[J]. 水土保持应用技术, 2016(05): 47- 49.

[10] 程海英. 锦州市城区水资源现状及优化配置方案[J]. 水土保持应用技术, 2015(06): 22- 23+32.

[11] 张永平. 洪水对水质的影响及监测工作初探[J]. 水利技术监督, 2013(06): 1- 3.

[12] 张海军. 水资源保护监测存在问题及建设初探[J]. 水土保持应用技术, 2016(03): 40- 43.

[13] 陈滋月. 气候变化情景模式对流域水土流失影响的定量分析[J]. 水利规划与设计, 2016(06): 32- 35.