例谈物理试题中“质量不计”模型的理解及处理

卢 炜 雷光娟

(1. 江苏省南菁高级中学,江苏 江阴 214437; 2. 江苏省江阴市青阳中学,江苏 江阴 214401)

1 引言

近几年的江苏高考物理试题、模拟试题中常常出现“质量不计”的物理模型,如2011年第9题中的轻质丝绸,2012年第14题中的轻杆等等.我们常常遇到的轻杆、轻绳、轻环、轻弹簧都属于“质量不计”模型,有些题目则直接标明滑轮或木板的质量不计.“质量不计”模型与学生所熟悉的质点不同,质点只考虑了物体的质量,学生可以熟练地使用牛顿第二定律进行处理.部分学生对“质量不计”不能够充分有效的理解,不能够在脑海中形成“质量不计”物体的运动图像及过程,在理解及处理“质量不计”问题的时候出现了茫然.现就近几年在江苏高考试题、模考试题中出现的几个典型“质量不计”模型问题进行分析、探讨.

2 典型例题分析

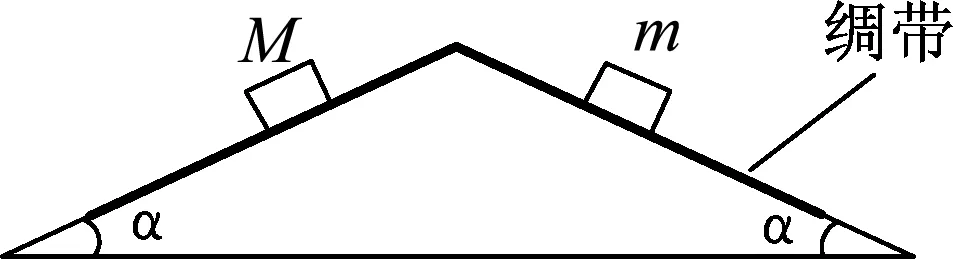
图1

例1.如图1所示,倾角为α的等腰三角形斜面固定在水平面上,一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧,绸带与斜面间无摩擦.现将质量分别为M、m(M>m)的小物块同时轻放在斜面两侧的绸带上.两物块与绸带间的动摩擦因数相等,且最大静摩擦力与滑动摩擦力大小相等.在α角取不同值的情况下,下列说法正确的有

(A) 两物块所受摩擦力的大小总是相等.

(B) 两物块不可能同时相对绸带静止.

(C)M不可能相对绸带发生滑动.

(D)m不可能相对斜面向上滑动.

解析:本题中丝绸为“质量不计”的理想模型.首先取丝绸为研究对象,因为丝绸为轻质丝绸,所以丝绸的质量不计,根据牛顿第二定律F=ma,丝绸受到的合外力为0(否则其a→∞),又丝绸与斜面之间没有摩擦力,只存在两个物块与丝绸之间的摩擦力,所以两个物块对丝绸的摩擦力一定相等,再根据牛顿第三定律,即作用力与反作用力总是大小相等,所以两物块受到丝绸的摩擦力时刻相等,选项(A)正确;物块与丝绸之间的摩擦因数并不知道,当动摩擦因数比较大的时候,或者当α角比较小的时候,最大静摩擦力大于mgsinα,此时丝绸可以相对于两个物块同时静止,选项(B)错误;因为两物块与绸带间的动摩擦因数相等,且M>m,又根据fmax=μmgcosα,所以随着α角增大,mgsinα会首先达到m的最大静摩擦力,再继续增大m就会相对于丝绸滑动,根据(A)选项,两物块与丝绸的摩擦力仍然相等,但是此时摩擦力没有达到M的最大静摩擦力,M仍然相对于丝绸静止,选项(C)正确;当丝绸相对于两个物块同时静止时,M沿斜面向下的分力大于m沿斜面向下的分力,m相对于斜面向上滑动,(D)选项错误;所以选项(A)、(C)正确.

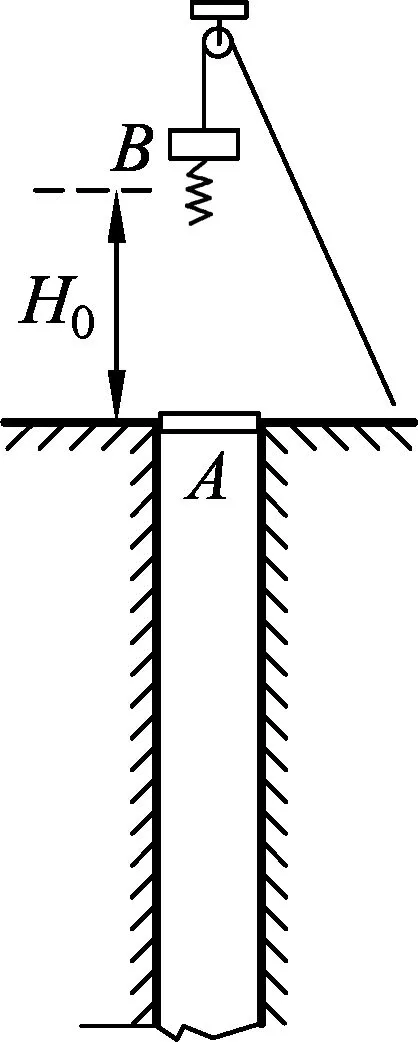
图2

通过本题我们发现对于质量不计的物体,也就是其质量为0,根据牛顿第二定律F=ma,其合外力必然为0.一旦我们知道了其合力为0,那么解题过程也就水到渠成.

例2.打井施工时要将一质量可忽略不计的坚硬底座A送到井底,由于A与井壁间摩擦力很大,工程人员采用了如图2所示的装置.图中重锤B质量为m,下端连有一劲度系数为k的轻弹簧,工程人员先将B放置在A上,观察到A不动;然后在B上再逐渐叠加压块,当压块质量达到m时,观察到A开始缓慢下沉时移去压块.将B提升至弹簧下端距井口为H0处,自由释放B,A被撞击后下沉的最大距离为h1,以后每次都从距井口H0处自由释放.已知重力加速度为g,不计空气阻力,弹簧始终在弹性限度内.

(1) 求下沉时A与井壁间的摩擦力大小f和弹簧的最大形变量ΔL;

(2) 求撞击下沉时A的加速度a和弹簧弹性势能Ep;

(3) 若第n次撞击后,底座A恰能到达井底,求井深H.

解析: 本题中底座A为“质量不计”的理想模型.

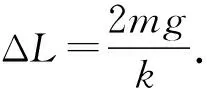
(2) 撞击后A、B一起减速下沉,对B有

mg-kΔL=ma,

解得a=-g.

A第1次下沉,根据功能关系有

mg(H0+ΔL+h1)=Ep+fh1,

解得

(3)A第2次下沉,由功能关系有

mg(H0+ΔL+h1+h2)=Ep+fh2,

解得h2=2h1.

A第3次下沉,由功能关系有

mg(H0+ΔL+h1+h2+h3)=Ep+fh3,

解得h3=2h1+h2=4h1.

同理,A第n次下沉过程中向下滑动的距离hn=2n-1h1.

综上可得，井底深度为

H=h1+h2+…+hn=(2n-1)h1.

本题中有的学生感到不解:A每一次下沉后,B再次回到原位置就会相对于A以不同的高度落下,那就意味着弹簧与A接触的时候有不同的速度,但为什么每次弹簧的最大形变量却是相同的呢?他们这样理解，当弹簧与A相接触,A开始移动的时候弹簧需要减速,而A要加速,他们之间的距离应该进一步缩短,也就是说弹簧的压缩量会变得更大,而B从不同的相对高度下落,导致接触的时候相对速度不一样,从而每次弹簧的压缩量ΔL自然就不一样了.

这里就需要我们弄清楚底座A的“质量不计”的确切含义是什么了.质量不计意味着底座的质量为0.当弹簧撞击到A,“不计质量”的A开始移动后,弹簧继续压缩就会导致A的合外力不为0,根据牛顿第二定律F=ma,对于质量为0的A其加速度就会趋于无穷大,所以弹簧就会瞬间又恢复到原来的形变,故弹簧不会再次压缩.所以在整个过程中只要A动起来了,弹簧的压缩量ΔL就是不变的.

通过本题我们还发现,“质量不计”的物体,当它的合外力为0的时候,其加速度可以是任意的值,具体数值根据具体情况而定,如本题中底座A的加速度与B相同,为-g.

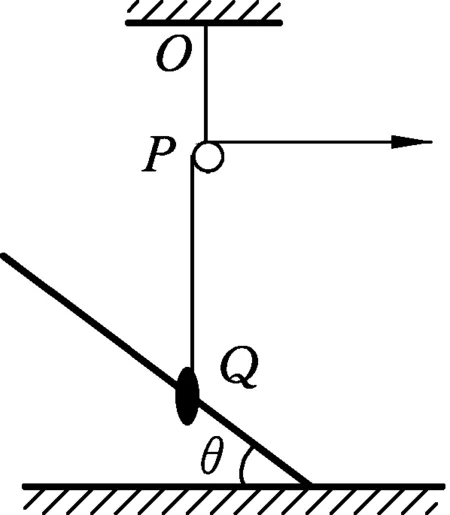
图3

例3.将一光滑杆固定在地面上,杆与地面间夹角为θ,一光滑轻环套在杆上.一个大小和质量都不计的滑轮用轻绳OP悬挂在天花板上,用另一轻绳通过滑轮系在轻环上,用手拉住轻绳另一端并使OP恰好在竖直方向,如图3所示.现水平向右拉绳,当轻环重新静止不动时OP绳与天花板之间的夹角为

(A) 90°. (B) 45°.

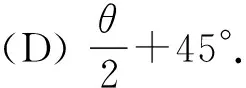
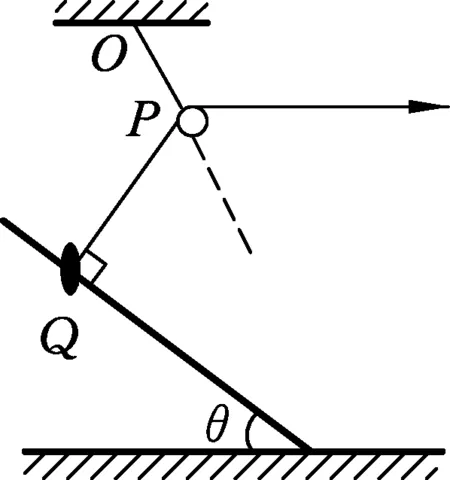
图4

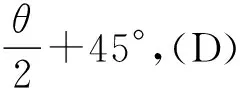
在解这道题目的时候,如果没有注意到环是不计质量的而考虑了环的重力,那么就很难得出正确答案.另外有学生会提出:轻环由Q到PQ垂直于杆的时候是有速度的,为什么能突然静止呢?那么我们就必须搞清楚,轻环是不计质量的,而质量是惯性的量度,所以轻环就不存在惯性.此题中同时出现了轻绳,轻绳同样是质量不计的,而轻绳上的力总是处处相等的.

3 结束语

根据以上例题分析我们对“质量不计”模型做出如下总结:根据牛顿第二定律F=ma,质量不计的物体其所受到的合外力一定为0,在合外力为0的时候其加速度可以为任意值,或者说质量为0的物体的运动状态是任意的,根据具体情况而定,另外质量不计的物体没有惯性.从定性和定量两个方面正确理解“质量不计”的物理含义,能够使得我们简单有效地解决物理问题.

参考文献：

1 胡晓强. 例谈理想模型与实际研究对象间的差异[J].物理之友,2017(4):9-12.

2 钱小敏. 正确理解“质量不计”[J]. 数理化学习,2014(10):71-72.