双气球连通实验变化规律研究
王文涛
(江苏省镇江第一中学,江苏 镇江 212000)
1 问题的提出
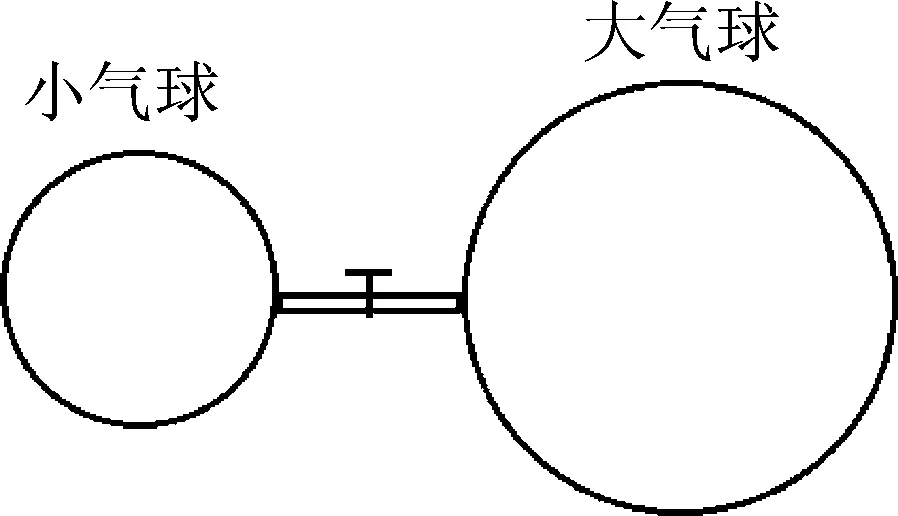
图1
在指导学生做趣味物理实验中,经常做如下实验:将两个相同的气球吹成不同半径大小,用管子将两者连接,打开中间的气阀,观察气球大小的变化.一般预期的实验结果是大的变得更大,小的变小.但学生实验中偶尔也会出现相反的结果.开始认为是学生实验操作错误造成如此的结果,但是消除实验中的错误后,仍然有部分学生的实验结果与预期不同.那么气球大小的变化与哪些因素有关呢?
2 理想圆形气球的附加压强模型
气球的大小变化取决于两侧气球的压强大小,而气球内部的压强由两部分构成,一是外部的大气压强,二是气球壁扩张后产生的附加压强.两气球的外部大气压强相同,所以影响气球内部压强的是气球壁的附加压强.气球的大小不同其附加压强应该有所不同,所以对于同一气球,其附加压强应该与其半径有关.
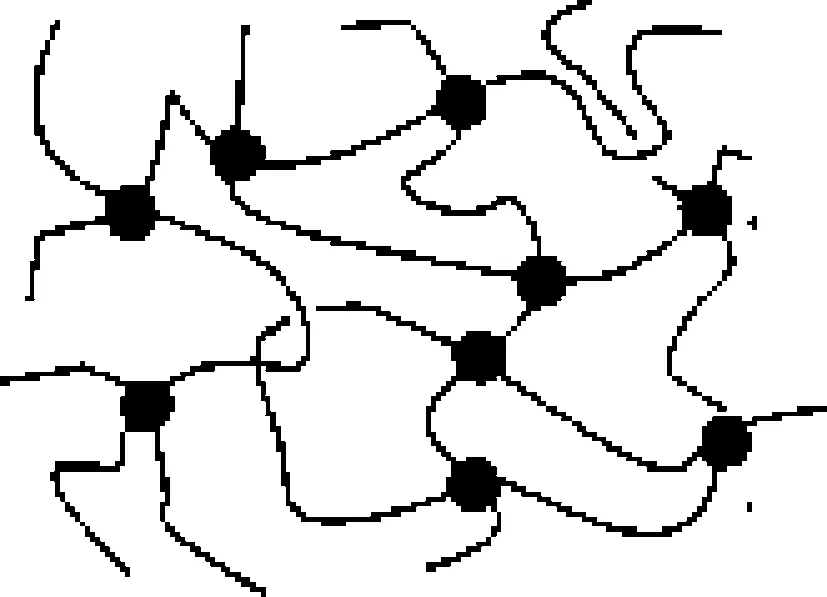
图2 硫化橡胶的分子构型示意图
平时买到的普通气球是利用硫化后的橡胶制作的,其橡胶分子的长链通过硫原子链接在一起,形成三维网络结构,如图2所示.因此,硫化后的橡胶制品具有各方向相同的物理性质,在理论研究中可以视为各向同性的理想弹性体.
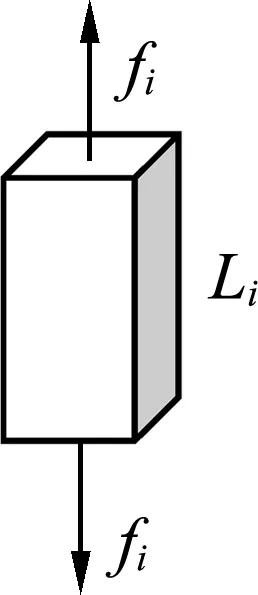
图3
气球在增大过程中,其半径变化较大,气球壁的拉伸较大.因此弹性材料在拉伸过程中其截面大小及长度均发生变化,弹力与形变并不遵守胡克定律.此时必须采用理想弹性体模型才可以描述其弹力与形变之间的关系.根据文献[1]中的弹性体模型理论,一个理想化的矩形截面的弹性体有如下的规律.
(1)
(1)式中的fi是在i方向施加的外部作用力;Li是i方向的长度;k是玻尔兹曼常量;K是常数,与弹性体内部材料组成有关;T是热力学温度;Li0是材料原始长度,p是弹性体内部压强(静压强),V是弹性体的体积.对于理想的弹性体,可以假设在形变中体积V不变.从(1)式可以得出弹性体的弹力与弹性体长度方向形变和内部静压强有关.
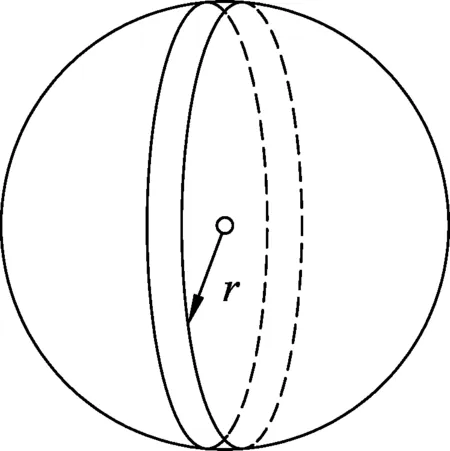
图4 气球上选取的研究面位置示意
如果气球在恒定温度T下缓慢增大,可认为气球壁的温度保持T不变.可以取沿气球大圆的一个窄环面进行研究,如图4所示.
由于气球壁的厚度d相对于气球的半径r较小,其宽度较窄,可将环面展开视为理想化的矩形截面弹性体,如图5所示.
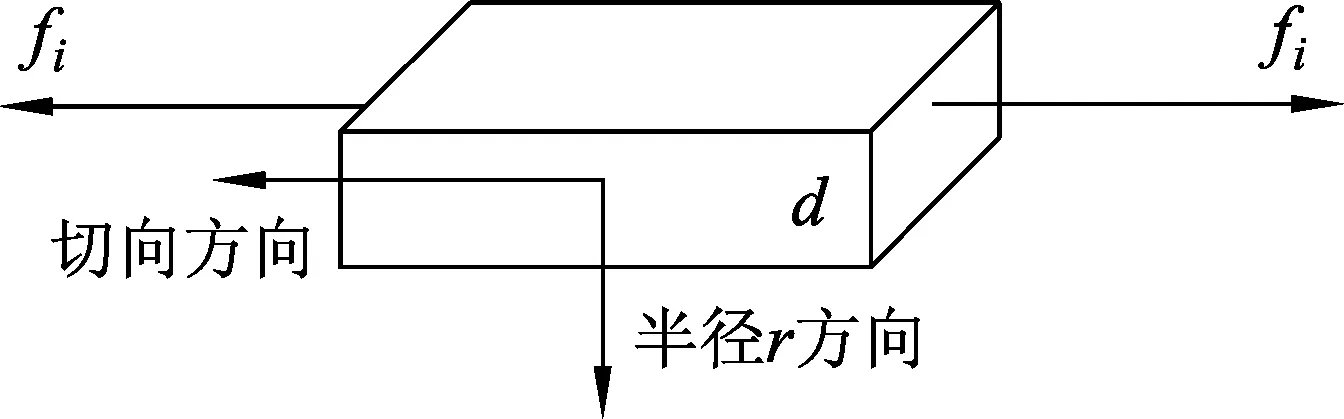
图5 展开后的气球环面
其沿切向的气球壁长度Li与气球半径r成正比,应用(1)式可得,在切向有
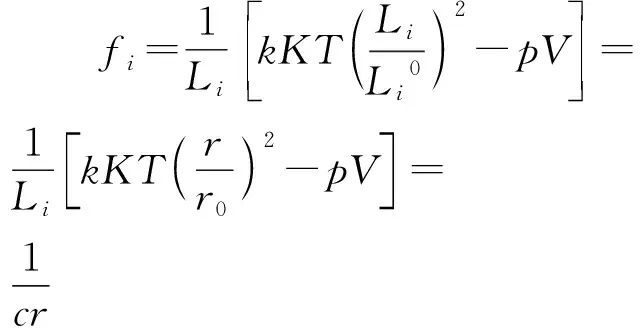
(2)
其中Li=cr,c为常数.
在半径r方向上,由于气球内外壁的压力差可分解为沿切向的作用力,所以沿半径方向不受拉伸或压缩的外力,设气球壁原始厚度为d0,气球膨胀后壁厚度为d,同样运用(1)式可得
(3)
由(2)式可得
(4)
由于气球壁的总体积V0不变,设气球原始半径为r0,膨胀后半径为r,总有
V0=4πr2d=4πr02d0.
可得
(5)
将(5)式代入(4)式可得
(6)
将(6)式代入切向方向的(2)式可得
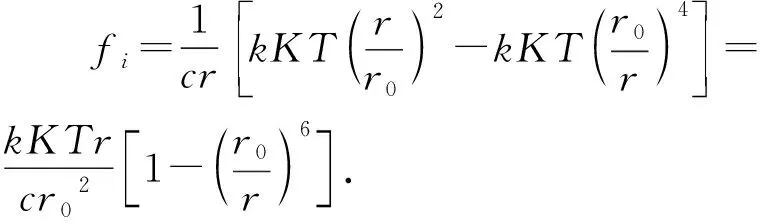
(7)
考虑半个气球的受力有
(8)
(8)式中p为气球内部压强,p0为大气压强,pf为气球壁的附加压强.
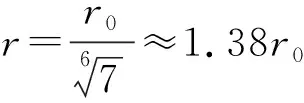
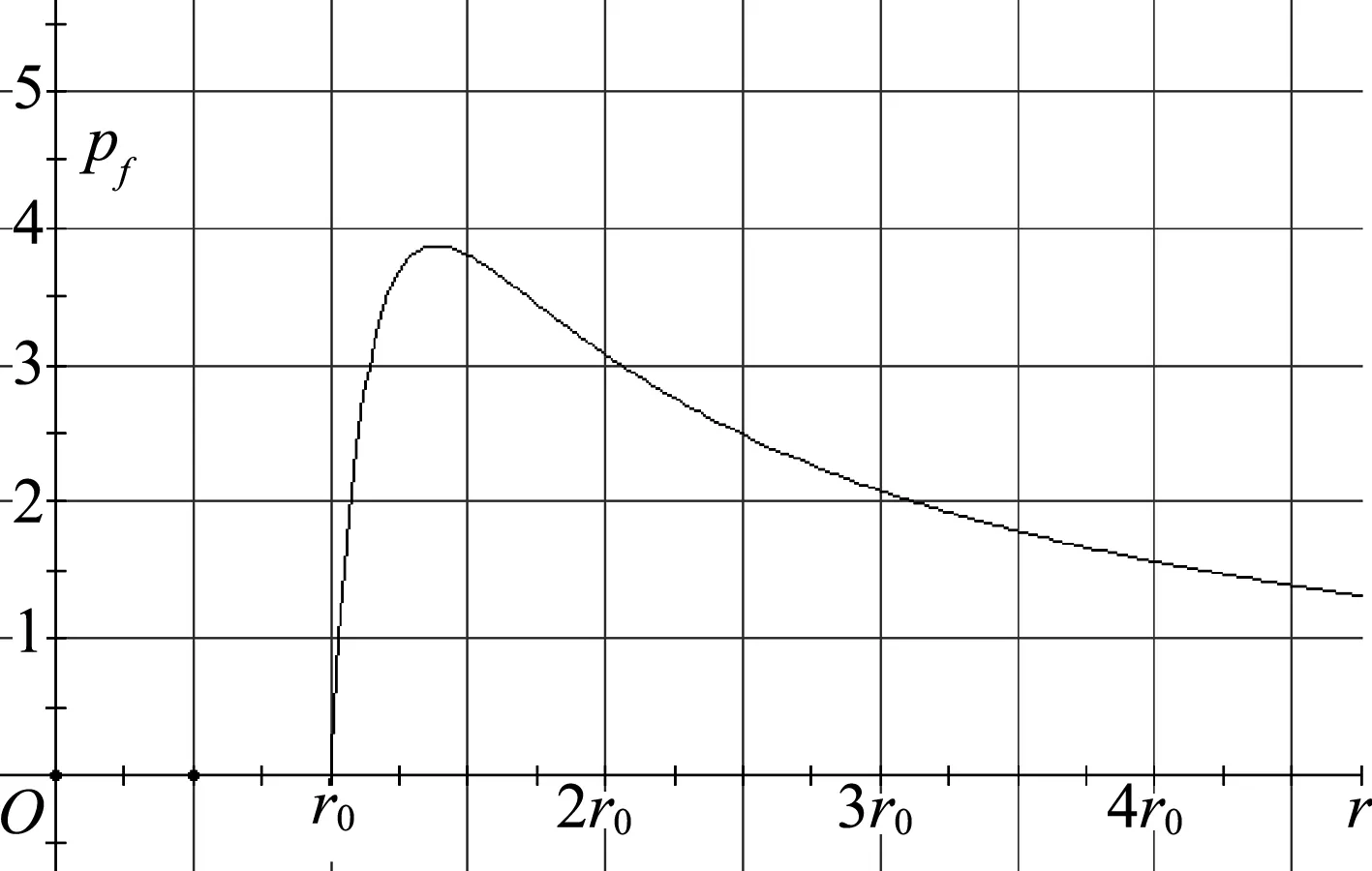
图6
从图6可以看出气球的附加压强pf与半径r的关系并不是单调关系,附加压强pf随半径r先增大再减小,当r趋于无穷大时,附加压强趋于0.
3 实际圆形气球附加压强测定
以上从理论上得出了附加压强pf随半径r变化关系,还需要通过实际实验验证上述理论关系.
实验中需要测量气球的附加压强pf,可以利用气压计测定气球内部压强p和大气压强p0,则pf=p-p0.实验中准确测量气球半径r有些困难,可以转化为通过测量气球体积VB来间接测量气球半径r,为此设计了图7的实验装置进行研究.
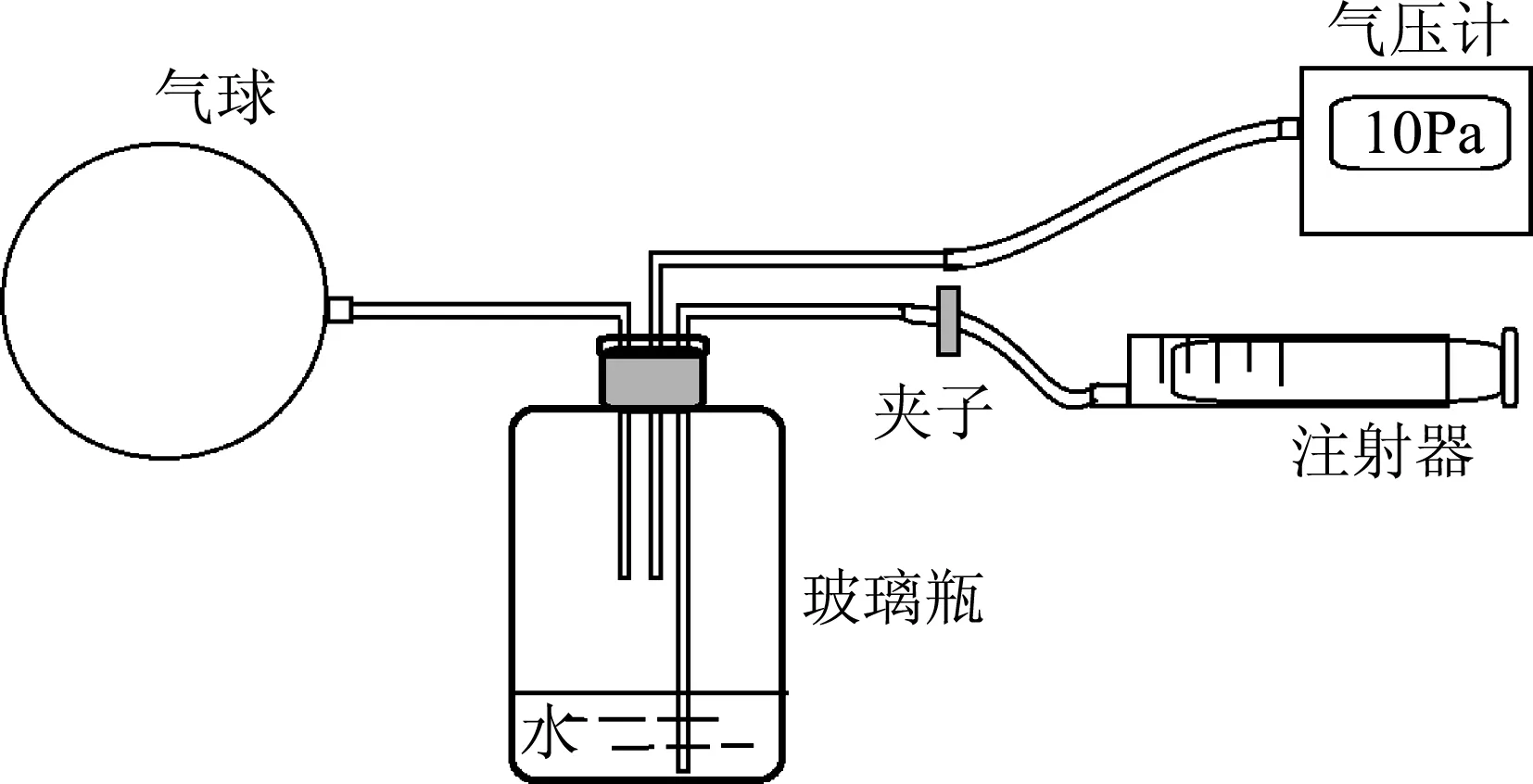
图7 研究气球附加压强实验装置图
设大气压强为p0,V0为玻璃容器中气体的体积,pf为气球内外的压强差,VB表示气球的体积,Vw表示注入水的体积,由于气球缓慢扩大,可以认为气球内部气体是等温变化,根据理想气体方程可得
(p0+pf)(V0+VB-Vw)=p0V0.
(9)
可得
(10)
由(10)式求出VB后,进一步可求得气球半径为
(11)
测量时先将气球中的空气排净,然后扎在管口.玻璃瓶中先做好标记线,标记线上方的体积V0可用注水法测出.每次用注射器吸取一定体积的水注入瓶中,待气球稳定后读出气压计的读数计算出pf.重复多次即可得出pf与注入水的体积Vw的关系,然后可求出pf与r的关系.
选择不同的气球A、B各做两次,A气球的实验数据如图8所示.从图线趋势可以发现气球内附加压强pf与半径r的关系如下.
(1) 气球附加压强与r的图像与理论预测图像相一致.
(2) 气球内附加压强与r不是单调关系,先增大到峰值,然后逐渐减少.
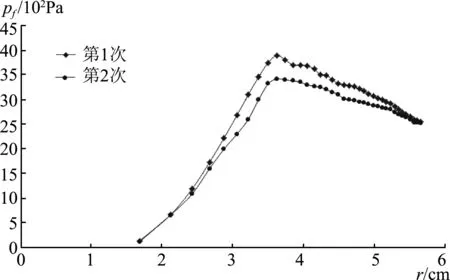
图8 A气球的pf-r图像
(3) 峰值点与预测基本一致.
(4) 新气球第1次的图像要高于第2次及以后的图像.
对于(4)原因可能是第1次实验时气球橡胶材料第1次发生形变,内部橡胶分子长链之间的连接未遭到破坏,所以气球膨胀到同样半径大小产生的附加压强大.第2次实验时,由于内部橡胶分子长链之间的连接已经被破坏了部分,所以导致同样半径产生的附加压强减少,总体曲线降低.
同样的实验方法,对于另一个B气球进行实验测定,其实验图像如图9所示.
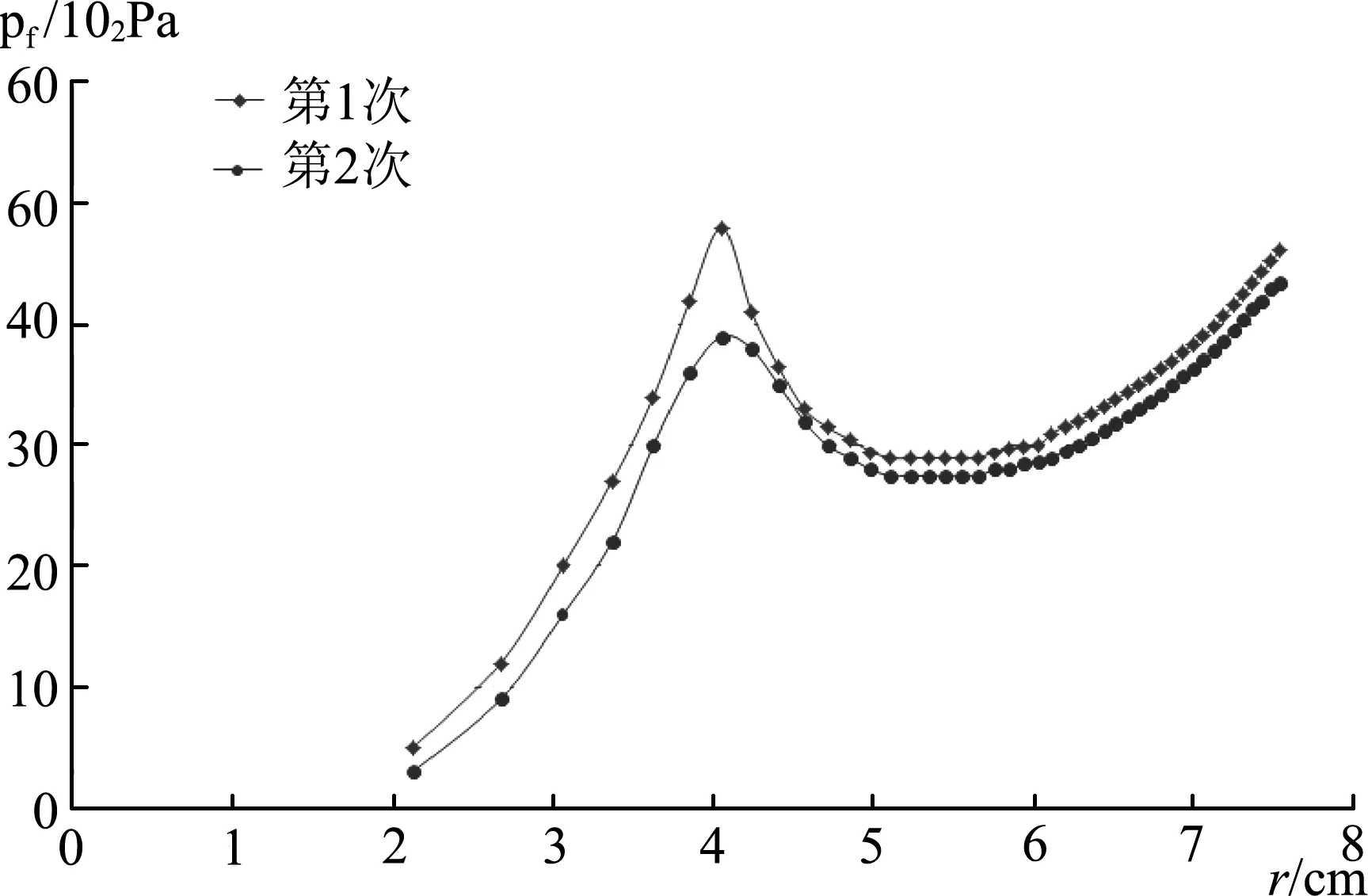
图9 B气球的pf-r图像
与A气球的图像相比,可以发现图像也有另外的特点.
(1) 半径较小时与理论图像相符合.
(2) 当半径增大超过一定值后,出现压强随半径再次上升的现象.
如果将气球壁视为理想弹性体,则根据(8)式pf将随着半径r一直减小,当球半径无穷大时,附
加压强为0,但是实际气球肯定不能无限扩大.从B气球的图像可以看出当气球半径过大,气球壁形变巨大,其内部结构也随之发生变化,气球壁已不可以视为理想的弹性体,原来的理想化模型不能适用.此时随着气体的不断压入,气球形变开始变慢,随之压强迅速增大.如果继续压入空气,其压强超过气球所能承受的弹力时,气球便发生破裂.
4 两气球连通大小变化规律总结
由上述理论和实验结果,可以分析两个相同的气球充气成不同半径,再连通后大小变化情况.一般情况下,不会将气球充气至极限.在气球不太大的时候可以认为气球的附加压强符合理论模型.根据其pf与r的关系可以将气球变化的情况分成3种类型讨论.
如图10所示,可能出现的3种情况结果如下.
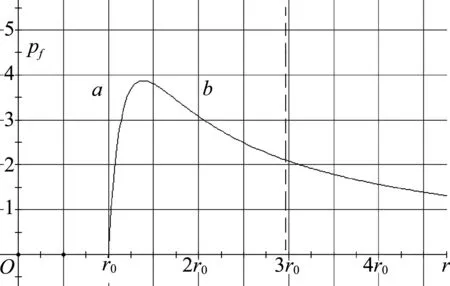
图10 气球变化规律分段
(1) 若大小气球的半径都在a区,则大球变小,小球变大.
(2) 若大小气球的半径都在b区,则大球变大,小球变小.
(3) 若两个气球的半径一个在a区,一个在b区,则情况不定,取决于气球内部压强大小.
因此,在指导学生做趣味实验时,应该保证球的半径不超过b区,即球的大小适中,这样才能实现预想的实验结果.
参考文献:
1 M H. James, E Guth.Simple Presentation of Network Theory of Rubber, with a Discussion of Other Theories[J].Journal or Polymer Science 1949,(IV): 153-182.
2 杨晓翔.非线性橡胶材料的有限单元法[M].北京:石油工业出版社,1999:70-82.
3 I Müller,P Strehlow.Rubber and rubber balloons[M].New York: Springer. 2004:1-31.

