5E教学法在中学物理重心概念教学中的探讨

颜国英 张皓晶 郑原琛 李宝金 张 雄

(云南师范大学,云南 昆明 650500)

1 5E教学法的基本内涵

“三阶段学习环”是R. Karplus基于瑞士心理学家皮亚杰的理论研究而提出的,美国生物科学课程专家对此在实践的基础上,进一步细分形成5个前后密切联系的阶段:引入(Engagement)、探究(Explore)、解释(Explain)、拓展(Elaborate)、评价(Evaluate),故称为5E学习环或5E教学模式,[1]是一种结合构建主义和概念转变理论,强调学生的主体地位,学生在创设的情境中经历概念的引入,再进行各种探究活动,发展经验形成新概念的探究式教学. 5E教学法让学生学会对生活情境运用概念进行实例映射,多维度拓展促进对所学概念的更深入理解,5E教学法最后“评价”阶段,通过教师口头提出开放性问题、书面表达或表现性任务对学生整个学习过程进行正式评价的有效探究教学.

5个阶段的紧密进行体现了学习者基于原有的知识经验生成意义、建构理解的概念构建过程,同时也是引发认知冲突并加以理解消化的过程,是原有的某种知识经验由于受到与此不一致的新经验的影响而发生的重大改变的概念转变过程.

2 运用5E教学法建立重心概念的过程

在中学物理中,一个物体的各部分都受到重力的作用,从效果上看,可以认为各部分受到的重力作用集中的点叫做物体的重心.重心是一个比较重要的概念,与物体的形状和质量分布情况有关.而生活的情景中会遇到有关重心偏离几何中心以及重心发生变化等问题．本文以几个有关重心的有趣物理现象为例,运用5E教学法体现出学生建立重心概念的过程.

2.1 “爬坡的圆盘”引入重心概念

首先通过演示圆盘在斜坡上的运动,创设圆盘爬坡这样一种与原认知冲突的问题情境,引起学生的好奇心和注意力,从而主动参与到本课的概念学习中.圆盘可由食品铁盒a在内部用透明胶等物体固定一重物b制作而成,在演示的过程盖好盖子避免让学生看到内部结构.开始时先以图1[2]中的A状态摆放好,提问学生由静止释放后圆盘会如何运动,学生根据先验经验会回答沿斜面滚下,结果发现圆盘向上“爬坡” 依次经过B、C后在B点静止;再以B状态摆放好,提问学生猜想圆盘会如何运动,学生回答后由静止释放圆盘进行演示,结果发现圆盘只会轻微摆动仍停留在B处;最后以D状态摆放好同样进行演示,结果发现圆盘会向下滚动依次经过C、B、A最后向上滚动停留在B处.学生在每一次演示之前的猜想都极有可能是错误的,通常在观察后仍不能说明为何会有如此神奇的运动现象,顺势引入重心概念.

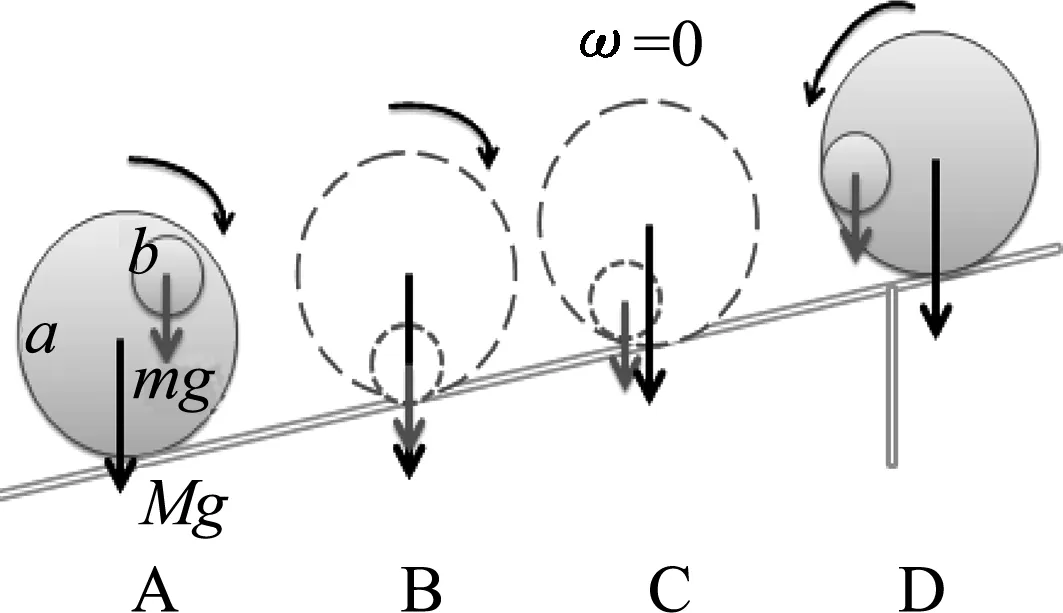
图1 “爬坡的圆盘”示意图

5E教法依据:5E教学法中“引入”环节意味着学生应该在知识产生的真实情境中,通过与教师、同伴的互动,学习建构新知.在这一环节中,教师需要通过创设情境,设计一些引入活动来吸引学生的注意力.这些引入活动中有一部分与当代普遍认可的新经验一致.而有一些是不一致的.[1]由“爬坡的圆盘”创设的问题情境在很大程度上与学生当前的认知造成了极大的冲突,可以引起学生强烈的求知欲从而达到了引入重心概念的演示效果.

2.2 深入探究“多变的几何板”

教师给学生提供探究教具:正六边形硬纸板若干、沿正六边形对角线剪下的硬纸片若干、挂有10g钩码的重垂线以及双面胶若干.

(1) 组织学生以小组合作形式探究不同形状、质地均匀的几何硬板重心,教师示范说明两次悬挂法的具体过程,学生进行操作探究,分析两次悬挂法确定重心的合理性,最后总结操作步骤如图2中的A:用重垂线与几何纸板于同一点悬挂后,在纸板上画出重垂线的路径,改变悬挂点再画出一条重垂线的路径,两线交点M即该纸板的重心;总结出探究结论:质地均匀的物体其重心位于几何图形的中心.

(2) 组织学生按照图2中将正六边形沿K1、K2对角线对折后用双面胶固定好,就制成了质地不均匀的五边形纸板(如图2中的B),学生继续探究该纸板的重心.提出问题学生讨论:如何判断B图形质地是否均匀?该纸板是否是轴对称图形?重心有何特点?在探究交流后,学生基本能区分出何种物体是质地均匀的,对于轴对称的物体,重心必落在对称轴上的一点，如图2中的B图形重心N，必落在该图形对称轴上.

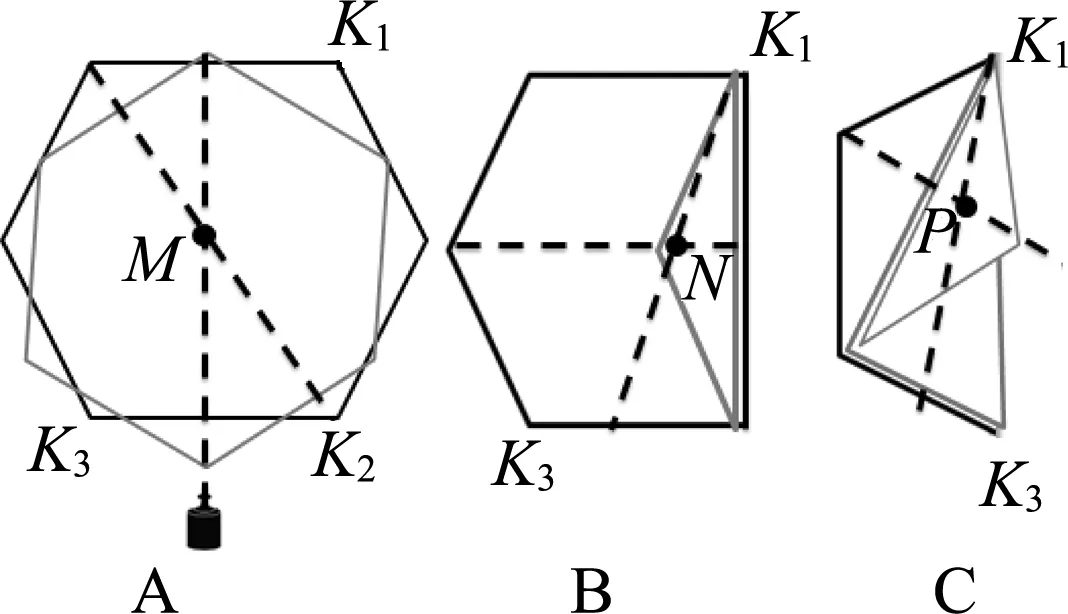
图2 “多变几何板”的变换过程

(3) 组织学生将上述B图五边形纸板再沿对角线K1K3对折,变成既不是对称又不是质地均匀的C图形纸板,探究该图形的重心.提出问题学生讨论:如何判断C图形质地是否均匀?该纸板是否是轴对称图形?重心有何特点?学生总结出质地不均匀的不规则图形的重心位置无明显规律特点，但可通过两次悬挂法找出重心位置，如图2中的C图形重心P.此处操作是对两次悬挂法寻找重心的强化练习.

5E教法依据:以上探究活动始于学生对课前引入的兴趣,激发了学习探究的动力,因而学生具有较大的主动性符合探究的科学发展观.探究活动各环节由浅入深层层递进,能够让学生充分调用已有知识和主体能动性开展探究,各环节紧密关联又有新的挑战,符合学生已有知识的元认知结构以及最近发展区理论的要求.“探究”是整个5E教学模式的中心环节,获取知识、掌握技能和技巧都是在这个过程完成的.[2]

2.3 解释明确重心概念

根据以上的实验探究结果,教师鼓励学生对操作的经验、概念的理论化以及思维的过程等进行多维度的分析、解释.出声思维就是要让学生将其思维过程充分展示出来,借助于语言向老师或同学吐露其内隐的思维过程.因此,解释的过程能够更好地暴露学生对于多变的几何板重心测量的迷思概念以及低效思维方式,学生能够及时形成正确的概念并且将零散的知识整理成系统化认知结构,形成正确的物理观念,培养学生的核心素养.[3]

2.4 制作“双锥体爬坡” 拓展多维学习

在高中《物理·必修 1 》中通过观察与思考双锥体沿斜面轨道上滚的现象,使学生加深了解在重力场中物体总是以降低重心,趋于稳定的规律运动.[4]双锥体上坡的演示实验装置有实验室的专业装置,也有用篮球和竹竿等改进的装置.本文介绍一种让学生用生活中常见的一次性纸杯就能制作的双锥,如图3,用两个纸杯在开口处用透明胶连接好制成“双锥”,轨道可以用光滑的金属棒或者木棍制成.[5]演示双锥爬坡:开始时双锥放在距离较小的轨道e内,再慢慢向外移动两边轨道到达f处,结果发现双锥由G1处运动到了H1处,距离斜坡最高点更近了,此过程看起来双锥在爬坡.教师提供纸杯、透明胶、木棒等让学生动手制作双锥,学生尝试使双锥运动到“坡顶”并在上述学习的基础上找出双锥的重心以及重心的运动轨迹,分析该现象产生原因.提出问题学生讨论:若将两个杯子底部相连接,应如何移动轨道使其“爬坡”?

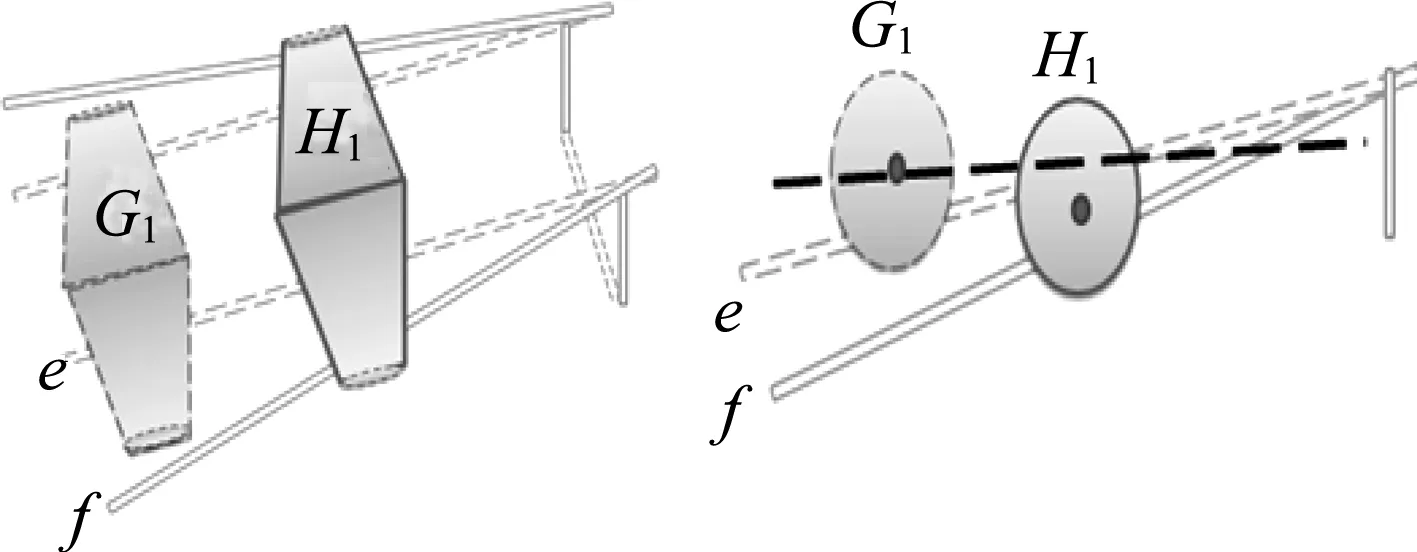
图3 双锥爬坡演示图及其前视图

由图3的前视图可以发现:G1处双锥半径较大,重心所在的直线到导轨的距离较大,即重心高;在轨道变宽后,H1处双锥半径小,重心较低,故双锥爬坡的过程实质上是重心向下运动的过程.若将两个杯子底部相连接制成双锥,则轨道应由宽变窄才能使双锥“上坡”,其原理相同.

5E教学法依据:拓展环节主要包括两个方面的内容.一是拓宽知识面,二是学以致用,这是学生把所学知识不断精致化的过程.[6]双锥爬坡的现象学生可能通过生活中的民俗游戏接触到,学习这部分内容,不仅是一个动手操作的知识应用过程,更是对我国优秀传统文化的学习、传承过程.

2.5 嵌入课堂的评价

嵌入课堂,即说明课堂评价具有教学意义,是一个教学事件的特殊表现形式,评价始于教学,为了教学.本次探究学习的课堂中,教师可通过学生对探究的反馈、学生的自我评价和同伴评价,开展本次评价,或者通过口头提出开放性问题:学生分析如图4“翻筋斗的魔丸”的重心变化过程进行非正式评价.

5E教学法的评价理论与我国新课程理念下的评价相契合:主体由教师主导到师生共同参与,评价手段从单一的形成性测验到正式和非正式评价方法相结合,评价功能从只对学生学习结果查漏补缺到持续支持学生学习再到改善教与学.

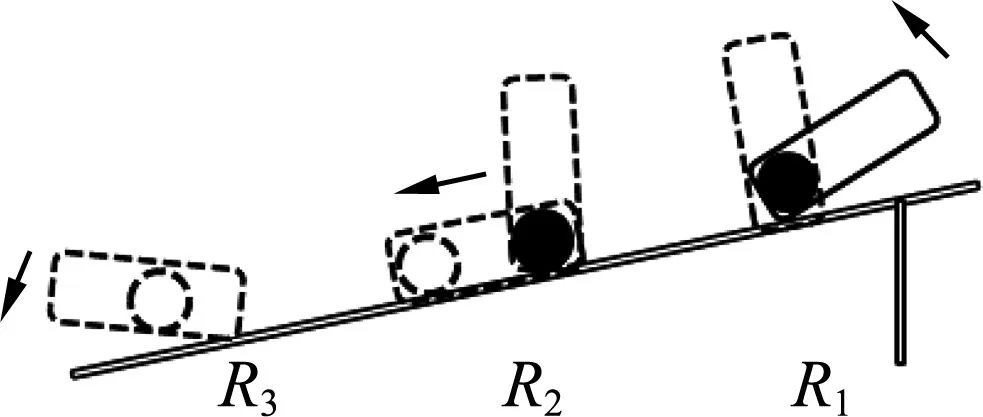
图4 “翻筋斗的魔丸”重心变化示意图

3 讨论

本文讨论了5E教学法的各阶段在重心概念建立过程的渗透,结合有关重心概念的几个易引起认知冲突的例子,贯穿阐述了5个阶段教学法的设计理念和教学依据,从简明的原理图中进行形象生动的分析,有利于学生重心概念的建立以及探究能力的提升.各环节末尾从理论基础、教学目标和基本特征3个方面讨论了5E教学法和我国探究式教学的联系,为我国中学物理探究教学的发展寻找新的动力.文中的例子在教学中的实用性很强,不仅是因为实验现象非常明显,更是因为实验现象与学生的认知存在一定的冲突,给学生以极大的好奇心和求知动力,探究过程有利于发展学生的动手操作能力和科学素养,在此希望能为其他知识的教学提供有效借鉴.

参考文献：

1 李娜.基于5E模式的中学物理教学研究——以《物体的沉浮条件及应用》为例[J].物理教学探讨2014(5):5-8.

2 B Nuri. Teaching torque with 5E learning strategy: an off-center disk case[J].Phys. Educ. 2018(53)： 013001.

3 桑蕊蕊.浅谈5E教学法促进物理观念的深刻转变[J].物理通报，2017(8):111-115.

4 张瑛.双锥体上坡实验的改进[J].物理通报.2016(5):78-79.

5 B Nuri. New versions of the rolling double cone[J]. Phys. Teach. 2002(40): 156-157.

6 廖伯琴.初中物理教学策略[M].北京:北京师范大学出版社,2010:66-69.