基于语义的政策血缘网络演化机理研究
刘 刚,傅玮萍,马莺歌
(哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
0 引言
中国社会保障政策体系逐渐趋于碎片化发展态势,导致了城市社保制度与农村社保制度的互相割离,私有经济以及与国有经济社会保险制度不同,多种社会保险政策同时生效的不良状况[1]。为有效地缓解并预防社保政策中的碎片化现象,本文通过分析政策碎片之间深层的内在联系,实现碎片化政策的重新组织。在此基础上对结构化的政策网络进行碎片消解,使政策网络结构更加明晰。除此之外,本文基于结构化的政策网络,在新政策的制定过程中,对碎片化政策的产生加以预防。本文所提出的政策分析与制定计算机仿真技术,可以帮助决策者清晰看到政策的体系结构,并预测新政策在该政策体系中的地位,为有效地消减和预防政策碎片化现象提供有效的解决方案。
1 相关工作与理论基础
1.1 相关研究工作
1.1.1 国内外研究现状
政策网络研究起始于20世纪90年代初,几位数学科学家及诺贝尔奖获得者共同提出了政策系统的网络结构及其特征。发展到目前,主要有三种研究方向: 英国传统、美国传统以及荷兰和德国传统[2]。T.Lowi、H.Heclo等美国学派研究者着眼于政策网络的微观层次,通过模拟政策在制定的流程节点间的互动,来分析预测政策制定和执行的效果及网络的形态演化。而英国传统将分析重点放在不同政策部门之间的结构关系上。从政策体制本身入手,分析政策网络的拓扑结构及影响。以荷兰、德国领域专家为首的学者从宏观层次上进行政策网络理论研究,将政策网络看成一种全新的国家治理手段[3]。
我国政策网络理论研究起步较晚,近些年开始逐渐流行,成果较少。目前,只有很少的政策网络理论成果问世[4-5]。文献[6]对政策网络的方方面面进行了细致而又全面的介绍,包含: 政策网络起源、政策网络的不同释义、政策网络要素及其作用、政策网络的研究意义,以及具体的政策网络的理论研究手段。然而,不同派别的研究人员对于政策网络理论的认识并不统一,对于政策网络中的基础定义各执一词。鉴于此种情况,系统深入地研究政策网络理论是十分重要的[7-8]。
政策血缘挖掘理论是政策网络研究的一个新方向。文献[9]形式化地定义了政策族谱树的概念,用于描述显性的政策体系树状结构,在此基础上形成了政策森林的概念。该理论的基本思想是,挖掘政策体系中不能从政策族谱树中体现的政策碎片之间的隐藏关系。并称这种关系为隐性政策血缘关系,称不同政策中形成这种隐性政策血缘的因素为隐性政策基因。
文献[10]利用隐性政策血缘挖掘理论,阐述了一种有效的隐性政策血缘关系的挖掘方法。将隐性基因引入文本进行相似度计算中,从而发现了常规政策语言相似关系探究手段所无法提取的隐性政策血缘关系。除此之外,文献[11]在文献[10]建立的政策网络基础上,利用节点的介数计算,挖掘政策血缘网络中的显性政策要点。通过对网络政策血缘的传播演化规律进行探索,实现了基于网络政策血缘负载模型的建立。基于该负载模型,定义并计算政策血缘网络中节点的脆性度,并据此进行衡量政策血缘网络里网络节点的重要度,从而挖掘出网络中的脆性点。
1.1.2 现存理论的不足
尽管上述理论从不同方面对政策进行了深入的研究,并取得了丰富的研究成果。然而针对政策碎片化问题时,上述方法仍存在着如下不足:
(1) 政策模型分析。政策模型分析主要通过基于Agent进行政策实施环境建模,通过政策与政策执行环境之间的互动,研究分析政策的执行效果,以及环境对政策延边的影响。然而这些研究方法是从政策外部对政策进行分析,并未深入剖析政策内部深层的层次结构。面对政策碎片化问题时,只能分析碎片政策对社会的影响,并不能分析或解决政策碎片化对于政策系统本身带来的影响。
(2) 政策网络分析。政策网络分析将政策体系看作复杂网络系统架构,是从复杂网络系统演化的角度上研究政策系统本身的演变过程,并通过演化算法预测政策体系未来的发展趋势。政策网络分析方法网络的构建,完全抛开了现实世界的真实网络,只是通过演化生成网络与实际网络进行对比校正网络演化模型及其参数。除此之外,面对政策碎片化问题,只能预测政策系统的碎片化趋势,并不能有效地提出解决并预防政策碎片化现象。
(3) 隐性政策血缘理论。该理论基于真实政策网络,对其结构进行深层挖掘。并在此基础上对政策节点的重要性以及脆弱性进行了深层的研究。然而该理论中并未提出针对建成的网络进行碎片化的治理与防护的措施,这使得该理论对于政策碎片化问题的解决显得不够完善。
本文从上述结论出发,立足于现阶段的已有研究成果,提出一种全新的政策分析方法。本方法基于隐性政策血缘理论,引入政策文本处理的语义理解,并基于“知网”的政策词语相似度和依存句法分析算法,实现政策血缘网络的构建。在此基础上,基于层次聚类思想,提出政策血缘网络层次演化方法,提取政策血缘网络的树状结构,并在此结构基础上提出新政策的判余与位置锁定。
1.2 政策血缘理论
深入研究新中国成立后的政策体系演化过程,可以发现,所有政策均由宪法衍化而来,因而目前所有有效或已失效的政策都因与宪法之间的祖孙关系而存在内在的联系,称之为政策血缘关系。例如,在我国的社会保障体系中,政策之间的政策血缘关系如图1所示。
图1中所展示的即为一颗政策族谱树,它描述了图中节点的父子关系。由图可知,树中路径距离较远的政策节点之间的血缘关系应当较为薄弱[10]。

图1 中华人民共和国社保体系结构示意
1.2.1 政策基因
家族政策通过家族基因来传播和继承政策血缘关系[11]。同理,政策族谱树的衍化过程中传递的主要内容便是政策基因。政策基因具体到以自然语言书写的政策文本中,即可以是政策概念、政策词语、政策条款、政策段落或政策篇章,视具体情况而定。
1.2.2 政策血缘网络
正是政策之间隐性血缘关系的存在,使政策谱系树中不同的分支之间存在了或强或弱的联系,形成网状结构,称之为政策血缘网络,这种网络以政策文本为网络顶点,政策文本之间的血缘关系作为边,两个政策文本间的相似度作为权值,下面进行形式化定义,如式(1)所示。
G=(V,E,W)
(1)
其中,V是顶点集合,该集合有限非空,V中的每个节点代表真实政策系统中的政策文本。E为边的集合集,任意ej∈E(G),使得ej=(vi,vj),且ej=(vi,vj)表示政策网络节点之间的政策血缘关系。顶点之间的相似度W为网络中边的权值。
1.3 复杂网络聚类方法
复杂网络从本质上讲是具有一定特性和拓扑复杂性的图,一个由著名学者钱学森提出的较为严谨的定义为: 如果一个网络具有自组织、自相似、吸引子、小世界以及无标度中的部分或全部性质,则该网络是复杂网络[12]。
聚类分析是将所需处理的数据对象的集合按照它们的相似度分成多个聚类簇或数据对象子集的过程,是一种常用的数据挖掘方法。
文献[13]综合上述分类方法,对聚类算法进行如图2所示的分类,并对每一类聚类算法进行简要介绍。图2中,根据聚类算法是否需要在聚类之前输入参数,将聚类方法分为参数方法和非参数方法。在参数聚类方法中,又可分为软聚类方法(模糊聚类方法)、划分聚类方法和基于模型的聚类方法。

图2 聚类方法分类
2 政策血缘网络体系构建
2.1 政策血缘网络体系
观察中华人民共和国人力资源与社会保障部官方网站中公开的社保相关政策体系,该体系中将社保政策分为八大类,其主要组织形式如图3所示。

图3 社会保险政策体系
对于上述不同类别的政策子系统,其内部又可根据不同的侧重分出不同的子类,每个子类包含若干相关政策。有些政策的组织形式是彼此隔离,互不相关的。从内容上来讲,它们或实施的受体相似或相关,或实施办法相似或相关,这种联系并没能从政策族谱树中体现,这就是政策间的隐性血缘关系。挖掘这种政策间的隐性血缘,并根据这种天然的联系构建隐性政策网络,将是解决政策碎片化问题的有力工具。
政策血缘网络是一个由微观、中观、宏观三个层面构成的政策网络体系。其中,微观层次的政策血缘网络是从政策基因的角度上来考虑的;中观政策血缘网络是从政策细胞的角度上来考虑的;而宏观政策血缘网络是从政策文本的角度上来研究政策血缘网络。
定义1(政策个体) 对于政策文本集C={L1,L2,…,Ln},C所包含的每一个独立的政策文本Li即为一个政策个体。
定义2(政策细胞) 对于政策文本L={M1,M2, …,Mn},L所包含n个政策条款M1,M2, …,Mn即为组成L的n个政策细胞。
定义3(政策基因) 对于政策细胞M={S1,S2, …,Sn},M所包含的m个政策词语S1,S2, …,Sn即为M的m个政策基因。
政策细胞作为政策个体的基本单位,是政策个体所携带信息的最小单位载体,而政策基因作为政策细胞内的遗传物质对于政策细胞的形态以及功能特点起到决定性的作用,进而决定对政策个体的形态以及所携带的信息。
将《中华人民共和国社会保险法》的第二章 “基本养老保险”的前两句和第三章“基本医疗保险”的前两句分别当作两个政策个体,如表1所示。那么对于政策个体L1,组成它的政策细胞为L1M1和L1M2,L1M1和L1M2任何政策条款的改变都会直接引起政策个体L1结构上的改变。而对于政策细胞L1M1={S1,S2,S3}={基本,养老,保险},S1,S2,S3分别是对政策细胞产生决定性作用的组成部分。

表1 政策个体的一个例子
综上所述,政策血缘网络体系的结构如图4所示。

图4 政策血缘网络体系结构示意图
首先对于三层政策血缘网络体系加以形式化定义:
定义4(三层政策网络) 微观政策网络Snet(V1,E1,W1),中观政策网络Mnet(V2,E2,W2)及宏观政策网络Lnet(V3,E3,W3),它们都是加权无向网络,其中:
网络节点的集合分别为V1={S1,S2,…,Sn},V2={M1,M2,…,Mn},V3={L1,L2,…,Ln},其中Si为政策基因,Mi为政策细胞,Li为政策个体;边的集合都表示为E={e1,e2,…,em},集合中的元素分别描述了节点间的相似关系;边的权值的集合表示为W,集合中元素为边所连接的节点对应的政策基因(政策细胞或政策个体)间的相似度值。
明确了由微观到宏观的三层政策血缘网络,下面可以形式化定义政策血缘网络体系的概念:
定义5(政策血缘网络体系) 政策血缘网络体系可形式化为PNS=(Lnet,Mnet,Snet,R(L,M),R(M,S)),其中: (1)Lnet,Mnet,Snet依次分别为宏观,中观和微观政策血缘网络;(2)R(L,M)={e1lm,e2lm, …,enlm}为宏观政策血缘网络与中观政策血缘网络之间的边的集合,集合内元素eilm表示宏观政策血缘网络节点Lp对于中观政策血缘网络中节点Mc的包含关系(Lp,Mc, weight);(3)R(M,S)={e1ms,e2ms, …,enms}为中观政策血缘网络与微观政策血缘网络之间的边的集合,集合内元素eims表示中观政策血缘网络节点Mp对于微观政策血缘网络中节点Sc的包含关系(Mp,Sc, weight)。
2.2 网络体系构建的关键技术
政策血缘网络体系的构建主要包括体系中节点的发现,节点间关系的挖掘,节点间关系权重的计算。其中,政策血缘网络体系中的节点包括政策个体、政策细胞以及政策基因。政策个体即政策篇章,政策细胞为政策篇章中所包含的政策条款,而政策基因则为政策条款中的政策词语。本文规定,政策篇章中的每句话作为政策条款。而获取政策基因的关键在于对政策文本进行分词,因此政策血缘网络体系构建的节点发现主要依靠基于标点的政策条款获取和政策文本分词技术来实现。
政策血缘网络体系中主要存在两种类型的边: (1)网内边: 各层网络内部节点之间的边;(2)网际边: 联通不同层次网络之间的边。每个下层节点都存在一条指向上层节点的被包含关系的边。网际边的权值由如下公式计算,对于上层节点i,以及下层节点j,联通i和j之间边的权值为:
(2)
政策血缘网络体系中,边的挖掘以及权值计算主要分为两部分,其一是网际边的权值计算,这项工作可由式(2)实现;另一部分则为网内边的权值计算,具体到三个层次的政策血缘网络。微观网络的网内边权值由政策基因相似度计算得来。中观网络的网内边权值由政策条款的相似度计算得来,宏观网络的网内边权值由政策个体的相似度计算得来,实现了上述过程,便可实现政策血缘网络的构建,其构建过程如图5所示。

图5 政策网络体系构建流程
图5中,政策血缘网络体系的构建主要分为两个步骤。首先根据宏观网络中政策个体包含条款的数量建立宏观网络与中观网络之间的网际边,网际边的权值由公式(2)计算。依次通过中文分词,依存对提取算法,计算每个政策细胞内部包含的政策基因数量,根据公式建立中观网络与微观网络之间的网际边。至此体系框架构建完成。
然后,基于《知网》的词语相似度计算方法[14-15],实现政策基因的相似度计算,得到微观网络中网内边的权值;利用依存句法分析方法[16-19]对政策细胞进行句法分析,将政策细胞间的相似度计算转化为政策细胞句法分析树之间的相似度计算,从而利用句法分析树匹配的方法[20]实现政策细胞相似度计算,得到中观网络中网内边的权值;基于向量空间模型[21]将政策个体表示为政策细胞的特征向量,将两个政策个体所包含的政策细胞之间相似度的期望作为政策个体的相似度值,从而得到宏观网络的网内边权值。整个政策血缘网络体系的构建,算法如下:

算法1 政策血缘网络体系构建算法输入: 政策个体集合C={Text1, Text2,…, Textn}输出: 政策血缘网络体系PNS=(Lnet, Mnet, Snet, R(L, M), R(M, S))PNS=(Lnet, Mnet, Snet, R(L, M), R (M, S))for 每一个 政策文本Texti in C { Li=Texti; Lnet=Lnet∪{ Li} 根据标点符号, 提取Li中的政策条款Li={item1, i-tem2, … , itemn} for 每一个政策条款 itemj in Li { Mj= itemj; R(L, M)=R(L, M) ∪C (Li, Mj, 1/l); Mnet=Mnet∪Mj 对Mi进行分词,得到政策基因序列Mj={word1, word2, … ,wordm} for 每一个政策词语wordk in Mj{ Sk=wordk; R(M, S)=R(M, S)∪C (Mj, Sk, 1/m); Snet=Snet∪Sk } } }for Li, Lj in Lnet{ for Mi in Li,Mj in Lj{ for Si in Mi,Sj in Mj{ 计算并返回Sim (Si, Sj) Snet=Snet∪Sim (Si, Sj) } 计算并返回Sim (Mi, Mj) Mnet=Mnet∪Sim (Mi, Mj) } 计算Sim (Li, Lj) Lnet=Lnet∪Sim (Li, Lj)}
3 政策血缘网络体系结构演化
3.1 宏观政策血缘网络的层级划分
通过第二节的叙述,实现了政策血缘网络体系的构建。该体系使从微观、中观和宏观三个不同的角度观察政策血缘网络体系的结构成为可能。无论从哪个角度来看,政策血缘网络都是没有层次的扁平化网络。当面对越来越严重的政策碎片化问题时,仅仅依靠该网络体系并不能对政策的碎片管理和消减产生直接贡献。解决政策碎片化问题的关键是对宏观政策网络进行层级划分,实现同功能政策的替代或分解,减少平行政策数量。因此,本文提出应用划分聚类方法,实现政策网络节点的聚类,从而延缓碎片化。
3.1.1 自底向上的层次聚类方法AGNES
自底向上的层次聚类的基本思想是,对于待聚类数据集合,首先将集合中的每一个数据都看做是一个类,然后根据一定的计算标准计算不同类之间的相似度,合并相似度满足要求的类,形成新的类,照此过程进行迭代,直到数据集中所有的数据都合并到一个大类中。其主要步骤描述如下:
(1)首先把数据集合中的每个数据初始化为一个初始类。(2)对于每个类,利用既定的相似度计算方法,两两计算不同类之间的相似度。(3)选择相似度符合实验法要求的类,将这些类合并为一个类。(4)重复步骤(2)~(3),直到数据集中所有的类聚集都凝聚为一个大类。
AGNES算法是一种硬聚类方法,每个类中的节点只明确的归属于一个类,这必将导致某些节点间相似关系的忽视。除此之外,AGNES算法中只考虑了节点之间的相似关系,并未考虑节点之间的包含关系。在实际的政策网络节点中,其政策个体可能是另一个政策的子政策。AGNES中,某个类一旦形成,那么该类中的任何节点将永远从属于该类,并不能随着该类节点的增多而偏移向其他的类。如果某个合并的决策在后来被证明是不好的选择,在AGNES算法中是无法退回并修正的,这将导致聚类结果的偏差愈加增大。为此,本文提出一种新的层次聚类方法PBNAP(Policy Blood Network Architecture Partition)。该方法基于AGNES算法思想,并加以改进,适用于在政策血缘网络的基础上进行网络层次划分。
3.1.2 宏观政策血缘网络层级划分算法PBNAP
政策细胞指政策条款,政策个体指包含了多个政策条款的政策篇章。政策细胞的相似度采用基于依存句分析及依存树匹配相结合的方法,而政策个体间的相似度值是政策细胞相似度的期望值。由于政策个体中包含了政策细胞,故两者的相似度值可以进行比较,从而定义政策个体的相异度如下:
对于政策个体L1和L2,其相似度为Sim(L1,L2),设L1所包含的所有政策细胞中,与L2中任意节点间相似度都小于Sim(L1,L2)的节点个数为nsub,则称nsub与L1的比值为L1相对于L2的相异度。形式化定义如下:
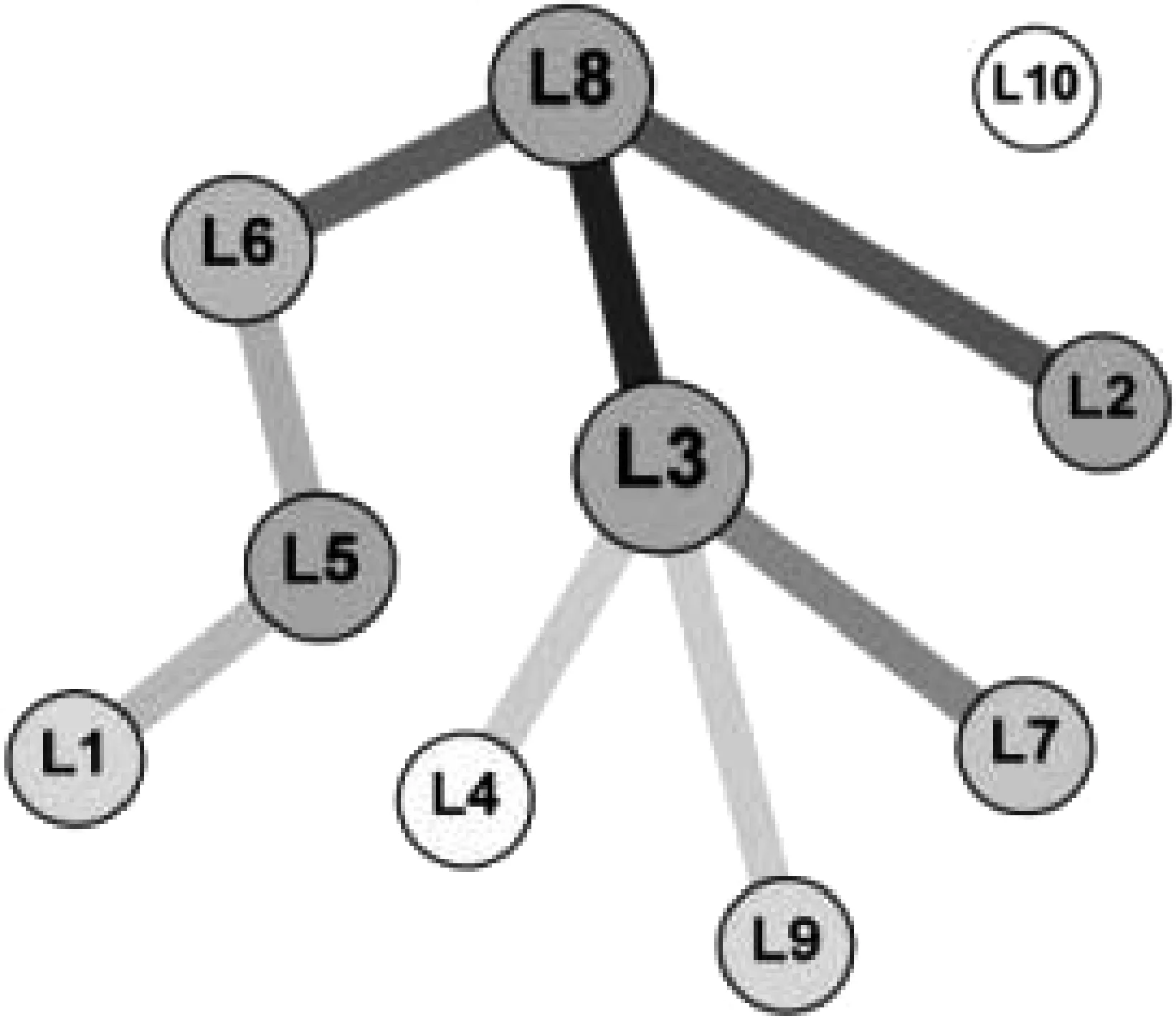
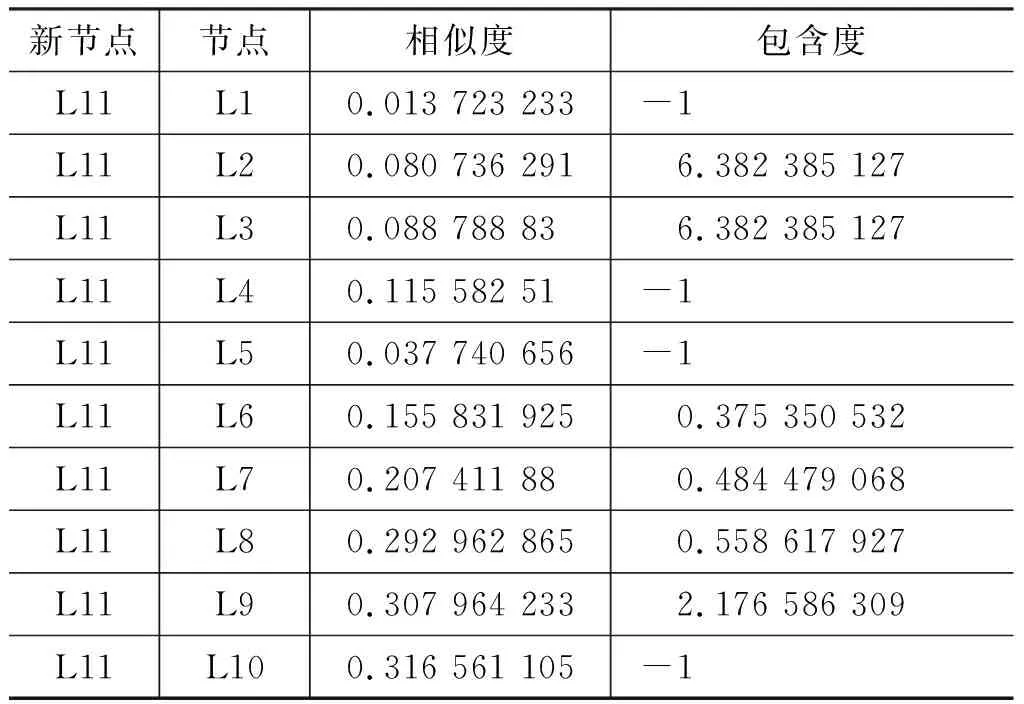
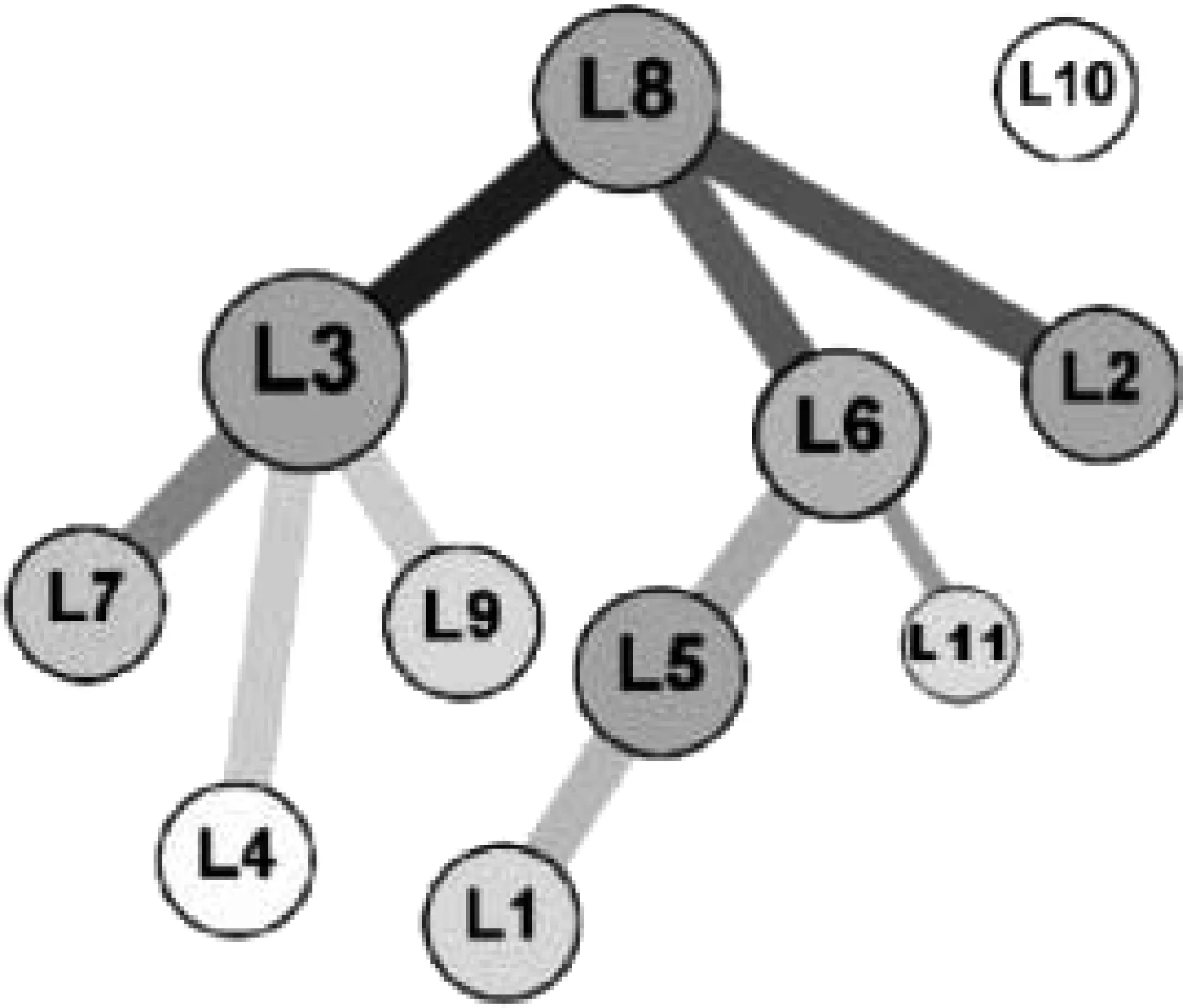
定义6(相异度) 对于政策个体L1和L2,设L1与L2之间的相似度为Sim(L1,L2),L1的子集SubL1与L2的子集SubL2形成以两政策节点之间的二元关系为元素的集合,S={ (3) L2相对于L1的相异度与上述公式类似。由上述定义可知,政策个体之间的相异度反映的是政策个体的个性程度。Dif(L1,L2)越大,说明在政策个体L1中,其包含的政策细胞与L2中政策细胞相异的就越多,政策个体L1相对于L2的个性程 度 就 越 大。那么对于政策个体L1和L2,在推断他们之间的包含关系时,假设相异度阈值β是一个较小的常数,则由相异度可以得到如下推断: (1) 若min{Dif(L1,L2),Dif(L2,L1)}>β,则说明,L1和L2不具有父子关系; (2)若Dif(L1,L2)>β>Dif(L2,L1),则L2是L1的子政策; (3)反之,若Dif(L2,L1)>β>Dif(L1,L2),则L1是L2的子政策;(4)若min{Dif(L1,L2),Dif(L2,L1)}≤β,则L1和L2是完全相同的两个节点; 定义7(政策个体之间的包含度) 对于政策个体L1对L2的包容度定义为政策个体L2从属于政策个体L1,其计算如式(4)所示。 (4) 由式(4)可知,当C(L1,L2) >1时,说明L2是L1的子政策;当C(L1,L2)∈(0,1)时,说明L1是L2的子政策。当C(L1,L2)=0时,说明L2与L1互为冗余政策;而当C(L1,L2)=-1时,说明L1与L2之间无父子关系。 对于已构建好的政策血缘网络,首选在宏观政策血缘网络LNet中选取度最低(即度为1)的n个节点SubLNet0={L1,L2,…,Ln}作为最底层的叶子节点(网络中度数最小的节点必定为叶子节点)。关于∀Li∈SubLNet0,其只存在一个邻居节点,设为pLi。假设网络是连通图的前提下,那么其邻居节点pLi必定会有另外的 邻 居 节 点。 故pLi的 度 一 定大于1,且其邻居节点pLi为Li的父节点。由此网络中初始形成了n个由SubLNet中节点以及其邻居节点形成类。之后,对于SubLNet中所有节点的邻居节点形成的集合NebSubLNet0,对∀Li∈NebSubLNet0满足Li没有父节点。首先,确定其邻居节点集合Neb={LiN1,LiN2,…,LiNm},然后,对于∀LiNj∈NebLi且满足Sim(Li,LiNj)以及LiNj没有父节点和子节点,分别计算C(Li,LiNj),根据包含度确定这Li和LiNj之间的父子关系。反复迭代,直至网络中最后一个节点的位置确定。算法的示意图如图6所示。 图6 PBNAP算法流程示意图 综上所述,政策血缘网络层次划分算法描述如下: 算法2 政策血缘网络层次划分算法输入: 政策血缘网络体系PNS,包含度阈值β输出: 宏观层次的政策血缘网络Lnet中的父子关系集合Rfor节点Li in Lnet{ for节点Lj in Lnet{ 计算Li与Lj之间的包含度C(Li, Lj) IfC(Li, Lj) > 0 && C(Li, Lj) < 1 { R=R∪{(Lj, Li)} }else if C(Li, Lj) > 1{ R=R∪{(Li, Lj)} }else if C(Li, Lj)=0{ R=R∪{(Li, Lj)} } } } 通过3.1节介绍的理论,实现了扁平化宏观政策血缘网络的树状层次划分。然而这种树状层次的形成是以牺牲政策个体内部比重较小的政策细胞之间的相似度为代价的。在实际的政策网络中,政策碎片化的正向传播体现在政策个体之间时,不仅没有鲜明的体系层次,且从政策文本内容上来讲,还存在着不同政策个体所包含的政策细胞之间的交叉。针对此问题,本文在层次化宏观政策血缘网络的基础上,对中观的政策细胞网络进行演化,消减网络中的碎片化节点。 在物理学中的万有引力定律中,任意两个质点通过连心线方向上的力相互吸引。该引力大小与它们质量的乘积成正比,与它们距离的平方成反比,与两物体的化学组成和其间介质种类无关。故可以如下定义政策个体之间的吸引力。 定义8(政策个体之间吸引力) 政策个体之间吸引力表示文本之间的相互吸引程度,它与文本的长度成正比,与文本之间的距离成反比。 对于政策个体L1={M11,M12,…,M1n}和L2={M21,M22,…,M2n},由上文可以计算L1,L2之间的相似度Sim(L1,L2),则文本之间的距离为: (5) 那么L1,L2之间的吸引力F(L1,L2)的计算公式为: (6) 对于政策文本L1和L2,它们所包含的内容越多,相似度越大,则它们之间的吸引力越强。对于一个政策细胞M和一个政策个体L,在考量它们之间的吸引力F(L,M)时可以将政策细胞M看成是一篇只由一条政策条款组成的政策个体,表示为长度为1的空间向量,那么它们之间吸引力可简化为式(7): F(L,M)=|L|×Sim(L,M) (7) 由此本文提出基于政策文本吸引力的政策文本去碎片化方法,其中政策森林的构建过程如图7所示。 图7 政策森林构建 具体的去碎片化算法描述如下: 算法3 政策血缘网络层去碎片化算法输入: 政策血缘网络体系PNS,Lnet的层次结构R(节点父子关系),相似度阈值γ输出: 政策血缘森林for Li in Lnet { for Lj in Lnet { if ( Li, Lj ) 不属于R { for Mx属于Li { 续表 通过政策血缘网络的去碎片化,删除了层次政策血缘网络中的非父子关系,从而构建了有一棵或多棵政策血缘树构成的政策血缘森林。下面对政策血缘树进行形式化定义: 定义9(政策血缘树)T(V,E, root(T))为一棵由政策文本组成的树,满足: (1)该树中,有且只有一个根节点root(T); (2)顶点集合V={L1,L2,…,Ln}中元素为政策文本; (3)边集合E={ek= 经过前面的介绍,已经可以将现存的碎片化政策进行层次构建,并消除了层次化血缘网络体系中的碎片化条款,从而形成政策血缘森林。在新政策制定的过程当中,政策制定者难以掌握所有现存政策信息,因此产生新的政策碎片。如何利用上面提出的层次化的政策血缘网络对新政策进行定位至关重要。本文提出一种基于树的层次检索的方法。对于新政策,在政策血缘森林中寻找与新政策节点相似的已存在的政策个体,通过与这些节点的匹配为政策制定者提供政策定位的辅助信息。 3.3.1 政策血缘网络层次有序化 层次化的政策血缘网络的实质是一棵或多棵政策血缘树组成的政策森林。每棵政策树中的父子节点之间的关系存在着相似度大,及包含度大的特点。这棵政策血缘树的兄弟节点对于父节点来说是平等的。它们所处的位置与它们与父节点的联系紧密程度无关,这不利于政策的逐层检索。因此,本文在前文所构建的政策血缘树的基础上,提出一种政策文本包含度的无序政策树有序化算法,其流程如图8所示。 图8 政策树有序化示例 对于图中政策血缘树T={L1,L2,…,L11},按广度优先的顺序对T进行层次遍历,对于遍历中的每个非叶子节点Li,设其直系子节点集合为Child(Li)=={Li1,Li2,…,Lin},对于∀Lij∈Child(Li),由加权树的边的权值可以得到Li对其子节点Lij的包含度C(Li,Lij),对Li的所有子节点按照包含度的由大到小进行排序,分别作为Li由左到右的孩子节点。继续迭代,直至政策血缘树T中所有的非叶节点的子节点全部有序排列。 3.3.2 新政策的位置锁定 应用上文构建的政策血缘有序树所构成的政策血缘森林,对于新制定的政策,本文提出一种基于有序树检索的政策碎片预防机制。该机制可以执行在新政策的制定和修订的过程中,用于检验新政策相对于已存在的政策树的冗余度,及对于非冗余政策在政策森林中插入位置的确定。其大致流程如图9所示。 图9 新政策的插入 如图9所示,对于一个新制定的政策Lnew,首先计算政策森林F={T1,T2,…,Tn}中所有树根节点对于Lnew的包含度Croot(F,Lnew),其中Croot(F,Lnew)包含的内容为Croot(F,Lnew)={C(root(T1Lnew)),C(root(T2Lnew)),…,C(root(TnLnew))}。Croot(F,Lnew)中,如果其最大元素Max(C(root(TnLnew)))<0,则将政策Lnew作为政策森 林F的 新 政 策树;若存在Lnew对某个跟节点的包含度大于所有根节点对于Lnew的包含度,则Lnew为该根节点的父节点;否则Lnew的从属于对于Lnew包含度最大的政策树,下面从该树的根节点开始,迭代计算Lnew与本次迭代的父节点的子节点中,寻找Lnew的下次迭代父节点,直到找到Lnew的直系父节点。寻找的过程如图10所示。 图10 新政策判余与位置锁定 图10中,已知本层父节点为L,本层父节点对新政策Lnew的包含度为C(L,Lnew),则在判断下一层节点时会遇到三种情况: (1)C(L,Lnew) >C(L,LLC),其中LLC为L的最左孩子。此时若Sim(LLC,Lnew) (2)C(L,Lnew) >C(L,LRC),其中LRC为L的最右孩子。此时若Sim(LRC,Lnew) (3)C(L,LCi) 具体的位置锁定算法描述如下: 算法4 新政策节点的插入位置锁定输入: 政策个体Lnew,有序化政策血缘森林F输出: 经过插入操作的政策森林F计算Lnew与F中所有根节点的包含度if max ( C( Lnew, root(T) ) )=0{ Lnew 为冗余政策}else if max ( C( Lnew, root(T) ) ) > 1{ Lnew 为政策血缘树的新的根节点}else if max ( C( Lnew, root(T) ) ) < 0{ Lnew 为政策森林中的一棵新树}else{ Lnew 为树T的子节点, 按包含度确定Lnew邻居兄弟节点 if存在包含关系, 则遍历下一层 else{ 在兄弟节点之间插入Lnew }} 本实验以中华人民共和国人力资源与社会保障部网站上,政府公开法律法规的养老保险菜单中,城镇职工基本养老保险目录下的10个养老保险相关政策文本为例,验证文中研究技术的有效性。实验中使用的每一个政策文本,均保存为txt格式。实验分为四个阶段,分别为: (1) 政策文本相似度计算。通过依存句法分析方法,基于《知网》的词语相似度计算方法,政策细胞相似度计算方法,以及政策个体相似度计算方法,实现政策文本相似度计算。 (2) 依据政策文本相似度计算结果,构建城镇职工养老保险政策血缘网络体系。探究各层次城镇职工养老保险政策血缘网络特点。 (3) 在政策血缘网络体系的基础上,对宏观政策网络进行层次划分,去碎片演化,观察树状政策血缘网络结构特征。 (4) 在政策血缘森林的基础上,分别对一个新政策个体及数据集中某政策个体的部分政策细胞稍加改动作为“新政策”,对新政策的冗余判断及位置锁定仿真。在此,本文仅展现重要步骤的实验结果,省略了某些中间过程的结果。 经过了政策基因、政策细胞和政策个体之间的相似度计算之后,可以分别构建微观政策血缘网络、中观政策血缘网络和宏观政策血缘网络。其中,微观政策网络共14 885个节点,中观政策血缘网络节点共644个,宏观政策网络节点共10个。三层网络构建结果分别如图11~13所示。 图11 微观政策血缘网络 由图11中,随着节点度的由小增大,节点的颜色由深至浅逐渐变化。而边的颜色由深至浅是由边的权重(节点相似度)由大变小导致的。由微观层次的政策网络图可以看出,微观层次的网络节点度分布满足无标度特性。 图12为中观层次的政策血缘网络。由图可知: 中观层次的政策网络节点的度分布也明显具有无标度的特性。该图中节点越大,颜色越深,度越大;边颜色越深权值越大。图12可以较为明显的看出实验数据及中的不同政策文本间,第五条政策细胞的相似度比较大。 图12 中观政策血缘网络 由图12可以看出,政策L1、L2、L3、L4、L5、L6、L7、L8、L9的第5个条款M5相似度较大,且与其他同一政策文本内的其他政策细胞基本不相似,由此可以推断该条款为政策文本中的通用性文字,与特定政策相关性不大。而对于图中类似于L8M1、L6M4等节点,其度较大。说明与其相似的政策细胞较多,从而可以推断该条款包含内容较广,后续有可能细化成多个政策细胞或者独立的政策。 图13为宏观政策血缘网络的网络图,由图可知,政策文本L8、L5、L2与较多的政策之间存在着相似关系,因此可能成为政策树的根节点。而L5与L4、L3与L8、L8与L2之间存在着较强的相似关系,因此有可能成为具有父子关系的节点。 图13 宏观政策血缘网络 4.2.1 政策血缘网络的层次划分 对于构建好的宏观政策血缘网络,仅仅能感性的从中观察出可能的节点间关系。而且该政策网络是扁平的,并不存在明显的层次结构。针对此问题,本阶段主要对上一阶段构建的宏观层次的政策网络进行层次划分、政策树的构建等相关处理,以提取出宏观层次的政策血缘网络中的层次结构。首先,要对宏观政策血缘网络中的层次结构进行提取。本实验中,相异度阈值β选定为0.896,各政策个体之间的包含度计算部分结果见表2。 表2 政策个体包含度计算部分结果 经试验反复调试,本实验采用包含度阈值c为0.3,则政策个体中,包含度大于3或大于0小于0.3的为存在父子关系的节点,则由政策个体之间的包含度,将宏观层次的政策网络进行层级划分,结果如图14所示。 图14 宏观政策血缘网络层级划分 图14中,节点间较宽的边即为有政策节点之间的包含度所提取出的父子关系,节点之间的边颜色越深,则该边两段所连接的父子节点中,父节点对于子节点的包含度越大。而包含所述内容较多的节点,其包含的子节点越多。如图中节点L8的直系孩子节点为L2,L3,L6,而节点L6的直系孩子节点只有L5,那么由此可以初步推断,L8比L6包含更多的政策信息。 4.2.2 政策血缘网络的去碎片化演化 层次化的政策血缘网络中还存在着很多相似度较大的非父-子关系的节点。针对这样的节点,分析其内部相似度较大的政策细胞,并计算这种条款与对应节点之间的万有引力。对于层次化的宏观政策血缘网络中的非父子节点,分别检索这些非父子节点内部条款见的相似度。当相似度大于阈值γ大于0.5时,则对该政策细胞与对方政策个体的万有引力进行计算。并将该政策细胞划分到万有引力较大的政策个体中,经过去碎片化演化的政策血缘网络形成政策血缘森林。如图15所示。 由图15可知,由实验数据集中这10个政策文本组成的宏观政策血缘网络经过去碎片化演化形成的政策血缘森林为两棵政策血缘树。其中一棵树只有一个根节点L10,另一棵树中包含9个政策个体,L8为根节点。对于树中的父子节点,其对于子节点的包含度越大,边的颜色越深。对于一个根节点,其子节点的个数越多,意味着该节点越有可能包含更多的信息。而对于一对指定的父子节点,其包含度越大,说明父节点与子节点父子关系的可靠性就越大。 图15 政策血缘森林 4.2.3 政策血缘森林的有序化 上面所构建的政策血缘森林中的政策血缘树是无序树。即对父节点来说,其与某个子节点间包含关系的大小与该节点位置无关,这种无序状态不利于树的检索与插入操作。因此,本实验对上述政策血缘森林进行包含度的排序,得到有序化的政策血缘森林,其过程如图16所示。 图16 政策血缘有序森林 图16中,在经过有序化的政策森里共包含两棵政策有序树,其根节点分别为L8和L10,其中L10为只有一个节点构成的政策树。而在以L8为根节点的政策有序树中,随着父子节点间边的由深至浅,所有父节点的子节点均按照父节点对其包含度由大到小排列。 4.2.4 新政策位置锁定 对于上述有序化的政策血缘森林,假设有L11为新政策节点,本文将演示该政策在政策血缘森林中进行亲缘关系寻找与位置锁定的过程。该过程通过计算原有政策森林中的各节点对于新的政策节点的包含度,进而判断原有政策节点与新政策节点之间的潜在父子关系。首先计算该节点与政策森林中所有节点之间的包含度和相似度,计算结果见表3。 表3 新政策与政策血缘森林节点之间的相似度与包含度 图17 新节点的插入 图17中,经过包含度和相似度的计算,新政策L11为非冗余节点,且是政策L6的左孩子。图中节点的大小表示节点孩子数目的多少,而边的粗细表示父子节点间包含关系的强弱。 本文提出一种自动化的政策系统结构分析方法,通过分析政策之间深层联系,实现碎片化政策的网络结构组织,并进行碎片消解,形成结构清晰的政策网络,实现基于该政策网络的新政策碎片预防。本文提出的政策分析与制定计算机辅助技术,可以帮助决策者直观地把握政策的体系结构,预测新政策在该政策体系中的地位,为有效地消减和预防政策碎片化现象提供了有效的解决方案。目前,本文提出的方法尚未完全成熟。如政策文本相似度计算算法,仍处于牺牲算法效率换取算法精确度的阶段,尚不足以处理大规模的文本集。未来的工作主要集中在此类算法的性能优化上,以充分发挥本政策血缘网络体系及演化方法在现实政策分析中的重要作用。 [1] 冯莹. 碎片与重塑社保制度公平之路[N]. 人民法院报,2010-05-17. [2] 朱亚鹏.公共政策研究的政策网络分析视角[J].中山大学学报, 2008: 80-83. [3] Ismael Blanco, Vivien Lowndes, Lawrence Pratchett. Policy Networks and Governance Networks: Towards Greater Conceptual Clarity[J]. Political Studies Review, 2011: 25. [4] 杨代福.政策网络理论途径的缺失与修正.理论月刊, 2008(3):82-85. [5] 谭羚雁, 娄成武. 保障性住房政策过程的中央与地方政府关系——政策网络理论的分析与应用[J]. 公共管理学报, 2012, 09(1):52-63. [6] 朱春奎.政策网络与政策工具:理论基础与中国实践[M].上海:复旦大学出版, 2012. [7] 唐云锋, 许少鹏. 政策网络理论及其对我国政策过程的启示[J]. 中共浙江省委党校学报, 2012, 28(2):40-45. [8] 范如国.制度演化及其复杂性理论[M]. 北京: 科学出版社, 2011. [9] 刘刚.面向领域的软件需求一致性验证方法研究[D]. 哈尔滨工程大学博士学位论文, 2008:21-54. [10] 刘影. 面向领域的隐形政策血缘挖掘方法研究[D]. 哈尔滨工程大学硕士学位论文, 2013:14-33. [11] 路彩霞. 基于语义的领域政策要点分析与形式化方法研究[D].哈尔滨工程大学硕士学位论文, 2014:8-46. [12] 卢志刚,刘俊荣,刘宝旭. 基于GTST-MLD的复杂网络风险评估方法[J]. 计算机科学, 2014.14-23. [13] 陈宝楼. K-Means算法研究及在文本聚类中的应用[D]. 安徽大学硕士学位论文, 2013.23-46. [14] 张瑞霞, 杨国增, 吴慧欣. 基于《知网》的汉语未登录词语义相似度计算[J]. 中文信息学报, 2012, 26(1):16-21. [15] 朱新华, 马润聪, 孙柳,等. 基于知网与词林的词语语义相似度计算[J]. 中文信息学报, 2016, 30(4):29-36. [16] 陈功,罗森林,陈开江,等.结合结构下文及词汇信息的汉语句法分析方法[J]. 中文信息学报, 2012(1): 9-15. [17] Calvo H, Gambino O J, Gelbukh A, et al. Dependency syntax analysis using grammar induction and a lexical categories precedence system[C]//Proceedings of the Computational Linguistics and Intelligent Text Processing -, International Conference, Cicling 2011, Tokyo, Japan, February 20-26, 2011. Proceedings. DBLP, 2011:109-120. [18] 车万翔,张梅山,刘挺.基于主动学习的中文依存句法分析[J].中文信息学报, 2012(2):18-22. [19] 辛霄,范士喜,王轩,等.基于最大熵的依存句法分析[J].中文信息学报, 2009(2):18-22. [20] 黎琛. 基于依存树相似度计算的汉语复句关系词自动识别[D]. 华中师范大学硕士学位论文, 2015. [21] Abril D, Navarroarribas G, Torra V. Vector Space Model Anonymization[J]. 2013, 256:141-150.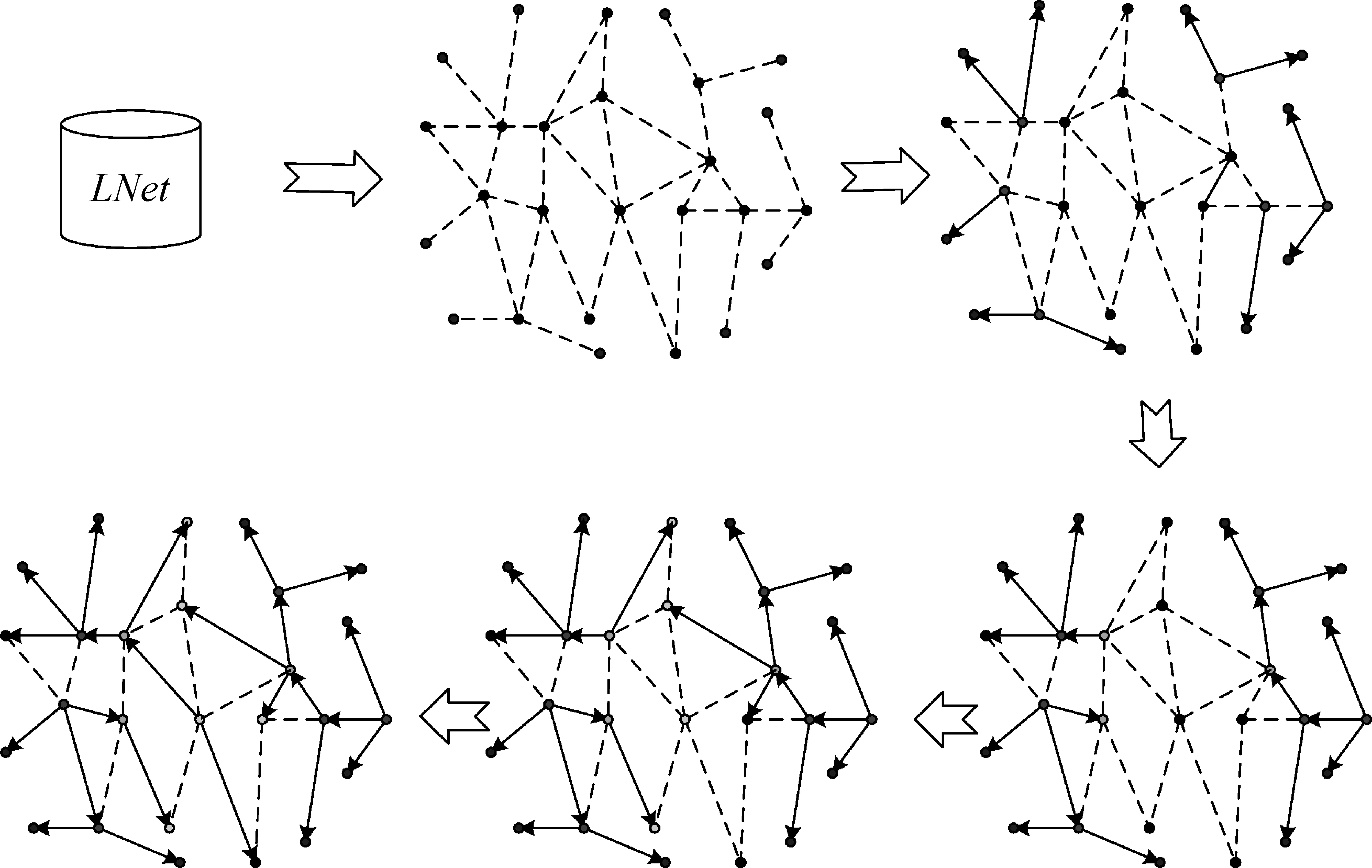

3.2 政策网络的去碎片化演化



3.3 政策碎片化的预防


4 实验结果及分析
4.1 隐性血缘政策网络体系的构建


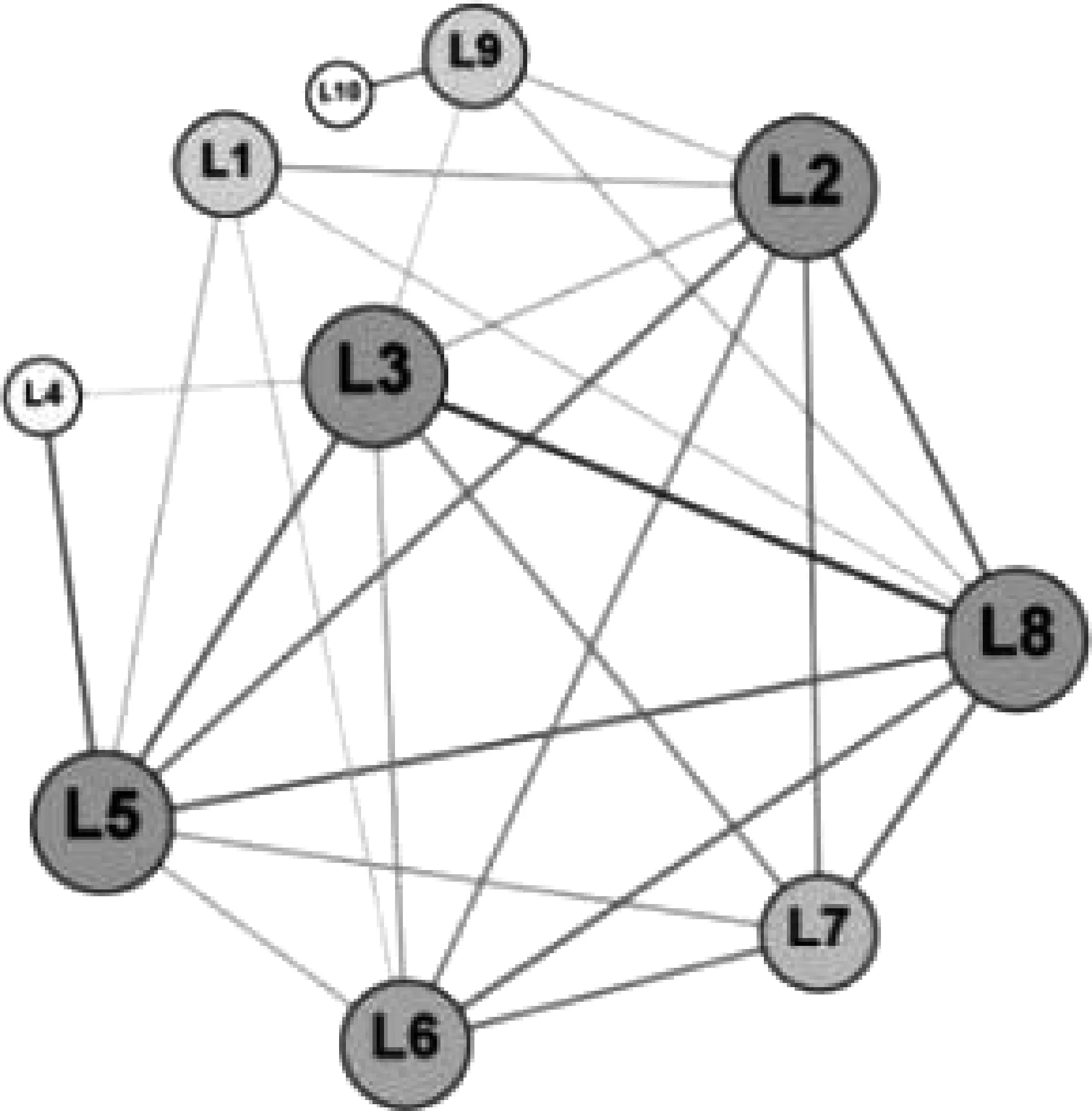
4.2 政策血缘网络的结构演化



5 结论

