基于灰色系统理论在车辆工程的应用探究

胡浩

（西安科技大学，陕西 西安 710600）

纵观客观世界中的实际问题，其内部的某些结构、特征参数并未全部被人们所了解，人们不可能像研究表面现象问题那样将其内部的结构机理研究清楚，只能依据某些逻辑思维和一些特殊的方法去推断进行构造模型，通常我们称之为灰色系统。在车辆工程应用方面，我们同样对其内在的一些结构、特征参数了解得并不透彻，那么我们就需要通过灰色系统理论建立模型去进行探讨研究，以便更好的应用于人类生活的方方面面，去解决和分析实际问题。

1 概述

1.1 灰色系统理论得产生背景

人类在历史的发展、社会、经济活动以及科学研究过程中，经常会遇到一些信息和条件不足的情况。比如在农业生产中，即使是播种面积、种子、化肥、灌溉条件等信息完全明确，但是由于劳动力的技术水平、气候条件、市场行情等信息不明确，仍然难以准确地预计出产量、产值。这些问题的出现就促使了人们研究各种不确定性问题的理论，随之适用方法也就逐步产生了。

随着科学技术的发展、人类社会的进步以及城市化进程的加速，人们对各类系统的不确定性有了初步认识，随之不确定性系统的研究也日益开拓。在20世纪后半叶，在科学研究过程中，越来越多的不确定性问题的出现，推进了各种不确定性系统理论和方法的出现和发展。扎德教授于20世纪60年代创立了模糊数学，邓聚龙教授于80年代创立了灰色系统理论，帕拉克教授于80年代创立的粗糙集理论和王光远教授于90年代创立的未确知数学等，这些都是不确定性问题研究的重要成果。这些方法从不同角度、不同方向阐述了研究和处理各类不确定性问题的理论和方法。

1.2 灰色系统理论的概念

灰色系统理论是在20世纪80年代提出的一种新的处理不确定性问题的有力研究方法。灰色系统理论是以小部分已知信息或条件的小样本不确定性问题为研究对象，主要通过对问题中部分条件提取有价值的信息，对整个不确定性系统做出一定的监控，最终得出比较准确的结论，以便应用在实际生活中。灰色系统理论以给定的条件为基础，通过对问题的分析认证，建立一定的模型，求取问题的最佳答案，较适用于思维的综合和判断。

灰色系统理论中的“灰”可以有诸多解释，见表1。

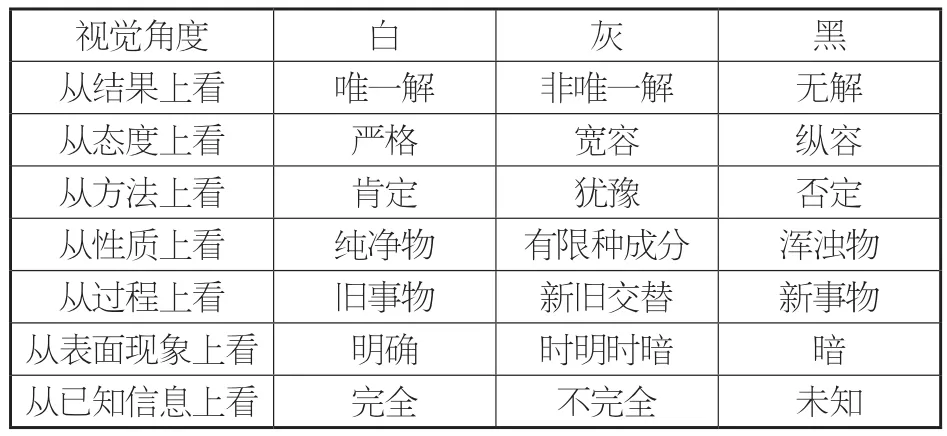
表1

1.3 灰色系统理论的发展趋势

在上文简单论述了灰色系统理论产生的背景及其基本概念，随着科技的进步，城市化进程的加快，日常生活中暴露出的问题也逐步增加，使得人们对灰色系统理论的研究进入了一个空前的高度，推进了灰色系统理论的发展。目前灰色系统理论成功应用到了诸多领域，如工业、车辆工程、交通、环境、医学和教育等。灰色系统理论得到广泛应用，成功的解决了日常生活生产和研究中大量的实际问题。

灰色系统理论以其庞大的生命力不断发展，逐步完善，奠定了其在学术界的地位，发展前景备受国内外学者以及研究人员所重视。

2 车辆工程

2.1 车辆工程概述

车辆工程是一门研究车辆动力学与各种机动车等机械制造的理论以及技术和发展方向的工程方面的学科。它主要包括机动车辆以及交通运输工具的理论设计、研究开发、生产制造和质量检测等关键技术。

车辆工程经过几千年的发展演变，从最初研究的材料力学、机械设计与加工、流体力学等,到今天广泛应用到人类生活的方方面面，形成了诸多领域，是一门技术与综合性很强的学科。

2.2 车辆工程的发展

随着科学技术的进步，我国在机动车辆方面的发展逐步赶上了国际的发展步伐，在产品技术和质量方面，与国际最先进的技术水平的差距已经逐步缩小，达到了一个很高的地步。现在一些新型合成的复合材料已经逐步应用到车辆工程领域之中，解决了一些问题，同时给人们的生活带来了诸多便利。此外，在车辆工程上，自动化已经成为了发展主流，如在汽车上应用了自动挡等。

随着“互联网+”时代的到来，在车辆工程中也掀起了“互联网+汽车”的潮流。随着技术的不断发展，科研人员不断突破一个个难题，相信在不久的将来，机动车辆完全能够实现全自动化操作。

纵观车辆工程领域近年来的发展，车辆制造业发展的趋势和方向势必沿着绿色、环保以及自动化方面发展，积极响应“十三五”的环保理念，切实贯彻创新、协调、绿色、智能的发展理念，努力完成“十三五”的目标。

3 灰色系统理论应用到车辆工程

在现阶段灰色系统理论的应用，大多在于汽车运行以及交通的车辆工程领域中。通常针对不确定性问题，先进行灰色预测，再建立模型，列出相应的微分方程，运用数学的知识进行求解，进而解决实际问题。

为了取得可靠的理论依据，研究人员对车辆工程中的常规的公交客运进行分析论证。对此进行研究有以下几点依据：（1）随着城市化进程的加快，机动车辆的快速增长，导致了道路交通拥挤、阻塞等问题。（2）公共交通成为居民出行的重要交通工具。（3）公共交通符合可持续发展的理念，积极响应“十三五”精神。

在对公共交通线路这个不确定性问题用灰色预测模型来研究，采用了传统灰色预测模型和常规方法的预测这两种方法进行研究分析对比，得出更精准的数据。

目前常规方法的预测常用的是多元线性回归模型、平均增长系数模型和组合预测模型等。

而通过研究分析对比，研究人员发现传统的灰色预测模型更加优于常规方法的预测，精准度更高。

灰色预测分析过程通常包括灰色的生成、求参运算以及精度检验这3个步骤。

灰色的生成即GM模型的建立，列出相应的微分方程，如，其中Xi为n个观察值，α，β为待测参数。

求参运算：通过最小二乘法求解α，β；再通过求解矩阵得出观察值Xi的通解。

精度检验即残差检验。利用残差建立一个修正模型，可以消除误差，提高精度。

4 结语

迄今为止，国内学者研究的主要方向仍然是灰色系统理论，为灰色理论作出了极为重要的贡献。在灰色预测中，通过构建灰色模型建立微分方程组，可以有效的处理一些不完整以及零乱的数据，在一定程度内具有良好的实用性，对交通的预测有很好的应用价值。灰色系统理论通常对小样本数据及问题进行预测，这促使灰色系统理论在很多工程实践中大量应用，同时也取得了比较满意的预测结果。

[1]袁嘉祖．灰色系统理论及其应用[M]．科学出版社,1991．

[2]刘思峰、郭天榜、党耀国等．灰色系统理论及其应用[M]．北京：科学出版社，1999．

[3]肖新平，毛树华．灰预测与决策方法[M]．北京：科学出版社，2013．

[4]邓志龙，李全，陈茜．基于灰色系统理论的短时交通流预测[J]．公路交通技术，2006．

[5]罗党，王洁芳．灰色决策理论与方法[M]．北京：科学技术出版社，2012．

[6]张爱霞，张云鹏．客运交通量预测模型构建与分析[J]．河北理工大学学报：自然科学版，2010．