基于Lyapunov函数的NPC型三电平SAPF非线性控制策略

程启明, 李 涛, 张 宇, 程尹曼, 谭冯忍, 高 杰

(1. 上海电力学院自动化工程学院, 上海市 200090; 2. 上海市电站自动化技术重点实验室, 上海市 200090;3. 同济大学电子与信息工程学院, 上海市 201804)

0 引言

近年来,整流、变频装置的广泛使用和半导体非线性负荷的快速增加,使得电力系统面临着越来越严重的谐波污染问题[1]。采用并联型有源滤波器(shunt active power filter,SAPF)对电网的谐波进行动态实时补偿,已成为最有效、最具前景的途径之一[2]。

三电平SAPF相比于传统的两电平SAPF有许多优点,例如具有较低的开关频率和损耗,耐压,在较高电压系统中获得了应用等[3]。三电平SAPF的拓扑结构主要有中性点钳位(neutral-point clamped,NPC)型、飞跨电容型和级联H桥型[4],其中NPC型所需的直流侧电容数量和所需解决的直流侧电压不平衡问题最少、鲁棒性最好[5]。目前,国内外的研究大多是基于三相三线制以及单相半桥系统,而对于三相四线制系统的研究则较为有限[6]。但三相四线制系统增加了对零序分量的处理,不仅能对三相平衡系统的谐波和无功功率进行补偿,而且能对电网不平衡时非线性负荷产生的零序谐波分量进行补偿[7],因此本文选择三相四线制NPC型三电平SAPF作为研究对象。

NPC型三电平拓扑结构虽具有许多突出的优点,但中点电压不平衡也是其固有的缺陷[8]。中点电压波动会降低系统的稳定性,严重时甚至会使系统无法正常工作,因此必须对其进行控制。通过调节空间矢量脉宽调制(space vector pulse width modulation,SVPWM)算法中的正负小矢量的作用时间即可实现中点电压平衡控制[9]。由于一对冗余小矢量对直流侧中点电位的影响是互补的,因此,本文采用基于电荷平衡原理的控制方法,通过引入平衡因子f调节一对冗余小矢量的作用时间来实现对中点电位的实时控制。

稳定有效的控制器设计是SAPF理论研究的关键所在。传统的控制策略主要依据局部线性化方法,当系统参数或负载发生变化时,控制性能不稳定,且由于SAPF的动态方程是非线性的,因此对SAPF的控制效果不佳[10]。近20年来迅速发展的非线性控制系统的微分几何理论为这一问题提供了可行的解决方案。文献[11]提出利用状态反馈精确线性化方法建立其线性化模型,可实现对SAPF三相进行解耦控制,但该方法需建立精确的系统模型;文献[12]提出滑模控制方法,该控制策略虽能取得较好的补偿效果,但其存在高频抖动的问题;文献[13]提出基于无源理论的自适应滑模控制,能实现谐波电流和直流侧电压的快速跟踪控制,但只能实现平衡负荷下的控制。文献[14]将基于Lyapunov函数的非线性控制方法引入SAPF中,可实现负载变化时的实时控制,但控制对象为小功率的单相SAPF。

为此,本文提出了NPC型三电平SAPF的新型控制方法——基于Lyapunov函数的非线性控制策略。该方法从能量角度出发,设计电流内环采用基于Lyapunov函数的稳定控制器,并以增强系统抗干扰性为目标,求取控制器最优增益,确保线路参数或负载发生变化时,系统仍能稳定运行;电压外环采用传统的比例—积分(PI)控制,保证直流侧电压的稳定,实现非线性负载突变时的动态调节。仿真和实验结果均能证明本文提出的基于Lyapunov函数的非线性控制策略用于电网平衡/不平衡下NPC型三电平SAPF的有效性和可行性。

1 三相四线制NPC型三电平SAPF的结构及建模

本文研究的三相四线制NPC型三电平SAPF电路结构如图1所示,它由电网电源、非线性负载和NPC型三电平SAPF组成。

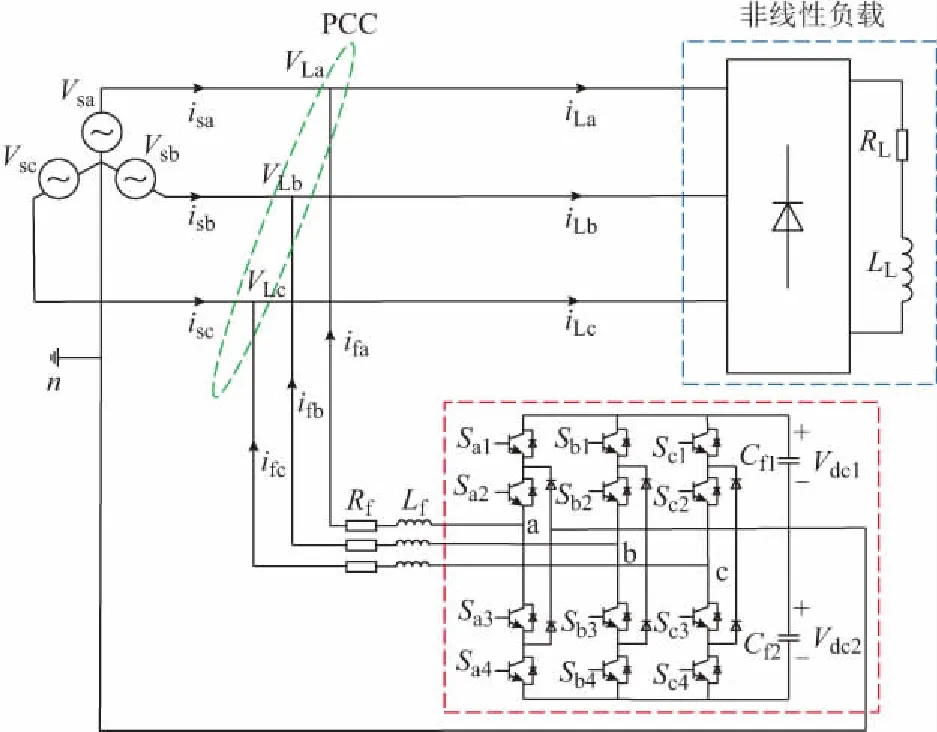
图1 三相四线制NPC型三电平SAPF的电路结构Fig.1 Circuit structure of NPC-type three-level SAPF for three-phase four-wire system

图1中,Vsi(i=a,b,c)和isi分别为电网三相电压和电流;VLi为公共连接点(PCC)处的三相电压;Vdc1和Vdc2分别为直流侧电容Cf1和Cf2的两端电压;iLi为三相负载电流;ifi为SAPF三相补偿电流;RL和LL分别为三相整流桥后串联的阻、感性负载;Sij(i=a,b,c;j=1,2,3,4)为三相四线制三电平SAPF的开关函数,其定义如下[15]:

(1)

由式(1)可得,当Si1=Si2=1,Si3=Si4=0时,SAPF输出侧相电压Vin=Vdc1;当Si1=Si2=0,Si3=Si4=1时,Vin=-Vdc2;当Si2或Si3=1,Si1=Si4=0时,Vin=0。

为了建立NPC型三电平SAPF的数学模型,假设:①半导体开关器件是理想开关;②三相的滤波电感Lf、滤波电阻Rf是对称的;③直流侧两个电容Cf1和Cf2相等,即Cf1=Cf2=Cf。根据基尔霍夫定律,可得其在abc三相静止坐标系下的周期平均数学模型为[16]:

(2)

根据坐标变换理论,采用等功率变换,由式(2)可得NPC型三电平SAPF在同步旋转dq0坐标系下的数学模型为:

(3)

式中:Skm(k=d,q,0;m=1,4),ifk,VLk分别为dq0坐标系下的开关函数、SAPF补偿电流、PCC处电压在dq0轴的分量;Cd为abc/dq坐标变换之后的直流侧分压电容;ω=2πf为电源角频率,其中f=50 Hz为电网频率。

2 三相四线制NPC型三电平SAPF的非线性Lyapunov控制器设计

2.1 NPC型三电平SAPF的稳态非线性数学模型

当系统工作在稳态时,SAPF输出电流和直流侧电压均为对应的参考值,即稳态时x=x*,则结合式(3)可得稳态时NPC型三电平SAPF的数学模型为:

(4)

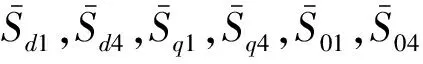
本文采用SVPWM策略,为保持开关函数的对称性,稳态开关函数选择为[17]:

(5)

结合式(4)可得稳态时dq0坐标系下开关函数的关系式为:

(6)

2.2 电流内环基于Lyapunov函数的控制器设计

令误差e=x-x*,结合式(3)和式(4)可得系统的误差动态特性方程为:

(7)

以系统全局渐进稳定为目标,结合Lyapunov理论,设计NPC型三电平SAPF系统的正定能量函数为:

(8)

式(8)满足初始条件的要求,即e=0时,H(e)=0;e≠0时,H(e)>0。

结合式(7),可得式(8)对时间的导数为:

(9)

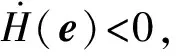
(10)

式中:α1,α2,α3<0分别为系统dq0轴上Lyapunov函数的控制增益。

由式(10)可知,电流内环Lyapunov控制器的设计只需合理地设计控制增益α1,α2,α3的取值,即可实现对控制目标的合理控制。虽然电流内环采用Lyapunov函数控制器存在一些变量,但是大部分变量都是已知的,无需复杂的设计。然而,对于传统的比例—积分—微分(PID)控制,不仅需要考虑比例参数、积分参数以及微分参数的影响,同时,线路参数的影响也至关重要;对于滑模与无源控制,控制器的设计比较复杂,涉及的变量参数比较多。采用Lyapunov函数控制器只需将控制目标转换为控制增益的设计,并将求解的开关函数结合SVPWM调制算法驱动变换器开关动作,避免了繁杂的坐标变换和公式计算。附录A图A1即为内环控制原理图。

2.3 Lyapunov函数的控制增益选取

为了研究不精确参考值的影响,假设[18]:

式中:η1,η2,η3为系统期望参数。

同时,由于外环电压响应速度远远大于内环[19],因此可假设Vdc1=Vdc2,即e5=e4,z5=z4,则不精确控制下的Lyapunov函数的导数(见式(9))变为:

(11)

(12)

式中:λ1为β1的二次函数。

当β1=(1+η1)/(2η1)时,λ1取得最小值,即

(13)

只有当λ1,min>0成立时,式(11)负定。λ1,min随η1的变化趋势如附录A图A2所示。为确保系统的渐进稳定性,设ηa<η1<ηb,其中ηa和ηb满足:

(14)

为确保线路参数变化时系统依然稳定,α1应尽可能小(μ1尽可能趋于0)。

对于期望参数的不确定区间η1∈[1-ε1,1+ε1],由式(15)求得|α1|的取值区间为:

(15)

式中:V′为直流侧电压实际值。

由式(15)可知,若不确定范围ε1取0.05,且Rf=0.4 Ω,V*=800 V时,|α1|的取值区间为[0,0.001 9]。同理可求得|α2|和|α3|的取值区间。

2.4 NPC型三电平拓扑结构的中点电压平衡控制

本文选用SVPWM作为NPC型SAPF的调制方法。通过分析可知,当参考矢量作用在Ⅰ扇区时,其中一个小矢量只对Cf1两端的电压Vdc1起作用。当ifa<0时,对Cf1进行充电;当ifa>0时,对Cf1进行放电。加入平衡因子f后,电容Cf1在一个控制周期Ts内的电荷变化量为:

(16)

另一小矢量只对Cf2两端的电压Vdc2起作用。同理可知,加入平衡因子f后,电容Cf2在Ts内的电荷变化量为:

(17)

设在一个Ts内,电容Cf1和Cf2的电荷分别为Q1=Cf1Vdc1,Q2=Cf2Vdc2,则由电容电荷的平衡条件[16]可知:

Q1+ΔQ1=Q2+ΔQ2

(18)

由此可得平衡因子f为:

(19)

同理可得当参考矢量分别作用在Ⅱ～Ⅵ扇区时,平衡因子f的表达式。

通过上面分析最终可得三相四线制NPC型三电平SAPF系统的控制框图,如图2所示。由图可见,电流内环采用基于Lyapunov函数的控制策略,可快速跟踪参考电流;直流侧电压外环采用PI控制,能使直流侧电压保持在设定值V*并获得较好的动态性能。

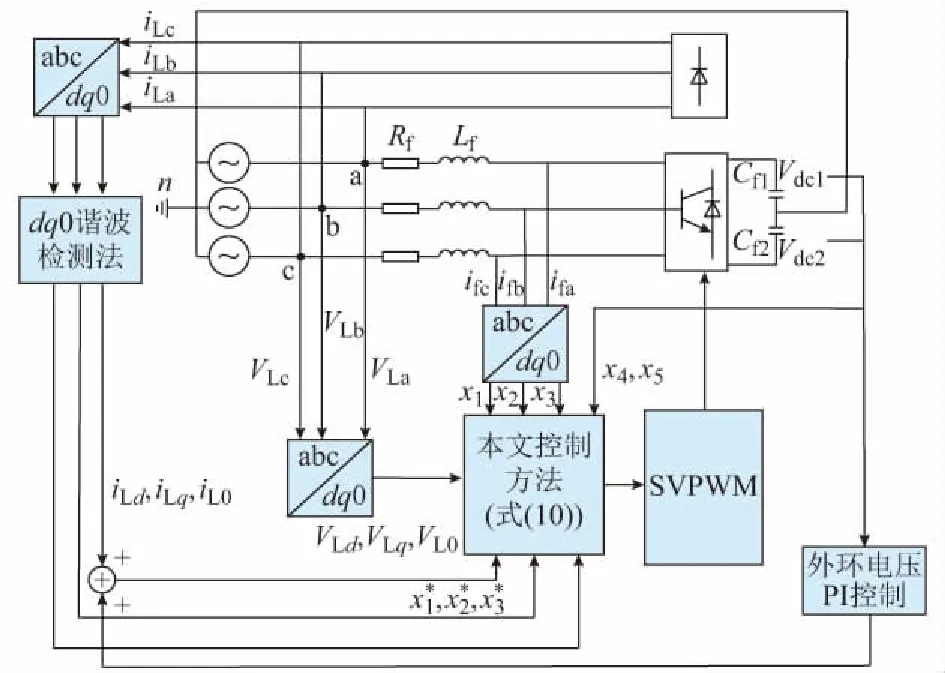
图2 三相四线制NPC型三电平SAPF的控制框图Fig.2 Control block diagram of NPC-type three-level SAPF for three-phase four-wire system

3 软件仿真分析

为了验证本文提出的基于Lyapunov函数的非线性控制策略的可行性和优越性,利用Simulink仿真软件对电网平衡/不平衡时,三相四线制NPC型三电平SAPF系统进行仿真研究,并将本文所提出的控制策略与传统PI控制策略进行仿真比较。

仿真参数取值为:三相电源为220 V/50 Hz;电网的阻抗Rs=0.2 Ω、感抗Ls=0.5 mH;负载的阻抗RL=30 Ω、感抗LL=10 mH;SAPF输出侧的滤波电感Lf=4 mH、滤波电阻Rf=0.4 Ω,直流侧电容Cf=5.5 mF,V*=800 V;Lyapunov函数的控制增益α1=α2=α3=-1.5×10-4;本文提出的方法下,电压外环KP=0.17,KI=0.02;传统PI控制方法下,电压外环KP=0.17,KI=0.02,电流内环KP=0.2,KI=0.5,仿真时间为0～0.42 s。

3.1 电网电压平衡时的控制性能分析

1)系统控制性能分析

在t=0.2 s时,接入另一相同的负载,达到稳态后,在t=0.3 s时又断开该负载。这一加载和卸载的过程会引起谐波电流成倍的变化,从而可以考察系统的动态跟踪能力。仿真结果如图3所示。

由图3可见,未补偿时(t=0～0.2 s),abc各相非线性负载电流非正弦且谐波含量较大,总谐波畸变率(total harmonic distortion,THD)分别为22.46%,22.58%,22.29%;经SAPF补偿后(t=0～0.2 s),电源电流正弦化,谐波含量大大降低,THD分别下降至2.47%,2.46%,2.52%;经电压外环控制后,直流侧的总电压能维持在800 V,且纹波较小;上、下电容两端电压差也能近似为0。在t=0.2 s加载时,负载电流突增一倍,约需0.03 s达到新的稳态;在t=0.3 s卸载后,也能快速达到新的稳态,验证了该系统具有良好的动静态特性。

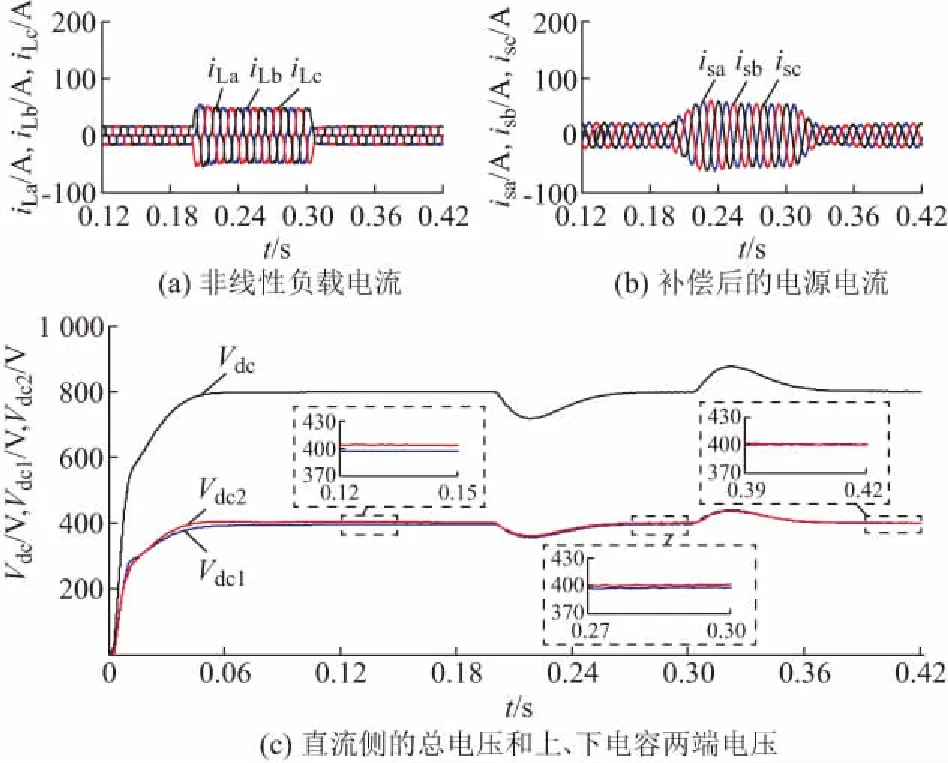
图3 电网三相电压平衡时的仿真曲线Fig.3 Simulation curves when three-phase voltage of the power grid is balanced

2)Lyapunov函数的控制增益α对SAPF补偿效果的影响

由式(16)可知,α值越小,稳定裕度越大,系统的动态性能和鲁棒性越强,但开关纹波会随之增加。下面分别在α=-0.000 15附近的[-0.000 13,-0.000 17]范围内选取不同的α值进行对比分析,THD和功率因数见表1。

表1 不同α值下SAPF的补偿效果Table 1 Compensation effect of SAPF for different values of α

由表1可知,α值越小,THD值越小,但当α<-0.000 15时,开关纹波增加,使THD值增大。因此本文选取THD值最小时对应的α值,即选取α=-0.000 15。

3.2 电网电压幅值不平衡时的控制性能分析

abc三相电源电压的有效值分别为220,150,192 V,此时电网电压的幅值不平衡,无加载和卸载过程。附录A图A3至图A5分别为SAPF补偿前、本文所提控制方法下的SAPF补偿后、传统PI控制方法下的SAPF补偿后的仿真曲线。

由附录A图A3可见,补偿前,三相电源电流非正弦且谐波含量较大,其中a相电源电流THD为23.59%。

对比附录A图A4(a)和图A5(a),经SAPF补偿后,本文所提控制方法下,各相电源电流正弦化,谐波含量大大降低,abc三相电源电流的THD值可分别降至3.32%,3.75%,3.72%,远小于传统PI控制方法下的7.24%,7.38%,7.49%;对比图A4(b)和图A5(b),在本文控制方法、传统PI控制方法下,直流侧的总电压的稳定时间分别为0.06 s和0.14 s,本文方法的响应速度更快;由图A4(c)和图A4(d)可见,SAPF侧输出相电压为三电平,上、下直流侧电容两端电压能维持在设定值400 V左右;且由附录A图A5(c)可见,本文所提控制方法下,上、下直流侧电容两端电压之差更小,可低于±5 V。附录A表A1即为两种控制策略在电网电压不平衡条件下的仿真比较结果。

3.3 电网电压相角不平衡时的控制性能分析

abc三相电源电压的有效值均为220 V,但abc三相的相角分别为0°,-90°,60°,此时电网电压的相角不平衡,无加载和卸载过程。仿真结果如附录A图A6所示。由该图可见,经本文控制方法下的SAPF补偿后,能够达到电源电流正弦化、电网功率因数单位化和谐波补偿的目的。其中a相电源电流的THD值可由59.51%下降至3.52%,大大减小了谐波含量。

4 硬件实验分析

为了进行NPC型三电平SAPF的实验研究,搭建了硬件实验平台。该实验平台主要包括与仿真参数相同的交流源、阻感负载、型号为TMS320F28335的DSP控制器、NPC型三电平逆变器(由12个型号为IKW30N60T的绝缘栅双极型晶体管和6个型号为VS-30EPF12的二极管构成),如附录A图A7所示。

图4为三相电源电压有效值均为220 V、突然接入相同负载,稳定后又断开该负载时,a相电源电流、负载电流、SAPF输出电流和直流侧上、下电容两端电压的实验波形图;附录A图A8为三相电源电压有效值分别为220,150，192 V时,三相电源电压、a相负载电流、本文方法下a相电源电流和传统PI控制方法下a相电源电流的波形图;附录A图A9为三相电源电压有效值均为220 V且相角分别为0°,-90°,60°时,三相电源电压、a相负载电流、a相电源电流和SAPF输出侧线电压的波形图。

图4 电网平衡时的实验结果Fig.4 Experimental results under balanced power grid

由硬件实验结果可知,经本文所提方法控制下的SAPF能有效补偿谐波和无功电流,使直流侧总电压达到给定值,同时保证直流侧差压约为0,且具有良好的动静态特性,与传统PI控制方法相比,补偿效果更好。因此,硬件样机上的实验结果也验证了本文方法的正确性和有效性。

5 结语

本文对NPC型三电平SAPF的数学模型进行了分析,提出了SAPF基于Lyapunov函数的非线性控制策略的新型控制方法,该方法可以在三相电网不平衡的条件下改善电流谐波和抑制电流波动,这种优势决定了该方法具有很高的实际应用价值,例如:可以高效地滤除负荷电流中的高次谐波,从而使得配电网清洁高效,满足国标对配电网谐波的要求;可高效率地消除因谐波、电压跌落、相角不平衡引起的系统不平衡问题。但是,当环境极其恶劣的时候,控制增益的选择非常困难,这种控制方法的优势也就不再明显。最后,通过软件仿真和硬件实验得到如下结论。

1)根据被控对象在dq0坐标系下的一般数学模型,结合Lyapunov理论,提出了电流内环基于Lyapunov函数的控制器的设计方法。与传统的PI控制方法相比,本文所提的控制方法无需对谐波的正负序分量进行处理,具有很强的鲁棒性。

2)基于Lyapunov函数的非线性控制策略结构简单,可调参数少(仅为控制增益α),能显著提高SAPF的动态响应速度,且能够在电网平衡/不平衡条件下,快速有效地对谐波和无功功率进行补偿,实现电网电流正弦化,进一步降低谐波含量。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] ACUNA P, MORAN L, RIVERA M, et al. Improved active power filter performance for renewable power generation systems[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 687-694.

[2] 许晓彦,杨才建,MINDYKOWSKI J.有源滤波器空间矢量脉宽调制电流跟踪算法的优化[J].电力系统自动化,2012,36(4):80-84.

XU Xiaoyan, YANG Caijian, MINDYKOWSKI J. Optimization on current tracking algorithm in active power filter based on SVPWM[J]. Automation of Electric Power Systems, 2012, 36(4): 80-84.

[3] 周京华,贾斌,章小卫,等.混合式三电平中点电位平衡控制策略[J].中国电机工程学报,2013,33(24):82-89.

ZHOU Jinghua, JIA Bin, ZHANG Xiaowei, et al. A hybrid three-level neutral-point balance control strategy[J]. Proceedings of the CSEE, 2013, 33(24): 82-89.

[4] ANTONIEWICZ K, JASINSKI M, KAZMIERKOWSKI M P. Model predictive control for three-level four-leg flying capacitor converter operating as shunt active power filter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 5255-5262.

[5] 李达义,孙玉鸿,熊博,等.一种并联型有源电力滤波器的新型控制方法[J].电力系统自动化,2014,38(15):112-117.DOI:10.7500/AEPS20131030009.

LI Dayi, SUN Yuhong, XIONG Bo, et al. A novel control method for shunt active power filter[J]. Automation of Electric Power Systems, 2014, 38(15): 112-117. DOI: 10.7500/AEPS20131030009.

[6] DEY P, MEKHILEF S. Current harmonics compensation with three-phase four-wire shunt hybrid active power filter based on modified D-Q theory[J]. IET Power Electronics, 2015, 8(11): 2265-2280.

[7] 谭兴国,王辉,张黎,等.容错型三相四开关有源电力滤波器及其控制策略[J].电力系统自动化,2014,38(18):99-104.DOI:10.7500/AEPS20130708003.

TAN Xingguo, WANG Hui, ZHANG Li, et al. Fault-tolerant active power filter based on three-phase four-switch topology and its control strategy[J]. Automation of Electric Power Systems, 2014, 38(18): 99-104. DOI: 10.7500/AEPS20130708003.

[8] 蒋正荣,黄波,李正熙.三电平有源电力滤波器中点电位平衡控制[J].电力电子技术,2015,49(1):88-89.

JIANG Zhengrong, HUANG Bo, LI Zhengxi. A neutral-point potential balancing algorithm for three-level APF[J]. Power Electronics, 2015, 49(1): 88-89.

[9] 胡健,陈文宪,陈冬冬,等.基于中线电流注入的三电平有源电力滤波器中点平衡策略[J].电网技术,2014,38(11):3165-3170.

HU Jian, CHEN Wenxian, CHEN Dongdong, et al. A neutral current injection based neutral point potential control strategy for neutral point clamping based tri-level shunt active power filter[J]. Power System Technology, 2014, 38(11): 3165-3170.

[10] 韩伟,王大志,李云路,等.基于Lyapunov函数的混合型有源电力滤波器控制策略[J].控制理论与应用,2014,31(9):1174-1181.

HAN Wei, WANG Dazhi, LI Yunlu, et al. Lyapunov-function-based control strategy for hybrid active power filter[J]. Control Theory & Applications, 2014, 31(9): 1174-1181.

[11] LI Tianhua, FEI Juntao. Feedback linearization control of a shunt active power filter using a fuzzy controller[J]. International Journal of Advanced Robotic Systems, 2013, 10(9): 332-338.

[12] FOGLI G A, DE ALMEIDA P M, RODRIGUES V M, et al. Sliding mode control of a shunt active power filter with indirect current measurement[C]// IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), November 29-December 2, 2015, Fortaleza, Brazil: 5p.

[13] 薛花,王育飞.基于无源性的并联型有源滤波器自适应滑模控制[J].电力自动化设备,2011,31(9):60-64.

XUE Hua, WANG Yufei. Passivity-based adaptive sliding mode control of shunt active filters[J]. Electric Power Automation Equipment, 2011, 31(9): 60-64.

[14] LI Lanfang, YANG Honggeng, GUO Weiming, et al. Analysis and application of Lyapunov-based stable control of the single-phase shunt active power filter[C]// IEEE PES Asia-Pacific Power and Energy Engineering Conference, March 27-29, 2012, Shanghai, China: 4p.

[15] 吴可丽,夏长亮,张云,等.二极管钳位型三电平逆变器共模电压抑制[J].电工技术学报,2015,30(24):110-117.

WU Keli, XIA Changliang, ZHANG Yun, et al. Common-mode voltage suppression for neutral-point-clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 110-117.

[16] 周京华,柴小丰,祝天岳,等.三电平有源电力滤波器谐波电流及中点电位平衡控制[J].电网技术,2017,41(6):2012-2019.

ZHOU Jinghua, CHAI Xiaofeng, ZHU Tianyue, et al. Control of harmonic current and neutral-point potential balance for three-level active power filter[J]. Power System Technology, 2017, 41(6): 2012-2019.

[17] 薛花,范月,王育飞.基于李雅普诺夫函数的并联型混合有源电力滤波器非线性控制方法[J].电工技术学报,2016,31(21):133-141.

XUE Hua, FAN Yue, WANG Yufei. Nonlinear control strategy based on Lyapunov function for shut hybrid active power filter[J]. Transactions of China Electrotechnical Society, 2016, 31(21): 133-141.

[18] RAHMANI S, HAMADI A, AL-HADDAD K. A Lyapunov-function-based control for a three-phase shunt hybrid active filter[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1418-1429.

[19] MISSANDA A, AL-HADDAD K, MENDALEK N. Nonlinear control of three-phase three-level four-wire NPC converter[C]// IEEE International Conference on Industrial Technology (ICIT), March 14-17, 2016, Taipei, China: 1254-1259.