基于堆叠自编码网络的风电机组发电机状态监测与故障诊断

赵洪山, 刘辉海, 刘宏杨, 林酉阔

(华北电力大学电气与电子工程学院, 河北省保定市 071003)

0 引言

风能作为一种清洁、可再生的绿色能源,近年来得到了快速发展。由于环境恶劣、工况复杂,风机极易发生故障,但对于发电机等驱动链部件的故障是造成风机停机的主要原因[1-2]。因此,可以对发电机故障进行预测,从而降低发电机的运行风险及损失。

发电机包含多个子系统,其故障种类具有多样性[3-5]。目前,风电机组发电机的状态监测方法主要有振动监测、油液监测分析和电参数监测[6-9]等方法。文献[10-12]利用线性回归方法处理得到消除输出功率和环境温度影响后的监测模型,通过残差异常变化分析发电机的故障。基于振动监测的研究中,文献[13-14]通过对发电机振动信号降噪处理提取故障特征,实现了对故障部位和失效程度的识别。另外,通过分析驱动链上的转矩测量信号,结合载荷的异常变化可以分析出发电机的故障[15]。文献[16]提出采用油液传感器对油液进行在线实时监测,通过分析油液压力和杂质成分实现对发电机的状态监测与故障诊断,但油液传感器的安装增加了成本。近年来,深度学习作为大数据分析的一种新方法,摆脱了人为因素的不确定性和诊断技术经验的依赖性,直接从大量数据中智能提取参数间的特征关系[17-19]。

目前深度学习的研究主要是利用故障样本进行训练,实现设备的故障分类和识别。然而实际中大量故障样本难以全面收集,从而给该类算法的应用带来了一定的困难。本文基于风电机组发电机正常状态下数据采集与监控(SCADA)数据样本,提出堆叠自编码(stacked autoencoder,SAE)深度学习网络模型。首先利用SAE网络深层学习发电机SCADA数据内部蕴含的关系,提取发电机的状态监测量。结合自适应阈值检测状态监测量的趋势变化,实现故障判定,进一步利用变量残差趋势的异常变化分析出故障原因。

1 SAE网络

1.1 模型预训练

深度学习网络包含一系列逐层提取输入数据深层特征的深度神经网络模型。该网络通过对数据非监督学习逐层初始化参数,然后采用监督学习的方式进行微调。深度学习网络模型可以在高层表示更加抽象和复杂的数据特征或属性,并且这种通过学习获取的变量间的特征规则不会随着输入数据的改变而变化[20]。本文引入SAE网络模型逐层提取发电机SCADA数据蕴含的特征和变量间的关系,实现对发电机异常的分析。

自编码(autoencoder,AE)网络包含一个含有d个单元的可视层,一个含有h个节点的隐含层,以及一个含有d个节点的重构层和激活函数f,如图1所示。

图1 自编码网络模型结构Fig.1 Structure of AE network

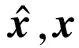
y=f(Wyx+a)

(1)

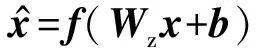
(2)

式中:Wy和Wz分别为输入与隐含层和隐含层与输出的权重,并且Wy=Wz=W;a和b分别表示隐含层单元偏置和输出层单元偏置;f(·)表示激活函数,选取Sigmoid函数。因此,在网络逐层学习训练的过程中，需要确定的参数θ=[W,a,b]。

深度学习网络的目标是最小化输入值与重构值的误差E,即

(3)

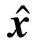
自编码网络的基本结构为限制玻尔兹曼机(restricted Boltzmann machine,RBM),其中RBM包含m个可见单元v的可见层和n个隐含单元h的隐含层,如图1中结构所示。在RBM中(v,h)∈{0,1},由吉布斯分布可以得到其单元节点的联合分布为:

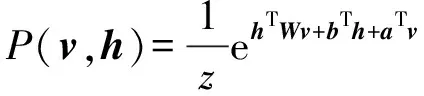
(4)

式中:z为标准化常数。

RBM中隐含层与可见层单元节点的能量函数表示为:

E(v,h)=-hTWv-bTh-aTv

(5)

根据RBM的结构,隐含层与可见层的条件概率分布由能量函数表示为:

P(vi=1|h)=f(ai+Wyh)

(6)

P(hj=1|v)=f(bi+Wzv)

(7)

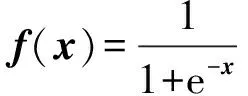
(8)

Sigmoid函数能够抑制两头使得网络对中间细微变化敏感，因而对特征识别度更好，故本文选择Sigmoid函数作为激活函数f(x)。

RBM的结构学习的结果是最大限度地拟合输入数据,这种接近程度可以通过重构误差Re描述:

(9)

基于重构误差,针对训练数据集x,损失函数可以表示为式(10),其中N为训练数据集x的长度。通过利用梯度下降法对整体损失函数极小化处理,从而达到网络参数的更新,求得参数θ。那么网络权重的更新准则可以定义为:

(10)

(11)

(12)

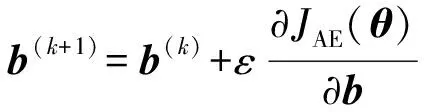
(13)

式中:ε为初始学习率。

对于每个RBM训练完成之后,将隐含层的输出作为更高一级的输入,同时训练下一级的网络参数,直到完成整个自编码网络的参数训练。自编码网络的单元RBM每层的激活信息可表示为学习到的发电机参数间的关系特征,并通过逐层学习提取高表征能力的特征。将多个自编码器的输入层和隐含层连接起来构成SAE网络,该模型可以提取发电机状态变量数据的更深层特征。图2显示了典型的SAE网络结构。为了尽可能监测发电机的运行状态,选择发电机的SCADA数据变量作为模型可见层的输入,选取发电机状态变量如附录A表A1所示。

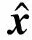
图2 SAE网络结构Fig.2 Structure of SAE network

由于风电机组发电机不同类型变量的数值差异性比较大,为了减小数据的差异性引起计算误差,并保证原始数据结构相对不变,对各变量进行归一化处理。

当学习网络建立之后,提取的数据特征保留在隐含层中,隐含层的输出可以作为更高一层的输入提取更深层的特征。如果模型能够非常好地将y恢复为初始输入,即得到输入的重构值,这里输入变量与输出变量相对应并且具有相同的物理意义,那么这就意味着训练得到的模型参数保留了输入数据足够丰富的信息特征。因此,将自编码网络连接形成更深层的SAE训练模型,并最小化整个输入的信息损失,从而使该网络保留了数据内部不变的复杂特征。因此,构建SAE网络来提取风电机组发电机SCADA状态监测数据蕴含的规则特征。

1.2 模型建立

在SAE模型的预训练结束后,实现了对编码网络每个隐含层参数的初始化,从而建立发电机SAE模型的初始架构。SAE网络的预训练是对发电机状态监测数据集规则的非监督学习,学习的结果可以作为SAE模型监督学习的先验值。根据发电机长期正常运行状态下的SCADA标签数据集,采用反向传播(BP)算法进行监督学习,从而实现对网络参数的优化和参数表征数据规则能力的改善。由该训练过程得到的参数比单纯BP算法的训练效果要好,由于调优训练只需要在预训练获得的参数基础上进行局部搜索,明显缩短了收敛时间[21]。

风电机组发电机正常运行状态下的SCADA数据满足稳定的内部关联,SAE网络提取的变量间的固有关系以网络参数的形式保存,利用该网络能够最大限度地拟合输入数据。因此,利用正常样本数据得到的重构误差Re一直保持在一定范围内波动,并且趋势相对稳定。当发电机发生异常时,其数据蕴含的内部关联将会被破坏,反映到重构误差Re的趋势变化中,通过设定阈值及时地判别出故障,从而达到状态监测的目的。因此,选择Re作为发电机的状态分析量,正常状态下的Re变化如图3所示。

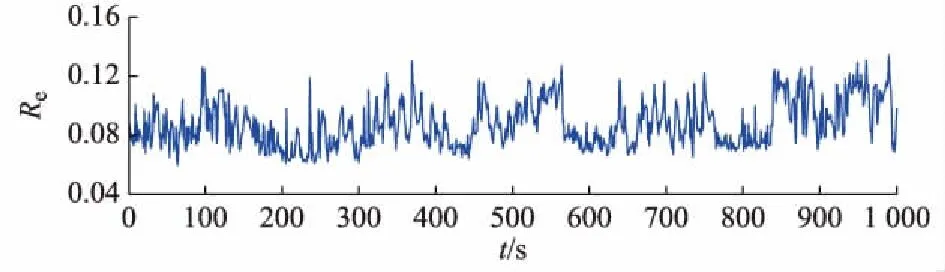
图3 正常状态下的A30号风电机组发电机的ReFig.3 Re of wind turbine generator A30 under normal conditions

1.3 SAE网络的在线训练

在工程实际中,模型训练完成之后,可以对发电机的状态进行监测。一段时间之后,利用发电机SCADA系统采集的新的状态数据作为训练集,在原有训练参数的基础上,对模型实现在线训练更新模型参数。在线训练的优点在于发电机运行一段时间的数据量较小,并且在已经稳定的网络框架上进行学习训练,在改善网络参数稳定性的同时,降低了重新训练网络的时间。另外在线训练达到对特征规则的递进学习,从而使得特征提取更充分,避免了重新初始学习的复杂性。初始训练Re与在线训练Re的对比如图4所示。从图中可以看出,在线学习之后的网路重构误差较小,这表明在线学习的网络损失的信息少,具有较强的稳定性。

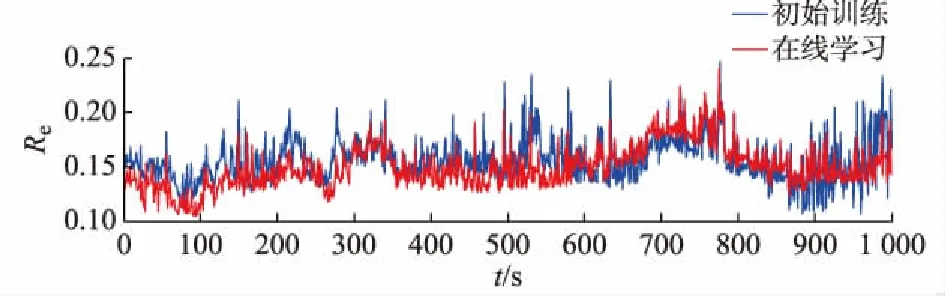
图4 初始训练Re与在线训练Re对比Fig.4 Comparison of initial training Re and online training Re

1.4 发电机故障识别分析

利用重构误差预测出风机发电机部分的异常后,可以根据SCADA数据每个变量的变化行为,并结合设备的物理特性来识别和估计可能的故障类型或故障范围。

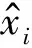
(14)

2 自适应阈值设定

风机运行过程是一个动态非平稳过程,对于发电机的重构误差Re也处于动态变化中。因此为了有效判定Re的非平稳趋势,需要设定能够随着变量Re自适应变化的阈值。

考虑到风机运行的非平稳性,Re含有噪声并且波动性较大,该自适应阈值的产生首先需要运用自回归滑动平均模型和指数平滑处理算法实现对Re的滤波和平滑处理[22]。然后利用处理之后的重构误差值计算自适应阈值。该方法与传统方法的不同之处在于,告警阈值不仅是基于标准差计算得到,而且考虑到了Re含有的噪声因素。滤波和平滑处理之后的重构误差趋势变化波动小,Re的标准差σ也相对较小。因此,如果自适应预警阈值的计算基于±3σ,那么阈值会非常接近均值,将导致误报警。通过计算初始重构误差较大的标准差,并使得阈值随Re的变化而变化可以减少误报警。

这里重构误差中的噪声通过平均变化率来衡量,如式(15)所示。将得到的噪声值加到原始重构误差的标准差σ中来计算告警阈值,如式(16)所示。

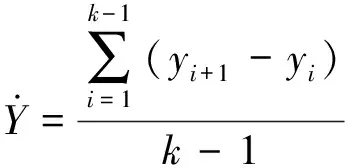
(15)

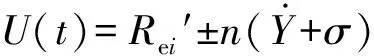
(16)

当发电机工作异常时,重构误差Re的分布特性被破坏,重构误差值落在控制范围外,表现为重构误差的趋势变化越过阈值,从而判定发电机发生异常。实际中发电机参数的阈值一般设定较高,直接通过监测这些参数的异常变化会对故障的判别具有一定的滞后性。因此利用自适应阈值判定Re的趋势异常变化,可以较早地实现发电机故障判定。结合式(16)得到发电机异常状态判定准则为:

(17)

3 基于SAE模型发电机状态监测与故障诊断方法分析过程

风机正常状态下,发电机的Re的波动变化一直受控于其自适应阈值范围内,当Re趋势变化越过阈值,并且趋势保持在控制线之上,则可以判定发电机发生了异常。基于SAE模型的风机发电机状态监测与故障诊断分析过程如下:首先选取发电机正常状态下的SCADA数据建立数据集,并对每个变量进行归一化处理后分为训练集和测试集;采用训练集中的无标签样本利用对比散度算法对SAE网络进行逐级预训练;选用发电机训练数据集中的标签样本,运用BP算法对预训练之后的网络参数进行优化;依据建立的发电机SAE网络模型,计算测试数据集的Re,构成Re序列;引入Re的自适应阈值检测其趋势变化,当Re超过控制线时判定发电机发生异常;当判定异常发生之后,根据状态变量的残差趋势变化判定发电机的具体异常变量,分析出可能故障原因。

4 算例分析

4.1 数据采集与参数设定

本文中选取某实际风电场1.5 MW A01号风机发电机、A12号风机发电机和A04号风机近两年正常状态下的SCADA状态监测数据建立训练样本集,可以使得网络能够充分描述正常运行状态下(不同风况、不同季节等)的特征,以满足故障检测的需要。另外对发电机的SAE网络模型进行参数训练,并通过SCADA数据的更新实现模型的在线学习。其中电流、电压为当前时刻的有效值,其他参数均为当前时刻记录的瞬时值。

针对多台风机数年正常工况下的运行数据作为模型的训练数据集,分别选取不同的隐含层数和RBM的初始化参数构建SAE网络模型,并对网络的重构误差进行分析和对比,发现当发电机的SAE模型设定4个隐含层,每个隐含层的单元数分别为1 000,500,250,50,SAE模型的参数W,a,b初始化为服从高斯分布的随机较小值,初始学习率ε设为0.1,网络更新速率设为0.001时,这组参数能够更好地保留训练数据集的信息,而且当利用多组数据样本验证后,该组参数具有很好的稳定性。因此,最终本文选取了保留风机信息损失最少的最佳参数作为该模型的基本参数来进一步训练SAE网络。根据Re越小模型越优,综合考虑迭代周期对训练时间的影响,选择参数调优的迭代周期为200。

4.2 基于SAE模型的发电机状态监测分析

在建立SAE模型之后,利用A01号机组故障前后一段时间的发电机SCADA数据进行测试,仿真结果如附录A图A1所示,Re由式(9)计算得到。从仿真结果中可以看出,发电机的监测变量Re在60 h时趋势发生改变,偏离原有的动态平稳趋势,然而此时的实际风速约为9 m/s,正常状态下Re的趋势不会发生较大的波动。经过约3 h后Re越过阈值并保持在阈值之上,从而判定发生异常,实际中此时发出预警信号。对比基于SCADA参数的多元线性回归分析建立模型对该发电机状态进行分析,如附录A图A2所示。通过附录A图A2发现,利用线性回归分析的残差趋势变化比较缓慢,不能及时、准确地反映出发电机状态。

利用式(9)和SAE网络计算得到A12机组的Re,其变化趋势如附录A图A3所示。附录A图A3显示发电机的重构误差Re在0～13 h内一直处于控制阈值范围内,12.5 h时Re开始呈现上升趋势,经过40 min越过阈值。然而此时的风速并没有剧烈波动,通常正常状态下不会出现Re急剧变化的情况,这表明该发电机出现了异常。随后Re的趋势上升速度加快,并一直处于阈值之上,从而判定发电机出现异常,该分析结果与实际发电机状态信息相一致。结合多元线性回归分析的残差分析发电机的状态,如附录A图A4所示,可以发现回归模型残差趋势虽然能够反映发电机状态的异常,但残差趋势变化不够灵敏,在实际应用中对于及时发出故障预警存在不足,对比可以发现SAE网络的Re能够较早地发出异常预警。

A04号风机故障案例为发电机碳刷磨损故障,利用发电机SCADA数据建立SAE网络,并测试故障记录数据,得到该发电机的Re变化趋势,如附录A图A5所示。从图中可见在32 h时Re越过阈值,发出异常预警,但经过约2 h后Re回到其控制阈值范围内。最终在51 h时Re再次越过阈值,并一直保持在阈值之上,直到故障停机。结合实际的故障处理验证了该故障的判断。

在机组正常运行状态下,发电机处于动态平衡状态,各SCADA状态监测变量之间满足固有的内部联系,反映到监测变量的趋势变化表现为具有一定的波动性,但保持一定的相对稳定趋势。在发电机发生异常时,状态监测变量间失去长期稳定关系,对于反映整体状态的监测量Re的趋势发生改变,偏离原有的稳定趋势。A01,A12和A04号机组发电机的实验结果验证了故障之后参数间的关系被打破之后Re趋势的改变。

4.3 基于SAE模型的发电机故障诊断分析

发电机的异常通常由某部位的变量的异常变化反映出来。随着异常的进一步发展,发电机的运行状态可能对机组发电量造成影响。在正常情况下,变量经过SAE模型的重构值最大限度地拟合输入。结合本文故障诊断方法,当某个变量残差趋势在发电机故障后发生明显变化时,则可以通过该变量判断可能的故障原因,实现对发电机故障的初步诊断。A01号风机发电机通过Re的趋势变化检测出异常之后,利用式(14)进一步分析发电机变量的残差变化,如附录A图A6所示。

结合附录A图A1,从附录A图A6(a)的残差结果中可以看出,发电机的绕组温度残差趋势在Re的趋势发生变化的同时呈现上升趋势。此时绕组温度升高,使得Re的趋势和绕组残差趋势发生变化。另一方面随着绕组温度的上升,A01号风机的功率残差偏向小于零值,并且变化比较剧烈。此时发电机绕组温度的升高导致发电机的发电功率与相同风速正常状态下的发电功率相比减小,如附录A图A6(b)所示。其他变量的残差值一直在零值附近波动,没有明显的趋势变化,从而可以初步判定导致绕组温度升高的原因可能是负荷增大或者是发电机散热器出现问题。

对于A12号风机发生异常之后,发电机前后轴承的温度残差变化如附录A图A7(a)所示。从残差结果中可以看出,发电机后轴承温度残差在Re趋势发生变化的同时呈现上升趋势,其他变量的残差值一直在零值附近波动,发电机的前轴承温度残差趋势没有明显变化,而后轴承b的温度残差呈明显上升,这表明实际中发电机后轴承b的温度已经明显偏离其长期正常的温度值,并且温度正在逐渐升高。附录A图A7(b)中的风机功率残差曲线在发电机发生异常之后,发电功率与相同风速正常状态下相比受到一定的影响。因此根据故障与变量的关系可以判断,可能是发电机后轴承油脂不足导致轴承磨损，使得温度升高影响功率输出。

本文针对风机多个SCADA运行参数包含丰富的状态信息,建立了发电机多个变量的SAE预测模型,该模型可以全面反映风机发电机的状态,并通过实验分析验证了该方法的有效性。另外,一旦利用充足的正常数据样本训练完成风机SAE网络之后,其模型参数包含正常状态下全面的信息特征,因此利用每秒或每分钟(一个较短的时间段)的SCADA数据作为已经建立好的SAE模型的输入,直接计算得到反映状态的Re, 计算量不大且可以实现在线预测使用。

5 结语

针对风力发电机的状态监测与故障诊断方法的研究,本文提出基于发电机SCADA数据的SAE网络深度学习方法。实际故障分析验证了深度学习方法的有效性,并达到了故障初步诊断的目的。

本文研究方法通过提取风机多个SCADA参数的内部关系,定义了单个监测量实现对发电机异常的判定。该方法可以被进一步推广到风机其他关键部件,如主轴承和齿轮箱。另外,在线训练可以实现网络参数的递进学习更新,从而使得特征提取更加充分,为该方法实现风机部件的在线状态监测提供了可能性。本文方法可以实现渐变式故障预测,但未能实现对故障进行识别和诊断。因此,可以进一步与其他的故障诊断算法相结合或采用充足故障样本训练网络实现故障的诊断。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 马婧华,汤宝平,韩延,等.风电机组传动系统网络化状态监测与故障诊断系统设计[J].重庆大学学报,2015,38(1):34-37.

MA Jinghua, TANG Baoping, HAN Yan, et al. Wind turbine transmission network status monitoring and fault diagnosis system design[J]. Journal of Chongqing University, 2015, 38(1): 34-37.

[2] 陈雪峰,李继猛,程航,等.风力发电机状态监测与故障诊断技术的研究与进展[J].机械工程学报,2011,47(9):45-52.

CHEN Xuefeng, LI Jimeng, CHENG Hang, et al. Research and application of condition monitoring and fault diagnosis technology in wind turbines[J]. Journal of Mechanical Engineering, 2011, 47(9): 45-52.

[3] 尹浩霖.基于小波分析和神经网络的风力发电机组故障诊断[D].西安:西安理工大学,2014.

[4] LICARI J, EKANAYAKE J, MOORE I. Inertia response from full-power converter-based permanent magnet wind generators[J]. Journal of Modern Power Systems and Clean Energy, 2013, 1(1): 26-33.

[5] 梁颖,方瑞明.基于SCADA和支持向量回归的风电机组状态在线评估方法[J].电力系统自动化,2013,37(14):7-12.

LIANG Ying, FANG Ruiming. An on-line wind turbine condition assessment method based on SCADA and support vector regression[J]. Automation of Electric Power Systems, 2013, 37(14): 7-12.

[6] QIAO Wei, LU Dingguo. A survey on wind turbine condition monitoring and fault diagnosis: Part Ⅱ signals and signal processing methods[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6546-6557.

[7] 李辉,杨东,杨超,等.基于定子电流特征分析的双馈风电机组叶轮不平衡故障诊断[J].电力系统自动化,2015,39(13):32-37.DOI:10.7500/AEPS20140830004.

LI Hui, YANG Dong, YANG Chao, et al. Blade imbalance fault diagnosis of doubly fed wind turbines based on stator current feature analysis[J]. Automation of Electric Power Systems, 2015, 39(13): 32-37. DOI: 10.7500/AEPS20140830004.

[8] 马宏忠,张正东,石维俊,等.基于转子瞬时功率谱的双馈风力发电机转子绕组故障诊断[J].电力系统自动化,2014,38(14):30-35.DOI:10.7500/AEPS20130808012.

MA Hongzhong, ZHANG Zhengdong, SHI Weijun, et al. Doubly-fed induction generator stator fault diagnosis based on rotor instantaneous power spectrum[J]. Automation of Electric Power Systems, 2014, 38(14): 30-35. DOI: 10.7500/AEPS20130808012.

[9] POPA L M, JENSEN B B, RITCHIE E, et al. Condition monitoring of wind generators[C]// Conference Record of the 38th IAS Annual Meeting, October 12-16, 2003, Salt Lake City, UT, USA: 1839-1846.

[10] 霍娟,唐贵基,刘大宾,等.基于温度信号的风电机组发电机实时可靠性监测新方法[J].可再生能源,2016,34(3):408-412.

HUO Juan, TANG Guiji, LIU Dabin, et al. A novel monitoring method of wind turbine generator real-time reliability based on temperature signals[J]. Renewable Energy Resources, 2016, 34(3): 408-412.

[11] DING N, LU Z, QIAO Y, et al. Simplified equivalent models of large-scale wind power and their application on small-signal stability[J]. Journal of Modern Power Systems and Clean Energy, 2013, 1(1): 58-64.

[12] GUO P, INFIELD D, YANG X. A wind turbine generator condition-monitoring using temperature trend analysis[J]. Transactions on Sustainable Energy, 2012, 3(1): 124-132.

[13] 庄哲民,殷国华,李芬兰,等.基于小波神经网络的风力发电机故障诊断[J].电工技术学报,2009,24(4):224-228.

ZHUANG Zhemin, YIN Guohua, LI Fenlan, et al. Fault diagnosis of wind power generation based on wavelet neural network[J]. Transactions of China Electrotechnical Society, 2009, 24(4): 224-228.

[14] CASELITZ P, GIEBHARDT J. Rotor condition monitoring for improved operational safety of offshore wind energy converters[J]. Journal of the Textile Institute, 2005, 127(2): 253-261.

[15] WILKINSON M R, SPINATO F, TAVNER P J. Condition monitoring of generators & other subassemblies in wind turbine drive trains[C]// IEEE International Symposium on Diagnostics Electric Machines, Power Electronics and Drives, September 6-8, 2007, Cracow, Poland: 388-392.

[16] ZHU J, YOON J M, HE D, et al. Online particle contaminated lubrication oil condition monitoring and remaining useful life prediction for wind turbines[J]. Wind Energy, 2015, 18(6): 1131-1145.

[17] 雷亚国,贾峰,周昕,等.基于深度学习理论的机械装备大数据健康监测方法[J].机械工程学报,2015,51(21):49-56.

LEI Yaguo, JIA Feng, ZHOU Xin, et al. A deep learning-based method for machinery health monitoring with big data[J]. Journal of Mechanical Engineering, 2015, 51(21): 49-56.

[18] 薛禹胜,赖业宁.大能源思维与大数据思维的融合:(一)大数据与电力大数据[J].电力系统自动化,2016,40(1):1-8.DOI:10.7500/AEPS20151208005.

XUE Yusheng, LAI Yening. Integration of macro energy thinking and big data thinking: Part one big data and power big data[J]. Automation of Electric Power Systems, 2016, 40(1): 1-8. DOI: 10.7500/AEPS20151208005.

[19] WORDEN K, STASZEWSKI W J, HENSMAN J J. Natural computing for mechanical systems research: a tutorial overview[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 4-11.

[20] 赵光权,葛强强,刘小勇,等.基于DBN的故障特征提取及诊断方法研究[J].仪器与仪表学报,2016,37(9):1946-1953.

ZHAO Guangquan, GE Qiangqiang, LIU Xiaoyong, et al. Fault feature extraction and diagnosis method based on deep belief network[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1946-1953.

[21] CHEN Yushi, LIN Zhouhan, ZHAO Xing, et al. Deep learning-based classification of hyperspectral data[J]. IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing, 2014, 7(6): 2094-2107.

[22] WILLETTS R, STARR A G, DOYLE A, et al. Generating adaptive alarms for condition monitoring data[J]. International Journal of Comadem, 2005, 8(3): 149-155.