基于电压源型换流器的多端直流配电网潮流计算
吴红斌, 杨 超, 陈 煜, 王刘芳, 徐 斌
(1. 合肥工业大学电气与自动化工程学院, 安徽省合肥市 230009; 2. 国网安徽省电力公司经济技术研究院, 安徽省合肥市230022; 3. 国网安徽省电力公司电力科学研究院, 安徽省合肥市 230601)
0 引言
随着新能源的发展与应用,越来越多的分布式电源(包括风机、光伏等直流形式的电源)接入配电网,以及电动汽车、信息设备、半导体照明系统、直流电机等直流负荷的日益增长,现有交流配电网将面临电能接纳与供应的稳定性、高效性、经济性等方面的巨大挑战;另一方面,随着电力电子技术的发展及全控器件的成熟应用,将基于电压源型换流器(voltage source converter,VSC)的直流技术运用到配电网供电领域,将有效解决城市配电系统面临的问题。因此,发展直流配电网将是未来城市配电网建设的必然趋势[1-4]。
由于VSC具有多种控制方式,使得直流配电网的整体运行和控制更加灵活[5-7],这对直流配电网的潮流计算提出了更高的要求。目前,直流配电网的研究还存在大量的理论与技术问题有待解决[8-10]。在分析直流配电网的稳态运行、设计相应控制方式和研究配备相关保护装置时,网络潮流计算都是重要的前提和基础。因此,有必要研究适用于直流配电网的潮流计算方法。
文献[11]详细推导了适用于VSC与多端直流(VSC-MTDC)系统潮流计算的VSC数学模型,提出了基于多端VSC与高压直流(VSC-HVDC)系统的交直流潮流交替迭代求解法。文献[12-14]提出了基于多端VSC-HVDC系统的交直流潮流统一迭代求解法。文献[15]提出一种基于双向迭代技术的交直流潮流计算的新算法,既保持了统一迭代法的收敛特性,又继承了交替迭代法控制方式切换简易的特点。文献[16]考虑了交流系统的三相不对称情况,采用序分量法推导了换流器潮流模型,并且根据换流器的不同控制策略提出不同的处理方法。上述文献研究的重点主要是换流器接口的等效处理及交直流混合潮流的迭代方法,较少详细考虑直流电压的控制方式,且多采用的牛顿—拉夫逊法,雅可比矩阵的形成与计算较为复杂。
本文重点研究直流配电网的潮流计算,详细分析了VSC稳态潮流模型及其直流侧控制方式,针对直流电网的不同电压控制策略,提出了一种适用于直流配电网潮流计算的改进前推回代算法:采用节点关联矩阵对网络结构进行自动搜索和自动开环处理;考虑了电压下垂控制方式,提出了针对环网和下垂节点的统一功率修正方法;考虑了VSC的功率限制及其控制方式的转换。最后,利用修改后的 IEEE 14节点直流配电网算例验证本文所提直流配电网潮流计算方法的有效性和正确性。
1 基于VSC的直流配电网潮流计算模型
1.1 VSC数学模型
忽略滤波器的损耗,VSC数学模型见图1。
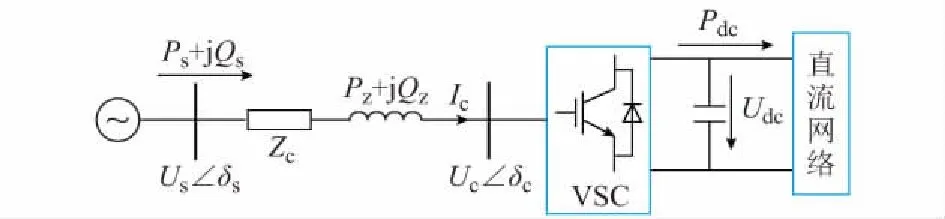
图1 VSC模型Fig.1 VSC model
图1中:Ps和Qs分别为与VSC相连的交流系统母线处有功功率和无功功率;Us∠δs为交流母线电压幅值相角;Uc∠δc为换流器交流出口处电压幅值相角;Zc=Rc+jXc为换流损耗的等效阻抗,其中Rc为换流电抗器与换流变压器的等效电阻之和,Xc为换流电抗器的等效电抗;Pdc为换流器直流侧有功功率;Udc为换流器直流侧电压。
换流器运行于整流状态和逆变状态的基本原理一致,以图中箭头所示方向为各相量的正方向,可推导出以下关系式。
Ps=Pz+Ploss+Pdc
(1)
式中:Pz为电阻Rc的有功损耗;Ploss为换流器内部损耗。
Pz和Ploss可用下式计算:
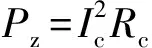
(2)
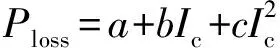
(3)

(4)
式中:Ic为流过换流器内部的交流电流;系数a,b,c均为常数,a模拟与Ic无关的固定有功损耗,b模拟与Ic成正比的有功损耗,c模拟与Ic平方成正比的有功损耗。
换流器流入直流侧的有功功率为:
Pdc=UdcIdc
(5)
VSC一般采用脉宽调制(pulse width modulation,PWM),存在以下关系式:
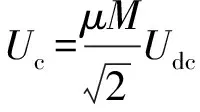
(6)

1.2 VSC控制方式
VSC可以通过d-q解耦的方法实现有功变量和无功变量的独立控制。其中d轴控制有功变量,主要影响直流侧潮流;q轴控制无功变量,主要影响交流侧潮流。换流器d轴的控制方式主要分3种。
1)定直流电压控制
换流站直流侧电压Udc保持恒定,即
Udc=Udcref
(7)
式中:Udcref为换流器直流电压参考值。
2)定有功功率控制
换流器直流侧注入有功功率Pdc保持恒定,即
Pdc=Pdcref
(8)
式中:Pdcref为换流器直流有功功率参考值。
3)电压下垂控制
换流器直流侧电压Udc与有功功率Pdc保持特定关系,换流器特性方程为:

(9)
式中:K为换流器下垂系数。
换流器q轴的控制方式有2种:①定US控制,交流母线电压幅值不变,此时换流器节点等效为交流侧的PV节点;②定QS控制,注入交流母线侧无功功率不变,此时换流器节点等效为交流侧的PQ节点。
1.3 VSC在交直流混合潮流计算中的等效处理
现有文献在计算交直流混合系统时,多数考虑的是定交流功率控制,即Ps已知不变,由于VSC损耗未知,需要对交流系统与直流系统进行多次交替迭代。本文重点考虑直流电网的控制,有功控制量为直流功率Pdc,只需对直流系统进行一次潮流计算。根据q轴控制方式的不同可将VSC等效为交流母线上的PQ或PV节点。交直流潮流计算流程图见附录A图A1,具体计算步骤如下。
步骤1:直流系统潮流求解得Pdc值,换流器交流母线有功功率初值取Ps=Pdc。
步骤2:交流系统潮流求解得Us,δs或Qs,δs。
步骤3:换流器求解,根据式(2)至式(4)求得换流器损耗Pz和Ploss,由式(1)更新Ps值。
重复步骤2和步骤3,直至前后两次迭代Ps差值小于收敛精度。
1.4 DC/DC变换器数学模型
对于多电压等级直流配电网,相邻的不同电压等级节点之间需通过DC/DC变换器相连。DC/DC变换器的功能相当于交流系统中的变压器,可采用类似于交流变压器的方式对其进行处理,DC/DC变换器数学模型如图2所示。

图2 DC/DC变换器模型Fig.2 DC/DC converter model
图2中,内阻R等效变换器的内部损耗,k为变换器变比,可得潮流计算关系式为:
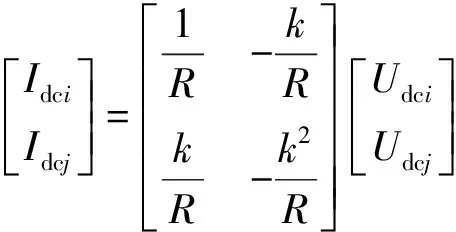
(10)
2 基于VSC的多端直流配电网控制策略
直流配电网便于中小型风电和光伏电站等新能源并网,各单元经过换流器接入直流母线,同时直流配电网通过换流器与不同交流配电网相连,当换流器的个数大于等于3个时,称为多端直流配电网[17]。
目前,尚没有成熟的直流配电网控制策略,主要参考柔性直流输电的电压控制策略,其中适用于直流配电网的控制策略主要有3种:主从控制、电压裕度控制、电压斜率控制[5]。
主从控制策略是指选取一端换流器作为主换流器,采用定直流电压控制方式,其余换流器作为从换流器,均采用定有功功率控制方式。直流电网主从控制策略下的电压—功率特性见附录A图A2。
电压裕度控制是指在主从控制的基础上设定一个后备换流器,系统正常运行主换流器采用定直流电压控制,后备换流器与各从换流器均采用定有功功率控制。当主换流器传输功率越限后,主换流器转为定有功功率控制(控制值为有功功率上限或下限),后备换流器转为定直流电压控制。直流电网电压裕度控制策略下的电压—功率特性见附录A图A3。
电压斜率控制是指选取多个换流器采用有功功率—电压下垂控制方式,其余多个换流器采用定有功功率控制。此控制策略下由采用有功功率—电压下垂控制的换流器根据各自的下垂特性曲线共同平衡有功功率,维持直流电压。直流电网电压斜率控制策略下的电压—功率特性见附录A图A4。
3 基于VSC的多端直流配电网潮流计算方法
3.1 网络结构自动搜索和开环处理
确定系统网络结构是配电网潮流计算的第一步。为了描述系统中节点与节点、节点与支路的连接关系,需要对系统的节点及支路进行编号,通常采用广度优先搜索法、深度优先搜索法等节点编号优化方法。这些特定的编号方法比较复杂,目前,已有文献对前推回代算法进行了改进,提出了与节点编号无关的网络结构搜索方法。但是这些方法只适用于纯辐射网且部分需要特定的数据输入形式,当存在环网时,需要先人为地进行开环处理。此外,直流配电网中VSC换流器存在多种控制方式,潮流计算可能出现平衡节点换流器由于功率越限而转换控制方式,进而导致直流平衡节点转移的情况。对于传统的前推回代潮流算法而言,这将改变各节点的父子关系,使潮流计算无法继续,需要根据新的平衡节点重新确定并输入直流网络的结构信息。
考虑到环网与平衡节点的转移,为保证潮流程序的连续性,提高计算效率,本文提出了一种基于节点关联矩阵的网络结构自动搜索与开环方法,避免了特定的节点编号规则与网络结构信息的重新输入。
对节点和线路进行自然编号,根据线路的首末端节点信息生成节点关联矩阵A,A为一个n×n阶矩阵,n为直流电网总节点数。当节点i与节点j之间有支路相连时,矩阵A中的元素aij和aji为1;相反,节点i与节点j之间无支路相连,则aij和aji为0;对角线元素aii均为0。
对于附录A图A5所示的8节点系统,其节点关联矩阵为:

(11)
显然,矩阵A是一个对称矩阵,对网络结构进行搜索时只需要用到节点关联矩阵的上三角或下三角元素即可。网络结构搜索的流程图见附录A图A6,该方法需要采用递归函数,从根节点(平衡节点)开始层层搜索,直至所有节点都搜索完成。具体搜索步骤如下。
步骤1:设置环网个数的变量为n1,令n1=0;设根节点即平衡节点为s号节点,执行步骤2。
步骤2:令ass=1,用以标记s号节点为已搜索;设置s号节点的子节点数量的变量为c,令c=0;寻找与s号节点相连的节点,对矩阵A中s行s列的下三角元素asj(1≤j 步骤3:令asb=0或abs=0,避免由b号节点反向搜索到s号节点,c=c+1;若abb=0,令b号节点为s号节点的第c个子节点,s号节点为b号节点的父节点,令s=b,返回步骤2;若abb=1,说明此节点已被搜索过,只有当网络中存在环网时才会出现这种重复的情况,令环网变量n1=n1+1,将b号节点设为开环点,其对应生成的虚拟节点号为n+n1,令n+n1号节点为s号节点的第c个子节点,s号节点为n+n1号节点的父节点,结束此分量的搜索。 步骤4:节点关系确定完成,复原节点关联矩阵A,令对角线元素aii=0,下三角元素等于上三角元素,即aij=aji(1≤j 在网络结构搜索过程中,在各环网处增加了与开环点对应的虚拟节点,潮流计算中虚拟节点作为功率节点处理,其初始电压为系统额定电压,初始功率设为0。每次迭代根据开环点与虚拟节点的电压差值对开环点以及虚拟节点的功率值进行修正,直至两节点的电压值相同(差值小于收敛精度)。修正过程中两节点的功率之和保持不变,为开环点的实际功率。 前推回代法适用于辐射状网络,对于环网需要进行开环处理,将环网变为辐射网进行计算。当所有节点电压标幺值近似为1.0时,开环后的环网关系式为: ΔP≈ΔI=R-1ΔU (12) 式中:ΔU为开环点与虚拟节点的电压差;R为环网的电阻矩阵;ΔI为由电压差引起的环路电流;ΔP为环网修正功率。ΔP,ΔI和ΔU为列向量,R为方阵,其维数均为环网数。每次潮流迭代后将ΔP和-ΔP分别叠加至开环点和虚拟节点。 以上为传统的前推回代算法对环网的处理方法,但其并未考虑直流电网中的下垂节点。对于直流电网中的Pdc-Udc下垂节点,其特性方程如式(9)所示,潮流计算时其稳定运行点未知,可先假设其节点注入功率为有功功率参考值,根据每次迭代后的节点电压值修正节点注入功率。但是,当下垂节点到平衡节点的支路与环网支路存在重合时,下垂节点的修正功率会在重合的支路上产生额外的电压降,对环网的修正功率值产生影响,如果分开计算环网和下垂节点的修正功率将导致潮流无法收敛。因此,必须对传统的环网潮流计算方法进行改进。本文算法在分析了下垂节点对环网修正功率影响的基础上,提出了一种适用于环网和下垂节点的统一功率修正方法。所建立的环网和下垂节点统一功率修正矩阵如式(13)所示,设环网数为h,下垂节点数为x。 (13) 式中:RH为h×h阶矩阵,其对角线元素为各环网所在支路的电阻之和,非对角线元素为环网之间的公共支路电阻之和(若公共支路的环网电流正方向相反,则累加时支路电阻取负值;若两环网之间无公共支路,取为零);RK为h×x阶矩阵,为环网支路与下垂节点至平衡节点之间支路的公共部分电阻之和;K为x×x阶对角阵,为各下垂节点的下垂系数。 假设直流电网的所有节点电压标幺值近似为1.0,可得 (14) 潮流计算时,每次迭代根据式(14)计算出环网和下垂节点的修正功率,分别叠加至开环点、虚拟节点和下垂节点,得到下次迭代开环点、虚拟节点和下垂节点的节点功率值为: (15) 当直流电网采用电压斜率控制策略时,由多个VSC采用Pdc-Udc下垂控制共同调节直流电压,直流电网中不存在严格的恒定电压点作为潮流计算的平衡节点,选取容量大且下垂系数小的VSC节点作为代平衡节点,以下垂特性方程给定的直流电压参考值为电压初值进行潮流求解,再根据求解的有功功率更新平衡节点电压,继续进行潮流求解直至前后两次迭代平衡节点电压差值小于收敛精度。 潮流计算收敛后,需要校验平衡节点和下垂节点VSC的有功功率是否越限,VSC传输的有功功率应满足: Pdc,min≤Pdc≤Pdc,max (16) 式中:Pdc,min为VSC有功出力下限;Pdc,max为VSC有功出力上限。 对于发生功率越限的VSC,其控制方式转换为定有功功率控制,有功控制值取其上下限值。若平衡节点越限,则后备换流站转换为定直流电压控制,平衡节点转移,重新确定网络结构进行潮流计算;若下垂节点越限,则下垂节点数减少,需重新形成功率修正矩阵进行潮流计算。 本文提出的基于前推回代的潮流计算流程图见附录A图A7,具体步骤如下。 步骤1:形成节点关联矩阵,确定VSC控制方式。 步骤2:搜索网络结构、设置开环点。 步骤3:初始化节点电压。 步骤4:前推计算支路电流。即 (17) 步骤5:回代计算节点电压。即 (18) 式中:Rij为节点i与节点j之间的支路电阻。 步骤6:收敛判断。若收敛,则执行步骤7,否则修正环网和下垂节点功率,返回步骤4。 步骤7:功率越限校验。若无越限,则结束计算并输出结果,否则转换VSC控制方式,返回步骤2。 为验证本文所提潮流计算方法的正确性和灵活性,在VC++6.0软件上编写了相应的计算机程序,对修改的IEEE 14节点直流配电系统进行潮流计算和分析,算例系统结构如图3所示。 图3 修改的IEEE 14节点直流算例系统Fig.3 Modified IEEE 14-node DC example system 网络中包含辐射网和环网,1~5号节点为10 kV直流电压等级,6~14号节点为1 kV直流电压等级,高压直流配电网与低压直流配电网通过2台DC/DC变换器相连。共连接3台VSC,其中VSC1和VSC2与交流电网相连,VSC3与交流分布式电源相连。系统的基准容量值取SB=1 MW,基准电压值取各节点的额定电压值。节点有功负荷(标幺值)已用红色数字标出。考虑到换流器的直流侧不同控制方式,根据直流配电网的控制策略分3个场景进行潮流测试。各场景下3台VSC交流侧控制与计算参数均相同,定交流母线电压控制Us=1.0(标幺值),电阻Rc=0.000 2(标幺值),电抗Xc=0.001(标幺值),损耗系数a=0.001 1(标幺值),b=0.000 9(标幺值),c=0.004(标幺值)。 VSC1作为主换流器,采用定直流电压控制,电压控制值为1.0 (标幺值)。VSC2和VSC3为从换流器,采用定有功控制,有功控制值分别为0.7 MW和0.2 MW。潮流收敛精度与环网收敛精度均为10-6,经过6次迭代潮流收敛,计算的节点电压值如表1所示,换流器传输有功功率及损耗见附录A表A1。 表1中,15,16和17号节点为程序通过自动搜索所生成的开环虚拟节点,15和16号节点电压与2号节点电压相同,17号节点电压与6号节点电压相同,说明2和6号节点为实际开环节点,开环点(2,15),(2,16)和(6,17)分别对应环网2-3-4-2,2-3-4-5-2和6-13-12-6。由附录A表A1可知,VSC的损耗Ploss比换流变压器和换流电抗器的损耗Pz要大很多,潮流计算中不可忽略。 表1 场景1和场景2各节点电压Table 1 Node voltage at scenario 1 and scenario 2 在场景1的基础上,考虑主换流器的功率约束,设置VSC1的有功功率上下限为±1.2 MW,VSC2作为后备换流器,电压裕度值设为1%,即UdcrefH=10.1 kV,UdcrefL=9.9 kV。为使主换流器达到功率限值,VSC3有功功率控制值设为0,退出运行。潮流计算的节点电压值如表1所示,换流器传输有功功率见附录A表A2。 由表1和附录A表A2可知,VSC1传输有功功率为1.2 MW,所连1号节点电压低于1.0(标幺值),而VSC2传输有功功率大于0.7 MW,所连3号节点电压为9.9 kV,说明VSC控制方式已经发生转换。VSC1转为定有功控制,VSC2转为定直流电压控制,平衡节点由1号节点转为3号节点。15号节点电压与3号节点电压相同,说明开环点也发生了改变,这是由于平衡节点的转移,程序对网络结构进行了重新搜索。 VSC1和VSC2采用有功功率—电压下垂控制,二者设置相同的参数,参考电压Udcref=10 kV,参考有功功率Pdcref=0.7 MW,下垂系数K=0.04(标幺值),VSC3采用定有功功率控制,有功控制值为0.2 MW。此场景下直流系统中无定电压节点,分别以VSC1和VSC2所在节点作为平衡节点进行潮流计算,对结果进行比较分析。平衡节点电压修正的收敛精度设为10-4,单次潮流收敛精度同场景1。单次潮流计算均经过7次迭代收敛。计算的节点电压值如表2所示,换流器传输有功功率见附录A表A3。 由表2和附录A表A3可知,两次潮流计算的各节点电压相对误差均小于0.001%,并且VSC1和VSC2的有功功率和电压均符合下垂特性方程,从而验证了算法的正确性。计算的VSC1和VSC2的实际有功功率高于设定的参考值,这是因为系统总的负荷功率大于设定的换流器总的有功功率,为维持直流系统电压稳定,换流器根据自身的下垂特性增加传输的有功功率,使系统达到新的平衡点。 表2 场景3各节点电压Table 2 Node voltage at scenario 3 算法性能的相关数据见附录A表A4,表中场景1的环网电压差为2号开环节点与对应15号虚拟节点之间的电压差,场景3的环网电压差为首次单次潮流计算中2号和15号节点之间的电压差,场景3的下垂节点电压差为首次单次潮流计算中3号节点的迭代电压差。由数据可知,场景1经过4次迭代即达到环网的收敛精度要求,而场景3需要5次,这是因为下垂节点的存在使得算法单次迭代所计算的修正功率误差有所增大,且对下垂节点的功率修正导致算法的迭代次数和计算时间都有所增加。 1)利用节点关联矩阵对网络结构进行自动搜索和自动开环处理,平衡节点发生转移时可在不改变节点和支路编号的情况下,通过自动搜索重新确定各节点的父子关系,保证了程序的连续性,提高了效率。 2)建立了环网和下垂节点的统一功率修正矩阵,提出了针对环网和下垂节点的统一功率修正方法,实现了对VSC下垂控制的计算。 3)考虑了VSC的功率限制及其控制方式的转换,对不同控制策略下的直流电网算例进行潮流计算,结果表明算法适用于直流配电网的典型控制策略,验证了算法的灵活性。 4)本文对潮流算法的改进重点考虑了VSC的直流侧控制方式,而简化了对DC/DC变换器模型的处理。实际直流电网中DC/DC变换器也是重要的潮流控制设备,后续研究可进一步考虑DC/DC变换器的潮流控制方式,扩大算法的适用性。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 参 考 文 献 [1] 顾伟,薛帅,王勇,等.基于有限时间一致性的直流微电网分布式协同控制[J].电力系统自动化,2016,40(24):49-55.DOI:10.7500/AEPS20160216006. GU Wei, XUE Shuai, WANG Yong, et al. Finite-time consensus based distributed cooperative control for DC microgrids[J]. Automation of Electric Power Systems, 2016, 40(24): 49-55. DOI: 10.7500/AEPS20160216006. [2] 李霞林,郭力,王成山,等.直流微电网关键技术研究综述[J].中国电机工程学报,2016,36(1):2-17. LI Xialin, GUO Li, WANG Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Proceedings of the CSEE, 2016, 36(1): 2-17. [3] 宋强,赵彪,刘文华,等.智能直流配电网研究综述[J].中国电机工程学报,2013,33(25):9-19. SONG Qiang, ZHAO Biao, LIU Wenhua, et al. An overview of research on smart DC distribution power network[J]. Proceedings of the CSEE, 2013, 33(25): 9-19. [4] LIU T, LI G, HAN B, et al. Research on the topology of DC distribution network and the influence of distributed generations access to the network[C]// 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), November 26-29, 2015, Changsha, China. [5] 季一润,袁志昌,赵剑锋,等.一种适用于柔性直流配电网的电压控制策略[J].中国电机工程学报,2016,36(2):335-341. JI Yirun, YUAN Zhichang, ZHAO Jianfeng, et al. A suitable voltage control strategy for DC distribution power network[J]. Proceedings of the CSEE, 2016, 36(2): 335-341. [6] YANG M, XIE D, ZHU H, et al. Architectures and control for multi-terminal DC (MTDC) distribution network review[C]// 11th IET International Conference on AC and DC Power Transmission, February 10-12, 2015, Birmingham, UK. [7] 刘天皓.直流配电网电压控制策略研究[D].北京:华北电力大学,2016. [8] 李亚楼,穆清,安宁,等.直流电网模型和仿真的发展与挑战[J].电力系统自动化,2014,38(4):127-135.DOI:10.7500/AEPS20130422006. LI Yalou, MU Qing, AN Ning, et al. Development and challenge of modeling and simulation of DC grid[J]. Automation of Eletric Power Systems, 2014, 38(4): 127-135. DOI: 10.7500/AEPS20130422006. [9] HAILU T, MACKAY L, GAJIC M, et al. From voltage stiff to voltage weak DC distribution grid: opportunities and challenges[C]// IEEE 2nd Annual Southern Power Electronics Conference (SPEC), December 5-8, 2016, Auckland, New Zealand. [10] RODRIGUEZ P, ROUZBEHI K. Multi-terminal DC grids: challenges and prospects[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(4): 515-523. [11] 陈谦,唐国庆,王浔.多端VSC-HVDC系统交直流潮流计算[J].电力自动化设备,2005,25(6):1-6. CHEN Qian, TANG Guoqing, WANG Xun. AC-DC power flow algorithm for multi-terminal VSC-HVDC systems[J]. Electric Power Automation Equipment, 2005, 25(6): 1-6. [12] 季聪,卫志农,孙国强,等.基于自动微分技术的VSC-HVDC潮流计算[J].电力系统及其自动化学报,2013,25(2):1-6. JI Cong, WEI Zhinong, SUN Guoqiang, et al. Power flow calculation of the AC-DC system with VSC-HVDC based on automatic differentiation[J]. Proceedings of the CSU-EPSA, 2013, 25(2): 1-6. [13] DOU J, ZHANG B, CHAI R, et al. Unified iterative power flow algorithm of AC/DC networks incorporating hybrid HVDC[C]// IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), June 7-10, 2016, Florence, Italy. [14] AHMED H M A, ELTANTAWY A B, SALAMA M. A generalized approach to the load flow analysis of AC-DC hybrid distribution systems[J]. IEEE Transactions on Power Systems, 2018, 33(2): 2117-2127. [15] 薛振宇,房大中.基于双向迭代的交直流互联电力系统潮流计算[J].电力系统自动化,2013,37(5):61-67. XUE Zhenyu, FANG Dazhong. A power flow calculation algorithm for AC/DC interconnected power systems based on bi-directional iteration[J]. Automation of Electric Power Systems, 2013, 37(5): 61-67. [16] 王成山,孙充勃,彭克,等.微电网交直流混合潮流算法研究[J].中国电机工程学报,2013,33(4):8-15. WANG Chengshan, SUN Chongbo, PENG Ke, et al. Study on AC-DC hybrid power flow algorithm for microgrid[J]. Proceedings of the CSEE, 2013, 33(4): 8-15. [17] 杨舒婷,王承民,李骄阳,等.直流配电网的集中-分布式控制策略[J].电网技术,2016,40(10):3073-3080. YANG Shuting, WANG Chengmin, LI Jiaoyang, et al. Centralized-distributed control strategies in DC distribution[J]. Power System Technology, 2016, 40(10): 3073-3080.3.2 环网和下垂节点的功率修正

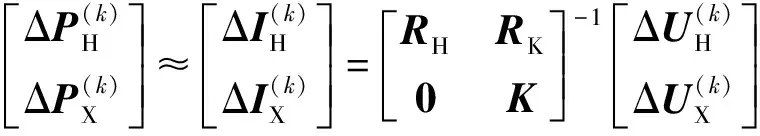
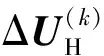

3.3 直流电网中无定电压控制节点的处理方法
3.4 VSC功率越限校验
3.5 潮流计算步骤
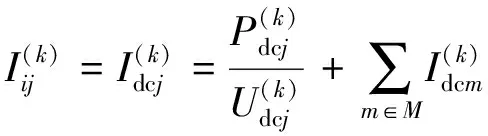
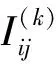
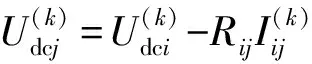
4 算例分析
4.1 算例系统

4.2 场景1:主从控制
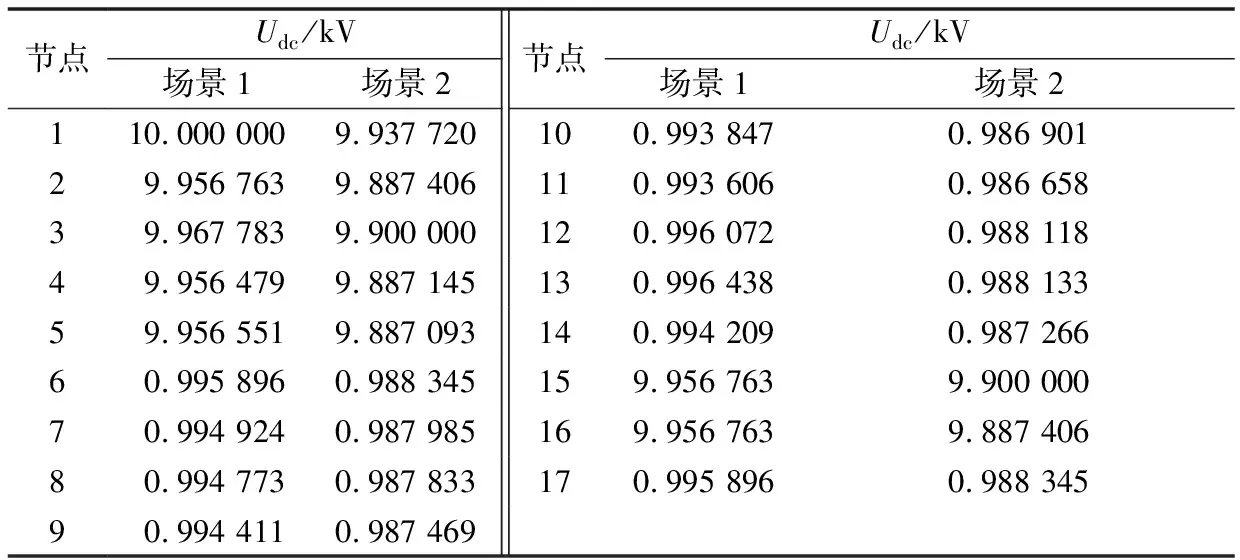
4.3 场景2:电压裕度控制
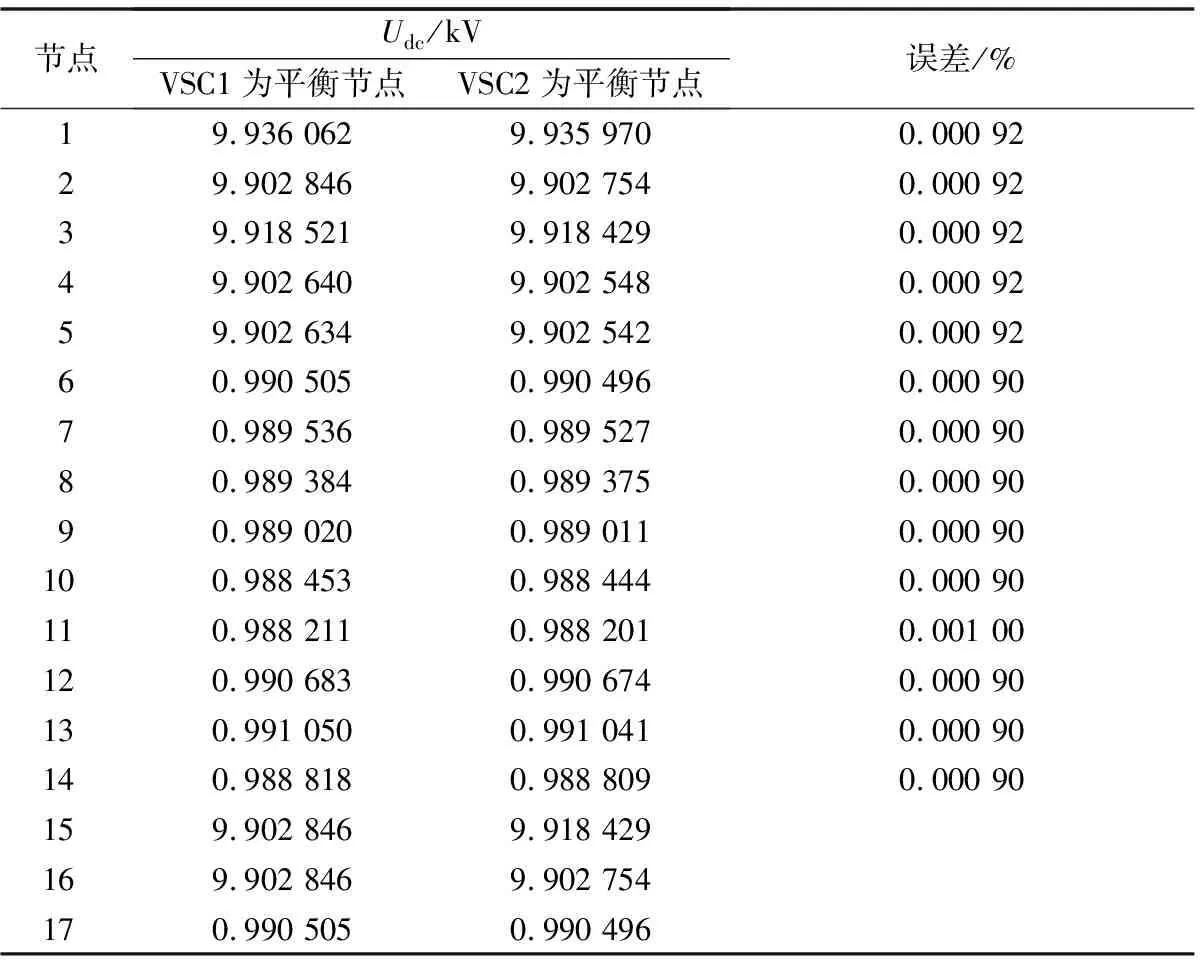
4.4 场景3:电压斜率控制
5 结论

