基于长短期记忆网络的售电量预测模型研究

方志强， 王晓辉， 夏 通

( 国网浙江省电力有限公司丽水供电公司，浙江 丽水 323050)

0 引言

随着国家经济的高速发展，电力事业也处在大力发展的阶段，准确地对售电量进行预测具有重要意义，一方面供电企业可以据此调整未来供电量，优化供电结构，提高电力系统运行的安全性；另一方面，售电量作为经济发展的晴雨表，能帮助政府和供电公司了解本地区的经济发展情况，进而为管理者对售电定价、用电策略等决策[1]提供数据支撑，并有助于统筹所有行业的发展规划。

根据售电量历史数据对未来售电量进行预测，在本质上可以归纳为时间序列预测问题。时间序列是指将某种统计指标在不同时刻所表示的数值按照其发生的先后顺序排列而成的序列，而时间序列数据则是时间序列所反应的实际数据。影响售电量的因素是多样的，不仅仅在时间轴上与售电量自身因素有关，还与季节、气温、气候、经济发展、周末情况、节假日情况等因素有关，因此该预测问题是多条件的时间序列预测问题。

基于历史时间序列数据对未来数据进行预测的问题已经得到了国内外广泛的研究。较早的方法是英国统计学家YULE U提出的自回归模型(AR)，在该模型基础上，WALKER G T提出了滑动平均模型(MA)以及自回归滑动模型(ARMA)。由于ARMA模型无法很好地在非平稳数据上进行拟合，BOX和JENKINS提出了自回归积分滑动模型(ARIMA)[2]。文献[3—5]给出了基于ARIMA模型的售电量预测方法，通过将售电量序列看成一个随机序列，运用一个数学模型来描述，并基于该模型预测未来的售电量数据。

除了经典的自回归模型，THISSEN U和GUI B提出了支持向量机的时间序列数据预测方法[6-7]，程海涛等[8]提出一种支持向量机结合X11季节调整方法用于短期电力负荷预测。宋晓华等[9]提出一种基于改进GM(1,1)和支持向量机的优化组合预测模型，该模型在对比较复杂的序列数据进行预测时，在性能上要高于ARIMA模型。张魁等[10]利用大数据技术通过比对GDP和电量负荷的增长趋势，并且引用政策因素对电量负荷进行预测。此外，由于售电量数据产生通常都是非线性的，受多种因素影响，线性模型通常无法得到较高的预测精度，而基于人工神经网络(ANNs)的售电量预测方法[11-13]能够执行非线性模型，进一步提高了预测的准确性。

深度学习是近几年提出的一种非常有效的自动提取数据特征的有效方法[14]，例如循环神经网络(RNNs)模型[15]是一种适合于处理序列数据的模型，它基于循环的网络结构能够利用序列数据本身的序列信息，发现序列的内在规律和特征，如将RNNs模型应用于股票预测[16]、轨迹位置预测[17]、语音识别[18]、自然语言处理[19-20]等领域。

长短期记忆网络(long-short term memory，LSTM)是一种改进的RNNs模型，它通过修改RNNs 结构中的隐藏层神经元，解决了RNNs无法有效地利用长间隔序列的问题。为了提高售电量数据的预测准确性，本文提出一种基于长短期记忆网络的售电量预测模型，该模型通过自动学习售电量历史数据以及影响因素数据特征，能够得到更好地预测准确度。

1 深度学习基本模型

循环神经网络 (RNNs)在20世纪80年代被提出，与传统人工神经网络相比，其循环的网络结构使其可以充分利用序列数据本身的序列信息。

传统的人工神经网络中各个神经元的输入与输出都是相互独立的，不直接作用于彼此，且保持层间全连接，层内无连接。而在 RNNs 中，神经元在当前时刻的输出可以在下一时刻作用于其自身，这就使得循环神经网络可以利用历史输入信息，而不仅仅只是根据当前时刻的输入数据来更新权重，如图1所示，横向上 RNNs 按时间步长展开，其各时间步共享权重。

图1 RNNs网络结构Fig.1 Structure of RNNs network

(1)

(2)

式中：i表示输入特征向量的维度；k表示输出特征向量维度；h表示隐层；h′表示前一时间步的隐层；H表示总隐层单元数；φ表示激活函数；W1表示输入层到隐藏层的权重；W2表示自循环层权重；W3表示隐藏层到输出层的权重。

RNNs使用基于时间的反向传播学习算法 (BPTT)[21]进行训练，反向传播时将网络按时间展开，误差将按时间顺序从最后一个时刻往前进行传播， 最后进行权重更新。

因为RNNs特殊的网络结构，使得其可以充分学习到序列数据中前后数据的关联关系，所以 RNNs被广泛地应用于时间序列类问题。

2 长短期记忆网络

由于RNNs在训练时采用BPTT反向传播算法，当遇到长间隔的序列在反向传播通过链式法则求梯度时会出现梯度消失的现象[22]，且梯度消失现象随着时间跨度越长越严重，这使得 RNNs 在针对长范围的序列时难以有效地进行训练。

为了解决 RNNs 无法有效地利用长间隔序列问题，HOCHREITER S和SCHMIDHUBER J修改了RNNs 结构中的隐藏层神经元，将其设计成了一种被称为长短期记忆网络(long-short term memory，LSTM)的记忆单元结构[23-24]，通过3种门结构: 遗忘门,输入门和输出门来控制神经元对历史信息的记忆，如图2所示,t时刻的计算过程如下。

图2 LSTM记忆单元Fig.2 LSTM memory cell

(3)

ft=sigmoid(Wxfxt+Whfht-1+Wcfct+bf)

(4)

ct=ftct-1+ittanh(Wxcxt+Whcht-1+bc)

(5)

ot=sigmoid(Wxoxt+Whoht-1+Wcoct+bo)

(6)

ht=ottanh(ct)

(7)

式中 ：i,f,o分别表示输入门，遗忘门，输出门；c表示记忆单元；h表示隐层输出，其下标表示时刻t；W表示连接权重，其下标表示权重关联项，例如Wxi表示从输入层到输入门的连接权重，b为偏置项。根据i,f,o在[0, 1]范围的取值，来控制历史信息通过门结构的比例。tanh、sigmoid则为激活函数。

3 基于LSTM的售电量预测模型

3.1 售电量与影响因素相关性

由于售电量数据涉及多个产业，每个产业又包括多个行业，每个行业在售电量方面都有各自的影响因素，故需要对各个行业进行分类处理。

使用Pearson相关系数[25]作为每个行业的售电量数据与其他影响因素数据特征的相关性的评价依据，其计算方法如下：

(8)

式中：r表示Pearson相关系数,取值范围为[-1,1]，其中0表示不相关，其值越接近1则正相关性越大，越接近-1则是负相关性越大；x和y为两个数据特征变量；Cov(x,y)表示协方差；σx，σy表示标准差。

通过以上计算结果可以知道两个数据特征变量之间是否相关，如售电量数据与气温数据的相关性，售电量数据与GDP数据的相关性,售电量数据与投资数据的相关性，售电量数据与日期数据的相关性等。对于不相关的影响因素或相关性弱的影响因素则予以排除。

3.2 行业售电量聚类

由于每个行业的售电量情况不同，根据每个行业售电量单独训练模型，将使训练过程过于复杂且训练模型数量众多。故本文提出先根据Pearson相关系数使用K-means算法对行业进行聚类，将售电量特征相似的行业聚为一类，这将大幅减少模型的数量。聚类之后得到若干个簇，每个簇包含了若干行业，同一簇中行业的售电量数据对某些数据特征具有一定的相似性，聚类算法如下：

输入：售电量序列数据，Pearson相关系数集合D={x1,x2,…,xm}，xi表示第i个行业的相关系数向量，其中的每一维表示与售电量相关的影响因素，m表示行业个数，聚类簇数是k；

输出：簇划分R；

步骤：从相关系数集合D中随机选取k个行业的相关系数向量作为初始均值向量μ={μ1,μ2,…μk}，其中μi是第i个行业的相关系数向量。

(1) do

(2)R=Φ

(3) forj= 1,2,…,mdo

(4) 计算xj与μi的距离，根据距离最近的均值向量确定xj的簇划分

(5) end for

(6) fori=1,2,3,…,kdo

(7) 计算新均值向量μi′

(8) 如果μi′!=μi则更新μi否则保持不变

(9) while(μ不再更新)

3.3 数据归一化处理

由于售电量数值与影响因素的数值相差较大，故必须对这些数据进行归一化处理，将各类数值缩放到同一尺度，缩放公式如下：

(9)

式中：x为每一类数据的原始数值；xmin为每一类数据的最小值；xmax为每一类数据的最大值，x*为该类数据计算得到的数值。

3.4 多条件售电量预测模型

设售电量时间序列数据为：

X=(x1,x2,…,xt-1,xt)

(10)

式中：xt是t时刻的售电量，则售电量预测问题即是根据已知时间序列数据X，求得xt+1时刻的最大似然估计P(x):

(11)

由于售电量不仅仅受自身历史数据的影响，也受其他各种相关因素的影响，即是多条件时间序列问题。由此，公式(8)变成如下形式：

(12)

式中：xt表示t时刻的售电量;ht表示t时刻额外的影响因素。

公式(11)与公式(12)是售电量预测的目标，通过在已知历史售电量和外部影响因素数据求得下一日的售电量的条件概率P(xy)，该条件概率通过LSTM模型进行拟合，如上公式(1—7)给出t时刻的计算过程，其中公式(6)为模型输出，即售电量预测数值。由于LSTM存在门结构和记忆单元可以控制历史信息在神经网络中的传递，从而使得本文模型可以充分的利用历史售电量数据，此外施加的外部影响因素数据也会对售电量预测模型产生影响。

3.5 售电量预测过程

图3给出了基于长短期记忆网络的售电量预测的过程图。该过程以售电量数据和外部影响因素数据作为输入。首先分别计算各个影响因素与各个行业售电量的相关系数，并且以行业数作为行数，以影响因素数作为列数，构建该行业聚类特征矩阵：

(13)

图3 售电量预测过程Fig.3 Sales forecasting process

其次，根据聚类结果划分原始售电量数据集，将相似的行业的售电量数据划分为同一个子集，同时对同一子集中的所有售电量数据按日期进行累加得到该子集的日总售电量数据。

最后，根据以上子集划分情况，分别训练与划分数量对应数量的模型。在预测阶段，对每个簇的行业总售电量进行独立预测，每个模型将输出相应簇的售电量预测数值，最终将多个模型的预测结果进行累加得到总的日售电量预测结果。

4 实验与分析

本文结合实际售电量数据对所提出的预测方法进行了验证。数据来自某市总计10个电力部门共106个行业的日售电量数据，总数据集大小为178 793条，106个行业的总售电量如图4所示，时间跨度为2015年1月至2017年5月。将2015年1月1日至2016年12月31日的数据作为训练数据集，将2017年1月1日至2017年5月31日的数据作为测试数据集。以15 d为预测单位，即根据历史售电量信息每次预测未来15 d的售电量的值。

图4 某市106个行业总售电量Fig.4 A city 106 total sales of electricity industry

同时考虑到不同行业所受影响因素不同，初步选取的影响因素包括：日最高气温，日最低气温，节假日情况，周末情况，季度，每月中的第几天，每年中的第几天，周数，每周中的第几天，GDP，地区投资数据。

将以上影响因素分别与售电量数据计算Pearson相关系数，并执行K-means算法进行聚类，图5给出通过t-SNE算法将聚类结果进行可视化的聚类结果图，t-SNE算法将数据从高维空间映射至二维空间中，通过横轴和纵轴指示数据点在二维空间中的位置并展示数据点与数据点间的距离。

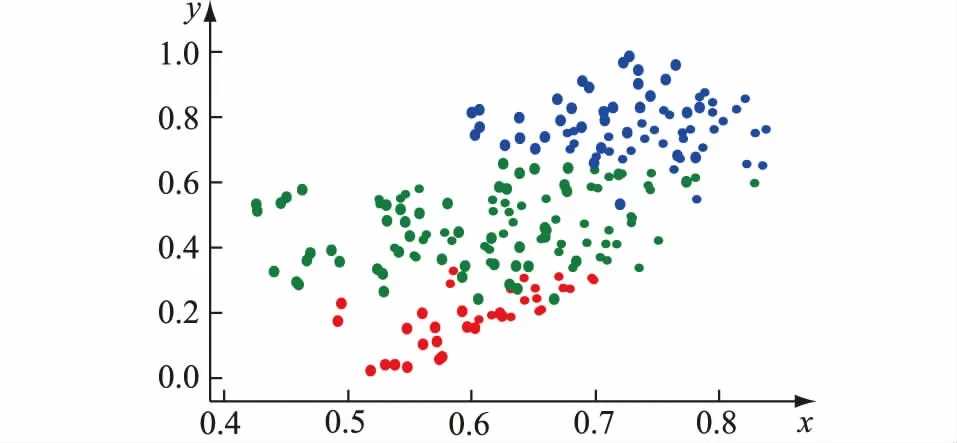
图5 聚类结果可视化Fig.5 Visualization of clustering results

实验环境为一台GPU服务器，CPU为Intel Xeon E5—2680 v4，内存为64 GB，GPU为Nvidia TiTan XP，软件平台为Google Tensorflow。选择BP神经网络预测模型[26]与本文提出的预测模型进行比较，该模型具有较好预测准确性，以突出本文方法的优势。

为了评估预测值与真实值的误差，本文选用均方误差(mean squared error，MSE)作为评价指标，同时MSE也作为LSTM售电量预测模型的目标函数，目标函数如下：

(14)

本文使用3层LSTM网络对售电量数据进行预测，在每层LSTM间使用dropout抑制模型过拟合现象。使用如上所示的训练集，在本实验环境中对模型进行训练，如图6所示，经过200次迭代模型即可收敛，训练总计用时8 min左右。

图6 模型收敛曲线Fig.6 Convergence curves for LSTM model

通过行业聚类将数据集按行业进行划分，预测阶段也将按照聚类结果分别进行预测，图7给出了LSTM模型与BP神经网络的预测结果，其中LSTM模型的预测结果为根据子集划分情况分别预测后累加而成的总售电量预测。从图7中可以看到LSTM网络预测模型相比于BP神经网络更贴近真实值，预测误差较小，即使数据出现突降也能很好地进行预测。LSTM网络与BP神经网络的MSE值分别为0.009 2与0.028 51，平均误差分别为2.1%与15.8%，由此可发现基于LSTM的售电量预测模型相比BP神经网络模型在预测精度上具有较大的提升。

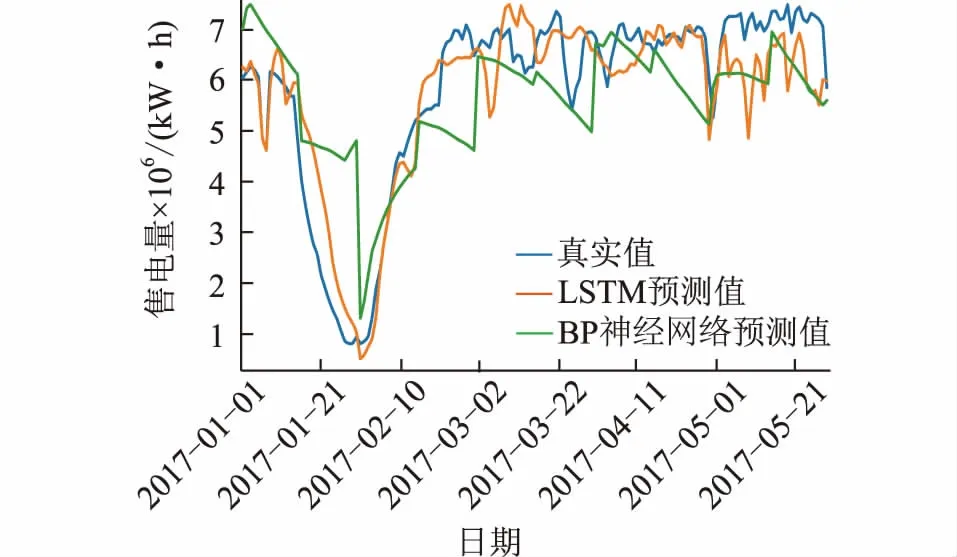
图7 售电量预测结果对比Fig.7 Comparison figure of the result of electricity sale forecast

5 结语

为了提高售电量预测的准确性，本文提出了一种基于长短期记忆网络的售电量预测方法，通过分析售电量数据及其影响因素的相关性，根据各个行业的数据特征将相似的行业进行聚类，并根据聚类结果训练长短期记忆网络，自动学习售电量数据以及相关影响因素的数据特征，通过所设计的多条件时间序列预测模型得到更好的售电量预测结果。

参考文献：

[1] 吴 桥, 卢树峰, 杨世海,等. 需求侧响应条件下的家庭用电管理研究[J]. 电力工程技术, 2016, 35(5):28-31.

WU Qiao, LU Shufeng, YANG Shihai, et al. Research on home energy management under the condition of demand-side response[J]. Electric Power Engineering Technology, 2016,35(5):28-31.

[2] BOX G E P, JENKINS G M. Time series analysis: forecasting and control[J]. Journal of the American Statistical Association, 1970, 68(342):199-201.

[3] 颜 伟,程 超,薛 斌,等. 结合X12乘法模型和ARIMA模型的月售电量预测方法[J]. 电力系统及其自动化学报,2016,28(5):74-80.

YAN Wei, CHENG Chao, XUE Bin, et al. Forecasting for monthly electricity consumption using X12 multiplication method and ARIMA model[J]. Proceedings of the CSU-EPSA,2016,28(5):74-80.

[4] 樊 娇,冯 昊,牛东晓,等. 基于小波分析和GM-ARIMA模型的月度售电量预测[J]. 华北电力大学学报(自然科学版),2015,42(4):101-105.

FAN Jiao, FENG Hao, NIU Dongxiao,et al. Monthly electricity sales forecast based on wavelet analysis[J]. Journal of North China Electric Power University(Natural Science Edition),2015,42(4):101-105.

[5] 崔和瑞,王 娣. 基于季节ARIMA模型的华北电网售电量预测研究[J]. 华东电力,2009,37(1):70-72.

CUI Herui, WANG Di. Study of electricity sales forecasting for North China Power Grid based on seasonal ARIMA model[J]. East China Electric Power, 2009,37(1):70-72.

[6] THISSEN U, VAN B R, DE W A, et al. Using support vector machines for time series prediction[J]. Chemometrics and Intelligent Laboratory Systems, 2003, 69(1):35-49.

[7] GUI B, WEI X, SHEN Q, et al. Financial time series forecasting using support vector machine[C]∥Tenth International Conference on Computational Intelligence and Security. 2015: 39-43.

[8] 程海涛. 支持向量机结合X11季节调整方法用于短期电力负荷预测[D]. 甘肃：兰州大学,2011.

CHENG Haitao. X11 seasonal adjustment combined with SVM for short-term electric load forecasting[D]. Gansu: Lanzhou University,2011.

[9] 宋晓华, 祖丕娥, 伊 静,等. 基于改进GM(1,1)和SVM的长期电量优化组合预测模型[J]. 中南大学学报(自然科学版), 2012, 43(5):1803-1807.

SONG Xiaohua, ZU Pi’e, YI Jing, et al. An optimally combined forecast model for long-term power demand based on improved grey and SVM model[J]. Journal of Central South University(Science and Technology), 2012, 43(5):1803-1807.

[10] 张 魁, 王亚明, 刘 明,等. 基于大数据及智能算法的连云港电量负荷预测研究[J]. 电力工程技术, 2016, 35(3):49-52.

ZHANG Kui, WANG Yaming, LIU Ming, et al. Research on electricity consumption and load prediction of Lianyungang based on big data and intelligent algorithm[J]. Electric Power Engineering Technology, 2016,35(3):49-52.

[11] 张 喆, 吴知非, 禹建丽. 电力电量预测的神经网络方法[J]. 统计与决策, 2008(4):156-157.

ZHANG Zhe, WU Zhifei, YU Jianli. Neural network method for power forecasting[J]. Statistics and Decision, 2008(4):156-157.

[12] 衣 智. 人工神经网络在电力预测中的应用[D]. 天津： 天津大学, 2002.

YI Zhi. Application of artificial neural network in power forecasting[D]. Tianjin :Tianjin University,2002.

[13] 冯冬青, 李卫帅. 基于GA-BP神经网络的电池剩余电量的预测[J]. 计算机仿真, 2011, 28(12):323-326.

FENG Dongqing, LI Weishuai.Prediction of residual capacity for battery based on GA-BP neural network[J]. Computer Simulation, 2011, 28(12):323-326.

[14] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553):436-444.

[15] CONNOR J T, MARTIN R D, ATLAS L E. Recurrent neural networks and robust time series prediction[J]. IEEE Transactions on Neural Networks, 1994, 5(2):240-54.

[16] 俞福福. 基于神经网络的股票预测[D]. 哈尔滨：哈尔滨工业大学, 2016.

YU Fufu. Stock prediction based on neural netwok[D]. Harbin：Harbin Institute of Technology,2016.

[17] 李幸超. 基于循环神经网络的轨迹位置预测技术研究[D]. 杭州：浙江大学, 2016.

LI Xinchao. The research of location prediction based on recurrent neural network[D]. Hangzhou: Zhejiang University,2016.

[18] 滕 云, 贺春林, 岳 淼. 基于神经网络的语音识别研究[J]. 重庆师范大学学报(自然科学版), 2010, 27(4):73-76.

TENG Yun, HE Chunlin, YUE Miao. Research on speech recognition based on neural networks[J]. Journal of Chongqing Normal University(Natural Science), 2010, 27(4):73-76.

[19] GRAVES A, MOHAMED A, HINTON G. Speech recognition with deep recurrent neural networks[C]∥Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on. IEEE, 2013: 6645-6649.

[20] MIAO Y, GOWAYYED M, METZE F. EESEN: End-to-end speech recognition using deep RNN models and WFST-based decoding[C]∥Automatic Speech Recognition and Understanding. IEEE, 2016:167-174.

[21] RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533.

[22] BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Tran-sactions on Neural Networks, 1994, 5(2): 157-166.

[23] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation. 1997, 9(8):1735-1780.

[24] GERS F A, SCHRAUDOLPH N N, SCHMIDHUBER J. Learning precise timing with LSTM recurrent networks[J]. Journal of Machine Learning Research, 2002, 3(8): 115-143.

[25] 陈功平,王 红. 改进Pearson相关系数的个性化推荐算法[J]. 山东农业大学学报(自然科学版), 2016, 47(6):940-944.

CHEN Gongping, WANG Hong. A personalized recommendation algorithm on improving pearson correlation coefficient[J]. Journal of Shandong Agricultural Univers, 2016, 47(6):940-944.

[26] 吴 微, 陈维强, 刘 波. 用BP神经网络预测股票市场涨跌[J]. 大连理工大学学报, 2001, 41(1):9-15.

WU Wei, CHEN Weiqiang, LIU Bo. Prediction of ups and downs of stock market by BP neural networks[J]. Journal of Dalian University of Technology, 2001, 41(1):9-15.