基于变目标控制的MMC-HVDC控制策略
夏成军, 刘志江, 杜兆斌
( 华南理工大学电力学院,广东 广州 510641)
0 引言
基于模块化多电平换流器的高压直流输电系统(modular multilevel converter high voltage direct current, MMC-HVDC)具有独立控制有功和无功、无换相失败风险、潮流调配灵活等优点,有利于构筑直流配电网和多端柔性直流输电系统等需要频繁调节潮流的电力网络[1-4]。MMC-HVDC的应用场合决定了其需要良好的控制性能,在保证直流输电系统电压和功率稳定的前提下提高潮流调配的灵活性和抗干扰能力。
文献[5]分析了MMC的电路结构和特性,得到MMC的简化电路模型,指出MMC-HVDC可以使用传统电压源型换流器高压直流输电系统(voltage source converter HVDC ,VSC-HVDC)的双环控制策略。文献[6]建立了换流器三相坐标系和旋转坐标系下的基于端口受控耗散哈密尔顿(port-controlled hamiltonian with Dissipation, PCHD)模型,提出了一种换流器的阻尼分配无源性(interconnection and damping assignment-passivity based, IDA-PB)控制方法,具有良好的动、静态性能和鲁棒性。由于VSC-HVDC系统为非线性系统,文献[7]提出了一种基于反步法的自适应控制以提高VSC-HVDC的动态性能,其考虑了VSC-HVDC系统的非线性和参数的不确定性。文献[8-10]推导出dq同步坐标下的VSC-HVDC连续数学模型,设计了内外环控制,利用前馈补偿来消除换流器模型中d轴和q轴之间的耦合,实现了有功功率和无功功率、直流电压和无功功率的独立控制。文献[11—12]设计了针对VSC-HVDC的模糊自适应PI控制策略,改进了系统动、稳态性能,减少在起始阶段的超调,并在稳态时转为PI控制以避免模糊控制的抖震现象。文献[13]利用平坦系统控制理论建立VSC-HVDC的双环控制系统,其特点是不需要精确的数学模型,系统的适应性更强,有利于提高控制系统的动态性能。
目前国内外研究中,MMC-HVDC大部分都采用经典双环控制策略。双环控制策略结构简单,不依赖精确的数学模型,具有较强的适应性,但存在快速性与超调量的矛盾,且PI环节参数难以整定,无法很好地保证控制系统的鲁棒性、稳定性和快速性。本文根据简化后的MMC-HVDC数学模型和离散的双环控制策略,设计了对应的变目标控制策略,将控制的最终目标值分成多个小目标,使系统在一定时间内无超调快速分步达到指定的目标值,解决快速性和超调量的矛盾,简化系统的双环控制PI参数的整定,并提高了控制系统的鲁棒性。在此基础上,分析了加入变目标控制环节后双环控制PI参数的设置原则,并基于改进的时间误差积分(integrated time and absolute error, ITAE)指标,提出了变目标控制策略调节时间参数的优化方法。在PSCAD/EMTDC仿真平台中搭建三端柔性直流输电模型测试本文设计变目标控制策略的性能。仿真结果表明,加入变目标控制环节可以有效提升MMC-HVDC控制系统直流电压、直流有功功率恢复速度,有效维持系统的稳定运行。
1 MMC-HVDC数学模型和内外环控制
MMC模块由6个桥臂组成,每个桥臂由若干个相同的子模块与阀阻抗L0、电阻R串联组成。在研究MMC-HVDC的外部控制时,子模块可以被认为是一个电压源,MMC等效电路如图1所示。
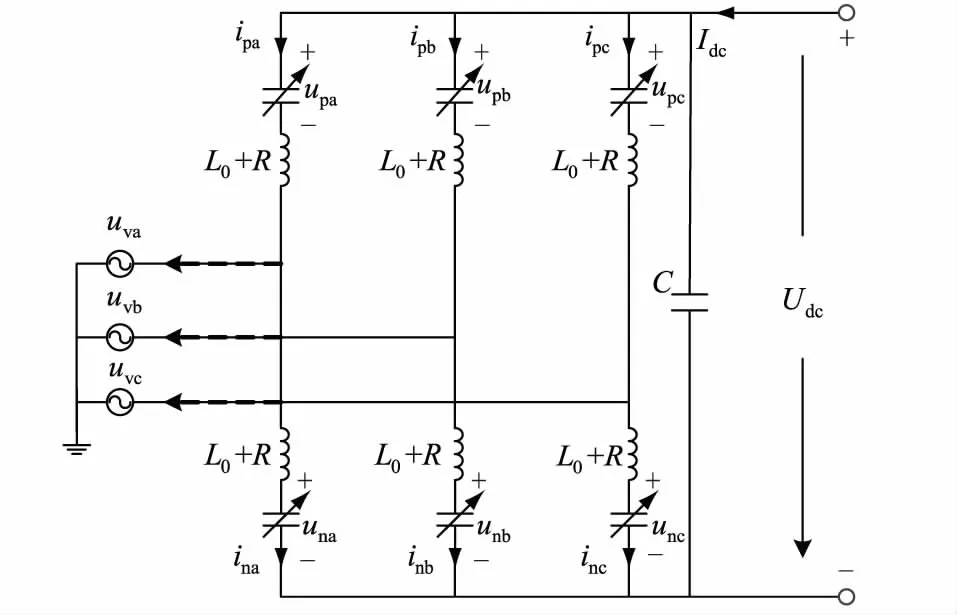
图1 MMC-HVDC一侧系统简化等效电路Fig.1 Simplified equivalent circuit of MMC-HVDC unilateral system
根据MMC-HVDC连续时间数学模型设计的控制器也是连续时间状态控制器,而实际控制器系统通常采用微机控制,其采样有时间间隔,控制器只能根据采样时刻的偏差值计算控制量[14]。为了适应微机控制,对MMC-HVDC连续时间数学模型[5]进行离散化,推导稳态时MMC-HVDC离散数学模型,整流侧的交流侧数学模型:
(1)
(2)
式中:vd、vq,ud、uq,id、iq分别为dq同步旋转坐标系下MMC换流器输出的基波电压向量,交流母线基波电压向量和电流基波向量,ω为系统的角频率,Ts为采样时间。整流侧的直流侧数学模型:
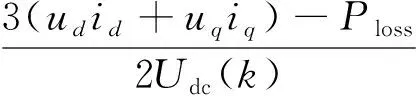
(3)
式中:Icc为直流线路上的电流;Ploss为换流器和变压器损耗之和。
根据式(1)(2)和数字PI控制器的特性,可以设计出基于微机控制的离散电流内环控制策略:
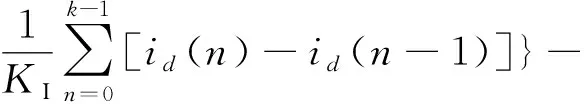
(4)
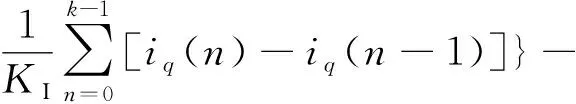
(5)
式中:下标为ref的变量为指令参考值;KP为PI环节的比例环节系数,KI为积分环节系数。id,ref、iq,ref可由外环控制输入得到,vd,ref、vq,ref为阀组控制的参考值。

图2 内环控制的控制框图Fig.2 Control block diagram of inner loop control
外环控制根据有功功率、无功功率以及直流电压的参考值,计算内环电流控制的参考值。多端柔性直流系统正常运行时,各端中必须有一端换流站采用定直流电压控制,用于稳定系统的直流电压,并配合定无功功率控制;其他换流站一般采用定有功功率控制和定无功功率控制。
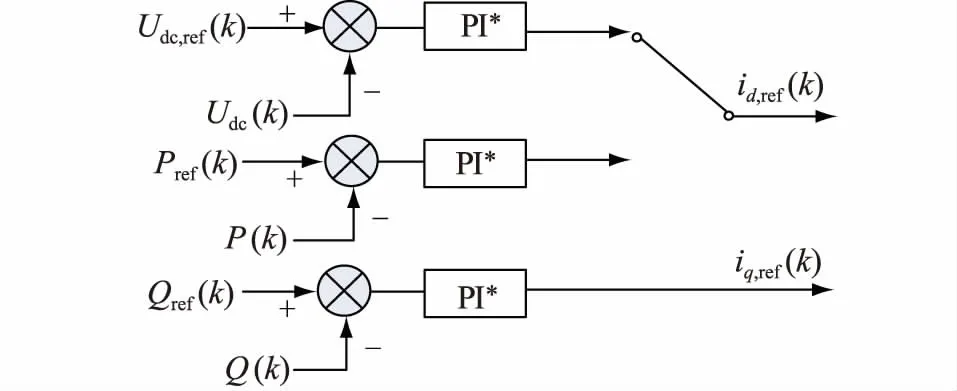
图3 外环控制器控制框图Fig.3 Outer loop controller control block diagram
2 变目标控制策略设计
通过对MMC-HVDC控制系统快速性和超调量之间的矛盾关系研究发现,传统的双环控制系统接收到阶跃信号时,控制系统的输入突变为e=u-v0,但是系统的控制量只能从0开始连续变化,并不能突变。在实际控制过程中,控制效果受系统的执行机构和系统状态的约束,控制的变量限制在一定的范围。在该范围内被控系统能根据控制系统的要求进行调整,超出该范围时控制系统的控制量有可能不是计算值,控制系统进入饱和状态,从而引起超调。
为了解决传统双环控制中快速性与超调量的矛盾,在外环控制目标值的输入后添加变目标控制环节,如图4虚线框内所示。
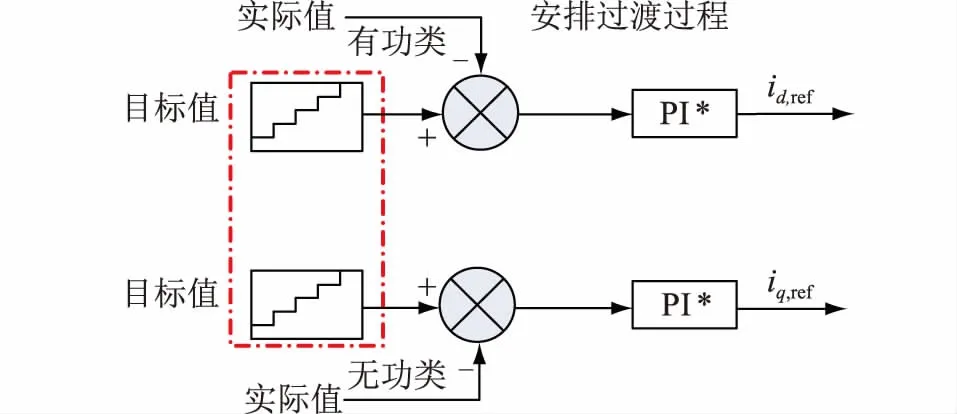
图4 加入变目标控制的双环控制Fig.4 Inner and outer ring control with variable target
本文所加入的变目标控制在被控量初始值和最终目标状态之间,根据系统的承受能力或控制需要,将最终目标值按照一定的曲线分割成多个小目标,使被控量分步达到每一个小目标,最终达到目标值。变目标控制的目的是让系统的调整曲线跟随所设定的变目标曲线,逐步达到目标值,实现快速无超调控制。
变目标控制实际上是一种安排过渡过程的方法。工程上通常把被控制量从开始状态到进入目标值±5%偏差范围内且不再越出的过程称为过渡过程。被控制量的过渡过程一般由被控制对象和控制器决定[15-16]。
变目标控制环节的设计原则:
(1) 变目标控制环节函数需要与系统的阶相匹配,与根据关注的控制参数所得到的简化后控制系统阶数相等[15]。假设MMC-HVDC系统三相平衡,可以将MMC换流器的所有直流电容都化为一个整体[17],并且通过双环控制使d轴和q轴解耦,得到MMC平均值模型等效电路,简化后的MMC-HVDC系统为三阶系统。
(2) 由于变目标控制环节的输出随时间变化,开始时必须有一个非0的加速度。
(3) 当达到调节时间时,变目标控制环节的输出为最终的目标值,且输出值的变化速率为0,以保证加入的变目标环节不影响最终的稳态值。
(4) 加入变目标控制环节后的控制系统在调整时,系统电气量的变化不能超过设备和系统稳定要求的范围。
根据上述原则设计了新增的变目标控制环节的函数,其函数表达式为:
A=U0+V*(Aref-U0)
(6)
(7)
式中:A为加入变目标控制环节后的目标值;U0为控制开始前被控制量的初始值;Aref为最终目标值;V*为一个随时间变化的参数;T为根据系统调节极限设置的调节时间。
变目标控制环节设计流程图如图5所示。

图5 变目标控制环节设计流程Fig.5 Design flow chart of variable target control
3 变目标控制策略对双环控制PI参数的影响
变目标控制环节加入前,系统输入为目标值与实际值之差,加入后,柔性直流输电双环控制的输入被分割成若干小目标,使控制过程中出现多个稳态过程。
对于外环的偏差比例控制,以定直流电压外环控制为例:
Up1(k)=Kp1e1(k)=Kp1[Udc,ref(k)-Udc(k)]
(8)
Up2(k)=Kp2e2(k)=
Kp2{Udc,0+V*[Udc,ref(k)-Udc,0]-Udc(k)}
(9)
式中:Udc,0为控制开始前直流电压的初始值;e1,e2分别为变目标控制环节加入前后的偏差输出值;Up1,Up2分别为变目标控制环节加入前后的偏差比例控制输出值。
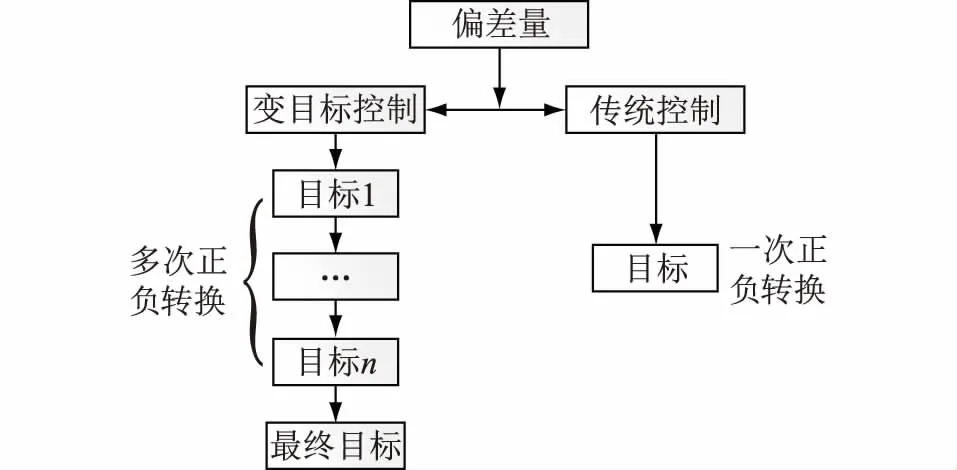
图6 变目标控制与传统控制的偏差比例控制对比Fig.6 Contrast of variable target control =and traditional control
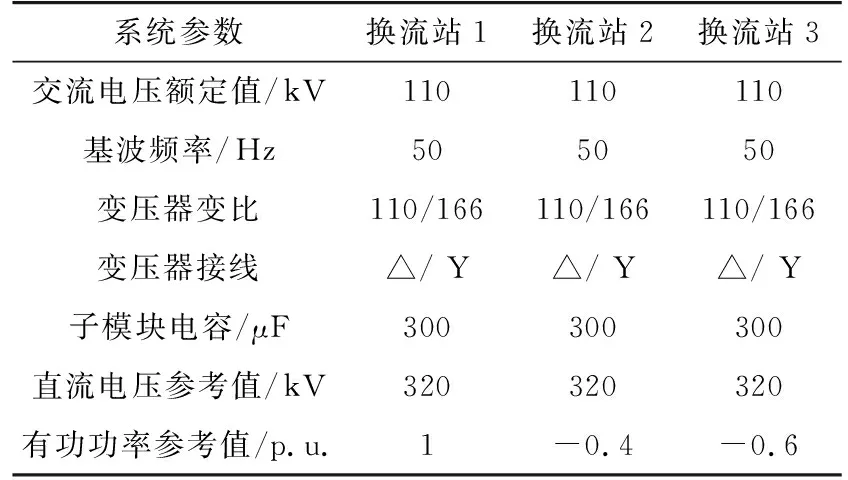
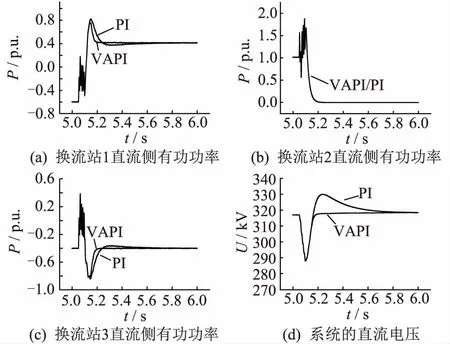
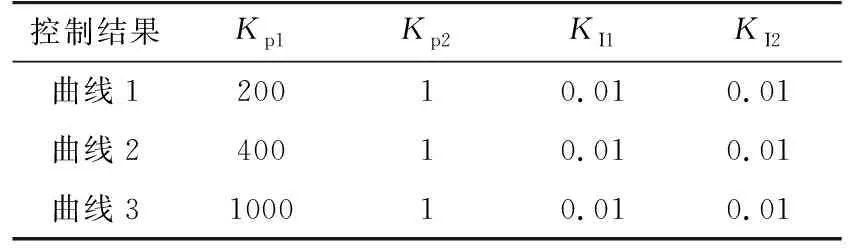
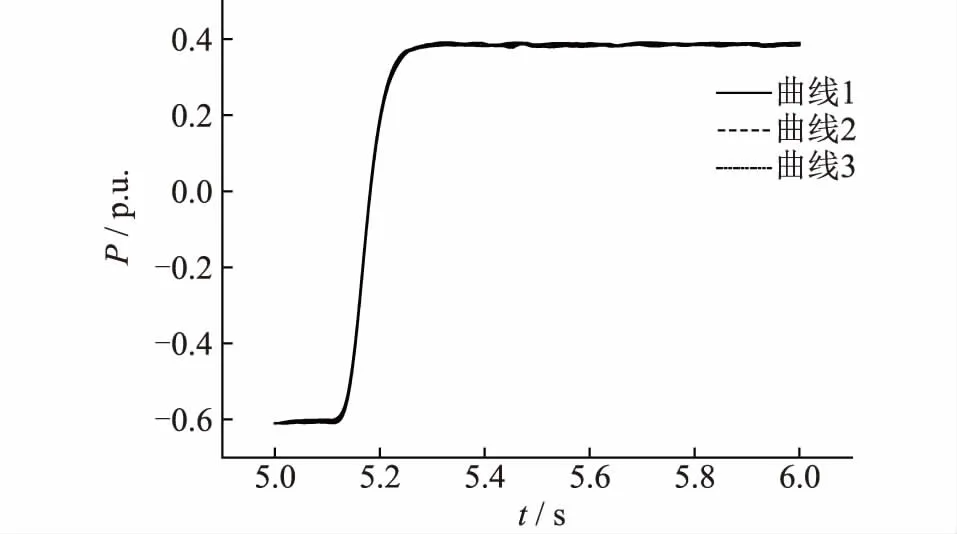
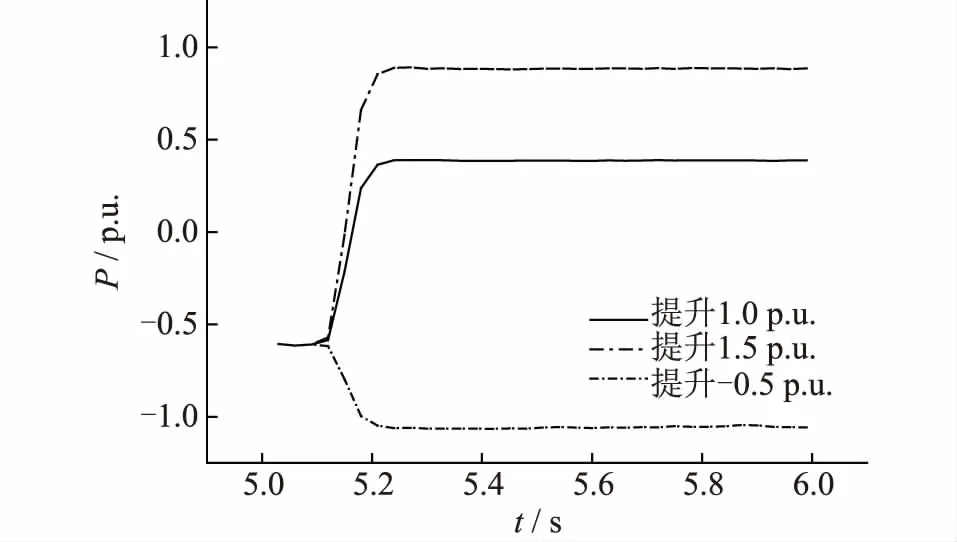
在阶跃信号输入初始时刻,式(9)偏差比例环节输出值远小于式(8)的输出值,即初始力较小,需要采用较大的比例系数给予激励。另外,在每个分段目标的调节过程中,当Udc,0+V*[Udc,ref(k)-Udc,0]>Udc(k)时,为正激励;当Udc,0+V*[Udc,ref(k)-Udc,0] 对于偏差积分环节,以定直流电压控制为例: (10) (11) 式中:UI1、UI2分别变目标控制环节加入前后的偏差积分控制输出值。其中,双环控制PI控制器的积分环节采用积分分离法,即: (12) 式中:ε为积分分离常数。 如图7,当积分输入量(目标值与实际值之差)大于设定的偏差值时,不计入PI控制器的积分累加;当积分输入量小于或等于设定的偏差值时,则计入PI控制器的积分累加。 图7 积分分离法流程Fig.7 Flow chart of integral separation method 对于未加入变目标控制环节的外环控制偏差积分环节,控制开始时,前几个采样周期的积分输入量有可能会超过设定的偏差值,从而被舍弃,仅在积分输入量小于或等于设定的偏差值时才会计入积分累加。变目标控制环节将最终目标分成若干个小目标,每段控制的输入值较小,使得大部分甚至是全部控制过程积分环节都能起作用。加入变目标控制环节后,可以设置较小的积分分离常数ε和积分常数KI。PI控制与变目标控制配合形成温和的积分控制,这样既可以保证系统的调节精度和良好的静态误差消除速率,也可以减少超调量。 综合以上分析,加入变目标控制环节后,双环控制PI环节的比例系数Kp应选择较大,从而获得较大的初始力;积分系数可以选择较小,避免积分饱和。系统的动态误差依靠比例环节消除,稳态误差由积分环节进行消除。加入变目标控制环节后,如果设计的变目标曲线与实际的被控制量曲线重合,实际上就降低了双环控制的PI控制参数对过渡过程的影响,提高了控制系统的鲁棒性和适应性,PI环节参数整定也变得更简单。在系统所能达到的极限内合理设置变目标控制策略的调节时间T和双环控制的PI参数,可以使控制既满足快速性,也没有超调量。 ITAE指标是一种控制系统性能评价指标,具有良好的工程实用性,其含义为时间乘以误差绝对值积分,具体表达式为[19]: (13) 式中:e(t)为被控制量与最终控制目标的误差值;t为时间。 ITAE指标缺少对超调量的考虑,为了更全面地评价控制系统的性能,提出一种改进的ITAE评价指标,加入控制系统的超调量作为参考,将时间乘以误差绝对值积分和超调量的百分比进行加权求和: (14) 式中:σ%为系统的超调量百分比;K1与K2为加权系数。 改进的ITAE指标可以更全面地评价控制系统稳态、动态误差消除的性能,其值越小,则控制系统消除误差越快,性能越优。应用改进的ITAE指标对加入变目标控制环节后的MMC-HVDC控制系统性能进行评价,并将该指标作为整定变目标控制策略调节时间T寻优算法的性能指标函数。 调节时间T为MMC-HVDC变目标控制系统的重要参数之一,对控制系统的性能有重要的影响,为了得到使控制系统性能最优的变目标控制策略调节时间,采用爬山法对调节时间T进行优化。 爬山法是一种最优化算法,一般从一个随机解和随机方向开始寻找最优解,当找到的新解比原有的解更优,则确定为最优解方向,并在此方向继续寻找;当原来的解比新解更优,则更换寻找方向。按照此方法进行优化,得到一个最优解。 基于爬山法原理,对变目标控制策略调节时间T进行优化的具体步骤为: (1) 根据工程经验得出未加入变目标控制环节的控制系统上升时间,作为优化前的初值; (2) 对加入变目标环节后的系统进行阶跃响应试验,根据阶跃响应曲线,计算改进后的ITAE性能指标值; (3) 根据得到的指标值评价MMC-HVDC变目标控制系统的性能优劣,采用爬山法确定最优解的方向,并在调节时间T增加一个介于±(0.001~0.005) s之间的随机时间,得到新的变目标控制策略调节时间T,重复步骤(2)(3)直至找到最优值。 如图8所示,在PSCAD/EMTDC仿真平台上搭建三端柔性直流输电模型,仿真验证设计的变目标控制策略对多端柔性直流输电系统的影响。 图8 三端柔性直流输电系统拓扑结构Fig.8 Three-terminal MMC-HVDC topology 各换流站参数设定值如表1所示。 表 1 各换流站参数Tab.1 Parameters of converter stations 三端柔性直流输电系统采用主从控制,换流站1为主控制站,采用定直流电压控制和定无功功率控制;换流站2、3为从控制站,采用定直流侧有功功率控制和定无功功率控制。换流站2作为备用主控站,当换流站1故障停运时,上层控制系统自动把主控站释放给换流站2,换流站2控制方式变为定直流电压控制和定无功功率控制。 在换流站1模拟交流侧三相短路故障,故障点设置在变压器和MMC换流站之间,故障使换流站变压器和MMC换流站每一相都产生过电流,如果不及时切除故障,可能导致元件损坏甚至系统崩溃。设置系统在5.05 s时发生交流侧三相短路故障,持续0.1 s,故障后0.05 s,交流断路器启动,切除短路故障,换流站1紧急停运,上层控制器使换流站2切换到定直流电压控制。在换流站2的定直流电压控制加入变目标控制环节,加入变目标控制环节的外环PI参数整定为Kp1=2000,KI1=0.01;内环控制PI参数整定为Kp2=1,KI2=0.01;经优化后变目标控制策略的调节时间T=0.103 s。作为对比的经典外环控制PI参数整定为Kp1=20,KI1=0.01,内环控制PI参数整定为Kp2=1,KI2=0.01。图9中VAPI曲线是采用变目标控制策略的控制曲线,PI曲线是采用经典双环控制策略曲线。 图9 系统三相短路故障响应Fig.9 Response to three-phase short circuit of transmitting terminal 短路故障切除后,为了稳定直流电压,换流站2需要补偿换流站1闭锁导致的不平衡功率,经典双环控制和加入变目标控制环节后的双环控制都能使系统经过一定时间后达到稳定的直流电压和有功功率。但从图9的仿真结果可以看出,加入变目标控制环节后的控制系统比经典双环控制系统调节速度更快,超调量更小。采用变目标控制策略后,换流站2有功功率上升时间比采用经典双环控制策略缩短33.3%,换流站3有功功率上升时间也缩短33.7%。对于关系到直流输电系统稳定的直流电压,两种控制方式的直流电压上升时间相同,但是经典双环控制策略下电压超调量为46.7%,而变目标控制策略下的电压超调量几乎为0。 可见,在暂态故障后的恢复过程中,采用加入变目标控制策略的双环控制能有效加快恢复速度,减少超调量。 5.2.1 相同目标不同PI参数控制效果 在三端柔性直流输电系统模拟换流站2有功功率阶跃指令提升1 p.u.,实现潮流反转,观察换流站2有功功率变化情况。在5.1 s时,换流站2收到有功功率阶跃指令,提升1 p.u.。换流站2采用定有功功率控制策略,并采用变目标控制策略,设置不同的内外环控制系统PI环节参数,如表2所示。考察相同目标不同控制参数下的控制效果,验证控制系统的鲁棒性。 表2 仿真曲线与控制参数对应表Tab.2 Control parameters 由图10可知变目标控制策略在不同双环控制PI参数下,都能较好地按照所设定的变目标控制曲线达到目标值,变目标控制策略可以有效降低系统对控制参数的敏感性。 图10 相同目标不同PI参数换流站2直流侧有功功率控制效果Fig.10 Control effect of converter station 2 active power with different PI parameters on the same target 5.2.2 不同目标下控制系统的适应性 为了检验采用变目标控制策略的MMC-HVDC控制系统在相同控制参数下对不同目标值的阶跃响应能否根据设计的目标曲线分步达到目标值,对换流站2进行不同目标值下的有功功率阶跃试验,考察换流站2有功功率的阶跃响应。5.1 s时,换流站2收到有功功率阶跃指令,提升1 p.u.,1.5 p.u.,-0.5 p.u.。换流站2采用定有功功率控制策略,并加入变目标控制环节,其中外环控制PI参数整定为Kp1=400,KI1=0.01,内环控制PI参数整定为Kp2=1,KI2=0.01,变目标控制策略的调节时间T=0.103 s。 由图11可知,系统对不同目标值的阶跃响应都能很好地跟踪变目标控制曲线,并快速且无超调地达到最终的目标值。这说明加入变目标控制环节可以有效降低MMC-HVDC控制系统对控制对象和控制目标的敏感性,提高控制系统的适应性。 图11 不同目标相同控制参数的换流站2有功功率阶跃响应Fig.11 Step response of converter station 2 active power with the same control parameters on different targets 本文根据简化后的MMC-HVDC数学模型和离散的内外环控制设计了变目标控制策略,推导了加入变目标控制环节后的控制系统PI参数设置原则,并对变目标控制策略调节时间进行优化。最后在PSCAD/EMTDC仿真平台上对所设计的MMC-HVDC变目标控制策略进行仿真验证,仿真结果显示所设计的变目标控制策略可以使MMC-HVDC控制系统PI参数整定范围增大,增强控制系统的鲁棒性,并且解决了直流有功功率和直流电压调整中快速性和超调量之间的矛盾,具有良好的稳态和暂态运行性能。 参考文献: [1] MUYEEN S M, TAKAHASHI R, TAMURA J.Operation and control of HVDC-connected offshore wind farm[J]. IEEE Trans on Sustainable Energy, 2010, 1(1): 30-37. [2] 徐 政, 张哲任, 刘高任. 柔性直流输电网的电压控制原理研究[J]. 电力工程技术, 2017, 36(1): 54-59. XU Zheng, ZHANG Zheren, LIU Gaoren. Research on voltage control principle of flexible DC transmission power grid[J]. Electric Power Engineering Technology, 2017, 36(1): 54-59. [3] 刘志江,夏成军,杜兆斌. 多端柔性直流输电系统直流电压模糊控制策略[J]. 电力工程技术, 2017, 36(2): 21-26,87. LIU Zhijiang, XIA Chengjun, DU Zhaobin. Research of DC voltage fuzzy control strategy for VSC-MTDC systems[J]. Electric Power Engineering Technology, 2017, 36(2): 21-26,87. [4] 张 昕,杜俊杰,曾 东,等. 含VSC-HVDC系统的风光并网极限容量的研究[J]. 浙江电力,2016,35(12):64-68. ZHANG Xin,DU Junjie,ZENG Dong,et al.Capacity limit research on grid integration of wind and PV power with VSC-HVDC systems[J].Zhejiang Electric Power,2016,35(12):64-68. [5] 管敏渊, 徐 政. 模块化多电平换流器型直流输电的建模与控制[J]. 电力系统自动化, 2010, 34(19): 64-68. GUANG Minyuan, XU Zheng. Modeling and control of modular multilevel converter in HVDC transmission[J]. Automation of Electric Power Systems, 2010, 34(19): 64-68. [6] 范心明, 管 霖, 夏成军,等. 基于PCHD模型的柔性直流输电鲁棒控制[J]. 电力系统自动化, 2013, 37(15): 40-46. FAN Xinming, GUAN Lin, XIA Chengjun, et al. PCHD based robust control of VSC-HVDC transmission based on Port-controlled Hamiltonian with Dissipation[J]. Automation Of Electric Power Systems, 2013, 37(15):40-46. [7] RUAN S Y, LI G J, JIAO X H, et al. Adaptive control design for VSC-HVDC systems based on backstepping method[J]. Electric Power Systems Research, 2007, 77(5-6): 559-565. [8] 赵成勇, 李金丰, 李广凯. 基于有功和无功独立调节的VSC-HVDC控制策略[J]. 电力系统自动化, 2005, 29(9): 24-28,34. ZHAO Chengyong, LI Jinfeng, LI Guangkai. VSC-HVDC control strategy based on respective adjustment of active and reactive power[J]. Automation of Electric Power Systems, 2005, 29(9): 24-28,34. [9] 董云龙, 包海龙, 田 杰, 等. 柔性直流输电控制及保护系统[J]. 电力系统自动化, 2011, 35(19): 89-92. DONG Yunlong, BAO Hailong, TIAN Jie, et al. Control and protection system for VSC-HVDC[J]. Automation Of Electric Power Systems. 2011,34(19):89-92. [10] COLE S, BELMANS R. A proposal for standard VSC HVDC dynamic models in power system stability studies[J]. Electric Power Systems Research, 2011, 81(4):967-973. [11] 郑连清, 池俊锋, 陆治国. 基于三级模糊自适应PI控制的VSC-HVDC控制器设计[J]. 电力系统保护与控制, 2011, 39(23):117-122. ZHENG Lianqing, CHI Junfeng, LU Zhiguo. Three-step fuzzy adaptive PI controller for VSC-HVDC system[J]. Power System Protection and Control, 2011, 39(23): 117-122. [12] 郑连清, 池俊锋. 新型VSC-HVDC控制器设计[J]. 电网技术, 2012, 36(3): 210-216. ZHENG Lianqiang, CHI Junfeng. Design of a new type of VSC-HVDC controller[J]. Power System Technology, 2012, 36(3): 210-216. [13] 何大清, 蔡 旭. 基于平坦系统的VSC-HVDC控制[J]. 电工技术学报, 2012(12): 233-239. HE Daqing, CAI Xu. Flatness-based control of VSC-HVDC[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 233-239. [14] 魏晓光, 汤广福, 郑健超. 电压源高压直流输电离散模型及其控制策略[J]. 中国电机工程学报, 2007, 27(28): 6-11. WEI Xiaoguang, TANG Guangfu, ZHENG Jianchao. Study of VSC-HVDC discrete model and its control strategies[J]. Proceedings Of The Chinese Society For Electrical Engineering, 2007, 27(28): 6-11. [15] 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 北京:国防工业出版社, 2008. HAN Jingqing. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M].Beijing: National Defence Industry Press, 2008. [16] 黄焕袍, 万 晖, 韩京清. 安排过渡过程是提高闭环系统“鲁棒性、适应性和稳定性”的一种有效方法[J]. 控制理论与应用, 2001, 18(s1): 89-94. HUANG Huanpao, WAN Hui, HAN Jingqing. Arranging the transient process is an effective method improved the "robustness, adaptability and stability” of closed-loop system[J], Control Theory & Application, 2001, 18(s1): 89-94. [17] 郭 捷. 模块化多电平换流器在HVDC应用的若干关键问题研究[D]. 杭州:浙江大学, 2013. GUO Jie. Research on several issues in modular multilevel converter for HVDC application[D]. Hangzhou: Zhejiang University, 2013. [18] 郭 赣, 朱 熙. 基于过渡过程安排的PID控制器设计[J]. 宇航学报, 2012, 33(7): 930-935. GUO Gan, ZHU Xi. Design of PID controllers based on arranging the transient process[J]. Journal of Astronautics, 2012, 33(7): 930-935. [19] 杨启文, 阳外玲, 薛云灿,等. 基于Maclaurin展开的时间绝对误差积分次优时滞系统设计[J]. 控制理论与应用, 2011, 28(12):1831-1836. YANG Qiwen, YANG Wailing, XUE Yuncan, et al. Design of integral time absolute error suboptimal tiem-delay system based on Maclaurin expansion[J]. Control Theoty & Applications, 2011, 28(12): 1831-1836.
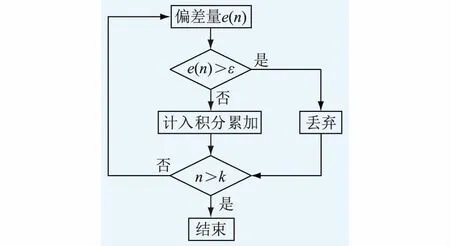
4 变目标控制策略调节时间T的设置
4.1 改进的ITAE性能指标

4.2 变目标控制策略最优调节时间
5 仿真验证

5.1 暂态故障恢复过程中变目标控制策略的控制效果
5.2 变目标控制系统的鲁棒性和适应性
6 结语

