肝肿瘤射频消融温度场仿真技术研究综述

王笑茹，高宏建，吴水才，白燕萍

北京工业大学 生命科学与生物工程学院，北京 100124

引言

肝肿瘤是威胁人类生命健康的重大疾病之一，具有恶性程度高且生长迅速等特点，是世界第三大癌症死亡原因[1]。我国是肝癌高发地区，发病人数占全球的45%[2]，因此肝肿瘤的有效治疗已成为亟待解决的社会问题。目前治疗肝肿瘤的首选方法仍是外科手术，由于各种禁忌症（例如患者体内肿瘤太多或肿瘤位于不可切除位置等原因）每年仅有20%左右的肝肿瘤患者适宜进行外科切除手术[3-4]。针对不能进行外科切除的肝肿瘤患者，热消融技术治疗肝肿瘤已成为行之有效的方法。与外科切除手术相比，热消融治疗具有低发病率、低死亡率、低成本以及适用于实时成像指导等特点。目前消融技术主要包括激光消融、冷冻治疗、微波消融、射频消融（Radiofrequency Ablation，RFA）、高功率超声聚焦消融和无水乙醇注射治疗[5-6]。RFA技术用于治疗肝肿瘤疾病具有微创、有效和安全性等特点，已成为全世界应用最广泛的消融技术。

随着计算机仿真技术的不断发展，越来越多的学者采用有限元仿真技术建立肿瘤消融区域的温度场分布模型，由此不仅能够实时地预测消融区温度变化，而且能够辅助医生术前制定合理的手术计划[7]。本文主要针对肝肿瘤射频消融原理、温度场仿真和RFA中的影响因素等内容进行综述，最后指出了目前仿真建模中存在的不足。

1 肝肿瘤射频消融原理

RFA治疗患者体内的肿瘤是通过使用超声、计算机断层扫描（Computed Tomography，CT）或磁共振（Magnetic Resonance Imaging，MRI）引导，将一个或多个射频消融电极针插入患者肿瘤组织中[8]，利用交变电流（350～500 kHz）[9]产生的热量实现对肝癌细胞的原位灭活。RFA的加热目标是60℃～100℃，该温度可导致肿瘤组织发生不可逆的损伤，当温度超过100℃～110℃时会导致组织发生炭化和汽化现象[10]。RFA对于治疗小于3 cm的肝肿瘤具有良好的效果[11]。肝肿瘤射频消融原理和组织加热原理图，见图1[12]。该装置主要包括射频发生器、射频消融电极和负电极板，射频消融电极作为正电极用来插入靶组织进行热消融，皮肤电极作为负电极板放置于患者的大腿处或背部。射频发生器产生的交流电从射频消融电极流到负电极板。射频消融电极、射频发生器、负电极板和患者构成了一个闭环回路。整个消融过程中，由于自由离子（主要是Na+，K+和Cl-）随着RF电流方向进行变化，射频消融电极周围靶组织内会产生离子间的相互作用，导致局部温度升高，使肿瘤组织发生凝固性坏死。

图1 肝肿瘤射频消融原理和组织加热原理图

2 RFA温度场仿真的关键技术

射频消融温度场仿真建模中的关键技术主要包括能量沉积计算、生物传热方程的求解、组织特性参数分析和靶组织热损伤评价等内容。其中，生物组织特性参数（电特性参数和热物性参数）对热消融损伤区的几何形状、体积大小具有显著影响。

2.1 RFA仿真中的能量沉积

RFA期间靶组织中的能量（W/kg）由比吸收率（S pecific Absorption Rate，SAR）确定，SAR的具体表达式如下：

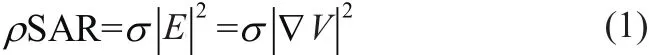
其中E (V/m)表示电场强度；ρ (kg/m3)表示密度；V (V)表示电势；σ (S/m)表示电导率。由于RFA期间σ是依赖于组织损伤程度和水含量变化的，SAR每次都需要重新计算。

RFA期间，可通过求解拉普拉斯方程得到SAR的电场分布，表达式如下：

其中Δ表示梯度算子，；V表示每一点的电势，单位（V）；σ (S/m)表示依赖于温度变化的电导率。RFA电极针的工作频率范围为350～550 kHz，在RFA仿真建模中常常将此频率范围内的交流电简化为直流电[13-14]。

2.2 生物传热方程研究现状

温度场仿真建模时通常利用生物传热方程计算生物组织内热量的传递，目前主要存在以下4种类型的生物传热方程：基于傅里叶传热规律的Pennes方程、基于非傅里叶传热规律的Hyperbolic方程、多孔介质传热模型和Weinbaum-Jiji方程。

2.2.1 Pennes方程

Pennes在1948年提出了Pennes生物传热方程[15]，该表达式简单，至今仍是应用最广泛、最经典的生物传热模型。该方程考虑了血流和生物代谢活动的影响，引入了血液灌注项，具体表示如下：

其中T表示组织温度（℃）；Tb表示动脉血液温度（℃）；t表示时间(s)；ρ表示体积质量密度（kg/m3）；c表示比热容[J/(kg·K)]；k表示导热率[W/(m·K)]；ωb表示血液灌注率（s-1）；Qm表示代谢热生成速率，单位（W/m3）；Qhs表示由RFA发生器产生的热量，单位（W/m3）；下标b表示组织的血液特性；ε0表示真空中的介电常数，ε0=8.8541×10-12F/m ；肝脏组织中 εr=2770。

经典的Pennes生物热方程已广泛应用于肿瘤热消融、热疗和冷冻烧伤等领域，但该方程过于简化，忽略了血流速度和血管形状，其假设组织内血液的对流换热发生在毛细血管的肌肉层中。近年来一些学者基于经典的Pennes方程对血管和组织间的传热规律进行了研究，张燕等[16]改进了Pennes方程中的血液灌注项，此血液灌注项表示血管和组织间的局部换热量，与传统的Pennes方程相比该方程能够描述血管树对组织温度分布的影响。陈琦等[17]基于经典的Pennes方程提出了混合生物传热模型，包括组织、静脉和动脉3个传热方程。此外，马吉明等[18]又在混合生物传热模型[19]的基础上根据血管树形态模型和单根血管轴向温度变化规律，对上述方程进行了改进。

2.2.2 Hyperbolic方程

基于傅里叶传热规律的Pennes生物热方程通常不能描述超常规热传递情况，众多学者开始考虑采用基于非傅里叶热传递规律的模型进行组织温度场的预测。在非傅里叶传热模型中，应用最普遍的是双曲线（Hyperbolic）传热模型，具体表示如下：

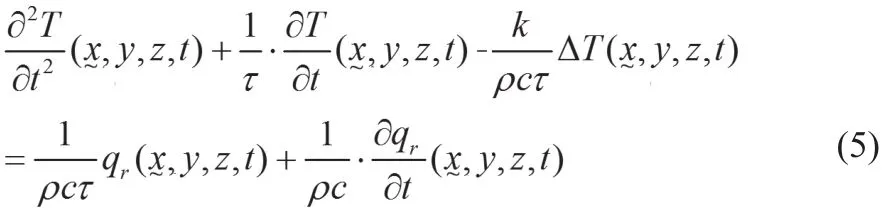
其 中表 示 特 定 点 在t时 刻 的 温 度(s)。τ表示弛豫时间，被定义为热能量传递到生物组织内的最近单元所需的特征时间，对于肝组织而言，τ=16 s[20]。

Hyperbolic方程因其考虑到组织热扩散存在弛豫时间而具有更高的准确性，也越来越受到人们的关注，一些学者对Hyperbolic生物传热模型在肝肿瘤热消融中的应用进行了研究。López-Molina等[21]评估了用于肝肿瘤射频消融的Hyperbolic传热方程，与Pennes方程相比 该传热方程具有以下特点：在初始阶段温度上升快；具有较高的仿真温度值；由于该方程考虑了弛豫时间τ，温度变化有所延迟。Zhang等[22]分别构建了基于Pennes方程和Hyperbolic方程的温度场仿真模型，发现相同设置条件下基于非傅里叶传热规律的Hyperbolic方程可用于长时间和高功率的RFA仿真中。

2.2.3 多孔介质传热模型

Chen和Holmes首先提出了生物组织中进行热传递的多孔介质模型，该模型将组织分成固体和液体两部分进行建模，生物组织中的热量传递具体表示如下：

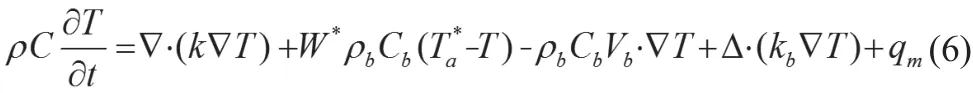
其中kb表示小血管中血液灌流所引起的组织导热系数的表观增加，Vb表示组织中总的血液灌注矢量，其余参数如上所述。

由于Chen和Holmes模型需要知道血管的几何数据，使得该模型难以应用到实际中。王补宣等[23]充分考虑了组织骨骼导热、血液对流、血液导热和内源热，将生物组织看成是由细胞组成的多孔体骨架，血管、淋巴管等构成组织液的通道，构建了一个多孔介质的生物传热模型。该传热模型适用于预测不含大动脉和大静脉的肌肉组织的温度分布情况。

2.2.4 Weinbaum-Jiji方程

Weinbaum和Jiji提出了Weinbaum-Jiji方程（W-J方程），W-J方程是建立在每条血管的血流换热的基础上的血管传热模型，能够获得血流和血管周围组织的温度分布情况，W-J方程可以表示为[24]：

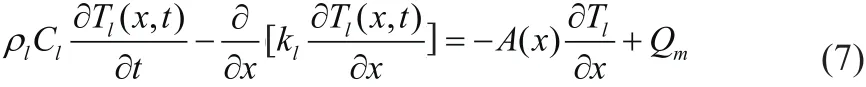
其中，，kt表示组织热导率；，keff表示有效热导率，a表示血管半径，n表示血管数密度，l1表示血管长度，σ表示随皮肤深度变化的系数。

目前学者普遍倾向于W-J模型结构，即通过分层的方法来描述不同组织内的传热规律，通常W-J方程用于需要考虑血管空间分布时的热传递求解。但W-J方程在仿真建模中应用时难以推广，主要包括两方面原因：一是实际应用中需要提前获得组织血管的大小、密度、流向和速度等数据；二是该模型的求解过程很复杂。

2.3 靶组织热损伤评价

靶组织损伤（Target Tissue Necrosis，TTN）的评估是RFA临床应用治疗计划的重要组成部分，通常采用等温线阈值、热等效剂量（Thermal Isoeffective Dose，TID）和Arrhenius模型等方法对RFA仿真模型中的组织损伤情况进行评估[12]。在利用等温线阈值法对组织进行损伤评估时，通常以50℃～60℃范围内的温度阈值作为治疗指标[25]，即当组织温度超过该阈值时则认为组织已损伤，其中常用的温度阈值包括50℃[26-27]、55℃[28]和60℃[29]。此外，RFA过程中生物组织发生不可逆性坏死不仅取决于靶组织温度，同时还和靶组织类型和热消融时间有关。目前TID和Arrhenius模型被广泛地应用于RFA仿真建模中以进行靶组织热损伤评价。采用累积等效时间对TID模型进行定量评价的方法通常选取43℃作为参考温度值，根据生物效应的原理将不同的温度/时间换算为43℃/min（即CEM43）[7]，具体表达式如下：

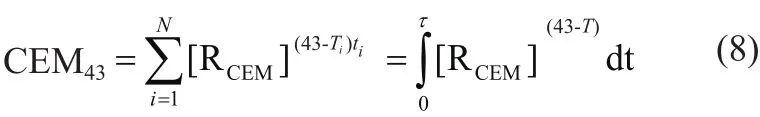
RCEM是无量纲因子，其表示当温度升高1℃时，细胞产生相同存活率所需的暴露时间的比例。当T≥43℃时，RCEM=0.5； T＜43℃时， RCEM=0.25。T 表示温度，单位（℃）。但TID模型只能预测由较低温度引起的生物组织损伤（例如43℃～50℃），当温度高于50℃并不适用[30]。

Arrhenius模型由Henriques和Moritz在1947年提出，该模型考虑了组织温度和热消融时间的累积效应，描述了生物组织温度、损伤程度和暴露时间的指数关系，具体表达式如下：

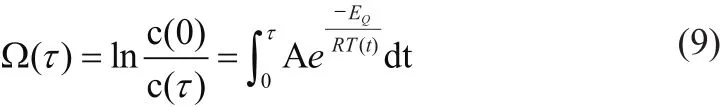
Ω(τ)表示组织坏死程度；c(0)表示未受暴露时生物组织细胞内未受损细胞的比例；c(τ)表示τ时刻组织内未受损细胞的比例；A表示频率因子，单位(s-1)；Eq表示生物反应能量，单位（J/mol）；R表示通量气体常数，R=8.314 J/mol·K；T(t)表示绝对温度。肝肿瘤组织中有：A=3.247×1043s-1，E=2.814×105J/mol[27]。但该模型仅考虑了细胞坏死过程中单一的不可逆转的变化，而实际细胞死亡过程是由多个可逆和相互作用的过程组成的。例如，轻度受损的 细 胞可以在一段时间后恢复并最终进入“活跃”状态，而死亡细胞无法恢复。

考虑到RFA过程中组织发生不可逆性坏死是由多个可逆和相互作用的过程构成的，O’Neill等[31]用活跃（A）、受损（V）和死亡（D）这3种状态对细胞坏死过程进行描述，其中kf和kb表示细胞不同状态间的变化率。Qadri等[32]采用O’Neill细胞坏死模型对RFA过程中的受损组织进行评估，初始阶段取A=0.99，D=0.01。

3 RFA仿真中的影响因素

RFA过程中当消融时间和功率固定时，其消融区域的形状和体积主要受到生物组织特性参数（热物性参数和电参数）、大血管的冷却作用和射频消融电极等多种因素的影响。

3.1 生物组织特性参数

RFA过程中生物组织特性参数（如电阻抗、电导率、介电常数、导热率、比热容、组织密度和血液灌注率等参数）是随温度动态变化的，其对RFA消融效果具有重要影响。即使在同一组织器官内不同位置的组织特性参数也存在较大差异[33]。组织加热是一个极其复杂的过程，当生物组织大于40℃时组织细胞分子结构将发生变化，此过程将会导致组织的热物性和电特性参数发生可逆和不可逆的变化[34]。

3.1.1 热物性参数

生物组织热物性参数主要包括导热率k[W/(m·K)]、比热容c[J/(kg·K)]、组织密度ρ(kg/m3)和血液灌注率ωb等参数，在RFA期间组织热物性参数是随温度而变化的。Zhang等[35]考虑了肝肿瘤和正常肝组织导热率的温度依赖性，对导热率参数进行了分段表达：

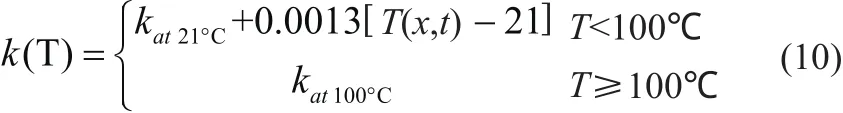
Cavagnaro等[36]采用分段式多项式函数对肝脏组织的导热率和比热容进行了拟合：

研究表明当生物组织温度在20℃～100℃范围内时，组织的热物性参数可以根据组织中含水量和水的热物性质来表示，具体表示如下：

其中w表示组织中水含量的百分比，肝组织中约为69%。T(℃)表示组织温度。kρ、kc和kk分别表示依赖于温度的水的密度、水的比热容和水的导热率，表达式如下：

对于高灌注组织（例如肝脏组织和肾），血液灌注充当散热器。血液灌注率的物理意义是单位时间内单位体积组织中的血液流量，血液灌注对RFA模型具有很大的影响，消融过程中血液灌注率随温度的变化是十分复杂的。Liu等[37]提出了随温度变化的血液灌注率函数，表达式如下：

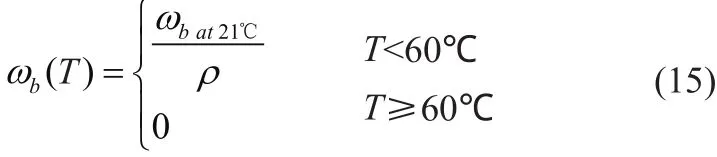
此外，研究发现血液灌注的变化高度依赖于组织/肿瘤损伤的程度[38]，表达式如下：

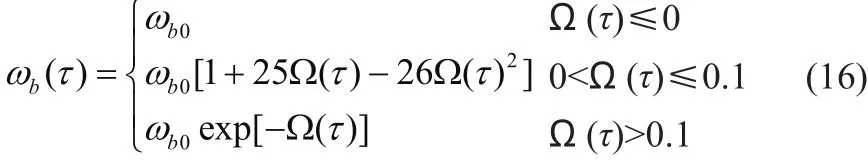
其中ωb0表示组织内组织/肿瘤的血液灌注率；Ω(τ)表示组织损伤程度。

3.1.2 电特性参数

肝肿瘤射频温度场仿真模型中的生物组织电特性参数包括电导率σ和介电常数ε，这些参数将直接影响电磁能量的沉积。在先前的仿真建模研究中，人们常常忽略电特性参数对温度的依赖性，选用固定的电导率和介电常数，使得仿真结果与实际消融效果存在较大偏差。

当组织温度小于100℃时，Trujillo等[39]提出了线性变化的电导率和介电常数的表达函数：

其中σ0和ε0分别表示电导率和介电常数，Δσ和Δε分别表示电导率和介电常数变化率，T0表示初始温度。许多学者对电导率参数进行研究发现，当生物组织温度大于100℃时电导率的变化趋势会发生变化，这一现象是由于温度大于100℃时组织中的水发生汽化引起的，因此对电导率参数进行分 段表达，表达式如下：

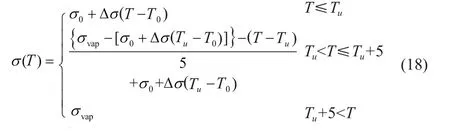
其中T∈[Tl,Tu]，Tl和Tu分别表示温度的最低和最高值；σ0表示基准电导率；Δσ表示开尔文温度变化1℃时电导率的变化值；T0表示参考温度，其大小是测量σ0和σvap时的温度值。

3.2 大血管冷却作用

肿瘤是一种生长在血管附近的组织，由于血液对流必定会带走一部分热量，所以血管附近消融区温度偏低，导致靶组织不能被完全破坏，从而导致术后复发等现象。大血管（即指直径大于3 mm的血管）对射频消融温度场具有显著的冷却作用[40]，建模仿真中主要研究血管的形状、血管直径、血流速度以及血管与肿瘤之间的距离对温度场分布的影响。血管直径和平均血流速度间的关系[41-42]，见表1。

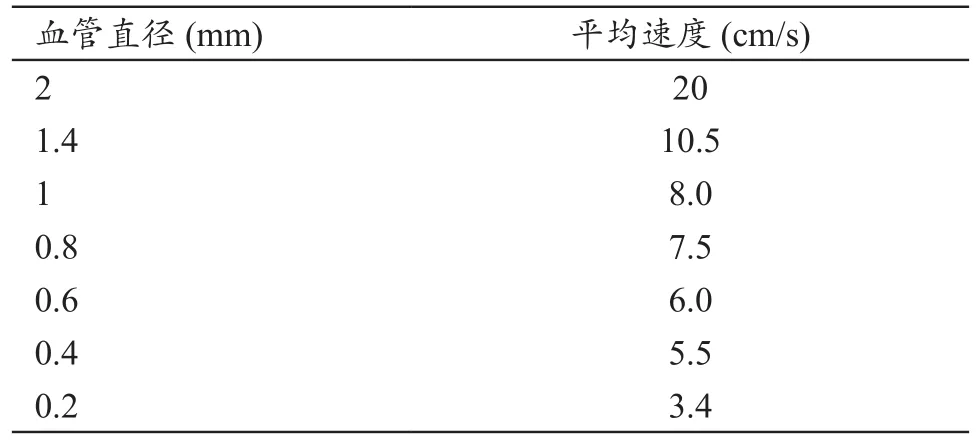
表1 血管直径和平均血流速度

Huang等[28]针对含有血管的肝肿瘤射频仿真模型进行研究，当射频电极针与血管平行放置时比垂直放置时血管产生的冷却作用更加显著。另外，减少血流速度可以降低大血管的冷却作用。Shao等[43]在射频仿真模型中加入了分形树状形状的血管模型，并进一步研究了血管的直径、血管距离消融针的距离和分形树状形状的血管个数对温度场分布的影响。研究表明在加热过程中血管距离消融针的距离对消融结果的影响最为显著。Al-Alem等[44]分析了血管对单针伞状电极和平行双螺旋电极消融区域的影响，发现平行双螺旋电极消融区受血管冷却作用的影响较小。

3.3 射频消融电极针

RFA消融过程中消融电极针类型、插针位置等因素对消融区的几何形状、大小和体积的影响十分显著。RFA消融电极针通常可根据电极针构造、是否外接负电极板和电极手柄数目进行分类（图2）[45-46]。

图2 RFA电极针分类

在临床中，凝固区尺寸成为RFA治疗大肿瘤的主要限制因素，大于3 cm的肿瘤具有较高的术后局部复发率[47]。针对中等大小的肿瘤（≥4 cm）往往需要采用重叠消融进行治疗[48]。射频温度场仿真模型中通常使用比较复杂的电极针系统，例如复合电极针、双电极针和集束电极等进行RFA治疗。研究发现采用射频单电极针和多电极针交替系统对患者进行RFA手术，3年内患者肿瘤复发的概率仅为11%[49]。在RFA仿真建模中电极针的类型、组合形式、电极激活模式和其插入组织中的位置等内容一直以来都是研究的重点。Huang[50]研究了水冷式多电极针之间的距离对消融区的影响，发现使用两个电极针进行RFA时，电极间距小于2 cm的重叠消融效果显著，随着间 距不断变大（＞2 cm），非连续凝固区逐渐增加。Lee等[51]设计了一种 “爪状”RFA电极针，并通过仿真和实验与集束电极结果进行对比，表明开关式“爪状”电极针能有效地扩大消融区体积。另外发现，单个射频电极针与多个电极针的交替使用能够有效、安全地获得更大的消融体积[52]。Soetaert等[53]发现脉冲模式下工作的双极射频消融针能有效地增加消融区域。为了解决多点RFA过程中出现的“漏空效应”（即各消融位点间未被消融的区域），Mulier等[54]采用矩阵式RFA模式（Matrix Radiofrequency Ablation，MRFA），通过离体猪肝实验建立了2×2的矩阵消融电极系统、且相邻电极间距为3 cm，但该电极系统在仿真中存在中心温度过高的情况。Shao等[55]改进了此电极系统：4个负消融电极分别放置于正方形顶角，正消融电极位于正方形中心处。结果表明，该电极系统能够在增大消融区域的同时有效地降低组织中心温度，因而更适合于矩阵式RFA。

4 总结

虽然众多学者已经建立了多种类型的肝肿瘤射频消融仿真模型，同时也取得了一定的成果，但射频温度场仿真中仍存在以下问题：① 模型的建立大多都是基于离体猪肝实验或体模实验的结果，忽略了人体组织间的差异性；② 忽略了对肝脏组织内部结构如血管、肿瘤等进行建模与仿真分析；③ 虽然已有学者研究了生物组织特性参数随温度变化的关系，但目前大多数射频仿真模型中生物组织参数仍选用固定值；④ 将射频发生器产生的交流电简化为直流电。

由于RFA仿真建模消融区域易受生物组织特性参数、大血管冷却作用和射频消融电极等因素的影响，使得仿真建模结果和实际情况存在较大误差。目前针对大型肿瘤（＞3 cm）：射频仿真建模中使用复合电极针和矩阵电极系统产生重叠消融区进行热消融；采用脉冲模式工作（正弦波或方波）的电极针系统；单个射频电极针与多个电极针交替使用进行RFA。此外，研究表明注入NACl溶液能够有效扩大消融区体积[33,56]；为了减小仿真误差，仿真模型中的敏感性参数（即对消融结果影响显著的参数）可采用依赖温度变化的函数，如射频消融中对电导率参数和导热率参数使用随温度线性变化的模型。

[1] Pascual S,Herrera I,Irurzun J.New advances in hepatocellular carcinoma[J].World J Hepatol,2016,8(9):421-438.

[2] 常玉梅.人体微波肿瘤治疗中的热场分析及应用[D].南京:南京理工大学,2009.

[3] Nordlinger B,Benoist S.Treatment options for metastatic liver cancer.Surgical resection including perioperative chemotherapy(adjuvant and neoadjuvant)[J].Eur J Cancer,2003,1:181-188.

[4] Lovet JM,Bruix J.Novel advancements in the management of hepatocellular carcinoma in 2008[J].J Hepatol,2008,48:S20-S37.

[5] Kang TW,Rhim H.Recent advances in tumor ablation for hepatocellular carcinoma[J].Liver Cancer,2015,4(3):176-187.

[6] 李志艳.经皮热消融治疗疑难部位肝肿瘤引导技术的临床应用进展[J].传染病信息,2016,29(6):378-381.

[7] 罗洪艳,黄维,潘进洪,等.射频消融建模仿真的研究进展[J].激光杂志,2014,35(1):1-4.

[8] Chu KF,Dupuy DE.Thermal ablation of tumours:biological mechanisms and advances in therapy[J].Nat Rev Cancer,2014,14(3):199.

[9] Xiao,Chen,Hai-Peng,et al.Advances in non-surgical management of primary liver cancer[J].World J Gastroentero,2014,20(44):16630-16638.

[10] Lencioni R,Crocetti L.Radiofrequency ablation of liver cancer[J].Vasc Interv Radiol,2007,10(1):38-46.

[11] Meyer J,Toomay S.Update on treatment of liver metastases:focus on ablation therapies[J].Curr Oncol Rep,2015,17(1):420.

[12] Zhang B,Moser MAJ,Zhang EM,et al.A review of radiofrequency ablation:Large target tissue necrosis and mathematical modelling[J].Phys Medica,2016,32(8):961-971.

[13] Tungjitkusolmun S,Staelin ST,Haemmerich D,et al.Threedimensional finite-element analys es for radio-frequency hepatic tumor ablation[J].IEEE T Bio-Med Eng,2002,49(1):3-9.

[14] Barauskas R,Gulbinas A,Vanagas T,et al.Finite element modeling of cooled-tip probe radiofrequency ablation processes in liver tissue[J].Comput Biol Med,2008,38(6):694-708.

[15] Pennes HH.Analysis of tissue and arterial blood temperatures in the resting human forearm[J].J Appl Physiol,1948,1(2):93-122.

[16] 张燕,乐恺,张欣欣.基于模拟血管树以及改进 Pennes 方程的生物传热模型[J].热科学与技术,2006,5(4):306-312.

[17] 陈琦,白景峰,陈亚珠.伴行血管在高强度聚焦超声下对温度场的影响[J].上海交通大学学报,20 04,38(1):130-134.

[18] 马吉明,张向梅,苏日建,等.基于混合生物热传导模型的Pennes方程的改进[J].郑州轻工业学院学报 (自然科学版),2015 (2):16-21.

[19] 陈琦,白景峰,陈亚珠.伴行血管在高强度聚焦超声下对温度场的影响[J].上海交通大学学报,2004,38(1):130-134.

[20] Molina JAL,Rivera MJ,Trujillo M,et al.Thermal modeling for pulsed radiofrequency ablation: analytical study based on hyperbolic heat conduction.[J].Med Phys,2009,36(4):1112-1119.

[21] López-Molina JA,Rivera MJ,Trujillo M,et al.Assessment of hyperbolic heat transfer equation in theoretical modeling for radiofrequency heating techniques[J].Bio Eng,2008,2:22.

[22] Zhang M,Zhou Z,Wu S,et al.Simulation of temperature field for temperature-controlled radio frequency ablation using a hyperbolic bioheat equation and temperature-varied voltage calibration: a liver-mimicking phantom study[J].Phys Med Biol,2015,60(24):9455-9471.

[23] 王补宣,王艳民.生物传热基本方程的研究[J].工程热物理学报,1993,14(2):166-170.

[24] Song WJ,Weinbaum S,Jiji LM.A theoretical model for peripheral tissue heat transfer using the bioheat equation of Weinbaum and Jiji[J].J Biomech Eng,1987,109(1):72-78.

[25] Prakash P,Diederich CJ.Considerations for theoretical modelling of thermal ablation with catheter-based ultrasonic sources:Implications for treatment planning,monitoring and control[J].Int J Hyperther,2012,28(1):69-86.

[26] Pérez JJ,Muñoz V,Berjano E.Computer modeling of electrical and thermal performance during bipolar pulsed radiofrequency for pain relief[J].Med Phys,2014,41(7):071708.

[27] Arenas J,Perez JJ,Trujillo M,et al.Computer modeling and ex vivo experiments with a (saline-linked) irrigated electrode for RF-assisted heating[J].Biomed Eng Online,2014,13(1):164-173.

[28] Huang HW.Influence of blood vessel on the thermal lesion formation during radiofrequency ablation for liver tumors[J].Med Phys,2013,40(7):073303.

[29] Haase S,Süss P,Schwientek J,et al.Radiofrequency ablation planning:An application of semi-infinite modelling techniques[J].Eur J Oper Res,2012,218(3):856-864.

[30] Reddy G,Dreher MR,Rossmann C,et al.Cytotoxicity of hepatocellular carcinoma cells to hyperthermic and ablative temperature exposures:in vitro studies and mathematical modelling[J].Int J Hyperther,2013,29(4):318-323.

[31] O’Neill DP,Peng T,Stiegler P,et al.A three-state mathematical model of hyperthermic cell death[J].Ann Biomed Eng,2011,39(1):570-579.

[32] Qadri AM,Chia NJY,Ooi EH.Effects of saline volume on lesion formation during saline-infused radiofrequency ablation[J].Appl Math Model,2017,43:360-371.

[33] Ahmed M,Solbiati L,Brace CL,et al.Image-guided tumor ablation:standardization of terminology and reporting criteria—a 10-year update[J].J Vasc Interv Radiol,2014,25(11):1691-1705.

[34] Rossmann C,Haemmerich D.Review of temperature dependence of thermal properties,dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures[J].Crit Rev Biomed Eng,2014,42(6):467-492.

[35] Zhang B,Moser MA,Zhang EM,et al.Numerical analysis of the relationship between the area of target tissue necrosis and the size of target tissue in liver tumours with pulsed radiofrequency ablation[J].Int J Hyperther,2015,31(7):715-725.

[36] Cavagnaro M,Pinto R,Lopresto V.Numerical models of microwave thermal ablation procedures[A].Microwave Conference (EuMC), 2014 44thEuropean[C].New York:IEEE,2014:480-483.

[37] Liu Z,Ahmed M,Sabir A,et al.Computer modeling of the effect of perfusion on heating patterns in radiofrequency tumor ablation[J].Int J Hyperther,2007,23(1):49-58.

[38] Abraham JP,Sparrow EM.A thermal-ablation bioheat model including liquid-to-vapor phase change,pressure-and necrosisdependent perfusion,and moisture-dependent properties[J].Int J Heat Mass Tran,2007,50(13):2537-2544.

[39] Trujillo M,Berjano E.Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency ablation[J].Int J Hyperther,2013,29(6):590-597.

[40] Poch FGM,Rieder C,Ballhausen H,et al.The vascular cooling effect in hepatic multipolar radiofrequency ablation leads to incomplete ablation ex vivo[J].Int J Hyperther,2016,32(7):749-756.

[41] Chato JC.Heat transfer to blood vessels[J].ASME J Biomech Eng,1980,102(2):110-118.

[42] Crezee J,Lagendijk JJW.Temperature uniformity during hyperthermia: the impact of large vessels[J].Phys Med Biol,1992,37(6):1321.

[43] Shao YL,Arjun B,Leo HL,et al.A computational theoretical model for radiofrequency ablation of tumor with complex vascularization[J].Comput Biol Med,2017,89:282.

[44] Al-Alem I,Pillai K,Akhter J,et al.Heat sink phenomenon of bipolar and monopolar radiofrequency ablation observed using polypropylene tubes for vessel simulation[J].Surg Innov,2014,21(3):269-276.

[45] Mulier S,Miao Y,Mulier P,et al.Electrodes and multiple electrode systems for radiofrequency ablation: a proposal for updated terminology[J].Eur Radiol,2005,15(4):798-808.

[46] 罗荣光,黄金华.肿瘤射频消融:电极的类型和消融灶的特点[J].介入放射学杂志,2011,20(2):159-162.

[47] Liu CH,Yu CY,Chang WC,et al.Radiofrequency ablation of hepatic metastases: factors influencing local tumor progression[J].Ann Surg Oncol,2014,21(9):3090-3095.

[48] Dodd III GD,Frank MS,Aribandi M,et al.Radiofrequency thermal ablation:computer analysis of the size of the thermal injury created by overlapping ablations[J].Am J Roentgenol,2001,177(4):777-782.

[49] Kang TW,Rhim H.Recent advances in tumor ablation for hepatocellular carcinoma[J].Liver Cancer,2015,4(3):176.

[50] Huang HW.Confluent thermal lesion formation in liver with radio frequency ablation by using internally cooled multipleelectrode technique: Computational results[J].J APPL Sci Eng,2015,18(3):275-288.

[51] Lee ES,Lee JM,Kim WS,et al.Multiple-electrode radiofrequency ablations using Octopus® electrodes in an in vivo porcine liver model[J].Brit J Radiol,2012,85(1017):e609-e615.

[52] Jung L,Min LJ,Jung-Hwan Y,et al.Percutaneous radiofrequency ablation with multiple electrodes for mediumsized hepatocellular carcinomas[J].Korean J Radiol,2012,13(1):34-43.

[53] Soetaert F,Crevecoeur G,Dupre L.Optimizing bipolar radiofrequency ablation treatment by means of pulsed currents[A].Engineering in Medicine and Biology Society(EMBC),2013 35thAnnual International Conference of the IEEE[C].2013:3745-3748.

[54] Mulier S,Jiang Y,Jamart J,et al.Bipolar radiofrequency ablation with 2×2 electrodes as a building block for matrix radiofrequency ablation: Ex-vivo liver experiments and finite element method modelling[J].Int J Hyperther,2015,31(6):649-665.

[55] Shao YL,Leo HL,Chua KJ.Studying the thermal performance of a bipolar radiofrequency ablation with an improved electrode matrix system: In vitro experiments and modelling[J].Appl Therm Eng,2017,116:623-635.

[56] Goldberg SN,Ahmed M,Gazelle GS,et al.Radio-frequency thermal ablation with NaCl solution injection:effect of electrical conductivity on tissue heating and coagulation—phantom and porcine liver study[J].Radiology,2001,219(1):157-165.