云存储环境下可撤销属性加密
王光波 刘海涛 王晨露 王鹏程 练 琳 惠文涛
1(31008部队 北京 100036) 2(61660部队 北京 100036) 3 (61046部队 北京 100094) (691759571@qq.com)
随着大数据时代的到来,出现越来越多的用户数据,为了实现数据共享的同时降低成本,使用第三方的云存储提供商(cloud storage provider, CSP)成为优先选择.云存储作为云计算的延伸与发展,其最大特点是存储即服务,用户可以在任何地点、任何时间,通过任何可连网设备方便地存取数据,因此得到了越来越广泛的应用.但是,云存储中用户数据存储在云端服务器上,脱离了用户的实际控制,因此如何保证用户隐私和数据安全的同时尽可能地提高服务质量已经成为安全云存储的关键问题.
Sahai等人[1]在2005年提出了属性加密(attribute-based encryption, ABE)的概念,将密文和密钥与一系列的属性相关联,通过定义访问结构,指定能够解密数据的属性集合,实现细粒度的访问控制,属性加密方案凭借其灵活的访问结构在云存储中得到了广泛的应用.最初的ABE只能实现门限操作,策略表达不够丰富.因此,有学者提出了基于密文策略[2-4](ciphertext-policy, CP)和密钥策略[5-6](key-policy, KP)的ABE机制,实现丰富的属性操作,因此能够支持更加灵活的访问策略.
然而,在云存储中应用ABE也带来了严重的安全挑战.因为云存储中存在大量的用户,而在ABE的应用中不同的用户可能共享相同的属性.如果用户的某个属性被撤销,如何保证在不影响其他用户正常访问的前提下,实现对该用户相应访问权限的撤销,而且不能造成系统的过载与安全强度的降低,成为亟待解决的问题.本文主要针对这一问题进行研究.
近年来,在ABE的实际应用中,用户撤销的重要性引起了人们的重视,Ostrovsky等人[7]提出了一种实现用户级撤销的ABE方案.该方案通过对撤销用户的身份进行AND的“非”操作来实现撤销,但是性能太差.随后,Staddon等人[8]提出了一种实现用户可撤销的KP-ABE方案,但是该方案只能在满足密文相关属性正好为整个属性集的一半时才能被使用,限制太高,不符合实际应用.Liang等人[9]提出了一种利用二叉树结构来实现用户撤销的CP-ABE方案,由属性授权生成更新密钥实现撤销,但是性能较差,而且增加了属性授权的负担.可以发现,这几种方案都只能实现系统级的用户撤销,即一旦用户的某个属性被撤销,就失去了系统中所有其他属性对应的访问权限.
在属性级用户撤销方面,文献[10-12]通过为每个属性设置有效期来实现属性撤销,但是这种方式不能实现实时撤销.Hur等人[13]提出了一种通过使用密钥加密密钥树来实现属性撤销的CP-ABE方案,该方案能够实现属性级的用户撤销.若某个用户的属性被撤销,CSP将生成新的密钥加密密钥,并重新加密所有的密文.但是,在该方案中,用户需要额外存储lb(nuser+1)长度的密钥加密密钥,其中nuser表示系统内的所有用户,而且该方案仅仅实现了通用群模型下的安全性,通用群模型为启发式的安全,不是可证明安全,很多通用群模型下安全的方案在实际应用中发现并不安全.随后,Yang等人[14]提出了一个适用于云存储环境的CP-ABE方案,该方案为每个属性生成2个对应的公开参数.当需要进行属性撤销时,由属性授权生成更新密钥,并建立安全通道,将其发送给所有未被撤销的用户进行密钥更新,同时发送给CSP进行密文更新.另外,属性授权需要更新该属性对应的2个公钥参数,并将其发送给所有的用户,因此加重了属性授权的计算负载和通信负载.而且,对于每次撤销,用户必须保持在线进行密钥更新和公钥更新.
本文针对这一问题展开研究,提出了一个标准模型下可证明安全的支持属性级用户撤销的CP-ABE方案,在该方案中,一旦用户的某个属性被撤销,CSP将随机选择撤销属性对应的指数,对密文进行更新.然后,本文设计了一个广播属性加密方案对随机指数进行加密,且广播属性加密方案使用与加密算法相同的访问策略.因此,本方案可以实现只有属性集合满足密文访问策略且未被撤销的用户才能进行密钥更新.而且对于每次属性撤销,本文方案的用户不需要进行实时的密钥更新,只有用户解密时才需要进行密钥更新,进而解密密文.而且,用户进行密钥更新前,可以先确认其拥有的属性集合是否满足访问策略,若不满足,则不必进行密钥更新.
1 相关技术
在方案提出前,首先对本文将用到的相关技术进行简单介绍,包括双线性群、线性秘密分享方案及确定性q-parallel BDHE(q-parallel bilinear Diffie-Hellman exponent)假设.
1.1 双线性群
定义1. 双线性群.双线性群提出后被广泛应用到各种密码系统中.令ψ是一个群生成算法,以安全参数λ为输入,输出(p,,T,e).其中p为素数,由安全参数λ决定,和T是2个阶为p的循环群,e:×→T是一个满足3个条件的映射:
1) 双线性.∀u,v∈,a,b∈p,e(ua,vb)=e(u,v)ab.
2) 非退化性.∃g∈使得e(g,g)在T中的阶是p.
3) 计算性.存在有效的对运算算法.
1.2 线性密钥分享方案
定义2. 线性秘密分享方案(linear secret-sharing scheme, LSSS)[15].参与者集合P上的一个秘密共享方案Ⅱ如果满足2个条件,则称为p上的线性秘密共享方案:
2) 对于每个秘密分享方案Ⅱ,存在一个生成矩阵A(l×n),对于矩阵A中的每一行i=1,2,…,l,映射ρ:{1,2,…,l}→P把A的每一行映射到参与者ρ(i).考虑向量v=(s,r2,r3,…,rn),s∈p是共享密钥,r2,…,rn随机选择用来隐藏s,Av是l个秘密份额形成的向量,其中λi=(Av)i表示参与者ρ(i)所持有的秘密份额.
1.3 确定性q -parallel BDHE假设
定义3.q-Parallel BDHE假设[16].令表示阶为p的双线性群,a,s,b1,b2,…,bq为p内随机选择的参数,g为的生成元.若攻击者给定参数
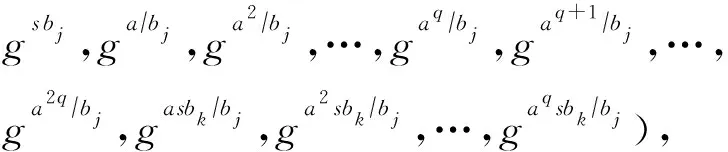
其中,1≤k,j≤q,对攻击者来说,要区别e(g,g)aq+1s与群T中的随机元素R来说是困难的.算法B通过输出z∈{0,1}来进行猜测,定义其拥有优势ε来解决群下的q-Parallel BDHE假设,如果:
|Pr[B(y,T=e(g,g)aq+1s)=0]-
Pr[B(y,T=R)=0]|≥ε,
若无多项式时间算法以不可忽略的优势来解决q-Parallel BDHE问题,那么我们就说假设q-Parallel BDHE在群,T中是成立的.
2 属性加密
本节首先定义了一个标准语义安全的(semantic security)的选择性安全模型,即选择明文攻击下的密文不可区分性(ciphertext indistinguishability under chosen plaintext attacks, IND-CPA)[17];接着对本文提出的属性加密方案进行构造.
2.1 选择性安全模型
在该选择性安全模型中,我们将使用Tu等人[18]提出的技术,其具体定义如下:
1) 选择阶段.攻击者A选择将要攻击的访问结构A*与属性x*的撤销列表RLx*.
2) 参数设置阶段.挑战者B运行初始化Setup算法,并把产生的系统公开密钥参数PK发送给攻击者A.
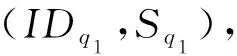

4) 挑战阶段.攻击者A提交长度相等的2个消息M0与M1给挑战者B.然后B随机选择β∈{0,1},并在访问结构A*下加密Mβ,产生密文CT*,并将其发送给攻击者A.
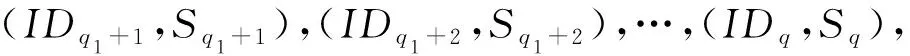
6) 猜测阶段.攻击者A输出一个值β′∈{0,1}作为对β的猜测.如果β′=β,我们称攻击者A赢得了该游戏.攻击者A在该游戏中的优势定义为
AdvA=|Pr[β′=β]-12|.
若无多项式时间算法以不可忽略的优势来攻破以上安全模型,那么我们就说本文提出可撤销属性加密方案是安全的.
2.2 方案构造
本节对提出的可撤销属性加密方案进行了具体构造.
2.2.1 系统初始化
系统初始化阶段,属性授权生成系统的相关参数,包括公开密钥与主密钥.
初始化算法:Setup(λ,U,n)→(PK,MSK).
属性授权以安全参数λ、属性集合U与用户数量n作为输入,运行群生成函数ψ获得系统参数(p,,T,e),其中p为素数,和T是p阶循环群,e是一个双线性映射.g∈为群的生成元.算法随机选择α,β∈p,并且设置gi=g(αi)∈,其中i=1,2,…,n,n+2,n+3,…,2n.接着算法随机选择γ∈p,设置v=gγ.对于每一个属性i∈U,算法随机选择参数h1,h2,…,hU∈.系统公开密钥参数PK设置为
PK=(p,g,g1,g2,…,gn,gn +2,gn +3,…,
g2n,v,e(g,g)β,h1,h2,…,hU),
主密钥MSK设置为
MSK=(α,γ,gβ).
2.2.2 数据加密
当用户想要将数据M放到CSP时,他首先定义访问控制策略(A,ρ),其中A是一个l×n矩阵,映射函数ρ把A的每行Ai映射到一个属性ρ(i).如文献[19]要求ρ不会把2个不同的行映射到同一个属性.然后运行算法Encrypt(PK,M,(A,ρ))对M进行加密.
加密算法:Encrypt(PK,M,(A,ρ))→CT.
算法以系统公开密钥PK、明文消息M和访问控制策略(A,ρ)为输入,然后算法随机选择s,v2,v3,…,vn∈p,并定义向量v=(s,v2,v3,…,vn),对A的每一行Ai,计算内积λi=Ai·v,并随机选择ri∈p,算法输出密文:
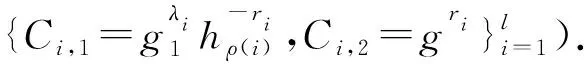
2.2.3 数据重加密
当用户集RLx的属性x被撤销时,为了撤销该属性对应的访问权限,但不影响该用户集其他属性以及其他用户的正常访问,使用广播属性加密对密文进行更新.
重加密算法:Re_encrypt(PK,CT,RLx)→CT″.
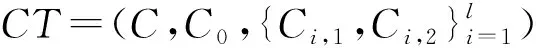
因此最后输出密文为CT″=(CT′,Hdrx).
2.2.4 密钥生成
为了实现外包解密、提高性能,生成密钥:
密钥生成算法:KeyGenout(PK,MSK,ID,S)→SK.
算法以系统公开密钥PK、主密钥MSK、用户身份ID和用户属性集合S为输入,然后算法随机选择参数r′∈p,并生成相应的用户密钥其中:
密钥生成后,算法随机选择参数z∈*p,并计算:
K=(K′)=(gαIDγ)(gα r′),
L=(L′)=(gr′),
令r=r′z,得到密钥为
2.2.5 部分解密
为了实现用户的外包解密,用户需要将外包密钥TK发送给CSP,然后CSP代为进行部分解密如下:
部分解密算法:Transformout(TK,CT″)→TCT.
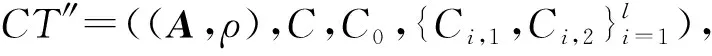
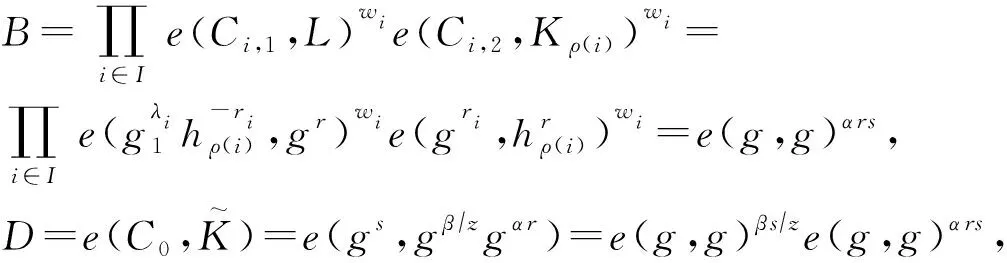
部分解密完成后,CSP将TCT=(C,E)发送给用户进行最后解密.
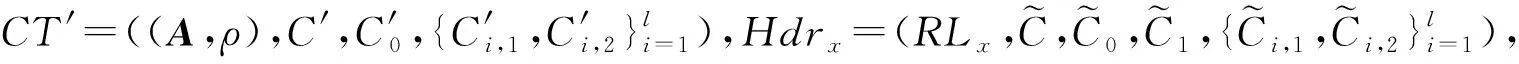
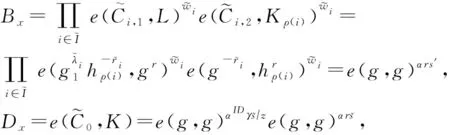
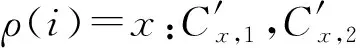
2.2.6 解密
用户得到部分解密密文后,进行最后解密.
解密算法:Decrypt(TCT,SK)→M.
算法以部分解密密文TCT与用户密钥SK为输入.
1) 无属性被撤销,即TCT=(C,E).此时用户计算:
CEz=M×e(g,g)β s(e(g,g)β sz)z=M.
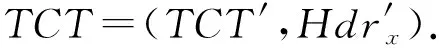
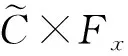
若用户属性集合S满足访问策略(A,ρ),则CSP能在多项式时间计算{wi∈p}i∈I使成立,然后计算:
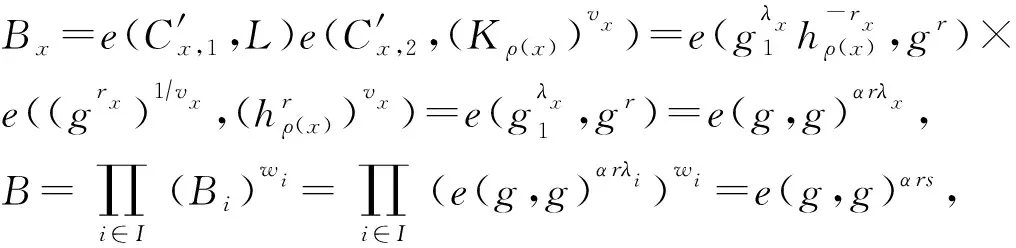
2.3 安全证明
引理1. 若确定性的q-parallel BDHE假设在群与T中成立,那么没有多项式时间的攻击者能选择性地攻破我们的方案,其中挑战矩阵为A*(l*×n*),且l*,n*≤q.
证明. 假设攻击者A能以不可忽略的优势ε=AdvA选择性地攻破我们的方案,而且假设其挑战矩阵为A*(l*×n*),且l*,n*≤q.接下来,我们将构造仿真器B来攻破确定性的q-parallel BDHE假设.
1) 选择阶段.仿真器B以确定性的q-parallel BDHE挑战y,T为输入.并且攻击者A给定访问控制(A*,ρ*)与属性x*的撤销列表RLx*,其中A*有n*列.
2) 参数设置阶段.仿真器B随机选择β′∈p,并通过计算e(g,g)β=e(g,g)β′×e(gα,gαq)来隐含地设置β=β′+αq+1.另外算法设置广播集:
然后选择u∈p,并设置
设置群元素h1,h2,…,hU,对于每个x(1≤x≤U),随机选择参数zx∈p.令X表示ρ*(i)=x的索引i的集合,因此hx被设置为
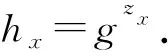
最后仿真者B发送给攻击者A公开密钥为
PK=(g,g1,g2,…,gq,gq+2,gq+3,…,
g2q,v,e(g,g)β,h1,h2,…,hU).
3) 查询阶段1. A向B进行密钥生成查询Okg与密文重加密查询Oree.
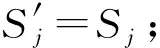
仿真器B计算向量w=(w1,w2,…,wn*)∈np,
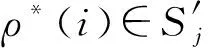
仿真器随机选择t∈p,并定义r为
r=t+w1αq+w2αq-1+…+wqα.
计算L′为
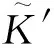

密钥生成后,B随机选择参数z∈*p,并且设置外包密钥:
私钥SK=(z,TK),最后将TK发送给A.
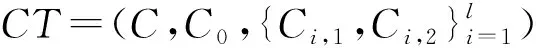
仿真器随机vx*∈*p,并输出重加密密文:
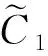
因此,最终生成重加密密文为
CT″=(CT′,Hdrx*).
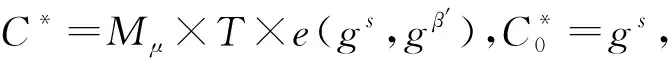
5) 查询阶段2. 如查询阶段1,A向B进行密钥生成查询Okg与密文重加密查询Oree.
6) 猜测阶段.攻击者A最终输出对μ的猜测μ′.若μ=μ′,A输出0表示猜测T=e(g,g)αq+1s;否则输出1表示猜测T为群T中的随机元素.
若T=e(g,g)αq+1s,那么CT′为有效密文,因此得出:
而当T为群T中的随机元素时,Mμ对于攻击者来说是完全随机的,得出:
因此,B能以不可忽略的优势模拟确定性的q-parallel BDHE假设.
证毕.
3 方案分析与实验验证
现将本文提出的方案与已有3种撤销方案进行对比,包括功能性、存储成本、通信成本与计算性能.其中所使用的描述符如下:|C1|表示中数据元素的长度;|CT|表示T中数据元素的长度;|Cp|表示*p中数据元素的长度;CT表示密文中访问结构的元素个数;|Ck|表示Hur方案中使用的密钥KEK的长度;t表示与密文有关的属性个数;k表示用户密钥中属性的个数;nattr表示整个系统中属性的总个数;nuser表示整个系统中用户的总个数;nra表示系统中撤销属性的个数;nru表示撤销用户的个数;nmax表示Liang方案中密文访问结构的最大列向量.
3.1 功能说明
从表1可以看出,Liang方案实现了系统级的用户撤销,一旦用户的某个属性被撤销,该用户就失去了系统内所有其他合法属性的访问权限,这不符合实际的环境应用.而本文方案、Hur方案和Yang方案都实现了属性级的用户撤销,即若用户的某个属性被撤销,不会影响该用户其他合法属性的正常访问.但是,Hur方案只实现了一般群模型下的可证明安全性,Yang方案则只实现了随机预言模型下的可证明安全性,而很多一般群模型和随机预言模型下可证明安全的方案在实际应用中被发现并不安全.相对于Hur方案和Yang方案,本文在标准模型下基于q-parallel BDHE假设对方案的安全性进行了完整的证明,实现了更高的安全性.
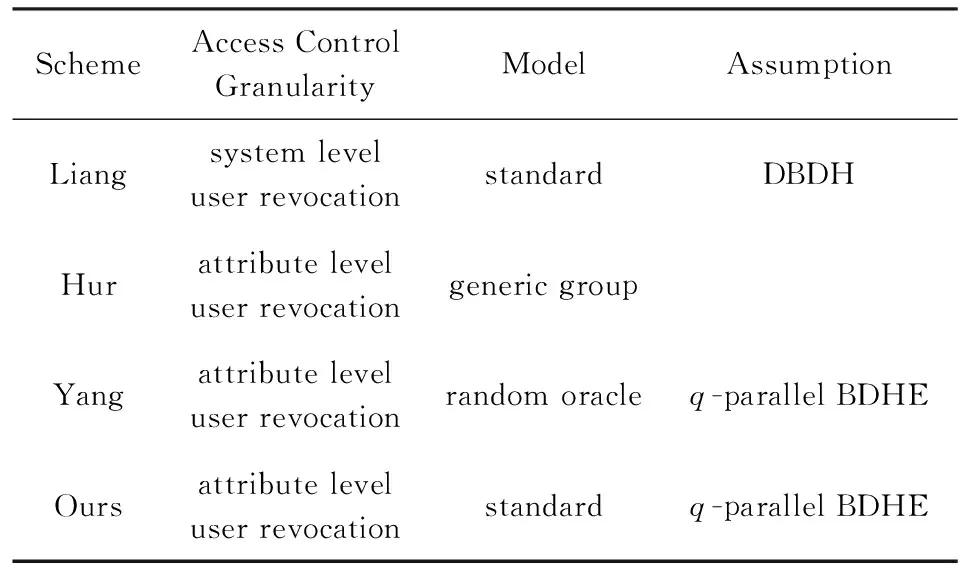
Table 1 Comparison of Function表1 功能对比
3.2 存储成本
表2将本文方案与其他相关方案进行了存储成本的对比.属性授权AA的存储成本主要来自于主密钥,我们的方案与Hur方案使用了较少的主密钥.而Liang方案中,主密钥随着用户总数nuser呈线性增长,Yang方案则随着属性总数nattr呈线性增长.数据拥有者O的存储成本主要来自于公钥.Hur方案使用了最少的公钥,Yang方案公钥随着属性总数nattr呈线性增长,Liang方案公钥随着属性总数nattr与访问矩阵列向量CTt呈互为斜率的线性增长,而本文方案中,公钥随着属性总数nattr与用户总数nuser呈斜率为常数的线性增长.云存储提供商CSP的存储成本主要来自于密文与密文头.因为Liang方案只实现了用户撤销,在该方案中,利用子集覆盖进行密钥更新,不需要对密文进行更新,但其密文长度随着访问结构CT呈线性增长.Yang方案通过属性授权与用户交互为用户进行密钥更新,并对被撤销属性对应的密文进行更新,因此,密文长度只与密文相关属性个数t呈线性增长.Hur方案中,数据拥有者将密文发送给CSP后,CSP为每个属性组生成相应的密文头,因此其存储包括密文及密文头,其密文长度与密文相关属性个数t呈斜率为常数的线性增长,而密文头长度与密文相关属性个数t及用户总数nuser呈互为斜率的线性增长.本文方案中,若发生属性改变,CSP为该属性对应的密文重新选择指数进行密文更新,并将指数进行加密,生成相应的密文头.因此其存储也包括密文及密文头,且密文随着密文相关属性个数t呈线性增长,密文头则随着密文相关属性个数t及撤销属性个数nra呈互为斜率的线性增长.数据访问者的存储成本主要来自于其拥有的密钥.本文方案与Yang方案中,密钥长度较短,只与用户拥有的属性个数k呈线性增长;Liang方案利用二叉树来生成用户密钥,其密钥长度与密钥属性个数k、密文访问结构最大列向量nmax与用户个数nuser都相关.而属性撤销时,使用子集覆盖进行密钥更新,其更新密钥长度与最小覆盖集呈正增长.而Hur方案中,每个用户都要存储一定的KEK来解密相应的指数进行密钥更新,因此其密钥长度不仅与用户拥有的属性个数k呈线性增长,而且与整个系统中用户的总个数nuser呈对数增长.
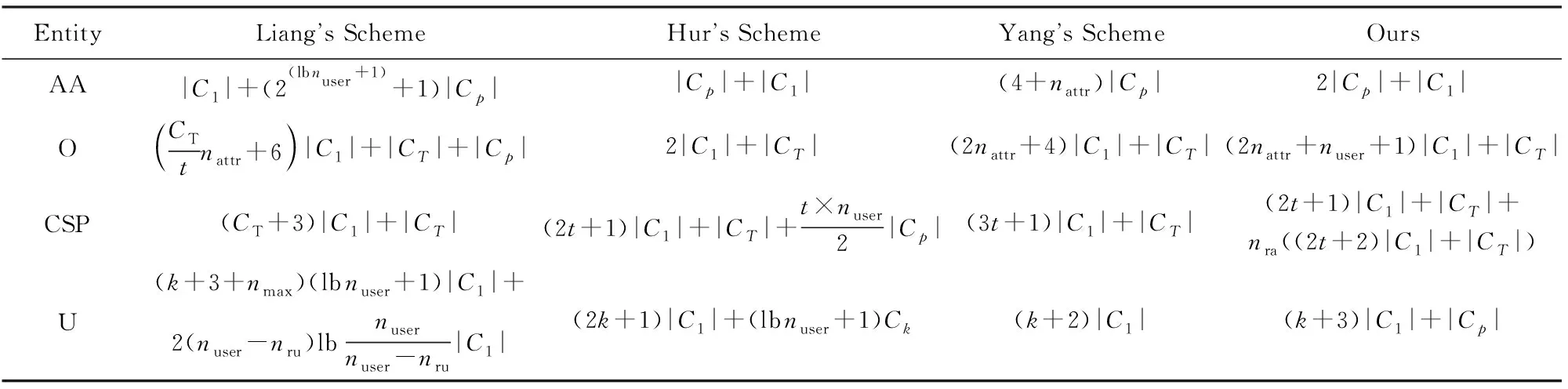
Table 2 Comparison of Storage Cost表2 存储成本对比
3.3 通信成本
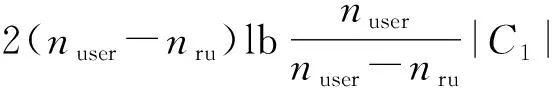
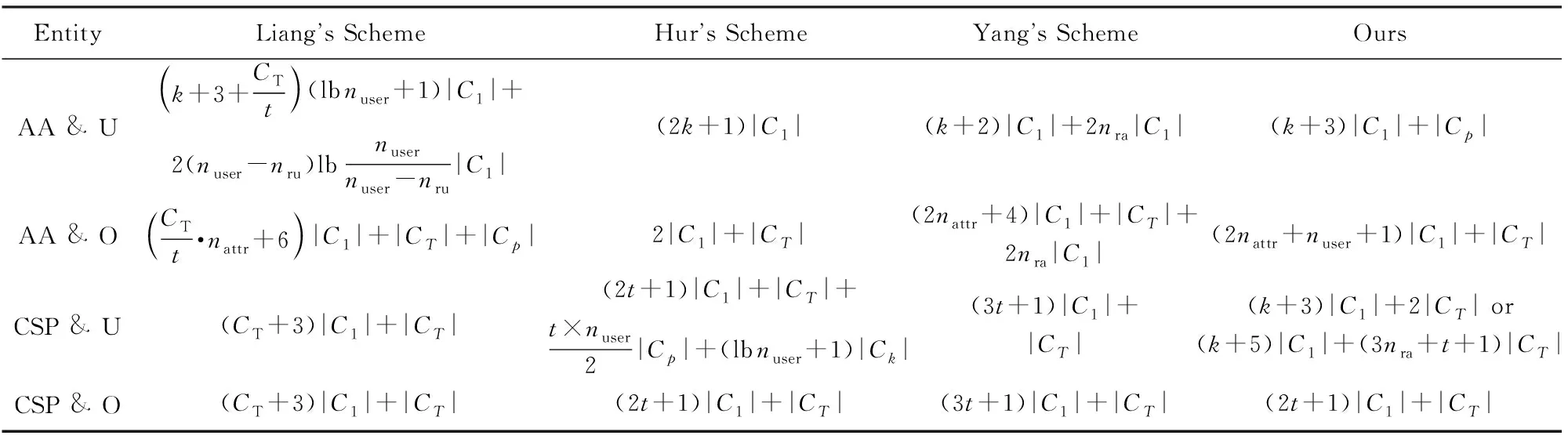
Table 3 Comparison of Communication Cost表3 通信成本对比
3.4 计算性能
实验环境为64 b Ubuntu 14.04操作系统、Intel®CoreTMi7-3770CPU(3.4 GHz)、内存4 GB,实验基于Pairing-based Cryptography Library(PBC-0.5.14)[20]与cpabe-0.11[21]进行修改与编写,并且使用基于512 b有限域上的超奇异曲线y2=x3+x中的160 b椭圆曲线群.实验数据取运行20次所得的平均值.在实验中,PBC库计算对运算的时间大约为5.3 ms,1与T的运算时间大约为6.2ms与0.6ms.另外,通过使用Ubuntu14.04操作系统中的devurandom来选择1与T中随机元素的时间大约为14 ms与1.4 ms.
本文对4种方案在密钥生成时间、加密时间、解密时间与重加密时间方面进行了比较,并且取nmax=6,nuser=10.
如图1所示,密钥生成时间与用户属性个数呈线性增长,本文方案密钥生成时间略高于Yang方案,但优于Hur方案与Liang方案.特别是Liang方案,其密钥生成时间不仅与用户属性个数有关,而且与密文访问结构最大列向量nmax与用户个数nuser相关,因此其密钥生成时间远远大于其他3种方案.
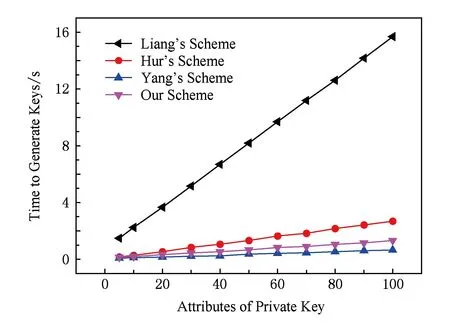
Fig. 1 Key generation time图1 密钥生成时间
如图2所示,加密时间与访问结构中的属性呈线性增长.本文方案加密时间略高于Hur方案,但优于Yang方案与Liang方案.需要注意的是,Hur方案加密过程中,中间节点的多项式操作涉及了适当数量的乘法,但是运行时间很短;而Liang方案其加密生成时间不仅与访问结构中的属性个数有关,而且同样与访问结构最大列向量nmax相关,因此加密时间远远大于其他3种方案.进行解密实验时,使用所用的属性进行解密,并且对Hur方案进行解密时使用最简单的二叉结构,所有中间节点均为(n,n)门限.而本文提出的方案分别在无属性撤销与50%的属性被撤销2种情况下进行了解密实验.
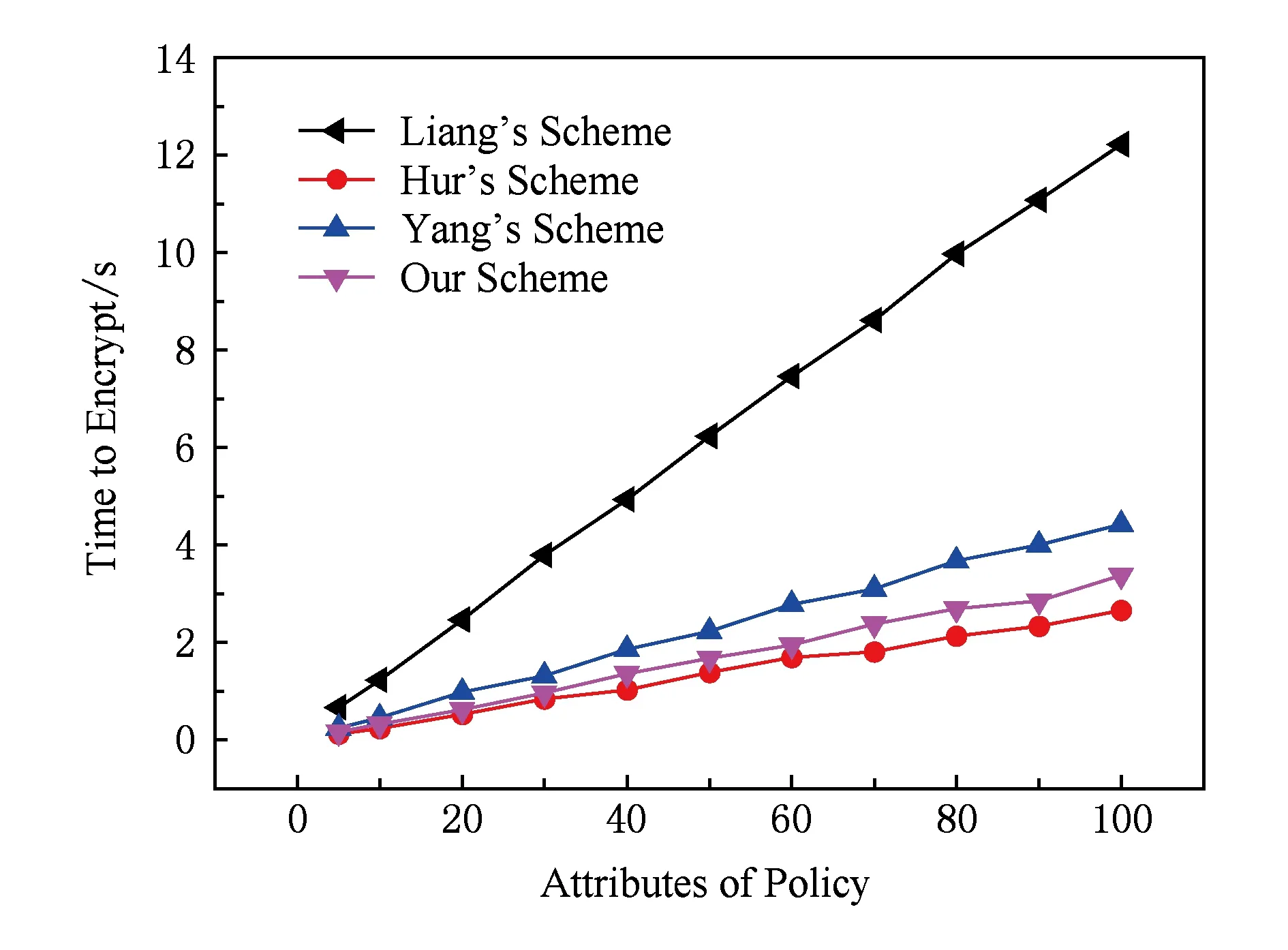
Fig. 2 Encryption time图2 加密时间
如图3所示,Liang方案、Hur方案、Yang方案与本文50%属性被撤销方案的解密时间都随着解密属性数量而增长,而本文无属性撤销方案由于采用了外包解密,其用户只需要进行1个T的指数操作.另外,由于本文属性撤销方案的解密时间为解密属性的二次函数,但是本文采用了外包解密,大大降低了用户的解密时间.图3可以看出,当属性在某个范围内时,本文撤销方案的解密时间小于其他方案,随着属性个数的增加,其解密时间逐次超过Yang方案与Hur方案,但在可接受的范围.为了进行重加密时间对比,不失一般性,本文考虑了用户数量为10的情况下重加密时间与属性数量的关系和属性数量为10的情况下重加密时间与用户数量的关系.
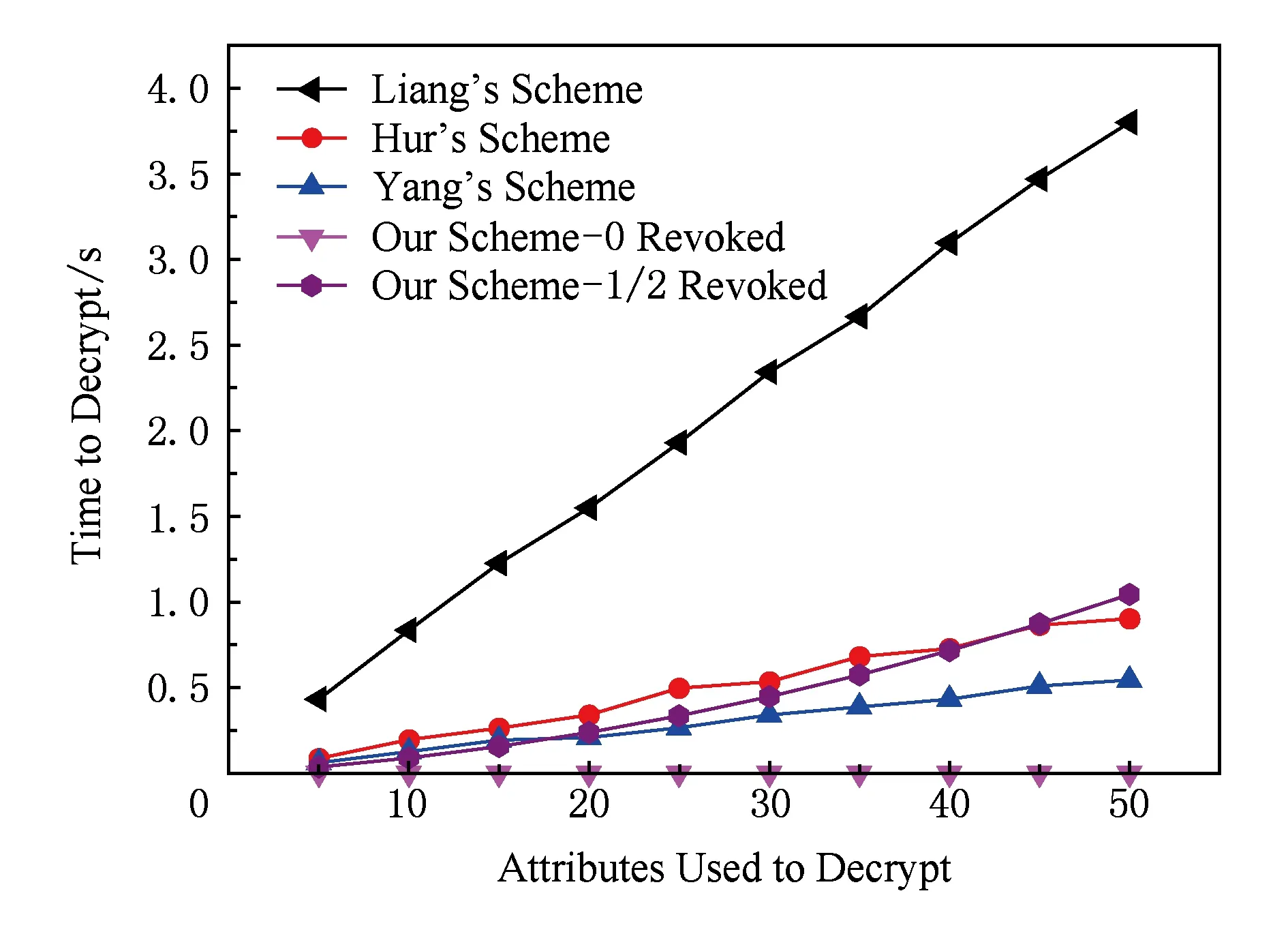
Fig. 3 Decryption time图3 解密时间
如图4所示为用户数量为10的情况下重加密时间与属性数量的关系,当属性被撤销时,需要对密钥或密文进行更新.Yang方案与Liang方案主要对密钥进行更新,而Hur方案与本文方案主要对密文进行更新.因此从图4中可以发现,Hur方案与本文方案需要的计算时间较长,且随着属性数量逐渐增长,但是所需计算完全是由CSP实施的,实际应用中CSP拥有大量的计算资源;而Yang方案与Liang方案虽然需要的计算时间较少,但是需要AA实施密钥更新,而AA的计算资源是有限的,容易造成系统瓶颈.
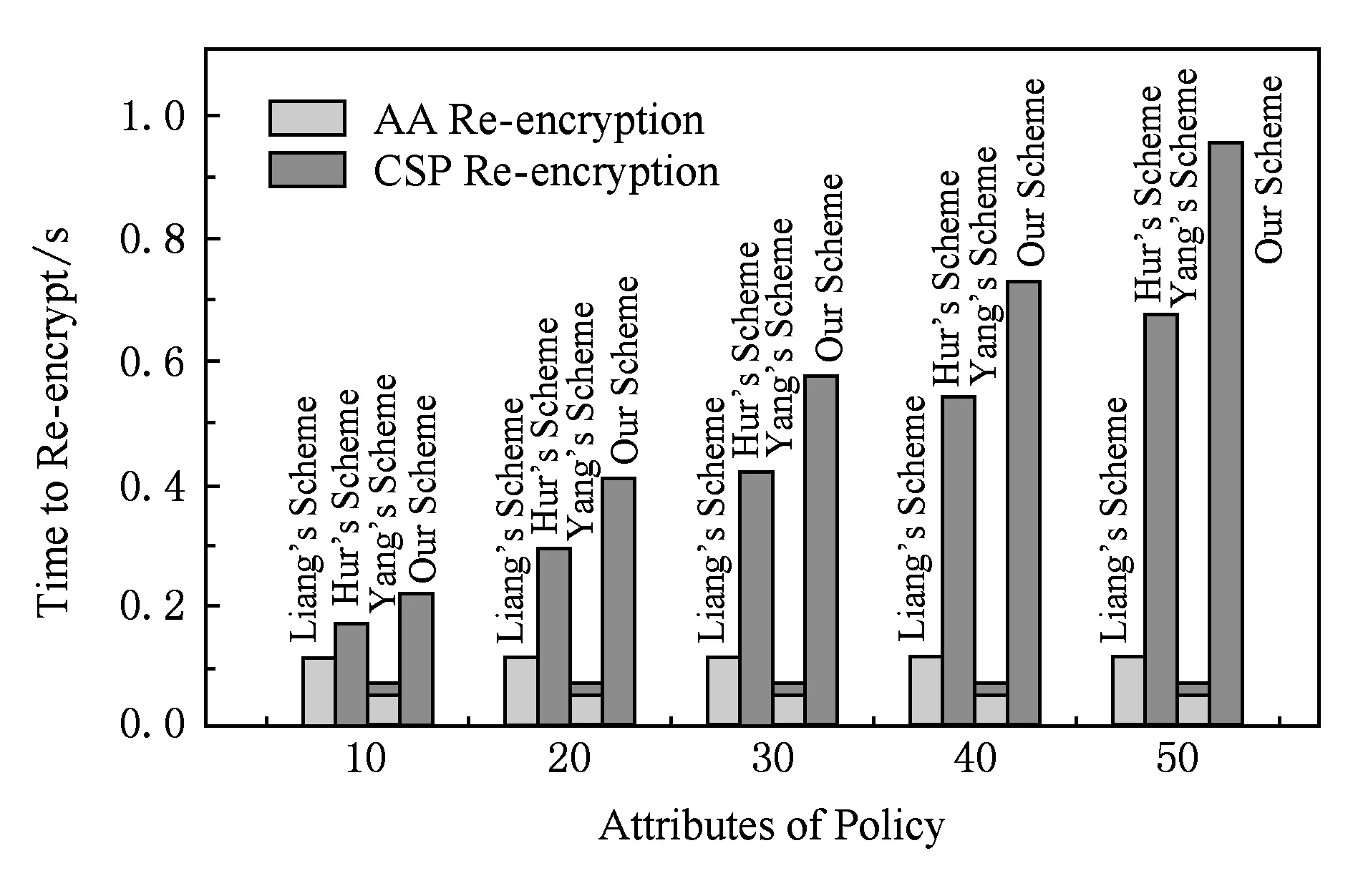
Fig. 4 Re-encryption time图4 重加密时间
如图5所示为属性数量为10的情况下重加密时间与用户数量的关系.从图5中可以发现,Liang方案、Hur方案和本文方案的重加密时间与用户个数无关;而在Yang方案中,一旦发生属性撤销,AA需要为所有未被撤销的用户进行解密密钥更新,加重了AA的计算负载.
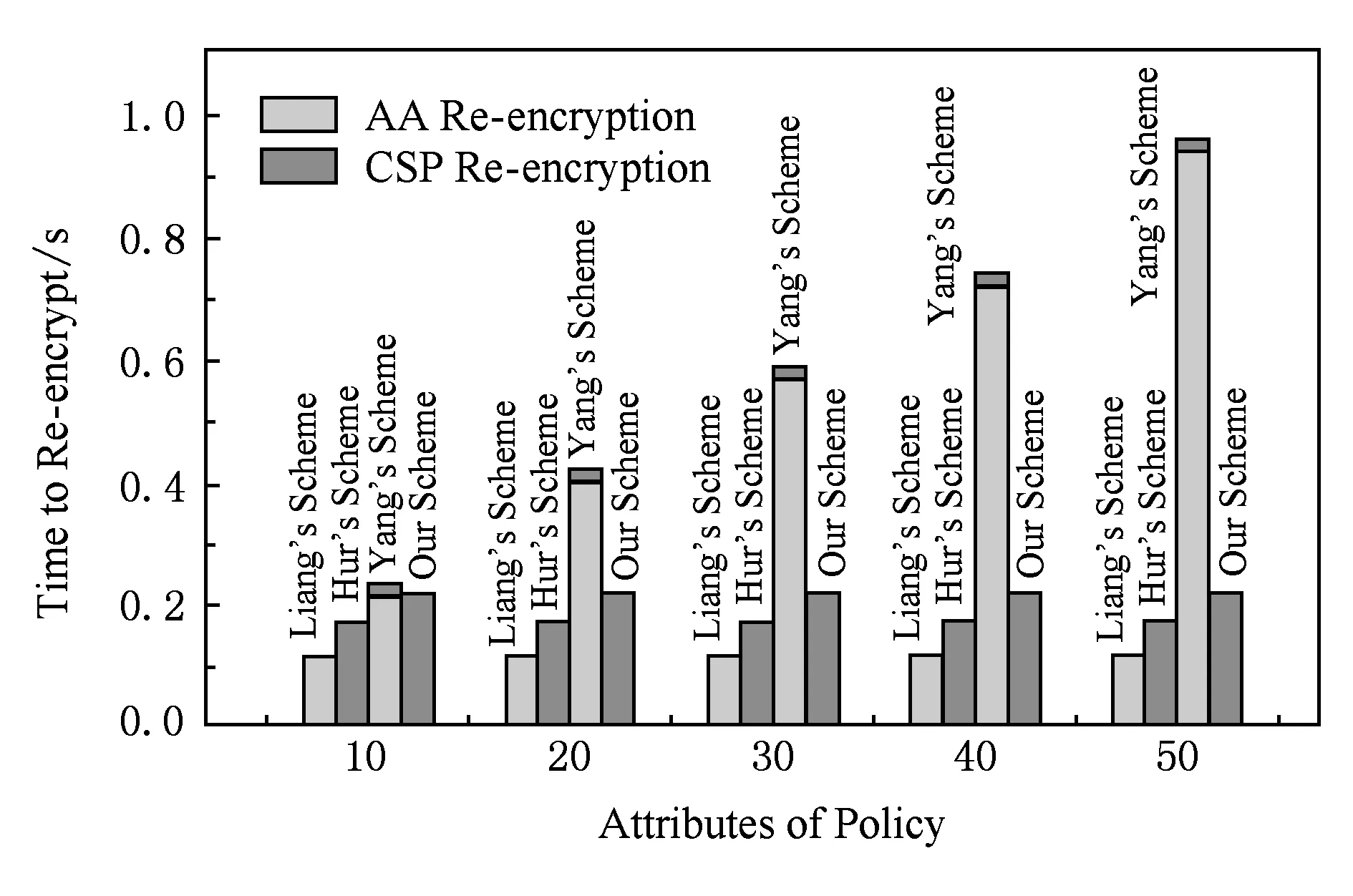
Fig. 5 Re-encryption time图5 重加密时间
4 总 结
本文提出了一个密文策略的属性加密方案,该方案能够实现属性级的用户撤销.在该方案中,若用户的属性被撤销,那么对该属性对应的密文进行更新,只有属性满足访问策略且没有被撤销的用户才能够成功地进行密钥更新,而成功解密密文.本文基于q-parallel BDHE假设在标准模型下对方案进行了选择访问结构明文攻击的安全性证明.最后对方案进行了性能分析与实验验证,实验结果表明,与已有相关方案相比,虽然为了实现属性撤销,增加了存储中心的计算负载,但是不需要属性授权的参与,因此降低了属性授权的计算负载,而且用户除了密钥外不需要其他额外参数来实现属性撤销,因此大大节省了存储空间.另外本文基于q-parallel BDHE假设,在标准模型下对方案进行了选择访问结构明文攻击下的安全性证明,该方案可以通过文献[22]中提出的通用技术转换为选择访问结构密文攻击下可证明安全的方案,以适用于云存储环境下用户数据多以密文形式存储的情形.
[1]Sahai A, Waters B. Fuzzy Identity-Based Encryption[M]. Berlin: Springer, 2005: 457-473
[2]Yadav U C. Ciphertext-policy attribute-based encryption with hiding access structure[C]Proc of the 5th IEEE Int Advance Computing Conf (IACC). Piscataway, NJ: IEEE, 2015: 6-10
[3]Naruse T, Mohri M, Shiraishi Y. Provably secure attribute-based encryption with attribute revocation and grant function using proxy re-encryption and attribute key for updating[J]. Human-centric Computing and Information Sciences, 2015, 5(1): 8
[4]Wang Hao, Yang Bo, Wang Yilei. Server aided ciphertext-policy attribute-based encryption[C]Proc of the 29th IEEE Int Conf on Advanced Information Networking & Applications Workshops. Piscataway, NJ: IEEE, 2015: 440-444
[5]Li Qi, Ma Jiangfeng, Li Rui, et al. Large universe decentralized key-policy attribute-based encryption[J]. Security & Communication Networks, 2015, 8(3): 501-509
[6]Wang Xinlei, Zhang Jianqing, Schooler E M, et al. Performance evaluation of attribute-based encryption: Toward data privacy in the IoT[C]Proc of the 26th Int Conf on Communications (ICC). Piscataway, NJ: IEEE, 2014: 725-730
[7]Ostrovsky R, Sahai A, Waters B. Attribute-based encryption with non-monotonic access structures[C]Proc of the 14th ACM Conf on Computer & Communications Security (CCS). New York: ACM, 2007: 195-203
[8]Staddon J, Golle P, Gagn M, et al. A content-driven access control system[C]Proc of the 7th Symp on Identity and Trust on the Internet. New York: ACM, 2008: 26-35
[9]Liang Xiaohui, Lu Rongxing, Lin Xiaodong. Ciphertext policy attribute based encryption with efficient revocation[J]. IEEE Symp on Security & Privacy, 2008, 6(3): 321-334
[10]Bethencourt J, Sahai A, Waters B. Ciphertext-policy attribute-based encryption[C]Proc of the 28th Symp on Security and Privacy. Los Alamitos, CA: IEEE Computer Society, 2007: 321-334
[11]Boldyreva A, Goyal V, Kumar V. Identity-based encryption with efficient revocation[C]Proc of the 15th ACM Conf on Computer and Communications Security(CCS). New York: ACM, 2008: 417-426
[12]Pirretti M, Traynor P, Mcdaniel P, et al. Secure attribute-based systems[C]Proc of the 13th ACM Conf on Computer and Communications Security(CCS). New York: ACM, 2006: 799-837
[13]Hur J, Noh D K. Attribute-based access control with efficient revocation in data outsourcing systems[J]. IEEE Trans on Parallel & Distributed Systems, 2011, 22(7): 1214-1221
[14]Yang Kan, Jia Xiaohua, Ren Kui. Attribute-based fine-grained access control with efficient revocation in cloud storage systems[C]Proc of the 8th ACM SIGSAC Symp on Information, Computer and Communications Security. New York: ACM, 2013: 523-528
[15]Zavattoni E, Perez L J D, Mitsunari S, et al. Software implementation of an attribute-based encryption scheme[J]. IEEE Trans on Computers, 2015, 64(5): 1429-1441
[16]Waters B. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization[C]Proc of the 14th Int Workshop on Public Key Cryptography. Berlin: Springer, 2011: 53-70
[17]Cheung L, Newport C. Provably secure ciphertext policy ABE[C]Proc of the 14th ACM Conf on Computer and Communications Security. New York: ACM, 2007: 456-465
[18]Tu Shanshan, Niu Shaozhang, Li Hui. A fine-grained access control and revocation scheme on clouds[J]. Concurrency & Computation Practice & Experience, 2012, 28(6): 1697-1714
[19]Lewko A, Okamoto T, Sahai A, et al. Fully Secure Functional Encryption: Attribute-based Encryption and (Hierarchical) Inner Product Encryption[M]. Berlin: Springer, 2010: 62-91
[20]Lynn B. The pairing-based cryptography (PBC) library[OL]. 2006 [2015-06-06]. http:crypto.stanford.edupbc
[21]Bethencourt J, Sahai A, Waters B. Advanced crypto software collection: The cpabetoolkit[OL]. 2011 [2015-06-06]. http:acsc.cs.utexas.educpabe
[22]Yamada S, Attrapadung N, Hanaoka G, et al. Generic constructions for chosen-ciphertext secure attribute based encryption[C]Proc of the 14th Int Conf on Practice and Theory in Public Key Cryptography. Berlin: Springer, 2011: 71-89

WangGuangbo, born in 1987. PhD. Engineer. His main research interests include cryptograph theory especially attribute-based encryption.

LiuHaitao, born in 1980. Master. Engineer. His main research interests include computer software and theory.

WangChenlu, born in 1990. Graduate. Assistant Engineer. Her main research interests include network security.
WangPengcheng, born in 1990. Graduate. Assistant Engineer. His main research interests include network security.

LianLin, born in 1990. Master. Engineer. Her main research interests include information security.

HuiWentao, born in 1990. Master. Engineer. His main research interests include network security.

