基于MATTLAB的CT系统参数标定与图像重建
黄佰凡 徐峰远 宋根龙 李飞翔


摘要:在工程中经常遇到如人体内脏、地下矿藏等无法直觀测量分析的问题,而图像重建就是利用X射线或超声波透过被遮挡物体得到多组的透视数据,恢复物体的断层图。文章根据图像重建算法在CT系统中的运用实现,对未知介质的分布进行分析。
关键词:CT系统;参数标定;Radon变换;图像重建
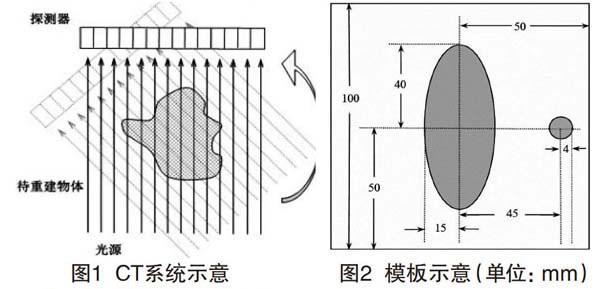
由于电子计算机断层扫描(Computed Tomography,CT)系统安装时容易存在误差,从而影响成像质量,因此,需要对安装好的系统参数进行标定,也就是通过借助已知结构的样品来标定CT系统的参数,并对未知样品进行成像重建。 典型的二维CT系统,其平行入射的X射线垂直于探测器平面,将每个探测器单元看成一个个等距排列的接收点。CT系统的发射器和探测器的相对位置固定不变,让整个发射一接收系统围绕某一固定旋转中心逆时针旋转180次,每次旋转1。。固定二维待检测介质不动,对每一个X射线方向或路径,让包含512个等距单元的探测器测量吸收衰减后的射线能量,经过处理后得到180组接收信息。CT系统示意如图l所示。
由于CT系统安装时容易存在误差,从而影响成像质量,因此需要对安装好的系统参数进行标定,也就是通过借助己知结构的样品来标定CT系统的参数,并对未知样品进行成像重建。
1 模型建立
如图2所示,将两个均匀固体介质组成的标定模板放置在正方形托盘上,得到180组模板几何信息和接收信息,确定CT系统旋转中心在正方形托盘中的位置。
1.1探测器单元之间的距离
我们发现,照射小圆和椭圆的投影是先分离后重合的,选取小圆与椭圆分离时候的小圆投影探测器的数据,利用86个方向上的小圆直径投影所占探测器单元的个数,对其求平均值,得到投影总宽度:d,=28.835 3,由于旋转过程中小球直径一定,为8 mm,可求探测器单元之间的距离:L=d/d得出单个探测器长度即探测器单元之间的距离/=0.277 4 mm。
1.2 CT系统旋转中心的位置
建立如图3所示直角坐标系,规定坐标系不动,而CT坐标系围绕实际旋转中心O'逆时针旋转θ的情形,可见理想旋转中心与实际现转中心存在y轴偏移量和x轴偏移量。
1.2.1 y轴偏移量
当旋转到水平位置时,CT系统的X射线由右向左射入,此时椭圆在探测器上的投影部分长度恰好为椭圆的长轴长度,可以求解得出此时椭圆圆心的位置。己知,由于理想的旋转中心应该处在垂直于探测器单元第256个探测器上的射线,然后根据推导公式:
可得y轴偏移量Pv。这里,Y1表示椭圆最低点所对应的探测器的位置,y2表示椭圆最高点所对应的探测器的位置,则求出y轴的偏移量为
1.2.2 x轴偏移量
利用MATLAB软件分析,如图4所示。由图可知,在旋转次数达到140次时,图像出现波谷,则代表此时X射线是由上向下照射,此时小圆和椭圆在探测器上的投影不重合。
根据椭圆跟小圆在探测器上的投影长度,求得小圆圆心的投影位置。得出小圆圆心在探测器的位置区间为[59,60],约第59.855 6个探测器的单元位置处。根据小圆圆心到理想旋转中心的距离函数关系:
以及时由偏移量与小圆直径的关系:
可以得出X轴的偏移量为
1.3旋转中心结果
综合x轴偏移量和y轴偏移量,如图5所示,可以得出CT系统旋转中心的位置坐标(- 9.417 9,5.548 8)。
2 图像重建模型建立
为了确定未知介质在正方形托盘中的位置,需要将探测器得到的投影数据转换成原始图像数据,即图形的重建过程,而Radon逆变换就是根据一套完整的投影数据,对原始图像重建的严谨算法,同时投影数据的获得又无须深入物体内部。得到原始图像后,图片的灰度值变化规律呈现了吸收率的变化规律。
2.1 Radon变换
Radon变换是调和分析与积分几何领域中的重要课题,从分析学的角度看,研究积分变换的目的是通过把某些问题从原来的框架转移到一个新的框架中,从而将在初始的情形下把难处理的问题表现形式转化为易处理的形式,然后再用积分逆变换转换到原来的框架中‘1]。
下面简要说明R2上的重构图形的思路,固定臼,将Rf(t,臼)变换(关于t)为:
这表明对图形投影Rf(t,θ)等同于对图像,b∽的二维变换,称为中心切片定理,图形重构就是求投影Rf(t,臼)的逆变换(反演变换),因此, (。cos臼,m sin口)作傅里叶逆变换,从而得到Radon变换的逆变换为:
2.2 MATLAB图像重组部分参考程序
information= load(‘shuju.dat);
%导入未知介质吸收信息
[img3,h3]=iradon(information,[0: 179]+st art_angre);%Radon逆变换重建二维图像
n= size(img3,1);
[x,y]=meshgrid([-n/2:n/21*l);
2.3 MATLAB图像重组实现结果
利用MATLAB中的Radon逆变换,将两组数据导入后得出未知介质在正方形托盘中分布的图像,如图6-7所示。
3结语
本文通过已有数据对横纵偏移量的讨论,实现了对CT系统的参数标定,并给出MATLAB程序,通过Radon逆变换完成了探测器数据的图像重建。

