基于旋量的4UPS/UPR并联机构动力学建模及分析*

耿明超，边 辉，刘春东,，李 欣

(1.河北建筑工程学院 机械工程学院，河北 张家口 075000；2.燕山大学 河北省并联机器人与机电系统实验室，河北 秦皇岛 066004)

0 引言

并联机构具有结构紧凑、承载能力强、累积误差小等优点，广泛应用于并联机床、运动模拟器等领域。动力学模型是机构优化设计及控制的基础。随着制造业的转型升级，机构构型更加复杂、负载更大、速度更快，这也对机构的动力学建模及分析提出了更高的要求。

并联机构的动力学建模方法主要有以牛顿-欧拉公式为代表的矢量力学方法[1-2]和以拉格朗日方程为代表的分析力学方法[3-4]。上述方法一般使用两个三维矢量来表示刚体的转动和移动，导致其运动学、动力学建模过程繁琐复杂，且极易出错。旋量代数以其对刚体空间运动描述的几何直观性与代数抽象性而备受机构学者的欢迎。李泽湘等[5]基于旋量及其伴随变换建立了机器人的动力学方程，揭示了李群、李代数在机器人学中的应用。郭菲等[6]基于旋量键合图建立了3-UPS/S机构的动力学模型。Gallardo等[7]利用旋量代数及虚功原理建立了并联机构的动力学模型，其推导过程中需要得到刚体质心点的速度、加速度，旋量建模的优越性并没有得到较好的体现。Sugimoto[8]利用影响系数矩阵和环矩阵建立了并联机构的动力学模型，但其推导过程仍比较复杂，尤其是对于多环路的机构。

本文以4UPS/UPR少自由度并联机构为研究对象，基于旋量代数建立其动力学模型，在此基础上给出了描述机构动力学特性的动力学耦合指标。

1 4UPS/UPR并联机构机构描述

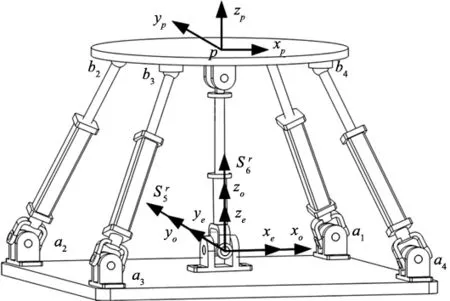
图1 4UPS/UPR并联机构构型

如图1所示，4UPS/UPR并联机构包含4个驱动分支(UPS分支)和一个中间约束分支(UPR分支)。4个驱动分支由万向铰(U)、移动副(P)和球副(S)组成。中间约束分支由万向铰、移动副和转动副(R)组成。在机构的定、动平台上各建立一坐标系，定坐标系o的原点位于U副的中心，xo轴平行于a1a2，yo轴平行于a2a3，zo轴垂直于定平台向上。动坐标系p固连于动平台，其原点位于动平台的中心，初始位置时方位与定系重合。转动副固定于动平台，其轴线与约束分支U副的第2个转动轴线平行。机构下铰链点矩阵分布，上铰链点为梯形分布，其中梯形关于yp轴对称。

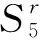
2 旋量牛顿-欧拉公式及坐标不变性

2.1 旋量速度、加速度描述

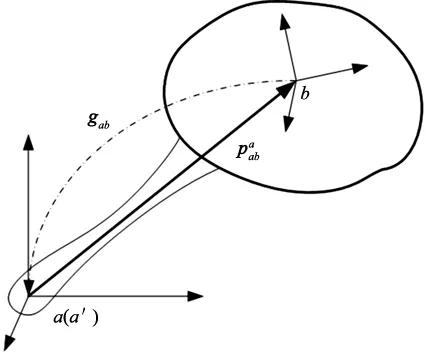
图2 单刚体的运动示意图

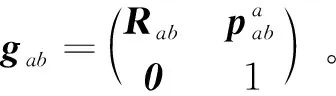
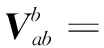
(1)

(2)

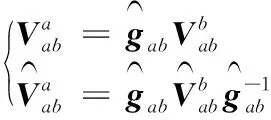
(3)

旋量加速度同样符合上述变换关系。

2.2 旋量形式的牛顿-欧拉公式

根据传统形式的牛顿-欧拉公式，刚体b的力、力矩平衡方程为:

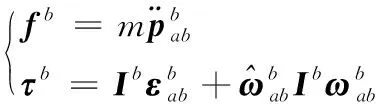
(4)

其中，m为刚体b的质量；fb为作用在刚体b上的三维力矢量在b系中的表示；τb为作用在刚体b上的三维力矩；Ib为刚体b的三维转动惯量在b系中的表示。结合式(2)，式(4)可以整理为：

(5)

结合旋量速度的伴随表示，式(5)可以表示为：

(6)

其中，Wb=(τb;fb)为作用于刚体的力旋量。Nb为刚体表示在b系中的6×6广义惯量矩阵。式(6)即为物体坐标系中旋量形式的牛顿-欧拉公式，给出了力旋量作用下刚体运动的全面描述。

2.3 牛顿-欧拉公式的坐标不变性

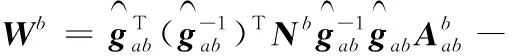
(7)

(8)

(9)

式(6)和式(9)在形式上保持了统一，说明旋量形式的牛顿-欧拉公式具有坐标不变性。

3 并联机构动力学模型及耦合指标

3.1 动力学Hessain矩阵

(10)

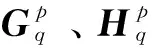
(11)

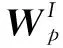
(12)

其中，Np为动平台的6×6惯量矩阵。将动平台的旋量加速度公式代入式(12)可得：

(13)

式(13)右边第2项可以表示为：

(14)

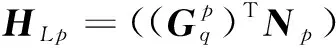
(15)

将式(14)和式(15)代入到式(13)中，整理可得：

(16)

同理，机构中第i个分支，第k个杆件的惯性力产生的主动关节驱动力可以表示为:

(17)

合并式(16)和式(17)可得机构包含动平台及分支的动力映射关系

(18)

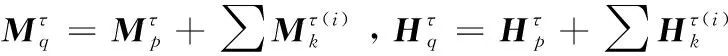
3.2 动力学模型

忽略摩擦，根据虚功原理，机构所有的力旋量处于平衡状态，则并联机构的动力学方程为:

τI+τG+τF+τA=0

(19)

其中，τG为机构的重力产生的广义驱动力；τF为作用在动平台的外力产生的广义驱动力；τA为机构的广义驱动力。并联机构动平台及所有杆件的重力产生的广义驱动力为:

(20)

并联机构动平台所受外力产生的广义驱动力可表示为:

(21)

将式(20)和式(21)代入到式(19)可得并联机构在关节空间表示中的动力学模型为:

(22)

3.3 动力学耦合指标

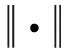
(23)

机构的动力耦合指标定义为:

(24)

ρA为机构位姿、动平台及分支惯量的函数，反映了机构的惯量与驱动力的传递密度。ρA值越大，机构的加速度能力越差。

机构在运动过程中，尤其是高速运动过程中，其向心力和科氏力往往不能忽略，机构的惯性力耦合指标定义为：

(25)

4 数值算例

4UPS/UPR并联机构初始位姿时坐标系o和坐标系p方位重合，初始高度H=0.38m。表1和表2给出了机构的结构参数，其中，bi0为上铰链点在p系中的坐标。

表1 4UPS/UPR并联机构铰链点坐标 /m

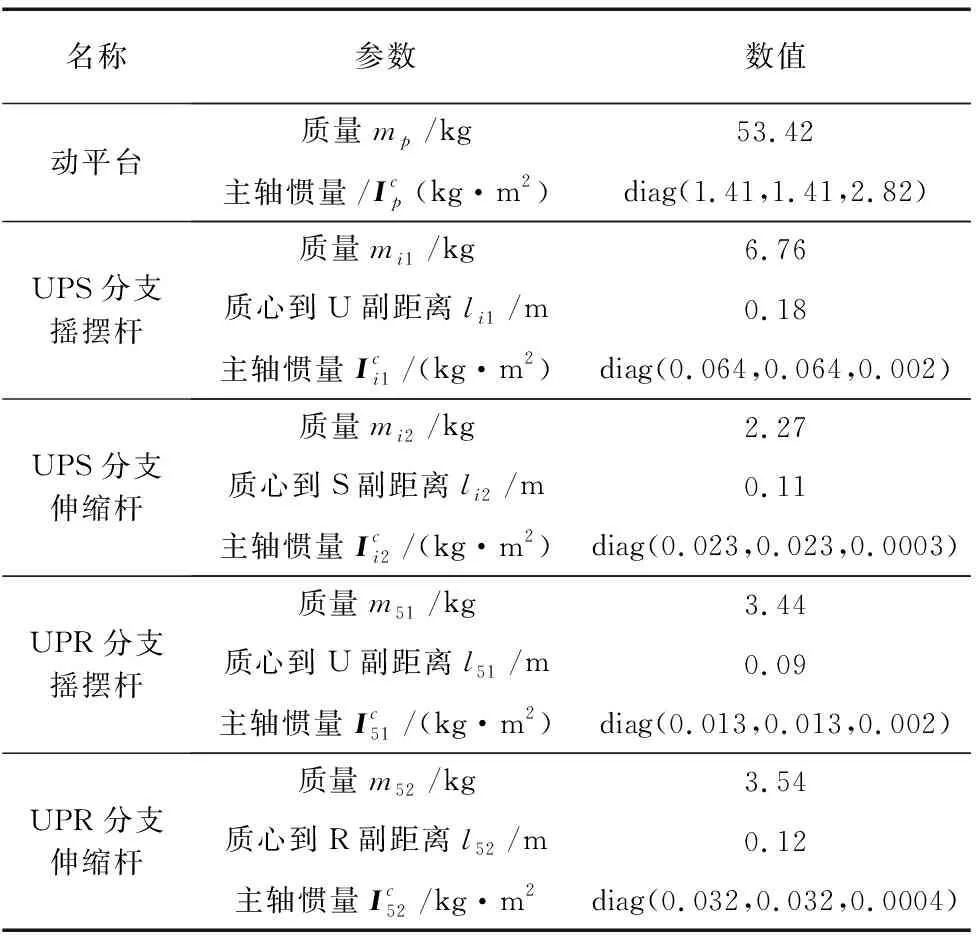
表2 4UPS/UPR并联机构结构参数

4.1 动力学模型验证

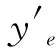
(26)

图3 4UPS/UPR机构分支示意图

忽略机构的重力及外力作用，采用上述动力学模型求解得到的机构主动关节驱动力如图4所示。图5为ADAMS软件仿真的结果。比较图4、图5可知，理论计算结果和软件仿真结果基本一致，验证了上述动力学模型的正确性。

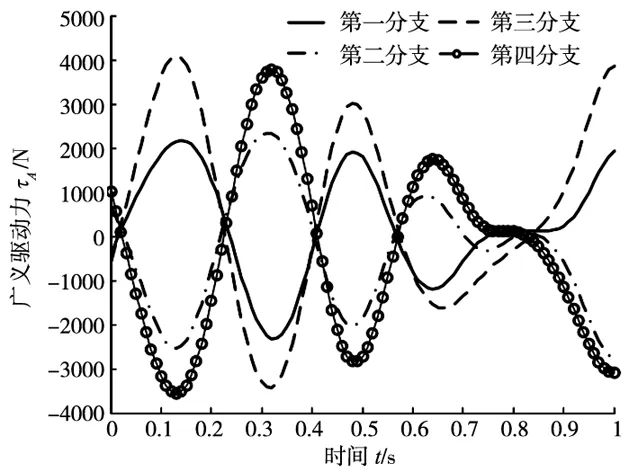
图4 上铰链点梯形布置时机构广义驱动力

4.2 铰链点参数对机构动力学影响

当上铰链点b30=b40=(0 -0.20 0)T，即上铰链点的布置由梯形退化为三角形，给定动平台式(26)的运动规律，通过动力学求解得到机构的广义驱动力如图6所示。通过比较图4、图6可以看出，对于相同的运动规律，上铰链点三角形布置时其广义关节驱动力明显减小。

图5 广义驱动力ADAMS仿真曲线

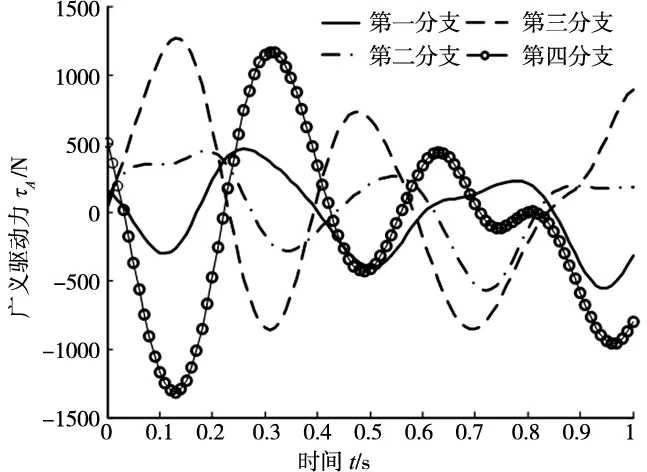
图6 上铰链点三角形布置时机构广义驱动力

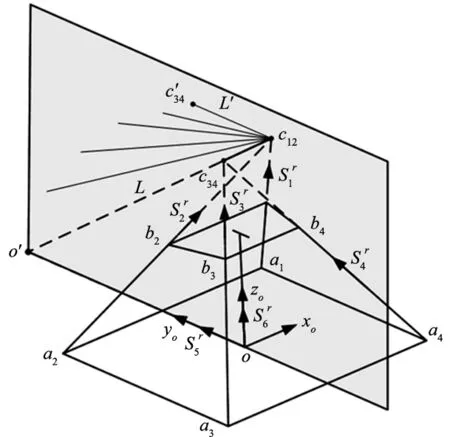
图7 初始位姿4UPS/UPR机构的约束特性

4.3 动力学耦合指标

4UPS/UPR机构上铰链点为三角形分布。图8给出了反映机构加速性能的动力耦合指标ρA，图9则给出了反映机构高速运动性能的惯性力耦合指标ρV。从图8、图9中可以看出，机构的动力学指标关于y轴对称，关于x轴不对称，这一现象符合机构上铰链点关于x轴不对称的布置形式。

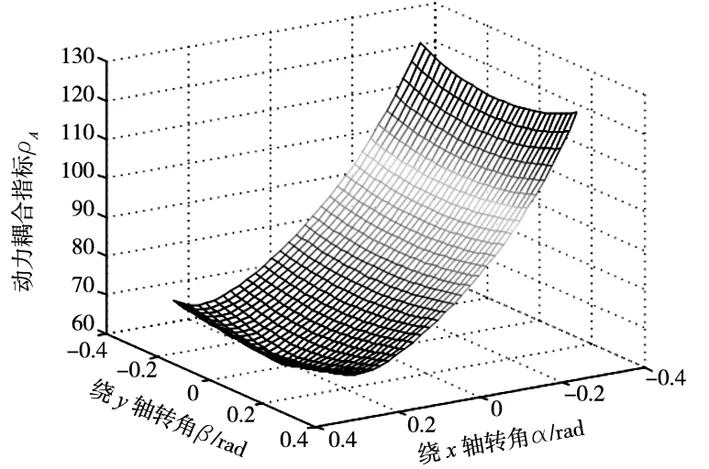
图8 4UPS/UPR机构的动力耦合指标

图9 4UPS/UPR机构的惯性力耦合指标

从图8、图9中可以看出，机构在α<0时的动力耦合指标ρA及惯性力耦合指标ρV明显大于α>0时。ρA、ρV的值越大，机构的惯性力映射到主动关节的驱动力越大。分别给定α=-0.3rad、α=0.3rad时，机构绕y轴的运动规律为β=0.20sin(15t)，机构广义驱动力的二范数如图10所示。从图10中可以看出，α=-0.3rad时广义驱动力的二范数明显大于α=0.3rad时，符合图8、图9机构动力学指标曲线的变化趋势。

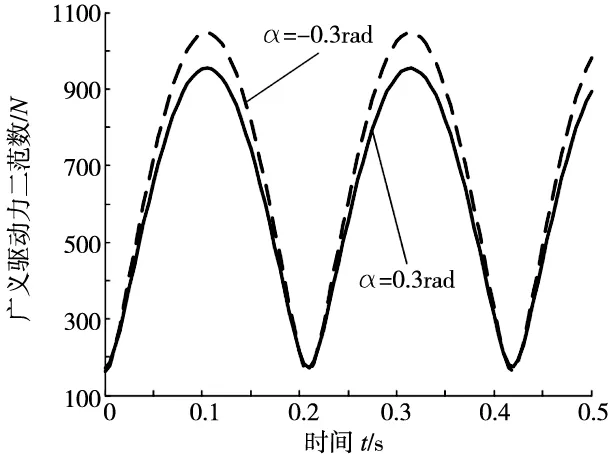
图10 4UPS/UPR机构广义驱动力的二范数

图11 公交线L在yozo面内的变化趋势

5 结论

(1)将传统形式的牛顿-欧拉公式表示成以运动旋量和力旋量为基本运算单元的旋量形式，并对其坐标不变性进行了证明。

(2)结合虚功原理及旋量形式的牛顿-欧拉公式，建立了4UPS/UPR并联机构的动力学模型，得到了动力学Hessian矩阵，并给出反映机构动力特性的动力学耦合指标。

(3)结合数值算例，分析了4UPS/UPR机构铰链点尺度参数对机构动力学特性的影响，并对其动力学耦合指标进行了分析。基于旋量的动力学建模方法形式简洁紧凑、易于编程，能够简化建模过程，为后续的动力学分析及控制奠定了基础。

[参考文献]

[1] 李永刚, 宋轶民, 冯志友, 等. 基于牛顿欧拉法的 3-RPS并联机构逆动力学分析[J]. 航空学报, 2007, 28(5): 1210-1214.

[2] 山显雷, 程刚. 考虑关节摩擦的3SPS+1PS并联机构显式动力学建模研究[J]. 机械工程学报, 2017, 53(1): 28-35.

[3] 张军, 谢志江. 基于Lagrange方程的3-PPR并联机构动力学分析与仿真[J]. 组合机床与自动化加工技术, 2016(8): 57-60.

[4] 薛帮灿, 郝丽娜, 杨辉. 3DOF-PAM并联机器人设计与动力学建模[J]. 组合机床与自动化加工技术, 2016(7): 52-55.

[5] 理查德·摩西, 李泽湘, 夏恩卡·萨思特里.机器人操作的数学导论[M]. 北京: 机械工业出版社, 1995.

[6] 郭菲, 李永泉, 宋肇经,等. 旋量键合图在并联机构动力学建模中的应用[J]. 机械工程学报, 2015, 51(23):12-20.

[7] Gallardo J, Rico J M, Frisoli A, et al. Dynamics of Parallel Manipulators by Means of Screw Theory[J]. Mechanism and machine theory, 2003, 38(11): 1113-1131.

[8] Sugimoto K. Matrix Representation of Kinematic and Dynamic Analysis of Mechanisms[C]//Proceedings of a Symposium Commemorating the Legacy, Work and Life of Sir RS Ball,2000: 1-14.

[9] Brand L. Vector and Tensor Analysis[M]. 6th ed. New York: John Wiley & Sons, 1957.

[10] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社，2006.

[11] 耿明超, 刘丽娟, 张灿果,等. 基于旋量代数的机器人运动学建模及应用[J]. 河北建筑工程学院学报, 2017, 35(2): 118-121.