自适应卡尔曼滤波的电离层TEC预测模型改进

王建敏，黄佳鹏，刘梓然，祝会忠，马天明

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.辽宁科技大学 土木工程学院，辽宁 鞍山 114000)

0 引言

由于电离层自身的不稳定性，对于穿过该层的全球卫星导航系统(global navigation satellite system，GNSS)的电波会产生折射、散射等物理现象。电离层总电子数(total electron content，TEC)是反映电离层状况的重要属性，电离层TEC的波动情况将会对人类生活产生极大的影响。近几年业界使用GNSS针对电离层TEC进行监测，通过探测电离层的异常情况作为研究地震发生的先验信息。因此，研究预报模型对电离层TEC的变化情况进行高精度预报，进而揭示随着电离层TEC急剧变化可能发生的物理现象及自然灾害，具有重要的科研及实用的意义[1-4]。文献[1]使用国际GNSS服务(International GNSS Service，IGS)组织公布的电离层TEC进行自回归滑动平均模型(auto regressive and moving average model，ARMA)的建模与预测，以电离层平静期和活跃期为研究对象，预报6 d的相对精度达到80 %以上[1]。文献[2]使用自回归模型(auto regressive model，AR)对电离层TEC进行预报，使用不同的原始数据分别向后预测2 d、3 d，通过比较模型的预报精度，证明AR模型针对电离层TEC具有很好的预报精度[2]。文献[3]利用AR模型与误差反向传播神经网络模型(back propagation，BP)等组合模型完成电离层TEC预报，得到组合模型较单一模型可得到更好的预报结果的结论[3]。文献[4]利用神经网络模型完成1 d的电离层TEC预报，表明训练好的神经网络模型能够充分反映出不同季节电离层TEC的变化。文献[5]利用小波神经网络完成电离层TEC短期预报，在南北高纬度地区得到较高精度。以上研究均是直接基于IGS公布的数据完成预报，对于预处理方式大多以差分方式使数据平稳化；但差分方式多是以简单数学模型完成，并不完全遵循数据的变化规律，只能完成数据平稳化处理。这类模型针对具有剧烈变化性的电离层TEC数据进行简单的预处理，没有考虑到原始数据可能有误差的存在；因此针对电离层TEC预报的预处理十分必要。

传统卡尔曼滤波在对电离层TEC数据进行处理过程中存在一定的缺陷，可能会导致滤波发散。本文采用方差补偿自适应卡尔曼滤波，用已有的电离层TEC数据对动态噪声方差矩阵进行同步估计，减弱滤波模型所造成的误差。神经网络具有良好的学习功能，可根据原始数据情况进行自我修正，小波分析理论可充分突出不同频率情况的变化趋势；小波神经网络兼具了二者的优点，可充分拟合变化剧烈的电离层TEC变化情况。将方差补偿自适应卡尔曼滤波作为数据预处理方式引入小波神经网络对电离层TEC进行预报，用以降低可能存在的噪声对预测模型及预测精度的影响。

1 模型基本原理

1.1 卡尔曼滤波

卡尔曼滤波能减少随机噪声对电离层TEC观测量的影响。它具有最小无偏差性，是当前应用最广的一种数据预处理方法。它处理数据不仅会去除突变的数据，而且会保持数据原有的变化趋势，这样有利于预报模型的建立。离散线性系统的卡尔曼滤波方程包括状态方程和观测方程[6]为

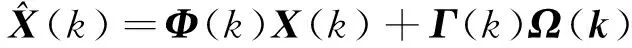
(1)

L(k)=B(k)X(k)+Δ(k)

(2)

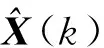
通过最小二乘原理可推得卡尔曼滤波方程为

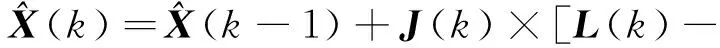
(3)

(4)

Dx(k)=(E-J(k)×B(k))×Dx(k-1)

(5)

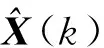
1.2 方差补偿自适应卡尔曼滤波

方差补偿自适应卡尔曼滤波就是在数据预处理过程中使用过去的电离层TEC数据对动态噪声方差矩阵进行实时估计，用以减少因滤波模型误差造成的噪声。其基本思路为：使用滤波值与真实值求得估计剩余，即

(6)

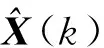
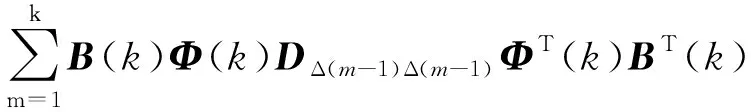
(7)

设式(7)中B(k)Φ(k)T=O(k,m)；而

(8)

因为E(VT(k)V(k))=trace[E(V(k)VT(k))]=traceDVV，则有

VT(k+i)V(k+i)=traceDVV+δk+i

(9)

式中δk+i为零均值随机变量。

令E(k)=VT(k)V(k)-trace[B(k)Φ(k)DX(k)ΦT(k)BT(k)]-traceDΔ(k)，又记

E=[E(k+1),……,E(k+N)]T，δ=[δk+i,……,δk+N]T。则有

E=OdiagDΔΔ+δ

(10)

式(10)是关于diagDΔΔ的矩阵，当N≥m时，有唯一解；则记diagDΔΔ估计为

(11)

通过式(11)完成卡尔曼滤波即式(5)的修正[8-9]。

使用方差补偿自适应卡尔曼滤波作为电离层TEC预处理方法。方差补偿自适应卡尔曼滤波是依据前一刻电离层TEC的状态量，结合观测方程去估计当前时刻TEC的滤波值，每一个电离层TEC数据都对应一个滤波后的滤波值，再以滤波值作为小波神经网络模型的输入值完成改进模型的建立。

1.3 小波神经网络

小波神经网络(wavelet neural network，WNN)是以神经网络为大体框架，将小波分析理论作为核心内容的神经网络。从结构形式上来看是将小波分解与BP神经网络相融合，用小波函数的平移因子充当隐层阈值作用，用小波函数代替隐层核心函数Sigmoid函数。由于小波神经网络需要参数较多，极大增强了样本数据与模型的关联度，使得模型比小波分解具有更优的逼近能力。不同网络层包括的神经元个数也各不相同。

小波神经网络核心部分表达式为

(12)

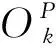
Morlet小波函数表达式为

(13)

(14)

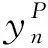
隐含层与输出层之间的权值调整公式为

(15)

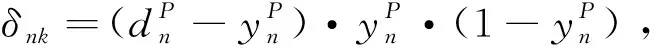
(16)

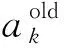
2 实验与结果分析

在利用预测模型对电离层进行预测时，对于电离层TEC可能存在的误差很少有人讨论；因此笔者使用方差补偿自适应卡尔曼滤波对电离层TEC进行预处理，用以降低原始电离层TEC可能存在的误差，进一步提高电离层TEC的预测水平。基于欧洲定轨中心(Center for Orbit Determination in Europe，CODE)下载的2016年电离层网格点TEC数据对该方法进行实验与分析，因自 2015 年起全球网格点数据以1 h为时间间隔，限于篇幅，选用2016年1月前10 d的数据。为验证该方法是否与数据的时间和纬度有关，取年积日为第1天至第10天全球不同经纬度的格网点数据作为实验数据，格网点的经纬度包括(87.5°N，125°E)、(67.5°N，125°E)、(45°N，125°E)、(22.5°N，125°E)、(0°，125°E)、(22.5°S，125°E)、(45°S，125°E)、(67.5°S，125°E)、(87.5°S，125°E)[15-16]。利用AKN模型、KN模型与AN模型完成对于对上述基础数据的预报，使用前10 d的TEC值分别预测后6 d的数据，比较不同情况下的预测精度。AKN模型使用方差补偿自适应卡尔曼滤波预处理，再利用小波神经网络完成预测；KN模型使用传统卡尔曼滤波预处理，再利用小波神经网络完成预测；AN模型直接使用小波神经网络完成预测。为验证模型在磁暴情况下的预测水平，使用2004年第302天至第311天作为原始数据，完成2004年第312 天至第316天的数据预测，选择格网点为(45°N，125°E)[17]。选用预测平均精度和残差值分布数据作为精度分析标准。

预测平均精度

(17)

式中：pi为不同预测模型i时刻的预测数据；qi为CODE公布的对应时刻实际TEC数据。

残差值V表达式为

V=pi-qi

(18)

图1为2016-01-10—2016-01-16不同纬度的3个预测模型的预测情况比较。图1中横坐标为预测历元，其中历元间隔为1 h；纵坐标表示TEC值，以总电子含量单位(total electron content units，TECU)的个数计，1个TECU等于1016个电子每平方米。

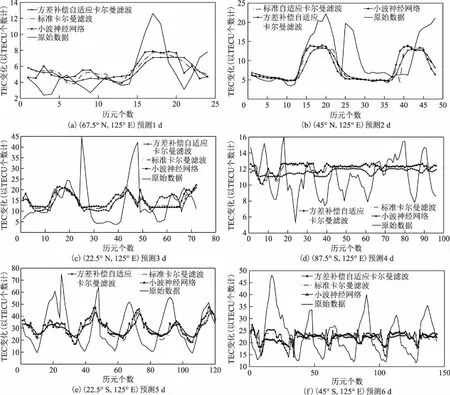
图1 不同天数的预测情况比较

由图1中可以看出：在不同纬度完成预测不同天数情况下，3个模型都有很高的拟合程度；利用方差补偿自适应卡尔曼滤波完成对于原始数据的预处理，相对另外2种模型具有更高的平均精度。

表1为3种不同模型在各个纬度下使用10 d数据完成预测的1～6 d的平均精度。

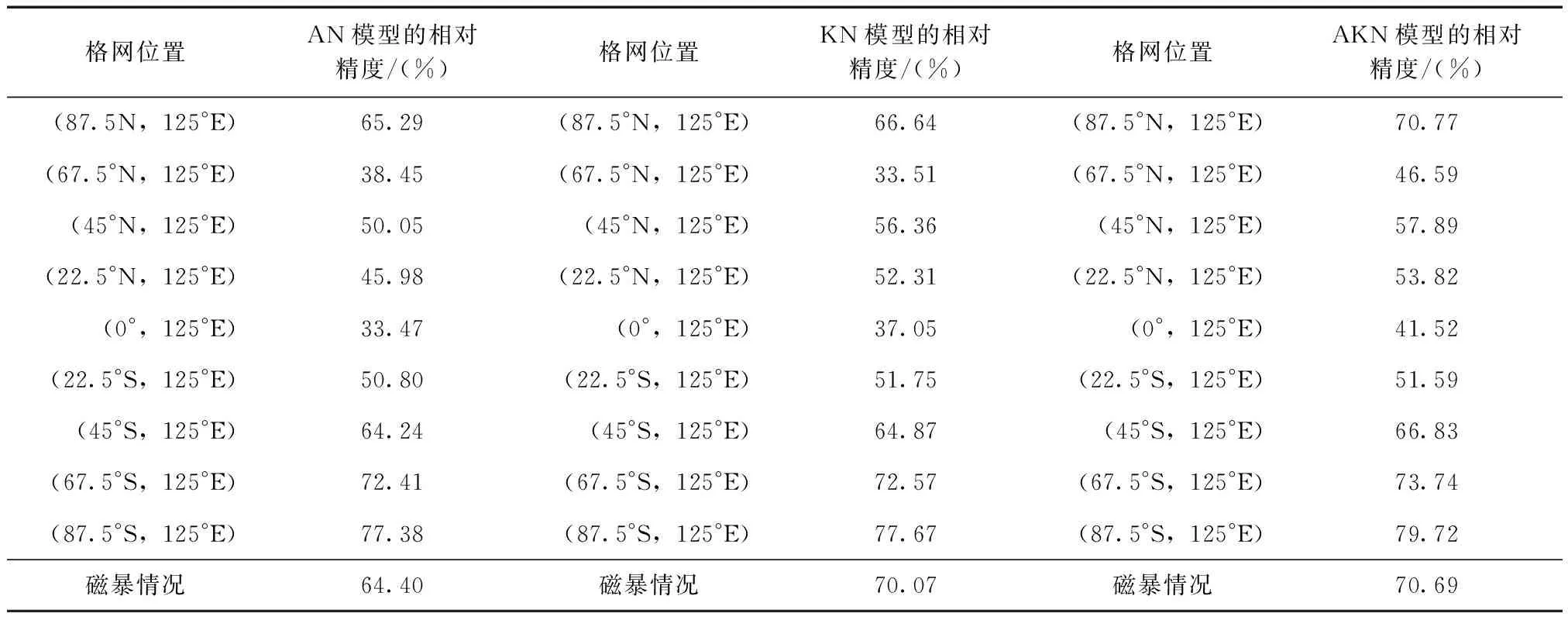
表1 不同纬度的相对精度统计

从表1中可以看出，在南半球AN模型、KN模型、AKN模型能够取得较好的预测精度，而且在(87.5°S，125°E)区域预测精度最高，在该区域经过方差补偿自适应卡尔曼滤波预处理的数据再利用模型进行预测会有更高的预测精度。由于是由小波神经网络完成预测，可能导致预测精度在某一区域较低，如(0°，125°E)区域，可能是由于该区域在这一时段不稳定造成的；但是经过卡尔曼滤波的预处理，提高了模型的总体预测精度：从表中可得出AKN模型预测精度相对KN模型和AN模型有不同程度的提高。从表中亦可看出纬度越高预测模型预测精度相应提高，(87.5°N，125°E)和(87.5°S，125°E)是各自半球预测精度最高的。高纬度地区是电离层异常活跃的地区，结合本次实验预测结果和原始数据曲线可以发现，在实验区间处2个高纬度区域的电离层TEC变化虽然不规律，但是电离层TEC变化范围相对其他纬度更小，可能是导致预测模型精度更高的原因。

图2为2004年磁暴现象预测结果，2004年CODE公布的数据历元为2 h，5 d共有60个TEC数据，图中第20个历元至第28个历元能明显看出与周围数据不同，通过比较3种模型拟合情况结合表1中数据可以看出，在磁暴预测情况下，AKN模型相对AN模型、KN模型有更好的预测效果。图3为不同模型不同纬度的平均预测精度。

表2为不同模型在不同纬度预测残差小于1个TECU的统计情况(预测1～6 d的平均值)。从表中可知：AN模型有16.64 %的残差值小于1个TECU；AKN模型有20.37 %的残差值小于1个TECU；在各个纬度AKN模型预测残差小于1个TECU所占的比重相对另外2个模型都有不同程度的提高。

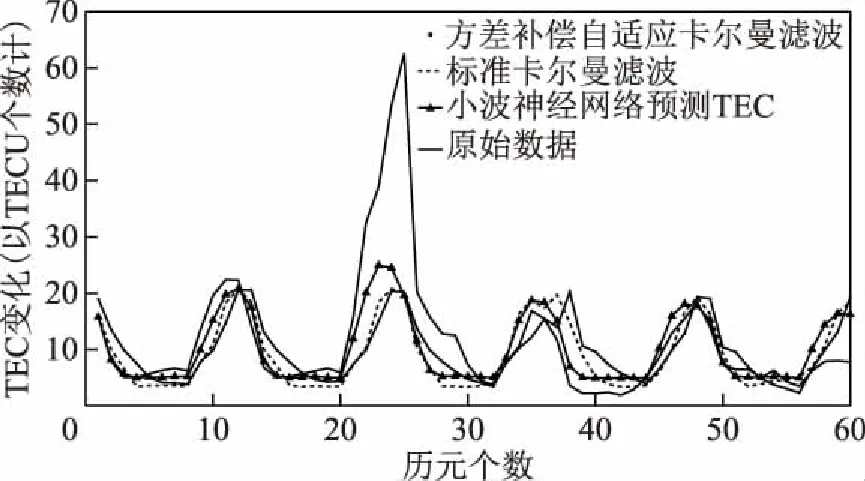
图2 磁暴现象预测5 d结果

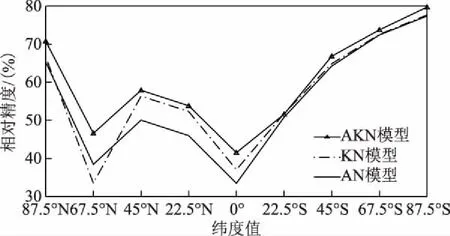
图3 不同纬度的相对精度统计图

结合表1、表2会发现：在各个纬度残差分布情况和预测的相对精度趋势不相同，这是由于预测精度的计算结果在很大程度上取决于基础数据的大小，相同或相近的预报残差，若基值不同，相对精度会有较大差异；各个纬度原始TEC数据有很大差异，如(67.5°N，125°E)的数量级是5个TECU，(0°，125°E)的数量级是50个TECU，所以即使残差较大，也可能具有略高的平均精度。综合2种精度评价标准来讲，使用方差补偿自适应卡尔曼滤波预处理可以提高模型的预测精度，是一种比较理想的提高预测精度的方式。

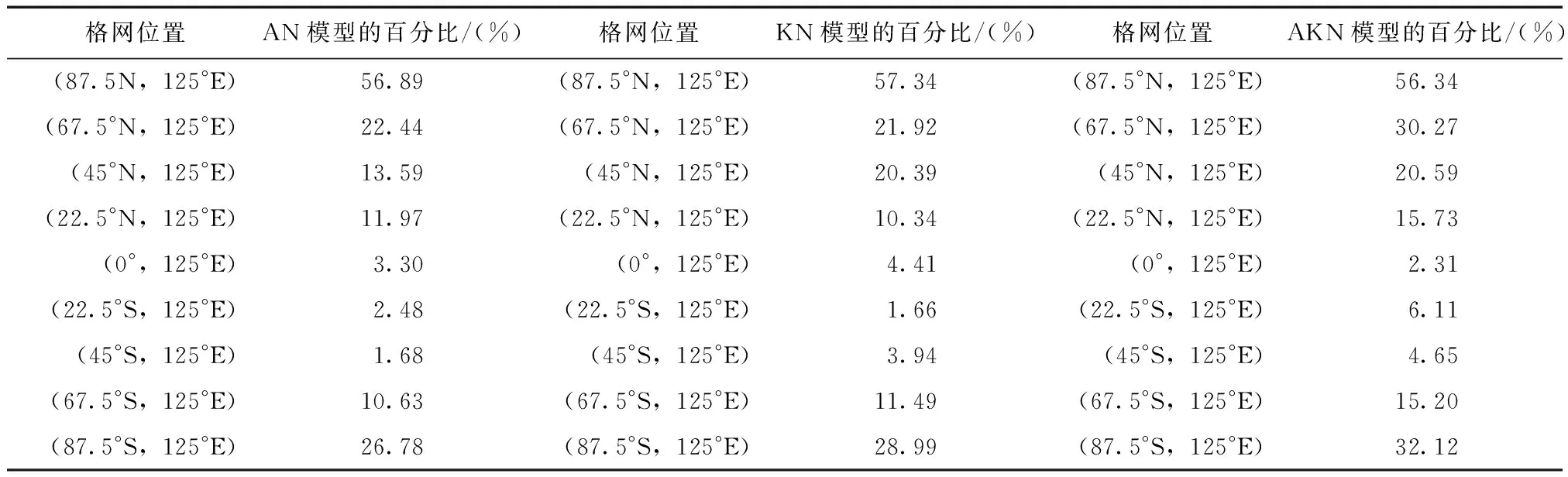
表2 不同模型预测残差小于1个TECU所占百分比

表3给出预测不同天数平均精度的统计结果。

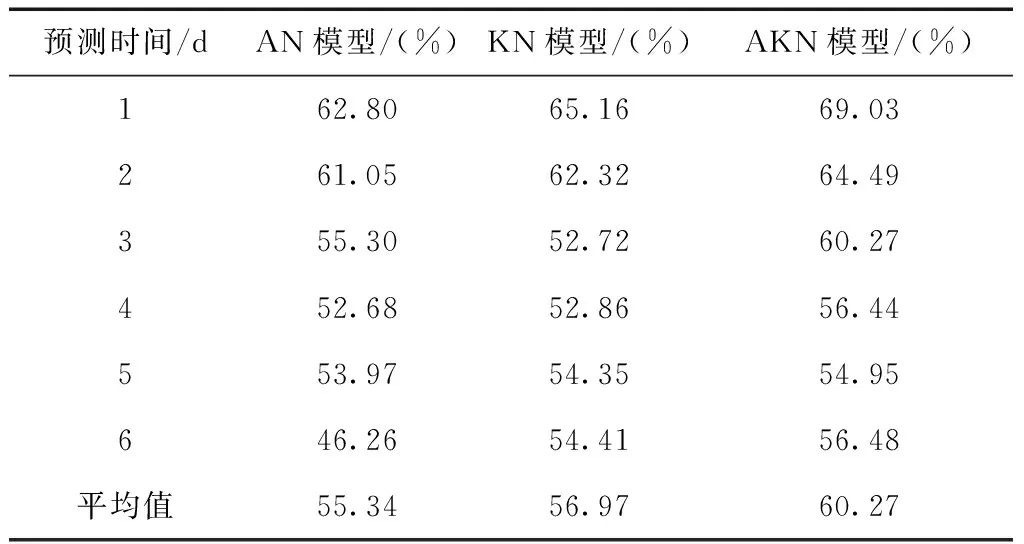
表3 预测不同天数的平均精度统计

图4为预测不同天数各模型平均精度的比较情况，由AKN模型变化趋势结合表3可知，预测不同天数情况下的AKN模型预测精度在54 %～69 %范围内，预测平均精度为60.27 %，预测平均精度相对直接使用原始数据进行预测提高4.93 %，且在预测6 d过程中保持逐步降低的总体趋势，超过4 d其相对精度将随时间明显降低。

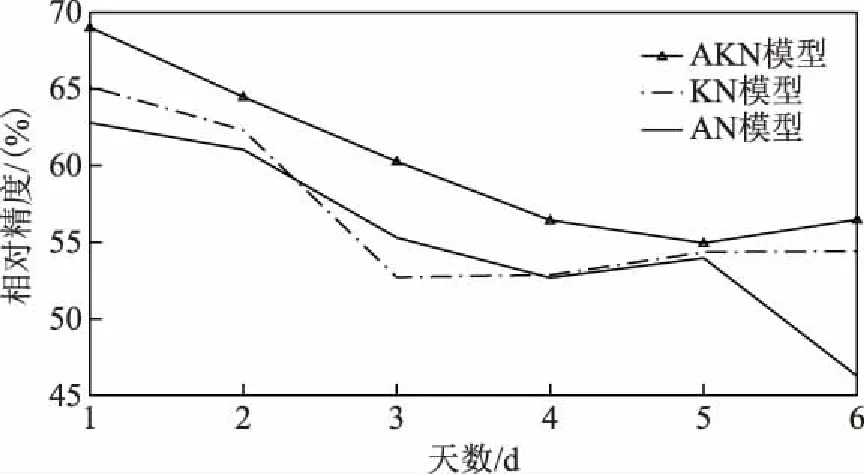
图4 不同天数各模型的相对精度比较

图5、表4为预测不同天数各模型残差小于1个TECU的统计情况，从中可知：根据AKN模型的变化过程，预报残差小于1个TECU的占20.37 %，相对直接使用原始数据建模提高3.73 %；且根据变化曲线来看，AKN模型随着预测天数的变化，残差也在略微改变，但是仍然优于另外2个模型。

图5 不同模型预测残差小于1个TECU预测天数统计

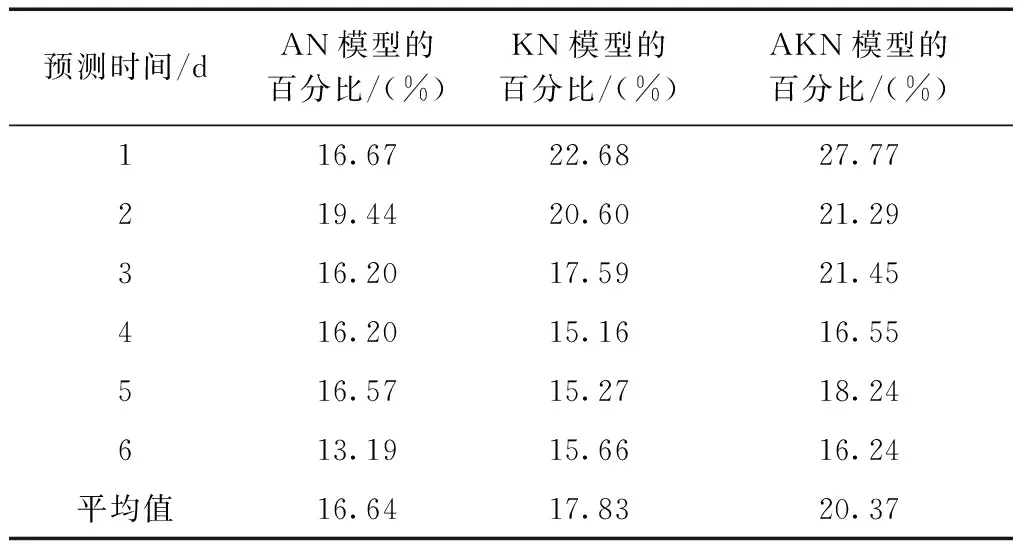
预测时间/dAN模型的百分比/(%)KN模型的百分比/(%)AKN模型的百分比/(%)116.6722.6827.77219.4420.6021.29316.2017.5921.45416.2015.1616.55516.5715.2718.24613.1915.6616.24平均值16.6417.8320.37

3 结束语

本文研究表明，使用方差补偿自适应卡尔曼滤波对电离层TEC进行预处理，再利用小波神经网络完成预测结果较为理想。无论是高纬度、中纬度，还是低纬度地区，经过自适应卡尔曼滤波预处理的电离层数据，再利用小波神经网络模型完成预测，能够在不同程度上提高预测精度，降低残差值的影响。使用该方法预测样本长度会对模型有很大影响，其大体规律为随时间增加，模型预测精度随之降低。

[1] 张小红，任晓东，吴风波，等.自回归移动平均模型的电离层总电子含量短期预报[J].测绘学报，2014，34(5)：118-124.

[2] 李秀海，郭达志.应用半参数AR模型的电离层TEC建模与预测[J].测绘科学，2011，36(2)：149-151.

[3] 王建敏，黄佳鹏，祝会忠，等.电离层总电子数预报方法研究[J].测绘科学，2016，41(12)：47-53.

[4] 李淑慧，彭军还，徐伟超，等.利用神经网络预报短期电离层TEC变化[J].测绘科学，2013，38(1)：8-12.

[5] 刘先冬，宋力杰，杨晓辉，等.基于小波神经网络的电离层TEC短期预报[J].海洋测绘，2010，30(5)：49-51.

[6] 郑崴，张贵宾.自适应卡尔曼滤波在航空重力异常解算的应用研究[J].地球物理学报，2016，59(4)：1275-1283.

[7] 茹国宝，冯鹏，邓勇.带状态切换自适应滤波算法及其在GPS/INS中的应用[J].武汉大学学报(工学版)，2015，48(4)：574-579.

[8] 李奕.自适应卡尔曼滤波在变形监测数据处理中的应用研究：以太原万达广场A2区基坑监测为例[D].成都：成都理工大学，2012：21-30.

[9] 王宇谱，吕志平，陈正生，等.一种新的钟差预处理方法及在WNN钟差长期预报中的应用[J].武汉大学学报(信息科学版)，2016，41(3)：373-379.

[10] 王宇谱，吕志平，陈正生，等.基于灰色模型与小波神经网络的卫星钟差预报方法[J].大地测量与地球动力学，2014，34(3)：155-159.

[11] 任强强，王跃钢，腾红磊，等.基于小波神经网络的盲区重力数据预测[J].大地测量与地球动力学，2016，36(4)：359-363.

[12] 葛玉辉，熊永良，陈志胜，等.基于小波神经网络的GPS可降水量预测研究[J].测绘科学，2015，40(9)：28-32.

[13] 陈标.短期电力负荷的小波神经网络预测[D].长沙：湖南大学，2012.

[14] 鲍亚东，刘长健，柴洪洲.小波分解改进电离层VTEC时间序列预报模型[J].大地测量与地球动力学，2015，35(5)：784-787.

[15] 李磊，张淑芳，胡青,等.ARMA模型在地震电离层TEC异常探测中的应用[J].大地测量与地球动力学，2015，35(1)：62-66.

[16] 时爽爽，黄劲松，冯建迪.基于IGS的白天和夜间电离层TEC变化特性分析[J].大地测量与地球动力学，2015，35(2)：293-297.

[17] 冯健，邓忠新，甄卫民，等.2004年11月强磁暴期间中国地区电离层TEC扰动特性分析[J].电波科学学报，2016，31(1)：157-165.