双馈风力发电机次同步扭振研究

赵雪娇， 彭志炜， 谭洪林， 毛雅茹， 李登瑞

(贵州大学 电气工程学院，贵州 贵阳 550025)

0 引言

随着全球污染的不断加剧和一次能源的无节制使用，各国学者都将目光投向了可再生能源，新能源发电也逐渐代替了火力发电成为了目前的关注焦点。风能在世界上很多地区储量都非常丰富，无污染，是最具潜能的可再生能源。比起其他新能源，风能发电的建设周期比较短，回报收益大，一般一个大型的风电场建设1～2年即可投入使用，是现有可再生能源里发展较为成熟的一种。近20年来，风能发电技术在一些地域辽阔的国家迅速发展。截止到2013年，我国新增装机容量16.09 GW，累计装机容量91.412 GW排名世界第一[1]。截止到2016年，累计装机容量高达168.69 GW[2]。2017年全球风能理事会(GWEC)最新发布的数据中显示，中国新增装机容量19.5 GW，占2017年全球新增风电机组容量的37%，累计装机容量高达188.19 GW。随着风电机组装机容量的不断增长，对风机并网时的安全稳定性要求逐渐提高，风电送入系统时可能发生的问题受到了大家的关注[3]。特别是在发生了一些大型事故之后，风电机组的SSO问题引起了国内研究人员的注意。

风电机组在采用电力电子设备接入电网时易与电网交换电气量，以致引发SSO现象[4]。除此之外，风电场在接入串补时也容易发生SSO现象。2009年，美国的一个双馈风力发电厂发生接地故障使系统接线方式改变后，装置检测到20 Hz的SSO频率，此次事故造成了大量风机脱网。2011年，河北沽源风力发电厂风电机组多次发生以DFIG为主的由串联补偿引起的次同步振荡，其频率在3～10 Hz之内[5]。发生SSO事故不仅会破坏风电机组，还会影响电网的正常运行，所以防止大型风电机SSO的发生尤为重要。如果没有完善的措施预防和抑制振荡问题，可能会导致发电机组被破坏甚至脱网，给国民经济造成重大损失。因此，预测、防止和抑制双馈风机SSO的发生对电力行业的发展起着关键性的作用。为了预防大型事故的发生，需要对可能存在的威胁进行深入研究。

SSTI是在某种瞬时扰动时产生的，会影响风力发电机轴系的旋转角度和速度，此时，就形成了扭转振荡[6]。大部分的风电系统扭振问题都是由风速等小扰动而引起的，也有部分是由严重的电网故障引起的大扰动扭振问题。文献[7]认为，若励磁控制器参数设置不匹配会引发SSO问题。文献[8]证明，在增加风机转速、输出功率或者串补率时，发生机网扭振的概率会更大。文献[9]认为，若风力发电机的电气参数设置不当，可能会影响双馈风力发电机的动态特性，从而发生次同步扭振。文献[10]认为，DFIG中发电机转子含有转速控制器会对系统的SSTI状态有一定影响。

为了研究DFIG发生的SSTI现象，本文通过小信号分析，在MATLAB/SIMULINK中搭建了基于三质量块传动链模型的双馈风力发电机经串补并入电网的参考模型，用于分析DFIG次同步扭振的形成原因。

1 DFIG数学模型

本文主要研究DFIG次同步扭振问题，由于次同步扭振是一种机电耦合振荡，所以在建模时，除了叶片模型、感应发电机模型、励磁变换器模型等动态模型外，还需要较为精确的轴系模型[11]，此模型对DFIG的次同步扭振问题研究具有一定的普适性。

1.1 风力机模型

风力机和其传动系统是双馈风机重要的组成部分，当风速低于额定风速时，处于速度控制区域，保持最优转速运行，风力机变桨距系统不参与系统功率的调整，此时桨距角保持在零度最大程度捕捉风能；当风速高于额定风速时，需要限制输出功率不能大于额定出力，故变桨距控制系统感知到风速的变化并动作于调整功率输出。变桨距系统执行的动态方程可表示为：

(1)

式中：β为桨距角；βref为桨距角参考值；Tβ为桨距角调节系统时间常数；KPβ、KIβ分别为桨距角PI控制环节的比例参数和积分参数；ωr为同步磁场旋转角速度；ωref为角速度参考值。

1.2 轴系模型

DFIG的传动部分由桨叶、低速轴、齿轮箱、高速轴、感应发电机转子等构成。DFIG传动系统的主要功能是将通过风力机被转化的机械能输出，经过轴系传递给感应发电机，成为感应发电机的输入机械功率。风力机的传动系统就是双馈风机的轴系，是机电能量转换的关键部分[12]。在研究DFIG的次同步扭振问题时，只把轴系看作刚体明显不满足研究精度要求，为了与实际结构更加接近，本文搭建如图1所示由叶片、齿轮箱和发电机转子组成的三质量块轴系模型。

图1 三质量块模型

通过小信号分析，得到基于三质量块的线性化方程:

(2)

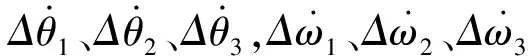
感应发电机的数学模型为：

Te=npLm(isqidr-idsiqr)

(3)

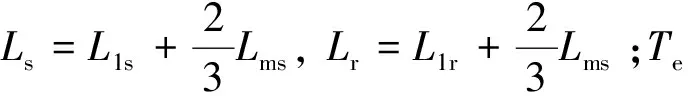
在稳定运行点处将上式线性化处理，则可得到感应发电机的小信号模型，此处不再作分析。

1.3 励磁变换器模型

转子侧变换器采用SVO方式，将定子电压空间矢量US与同步旋转坐标系的d轴重合忽略定、转子电阻，对RSC控制器引入状态变量x1、x2、x3、x4，则可得RSC小信号分析模型：

(4)

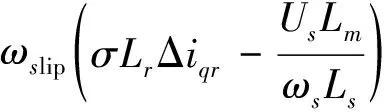
直流电容方程线性化后为：

(5)

引入三个状态变量x5、x6、x7，同理可得GSC小信号模型为：

(6)

式中：-Δiqg=iqgref-iqg；-ΔUdc=Udcref-Udc；Kp5和Ki5对应电压外环控制策略的比例系数与积分系数；Kp6和Ki6对应电流内环控制策略的比例系数与积分系数。

1.4 输电线路模型

感应发电机模型采用了d-q旋转坐标系，为了模型接口的对接，要使串联补偿线路坐标系与发电机坐标系保持一致，需要将静止的A-B-C三相对称坐标系变换为d-q旋转坐标系。d-q旋转坐标系下串联电容补偿线路在稳定运行点处的小信号模型为：

(7)

式中：ωb为b相角速度；uscq、uscd分别对应电容的端电压d、q轴分量；iRLq、iRLd分别为输电线路电流的d、q轴分量；uds、uqs分别是转子侧输出电压d、q轴分量；RL、XL分别为线路电阻和线路电抗；Xc是变压器等效电抗，XΣL为变压器电抗与线路电抗的总和。

联立方程(1)～(7)，形成全系统线性化方程，其中包括三质量块传动链模型、感应发电机、RSC、GSC及串补输电线路,形成DFIG经串补并网模型。

2 算例模态分析

在MATLAB/SIMULINK中搭建双馈风电机组经串补并网的仿真系统，对DFIG次同步扭振特性进行分析。DFIG单台电机额定容量为2 MW，三绕组变压器电压等级为 0.69/0.69/33 kV；并网机组有100台，线路中升压变压器电压等级为33/200 kV，故可模拟200 MW风电场运行情况。其风电并网等值系统接线图如图2所示。

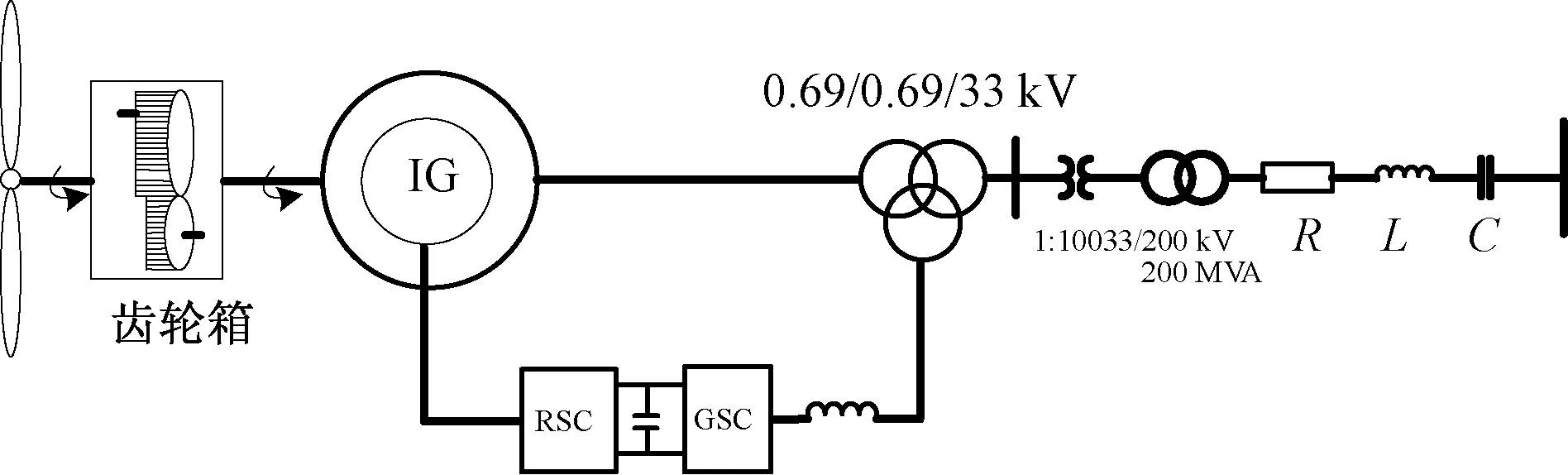
图2 双馈风机经串补并网模型

发电机详细参数如表1所示。

表1 单台2 MW双馈风电机组参数

对于风电场并网后的非线性系统在遇到小扰动时，其稳定性可将该非线性系统线性化，取稳定运行点的值作为参考依据[13]。根据Lyapunov小干扰判定原则，线性系统的稳定性可由22 阶系统的状态矩阵特征值表征，又由于求解出纯实数特征根、零模态与系统的振荡模态无关，本文不一一列出。表2给出了8个主要的振荡模态的的特征值。

由表2可知，求得的振荡模态1与2振荡频率为 1 384.5 Hz和70.61 Hz，超过工频50 Hz，为超同步模态；振荡模态8振荡频率为0.86 Hz低频振荡，本文不作相关分析。模态3～7为次同步振荡频率，由表2可知DFIG的次同步振荡频率都比较低，处于1.8～25 Hz之间。各次同步模态参与因子参与度分析如表3所示。

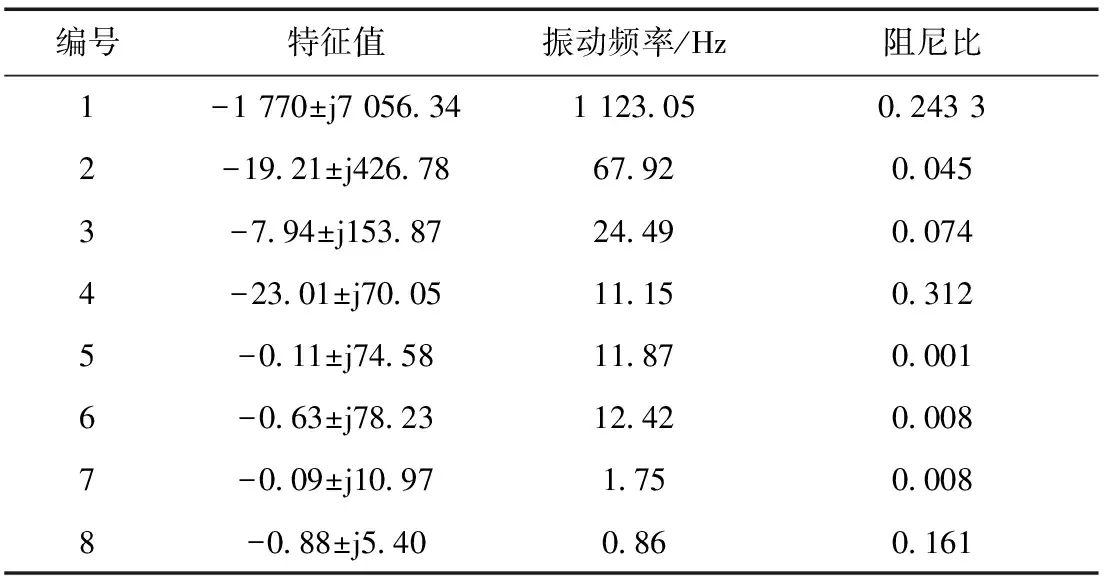
表2 系统的特征根

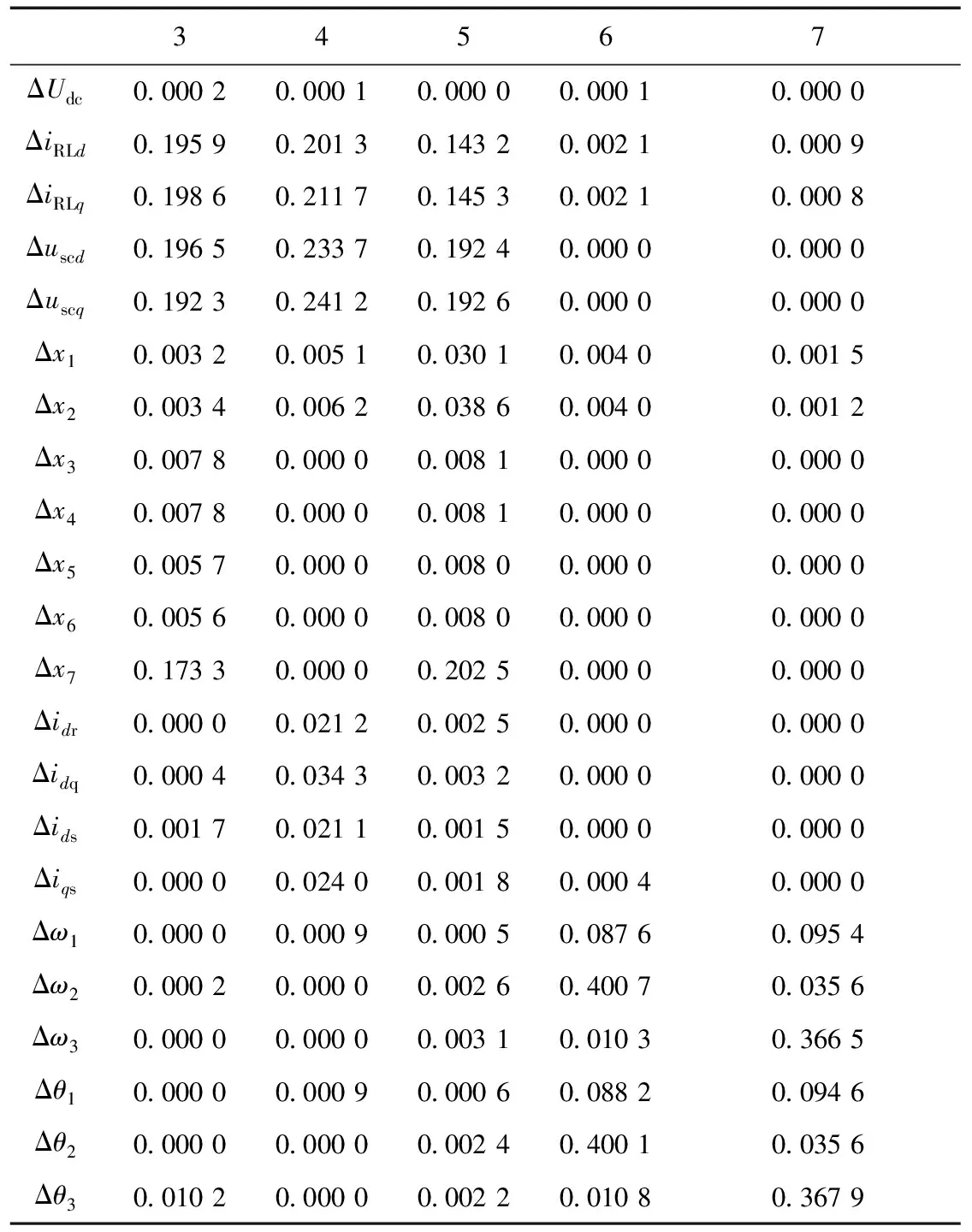
表3 各振荡模式参与因子

采用三质量块建模的系统有两个固有振荡模式，由表3对参与因子的分析可知，模态6和7主要与轴系相关，为固有振荡模式。其振荡频率分别为12.42 Hz与1.75 Hz，其中DFIG励磁系统控制器参数参与因子较低，证明双馈风机的次同步扭振与励磁系统关系不大。轴系状态变量、风力机转速与角频率的参与因子较高，模态6振荡频率为12.42 Hz，风力机叶片的旋转角和旋转角频率参与因子分别为0.088 2和0.087 6,模态7振荡频率为1.75 Hz, 风力机叶片的旋转角和旋转角频率参与因子分别为0.094 6和0.095 4。由此可知，次同步扭转振荡与风力机出力大小有关。

为了进一步验证风机出力大小对次同步扭振的影响，在2 s时加入串联补偿，将风速从8 m/s增至15 m/s，得到DFIG风速大小改变下的有功和无功波形。由于篇幅有限，本文只给出了风速为8 m/s、10 m/s、13 m/s、15 m/s时的波形，如图3所示。

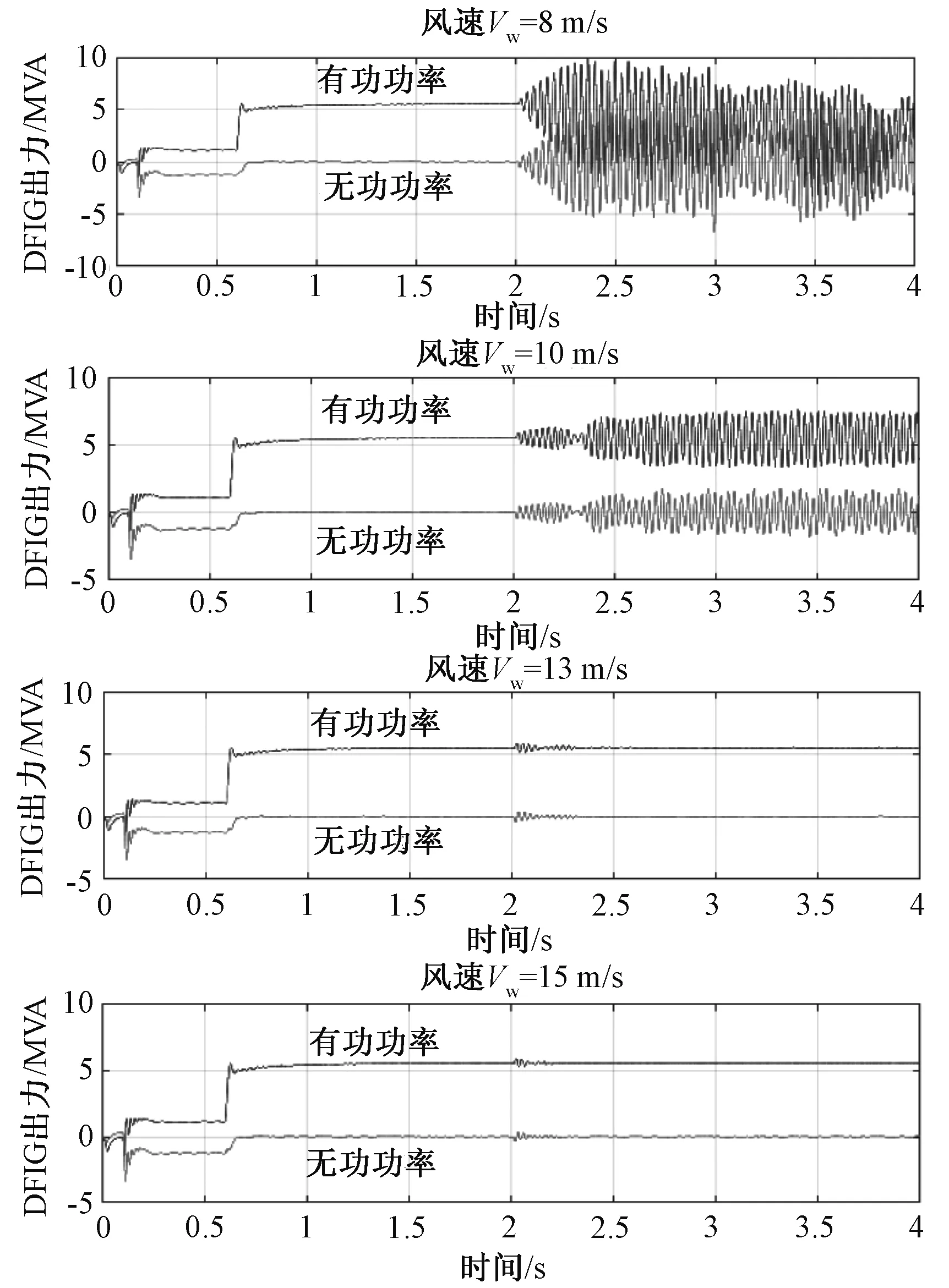
图3 不同风速下DFIG的有功和无功输出

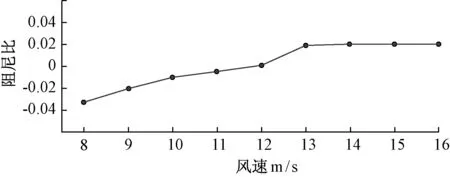
图4 阻尼比随风速的变化情况

由图3可知，随着风速的不断增加，系统的振荡频率逐渐下降，风速增至13 m/s后，系统作小幅振荡，且随着时间的推移，逐渐稳定。求得模态的阻尼比，风速与阻尼比的关系如图4所示。由图4可知，当风速不断增加时，系统的阻尼比也随之上升。当风速小于12 m/s时，系统呈现负阻尼，随着风速的减小，阻尼比也随之减小，此时系统功率振荡发散；当风速为12 m/s时，阻尼比近似为零；当风速大于12 m/s时，阻尼比为正，系统出现振荡幅度减小，且最后达到稳定；风速接近14 m/s时，系统的阻尼比大小变化微弱。

3 结语

(1)本文针对DFIG次同步扭振问题进行研究，通过小信号分析搭建200 MW风电机组经串补并入电网的仿真系统模型，得到固有振荡模式的参与因子。通过分析可知，在双馈风电机组中，次同步扭振与励磁系统PI参数关系不大。

(2)DFIG次同步扭振与轴系参数及风力机出力大小相关。随着风力机出力的增大，阻尼比随之增大，直到增大到某一定值不再变化。DFIG的有功无功随着风速的增大从大幅振荡逐渐到稳定收敛。证明在一定程度上增加风速，DFIG的次同步扭振可以得到一定的抑制。

参考文献：

[1]李俊峰,蔡丰波,高黎明，等.2013中国风电发展报告[M].北京:中国环境科学出版社, 2013．

[2]2016年全球风电装机统计[J].风能,2017(2):52-57.

[3]田旭,姜齐荣,谢小荣.电力系统次同步谐振抑制措施综述[J].电网技术,2010,34(12):74-79.

[4]董晓亮,谢小荣,杨煜,等.双馈风机串补输电系统次同步谐振影响因素及稳定区域分析[J].电网技术,2015,39(1):189-193.

[5]胡应宏,邓春,谢小荣,等.双馈风机-串补输电系统次同步谐振的附加阻尼控制[J].电网技术,2016,40(4):1169-1173.

[6]KUANYIN TIAN,PENG WANG,WENPING QIN,et al. Fatigue reliability analysis of wind turbines shafts caused by sub-synchronous oscillations during power system fault[C]//International Conference on Probabilistic Methods Applied to Power Systems, Beijing, China, 2016,1109(10):1-6.

[7]董晓亮,李江,侯金鸣.基于双馈风机转子侧变流器的次同步谐振抑制方法[J]电力系统自动化, 2016, 40(8):92-97.

[8]李先奇.变速风电机组风电场并网的系统电压稳定性研究[D].武汉：华中科技大学,2008.

[9]陈实,李宽,李兴源,等.大规模海上风电场经HVDC并网引发轴系扭振分析与抑制.四川大学学报:工程科学版.2015,41(6):144-149.

[10]娄宇成,解大,冯俊淇,等.基于三质量块模型的失速型风机小信号建模和模态分析[J].电力自动化设备,2015, 35 (8):124-130.

[11]宋少帅.双馈风力发电机次同步轴系扭振作用研究[D].保定：华北电力大学,2015.

[12]解大,冯俊淇,娄宇成,等.基于三质量块模型的双馈风机小信号建模和模态分析[J]中国电机工程学报,2013,33(S1): 21-29.

[13]李辉,陈耀君,赵斌,等.双馈风电场抑制系统次同步振荡分析及控制策略[J].中国电机工程学报,2015,35(7):1613-1620.