基于MapReduce的分布式贪心EM算法*

曹家庆, 吴观茂

(安徽理工大学 计算机科学与工程学院，安徽 淮南 232001)

0 引言

期望最大化算法(Expectation Maximization Algorithm，EM算法)是一种在概率模型中寻找参数最大似然估计或者最大后验估计的迭代算法，可以极大地降低求解最大似然估计的计算复杂度。然而传统EM算法作为数据挖掘中非常重要的聚类算法，在面对TB级别、PB级别等大规模数据集和高维数据集时，其缺陷显得越来越突出。因此如何对传统EM算法进行优化是机器学习算法的研究热点之一。现阶段对于EM算法优化的具体方向便是如何有效地处理如下两个问题：(1)初始模型成分数目需要人为设定；(2)收敛速度随着数据规模的增大而急剧减慢。

针对上述第一个问题，在传统EM算法的基础上使用贪心策略(贪心EM算法)，通过对仅含一个模型成分的高斯混合模型迭代增加新模型分量，直到满足某种终止条件为止。虽然该算法有效地提高了算法的准确度，但是上述第二个问题仍未得到有效解决。

为了解决上述问题，本文提出了一种分布式贪心EM算法。

1 相关工作

在EM算法和MapReduce的领域内,国内外已经有很多学者进行过深入的研究，因此本文基于EM算法和MapReduce的相关工作做进一步研究。

1.1 EM算法的相关工作

文献[1]中提出了一种基于MapReduce的EM算法，通过MapReduce的并行化处理解决了传统EM算法收敛速度随着数据规模变大而减慢的问题，但存在初始模型数需要预先设定的问题。文献[2]中通过使用牛顿法求解beta分布参数的算法，并提出一个合适的初值选择算法，使得EM算法能够有效地求解隐回归模型的参数，但是对所有的分布都采用beta分布作为自变量的假设会带来一定的偏差。文献[3]中提出了一种基于密度检测的EM算法，通过基于密度和距离的方法对初始值进行选择，降低传统EM算法的初始值选择对收敛效果的影响，但算法性能仍需提高。文献[4]中提出了一种快速、鲁棒的有限高斯混合模型聚类算法，通过对模型成分混合系数及样本所属成分的概率系数施加熵惩罚算子的方法，使算法在很少的迭代次数内收敛到确定值，但算法运行效率还需进一步提高。文献[5]中提出了一种快速、贪心的高斯混合模型EM算法，通过采用贪心的策略以及对隐含参数设置适当阈值的方法，使算法能快速收敛，并在很少的迭代次数内获取高斯混合模型的模型成分数，但是不能保证有噪声数据集的聚类效果。

1.2 MapReduce的相关工作

文献[6]中对Hadoop云平台下的聚类算法进行了研究。文献[7]中采用MapReduce编程模型，对特征选择算法进行了研究。文献[8]中提出了基于MapReduce模型的高效频繁项集挖掘算法，利用MapReduce框架对Apriori算法进行了改进，提高了Apriori算法运行速度。文献[9]中提出了一种基于MapReduce的Bagging决策树算法，运用MapReduce框架对决策树算法进行了并行化处理，提高了决策树算法对大数据集的分析能力。文献[10]中提出了一种基于MapReduce的文本聚类算法，运用MapReduce分布式框架对K-means算法进行了改进。文献[11]中对MapReduce近年来在文本处理各个方面的应用进行分类总结和处理，并对MapRedcue的系统和性能方面的研究做了一些介绍。文献[12]中总结了近年来基于MapReduce编程模型的大数据处理平台与算法的研究进展。文献[13]中基于MapReduce计算框架，对传统蚁群算法进行了改进，使得算法能够快速有效地处理大规模数据集。

2 分布式贪心EM算法

2.1 贪心EM算法

贪心EM算法的关键是通过全局搜索将原始数据集初始化为一个仅含有一个模型分量的高斯混合模型，然后通过局部搜索逐渐增加新的模型分量到原有的高斯混合模型中，不断更新混合模型分量的参数使得似然度最大。算法过程如下：

假设样本集X={x1,x2,x3,…,xm}，并服从高斯混合分布，则高斯混合分布的概率密度函数fk(x)[14]为：

(1)

其中，xi是p维向量，Φj(xi;θj)是第j个高斯模型分量的概率密度，θj是它的参数，wj是第j个分量的混合系数，表示第j个高斯模型分量包含的样本所占样本总数的比例,k是高斯混合模型的模型成分数[15]。θj=(μj,Σj)，μj为高斯模型分量均值，Σj为高斯模型分量协方差矩阵。其中高斯分量概率密度Φj(xi;θj)表达式为：

(2)

此时将某一新分量δ(x;θ)加入一个已有k个分量的混合密度函数fk(x)，则生成的新的高斯混合模型密度函数如下式所示:

fk+1(x)=(1-α)fk(x)+αδ(x;θ)

(3)

其中，α是新增模型分量的混合系数，0<α<1。则新生成的对数似然函数为：

(4)

已知新的高斯混合模型包括混合模型分量和新增分量，而混合模型fk(x)已被设置为不变，所以贪心EM算法的核心就是优化新增模型分量的混合系数α以及新增分量的参数，使新生成对数似然函数Lk+1最大化。所以，首先通过全局搜索找到一组新增分量的初始参数μ0、Σ0和α0。在α0处展开Lk+1的二阶泰勒公式并且最大化关于α的二次函数得到似然函数的一个近似:

(5)

(6)

则Lk+1在α0=0.5附近的对数似然局部最优可以写成：

(7)

(8)

在求出新增模型分量估计值之后，通过传统EM算法可得:

(9)

(10)

通过公式迭代获取新增模型参数最优解{αk+1,μk+1,Σk+1}，从而获取新的高斯混合模型的对数似然函数值Lk+1。

2.2 分布式贪心EM算法

依据MapReduce的框架结构，在设计分布式贪心EM算法时，首要的考虑便是定义Map函数和Reduce函数。算法过程如下：

(1)Mapper阶段

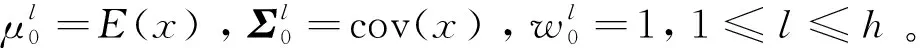
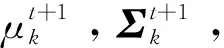
(2)Reducer阶段

步骤三：将所有节点得到的键值对进行整合，将高斯混合模型密度函数进行求和，然后再取对数，得到整合后的对数似然函数为：

(11)

步骤五:判断满足收敛条件的Fk是否满足Fk+1≤Fk，如不满足则重新进行步骤一，如果满足则结束算法，输出理想模型成分数k。

具体算法流程如下所示：

算法：分布式贪心EM算法

输入：样本集X={x1,x2,x3,…,xm}

输出：高斯混合模型理想模型成分数k

1 将数据集平均分配到h个节点中

2 While(true)

3 对于每个节点：

4 初始化节点，设置迭代次数ε=1

9 ifλ<10-6，则收敛结束

10 else跳转到步骤4，ε+1

11 end if

12 ifFk+1≤Fk，输出理想模型成分数为k，break

13 else跳转到步骤2。

14 end if

15 end while

本算法主要是在Map(映射)、Reduce(归化)、判断的过程中得到最优的最大似然Fk，从而得到理想模型成分值k。

上述算法中，步骤1～7为Mapper阶段，首先对每个节点初始化高斯混合模型参数，然后通过更新参数得到最新的高斯混合模型密度函数，最后将数据映射处理并生成相应的键值对，并作为Reducer阶段的输入。步骤8～11为Reducer阶段，此阶段是将Mapper阶段传递过来的键值对进行整合得到Fk，再利用判断因子λ判断是否满足收敛条件，当λ<10-6时，Fk达到收敛值，迭代结束。步骤12～15，因为在对原高斯混合模型添加新模型分量的过程中，数据集的对数似然函数值呈逐渐增长的趋势，所以当高斯混合模型的对数似然函数取得最大值，即当Fk+1≤Fk时，Fk为收敛值，即为最优解，则算法循环结束，k即为理想模型成分数。

算法复杂度分析如下：

3 实验结果与分析

3.1 实验环境

整个实验是在Hadoop平台下进行的，所用的版本为Hadoop2.6.5。每台主机系统使用的是Unbuntu14.04版本。建立的集群由1个主节点、4个从节点组成。所有节点的硬件设备为联想主机，其中使用了主频为3.3 GHz的Intel四核处理器，内存为2 GB。

3.2 实验数据

实验数据来自UCI机器学习和知识发现研究中使用的大型数据集KDD数据库存储库。其中第一组数据大小为0.6 GB，包含200个数据，模型成分数为9；第二组数据大小为1.4 GB，包含500个数据，模型成分数为9；第三组数据大小为2.0 GB，包含1 000个数据，模型成分数为15；第四组数据大小为3.2 GB，包含1 500个数据，模型成分数为15。

3.3 实验结果及分析

3.3.1运行时间

将本文算法与传统EM算法、贪心EM算法在求解高斯混合模型理想成分数的时间上作比较。固定节点个数为8个，分别使用本文算法、传统EM算法、贪心算法对4组实验试验数据求解高斯混合模型的成分数，并进行时间对比，实验结果如图1所示。

图1 算法运行时间比较图

三种算法下对于第一组和第二组实验输出模型成分数都为9，第三组和第四组实验输出模型成分数都为15，输出结果正确。由图1可以看出，对于这4组实验数据，本文算法相对于传统EM算法以及贪心EM算法在处理数据集时运行时间大幅减少，当数据规模更大时，速度优势更为明显，同时可以看出，随着数据集的变大，本文算法的运行时间基本呈线性增长，具有较好的数据可扩展性。

3.3.2系统的可扩展性

实验二通过改变节点个数，设置节点数分别为2，4，6，8，观察本文算法下求解4组数据的模型成分数的时间变化，实验结果如图2所示。

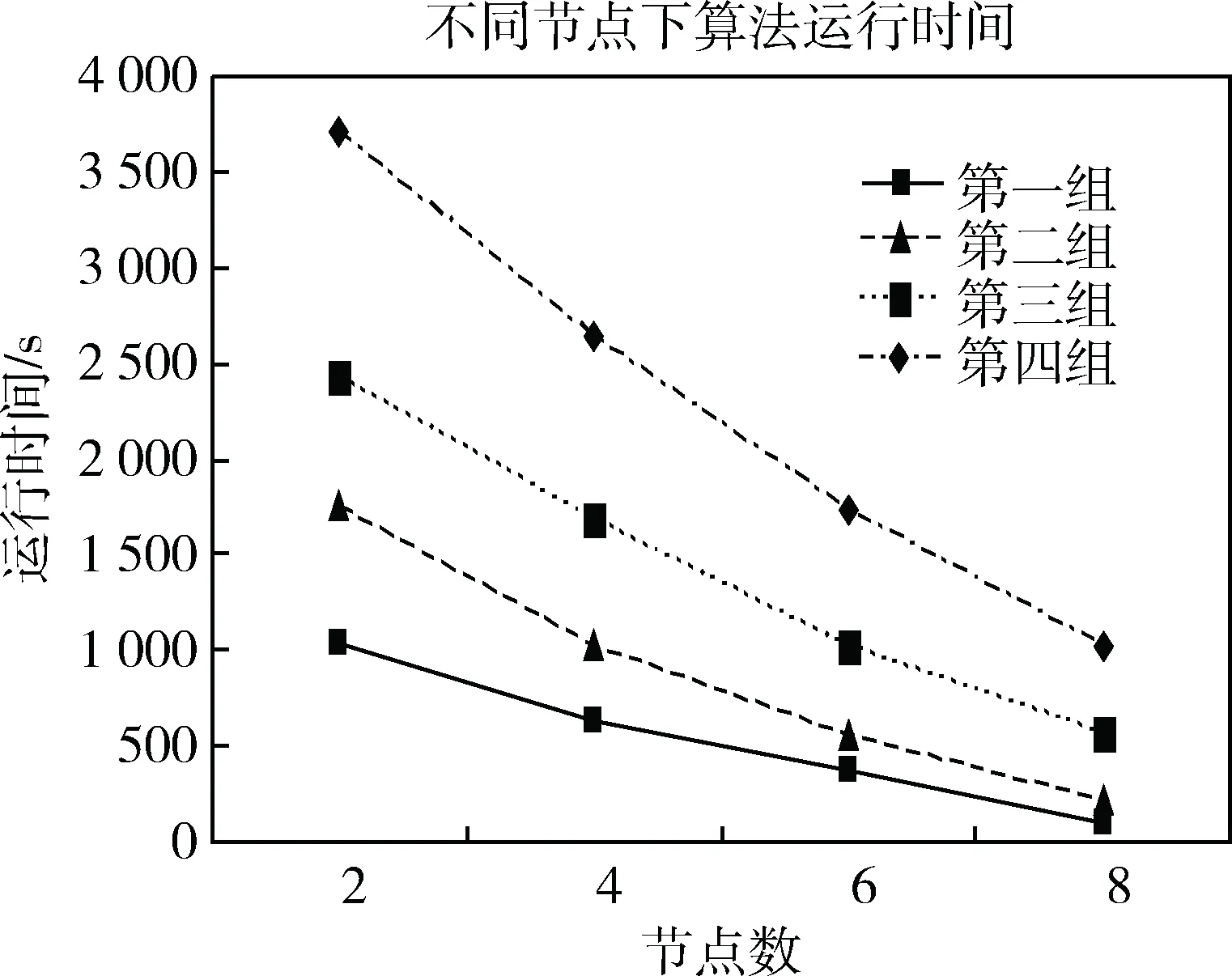
图2 不同节点下算法运行时间

由图2可以看出，随着节点数的增加，本文算法运行时间逐渐减少，因此可以通过增加计算节点的个数来增加本算法运行速度。同时在数据集较小的时候，随着节点数的增加，算法运行时间减少的幅度非常小，这是由于在小规模数据集下算法迭代计算的时间很小，时间大部分都花费在节点与节点之间的通信上。

4 结论

本文在贪心EM算法的基础上，提出了一种基于MapReduce分布式框架的贪心EM算法，该算法在保证了无需预先指定初始模型成分数目并能准确得到模型成分数的前提下，极大地提高了处理大数据集时的收敛速度。实验结果与分析表明，本文算法较之传统EM算法和贪心EM算法在处理大规模数据上有明显的加速效果，并且随着节点数的增加可以进一步提高收敛速度，并且具有很好的扩展性。实验仅对求解高斯混合模型的模型成分数的时间进行了对比，并未对聚类的准确度进行实验，因此后续研究者可以就高斯混合模型聚类的准确度作进一步研究。

[1] 胡爱娜. 基于MapReduce的分布式EM算法的研究与应用[J]. 科技通报, 2013(6):68-70.

[2] 韩忠明, 吕涛, 张慧,等. 带隐变量的回归模型EM算法[J]. 计算机科学, 2014, 41(2):136-140.

[3] 戴月明, 张朋, 吴定会. 基于密度检测的EM算法[J]. 计算机应用研究, 2016, 33(9):2697-2700.

[4] 胡庆辉, 丁立新, 陆玉靖,等. 一种快速、鲁棒的有限高斯混合模型聚类算法[J]. 计算机科学, 2013, 40(8):191-195.

[5] 邢长征, 苑聪. 一种快速、贪心的高斯混合模型EM算法研究[J]. 计算机工程与应用, 2015, 51(20):111-115.

[6] 谭跃生, 杨宝光, 王静宇,等. Hadoop云平台下的聚类算法研究[J]. 计算机工程与设计, 2014, 35(5):1683-1687.

[7] 陆江, 李云. 基于MapReduce的特征选择并行化研究[J]. 计算机科学, 2015, 42(8):44-47.

[8] 朱坤, 黄瑞章, 张娜娜. 一种基于MapReduce模型的高效频繁项集挖掘算法[J]. 计算机科学, 2017, 44(7):31-37.

[9] 张元鸣, 陈苗, 陆佳炜,等. 基于MapReduce的Bagging决策树优化算法[J]. 计算机工程与科学, 2017, 39(5):841-848.

[10] 李钊, 李晓, 王春梅,等. 一种基于MapReduce的文本聚类方法研究[J]. 计算机科学, 2016, 43(1):246-250.

[11] 李锐, 王斌. 文本处理中的MapReduce技术[J]. 中文信息学报, 2012, 26(4):9-20.

[12] 宋杰, 孙宗哲, 毛克明,等. MapReduce大数据处理平台与算法研究进展[J]. 软件学报, 2017, 28(3):514-543.

[13] 凌海峰, 刘超超. 基于MapReduce框架的并行蚁群优化聚类算法[J]. 计算机工程, 2015, 41(8):168-173.

[14] 马江洪，葛咏，图像线状模式的有限混合模型及其EM算法[J].计算机学报,2007,30(2):288-296.

[15] 李斌，钟润添，王先基，等. 一种基于递增估计GMM的连续优化算法[J].计算机学报，2007，30(6):979-985.