巧妙消元，雨扫梨花

（湖南省常德市石门县第三中学 湖南常德 415300）

二元一次方程组的解法是在“消元”的思想下进行的.对于一些特别的二元一次方程组，它的解法也有些特别，这些解法会使问题的解决变得简单，过程充满乐趣，解法富有新意，在解题过程中，能给人以启迪，使思维得到升华.现举例阐述如下：

一、参数换元，简化运算

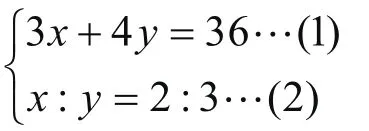
思路点拨：由方程（2）可知3∶2∶=yx，设x＝2k，y＝3k，则可用一个参数k替换两个变量x与y，从而达到简化运算的目的。

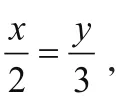
于是x＝2k，y＝3k，把它们代入（1）得

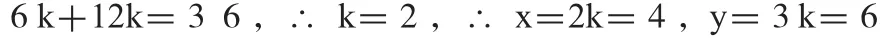
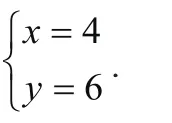
二、消去常数，另壁蹊径

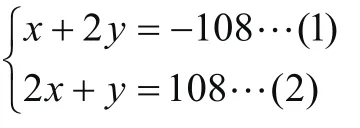
思路点拨：容易观察方程组中的两个常数互为相反数，不妨采取消去常数的方法一试.

解：（1）＋（2）得：3x＋3y＝0

∴ x＋y＝0……（3），将（2）－（3）得x＝108，

把x＝108代入（3）得y＝－108，

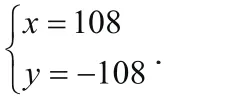
三、整体代入，总揽全局

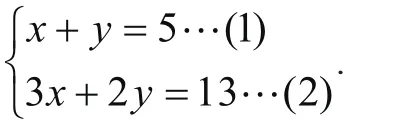
思路点拨：先将方程（2）变形为 3 (x+y)-y=13或x+2(x+y)=1 3，再把 x + y看成一个整体代入变形后的方程。

解：将方程（2）变形为)3(1 3)(2…=++yxx，

把 5=+yx 代入（3）得： 3=x ，

再把 3=x 代入（1）得： 2=y ，

四、整体加减，减少系数

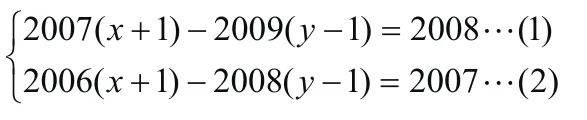
思路点拨：此题若用普通的代入、加减消元法，则计算繁琐，任务量大，观察方程组中系数特点，不难得到两个方程中未知数前的系数相差为1，可把方程（1）、（2）视为一个整体进行加减.

解：（1）－（2）得： (x+1)-(y -1)=1……（3），

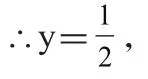
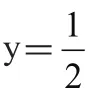
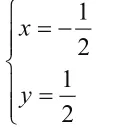
五、重复加减，快捷求解

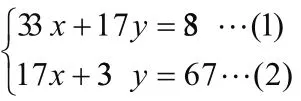
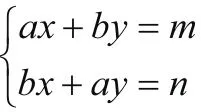
可以直接将两个方程相加减，反复两次，可巧妙地迅速求解.

解：（1）＋（2）得：)3(3…=+yx

（1）－（2）得：)4(1…=-yx；

（3）＋（4）得： ,2=x （3）－（4）得： 1=y

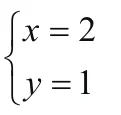
利用上述方法求解二元一次方程组时，犹如雨扫梨花一样，显得干净利落，非常有效。