层流边界层的直观模型

孙泽辉



层流边界层的直观模型

孙泽辉

（安徽大学 电气工程与自动化学院，安徽 合肥 230601）

在流体力学中，边界层的概念十分重要。首先用近似方法给出无限长边界处速度扰动在半空间流体中的一维传播定性规律，在此基础上通过引入层流边界层的直观模型，仅通过运动学角度的几何分析，给出了层流边界层的形成及厚度演化过程的直观描述，并总结了平板层流边界层形成的物理及几何条件。

边界层；直观模型；运动学分析

在流体力学中，边界层不仅是重要的理论概念，其在工程应用中也十分重要[1]。只有深刻理解边界层概念，才能理解关于边界层的各种工程计算[2-5]，并能应用边界层理论进行工程设计[6-7]。在阐述边界层的概念和尺度特征时，通常教科书的做法是从Navier－Stokes方程出发，通过对方程中各项的无量纲化和量阶分析，建立简化的边界层方程，然后进行偏微分方程的求解。然而，在进行繁琐的方程简化和求解的同时，却缺乏对边界层形成和厚度演化过程的直观描述。

本文首先给出无限长平板板面处速度扰动在半空间流体中的一维传播定性规律，在此基础上建立平板层流边界层的直观模型，通过对任一流体面运动的讨论，从运动学角度描述了平板层流边界层形成的机制和厚度演化的定性规律，并总结了产生边界层的物理及几何条件。

1 无限长平板板面处速度扰动在半空间流体中的一维传播规律

一块水平放置的无限大平板，上半空间充满粘性流体。流体和平板一起，以速度0在平板自身平面内沿轴方向运动，如图1所示。在＝0时刻，平板突然静止不动。由于粘性，板面处的流体流动会因平板的突然停止而受到阻滞，从而引起流体速度场的扰动，该速度场扰动将沿着方向传播。下面分析流体速度场扰动传播距离随时间变化的定性规律。

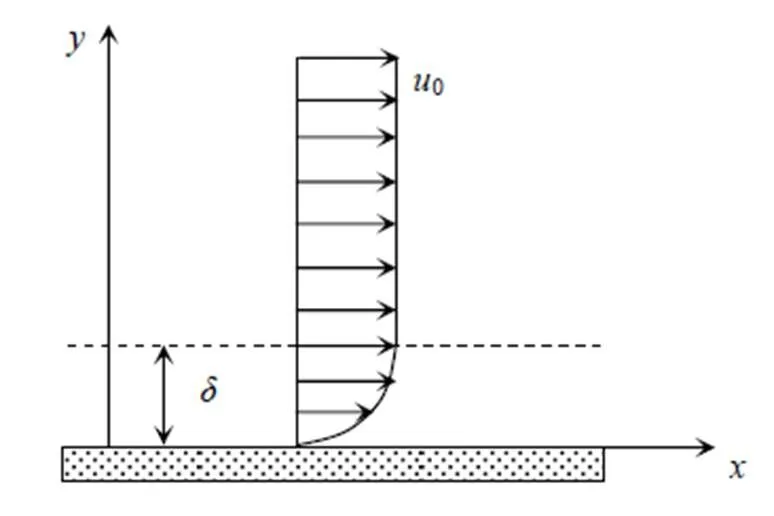
图1 无限长平板边界区域流速分布示意图

这其实是Stokes第一问题，通常作为求Navier－Stokes方程解析解的范例[8]。这里采用近似的反解法来给出问题的定性解答。根据边界处流体的流动特征，假设在速度扰动传播距离内，即≤，速度场沿方向的分布呈二次函数的形式，与速度梯度相对应的粘性力则呈线性分布；在速度场扰动传播范围的前端，即＝处，速度为自由流速0，粘性力为零；在＝0处，流体速度为零。因此可确定速度函数有以下形式：

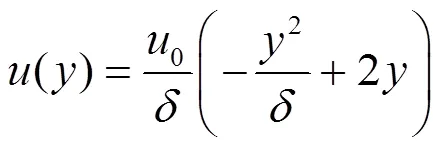
式（1）中速度扰动传播距离为待定参数，可以通过流体运动所遵循的动量定理求得。为此，在任一时刻，取高度范围为该时刻速度扰动传播范围、底面为单位面积流固界面的柱状流体单元来分析，其动量的大小为：

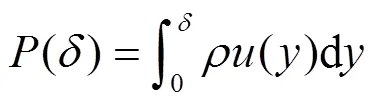
根据动量定理，有：

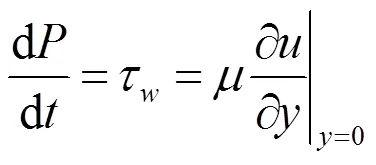
式中：、分别为流体密度和动力粘度；τ为流体单元所受到的单位面积板面的摩阻力。

结合式（1）～式（3），得：

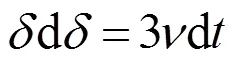
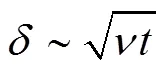
这与精确解中所描述的定性规律一致。

2 平板层流速度边界层的直观模型

有了无限长平板板面处速度扰动在半空间流体中的一维传播定性规律后，进一步构建平板层流边界层的直观模型。为此，将前面的无限长平板换成半无限长平板。半无限长平板板面与半空间流体的右半边界接触，两者以速度0在平板自身平面内沿轴方向运动。在＝0时刻，板突然静止不动，由于粘性，界面处的流体流动会受到阻滞，从而引起流体速度场的扰动，该扰动将沿着方向传播。下面分析半无限长平板对流体速度场的扰动情况，如图2所示。

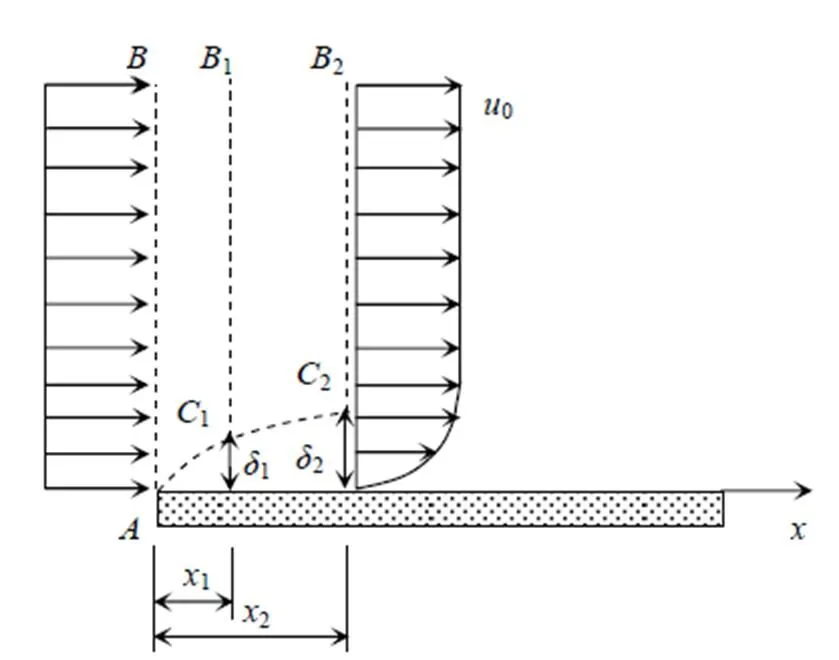
图2 半无限长平板边界区域流速分布示意图

在＝0时刻，取板前端处垂直于轴的流体面为研究对象，流体面以初速度0进入平板区域，并受到板面边界的影响，使得流体面点处流体质点的速度变为零。

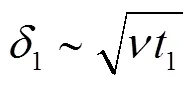
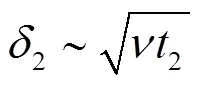
如此继续下去。

通过以上分析可知，对进入平板区域的各流体平面，其上速度场扰动传播的边界由曲线12¼构成，该曲线的参数方程为：

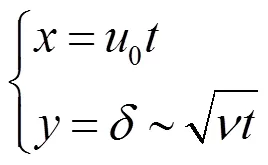
从式（5）式消去，可得自入口端边界层厚度的定性演化规律为：

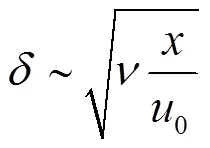
或者：

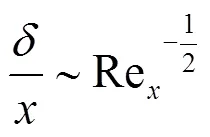
这里，通过一个流体面运动学的直观讨论，给出了平板层流速度边界层的形成和边界层厚度演化的定性规律。

当然，这一直观模型是初等的、近似的，它没有精确考虑质量和动量的守恒条件。可通过进一步引入边界层位移厚度和边界层动量厚度来进行补充说明。

另外，从直观模型中还可以概括出平板层流速度边界层形成的两个条件为：

（1）物理条件：流体粘性，使得边界对流速产生扰动，并使速度扰动沿边界法向传播；

（2）几何条件：边界前端的存在，使得在有限入口段，边界对来流速度扰动的法向传播被限制在有限时间/0内，从而其传播距离被限制在()范围内。

理论上，假设没有边界前端，这将成为有着无限长边界的Stokes第一问题，在该问题中，无限长板面对流速的扰动将沿板面法向无限传播下去，因而形成不了边界层。实际中，所有的边界都是有限的，存在有限远的边界前端。

3 结论

本文在半空间流体无限长边界处速度扰动的一维传播定性规律基础上，建立了平板层流边界层的直观模型，通过运动学角度的讨论，给出平板层流边界层形成的原因、条件，以及边界层厚度演化过程的直观描述和定性规律。

[1]Schlichting H. Boundary Layer Theory[M]. New York：McGraw- Hill，1960.

[2]陈晗，任鹏，任永泉. 离心式风机边界层流场计算[J]. 石油化工设备，2008，37（5）：51-52.

[3]吴文平，张晓宏，田嘉宁，李建中. 考虑重力及离心力的溢流坝反弧段紊流边界层动量积分方程的数值计算[J]. 水动力学研究与进展（A辑），2007，22（1）：9-16.

[4]李建明，谭波，陈文梅. 流动结构对陶瓷管膜滤器过滤性能的影响[J]. 机械，2000，27（3）：14-18.

[5]张晓露，武卫，周章文，杨卓君. 螺旋槽管内传热及阻力特性的数值研究[J]. 机械，2014，41（2）：23-26.

[6]马雷. 边界层理论在低比转速离心泵叶片设计中的应用[D]. 兰州：兰州理工大学，2005.

[7]韩红彪，高善群，李济顺，张永振. 基于边界层理论的盘形转子流体阻力研究[J]. 机械科学与技术，2015，34（10）：1621-1625.

[8]Batchelor G. K. An introduction to fluid dynamics [M]. New York：Cambridge University Press，1967.

[8]陈辉，黄巧亮. 基于矢量控制的BLDCM新型滑模控制器[J].机电工程，2017，29（06）：79-82.

An Intuitive Model for Laminar Boundary Layer

SUN Zehui

( School of Electrical Engineering and Automation, Anhui University, Hefei 230601, China)

The concept of boundary layer is very important in fluid mechanics. In this paper, we first presented a qualitative solution of one-dimensional propagation of the velocity perturbation introduced at the infinite boundary of half-space fluid by an approximation method. Based on this qualitative solution, an intuitive model of the laminar boundary layer on a flat plate was introduced. In this intuitive model, the formation of the laminar boundary layer and its thickness evolution can be depicted by a simple geometric description of the kinematics of a fluid surface, and the physical and geometric conditions of the formation of the laminar boundary layer is also evident.

boundary layer；intuitive model；kinematic analysis

O35

A

10.3969/j.issn.1006-0316.2018.05.005

1006－0316 (2018) 05－0019－03

2017－10－26

孙泽辉（1979－），男，安徽合肥人，博士，讲师，主要研究方向为计算力学与计算传热学。