基于BLUE的双站纯方位跟踪算法*

盛 琥，赵温波

(1 中国电子科技集团第38研究所，合肥 230031； 2 陆军炮兵防空兵学院，合肥 230037)

0 引言

随着多站同步问题的解决，多站无源定位与跟踪技术成为研究热点。纯方位定位系统由于不辐射信号，隐蔽性较好，受到学者关注。受站点布局和非线性等因素影响，多站纯方位系统定位精度不高，需要研究非线性滤波技术提高精度。现有的非线性滤波技术主要有扩展卡尔曼滤波(EKF)[1]、确定采样型滤波(UKF、CKF)[2-3]、随机采样型滤波(PF)[4]和量测转换等[5-7]。EKF方法简单高效，但估计误差较大。确定采样方法能逼近估计误差的二阶项或更高，但计算量比EKF高一个量级。PF对非线性非高斯问题有很强的解决能力，但计算复杂度高，其实用还需时日。量测转换将非线性量测转换到直角坐标系中，估计转换误差统计特性后，再用标准卡尔曼滤波器跟踪，其估计精度较高，且计算量不大，自提出以来得到一些应用。量测转换方法分为三类：嵌套量测转换[8]，基于观测的量测转换[9]和线性最佳无偏估计[10-11](BLUE：Best Linear Unbiased Estimation)。BLUE滤波器在动态模型与目标运动模式匹配时，能实现最优估计。文中将以双站纯方位定位系统为对象，建立目标观测模型，分析量测转换误差统计特性，推导对应的BLUE滤波器。

1 双站纯方位系统的BLUE滤波模型

BLUE算法可以解决量测非线性问题(如雷达目标跟踪)。算法假设目标状态满足关系：

xk=Fk/k-1xk-1+wk

(1)

式中：xk是k时刻目标状态；观测噪声为wk～N(0,Qk)；Fk/k-1是状态转移矩阵。

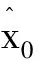
(2)

第二步估计预测误差统计特性。

(3)

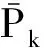
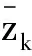
(4)

第四步计算k时刻滤波增益因子Kk。

(5)

第五步状态估计。

(6)

第六步计算估计误差的协方差阵。

(7)

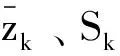
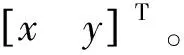
(8)

(9)

式(9)在真实值附近展开后保留二阶项，有转换量测zk的表达式为：

(10)

其中：

分析式(10)发现，将方位量测转换到直角坐标系后，其量测转换误差不再是无偏的，而是表现出有偏性，如式(11)所示:

(11)

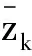
(12)

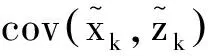
[P(:,1)P(:,3)]

(13)

(14)

Sk中S11参数定义如下：

(15)

(16)

类似可推导出Sk中其它参数值。

(17)

(18)

2 仿真

为验证文中算法性能，将其与两种主流的非线性滤波方法——EKF和UKF比较。仿真场景如下：以测向站之间中点为坐标原点，两测向站坐标分别为(-15 km,0)、(15 km,0)，测向精度3°。目标从(-20 km,24 km)出发，以(200 m/s,0)速度匀速运动，沿各轴加速度摄动0.01 m/s2。目标起始位置误差10 m，速度误差10 m/s，初始滤波协方差阵102I。采样周期1 s，仿真时长200 s，用UKF、EKF和BLUE分别跟踪，仿真次数500次，仿真结果如图2～图5所示。

由图2～图5可见，BLUE滤波器和UKF的跟踪性能相同，EKF的跟踪性能稍差；在滤波置信度比较上，BLUE和UKF都接近1，而EKF略大于1，即有轻微的滤波失配。究其原因，因为BLUE和UKF能够逼近估计误差的高阶项(如式(14)～式(18)所示)，而EKF只对预测状态做一阶近似，因此性能略差。

仿真二中，其它条件不变，将各轴摄动加速度增至3 m/s2，仿真结果如图6～图9所示。

图6～图9中，由于过程噪声显著增大，EKF对误差高阶矩估计不足的弱点被掩盖，三种算法的跟踪精度和置信度相近。为全面评估性能，对算法计算效率做了比较，表1是跟踪场景中各算法的运行时间。

表1 算法运行时间对比 s

综合仿真结果，有以下结论：EKF计算负荷最小，但精度稍差，UKF跟踪精度较高，但计算量大。BLUE滤波器在计算量、跟踪精度和滤波置信度上的综合表现较好。

3 结语

量测转换在雷达中广泛使用，但在其它系统中尚未推广。文中研究双站纯方位系统中的BLUE滤波算法，并与经典非线性滤波方法比较。由于能估计出量测转换误差的高阶特性，算法在不同误差尺度下的性能较好，是一种稳健高效的方法。另外发现：所提BLUE滤波器在目标相对基站的布局变差时，跟踪性能会恶化甚至发散，下一步将针对该问题开展研究。