有限交换环上的Chowla定理

马 宁， 彭国华

(四川大学 数学学院, 四川 成都 610064)

1948年,Vijayaraghavan等[1]证明了一个关于整数环上的完全剩余系的定理：设整数q>2，r1,r2,…,rn和s1,s2,…,sn分别是模q的两组完全剩余系，则r1s1,r2s2,…,rnsn不是模q的完全剩余系．1954年，Coles等[2]利用数学归纳法又给出这一定理的一个简单证明．1987年，孙琦等[3]将这一定理推广到了Dedekind整环中．本文将Chowla定理推广到一般有限含幺交换环．为此，定义了M-环，还讨论了这类有限交换环的基本性质及判定的充要条件．

设R={r0,r1,…,rn-1}是一个有限含幺交换环，始终假定r0=0，相应地r1,r2,…,rn-1是R中的全体非零元素．若s0,s1,…,sn-1是r0,r2,…,rn-1的任意一个排列且s0≠0, 则存在k≥1使得sk=0.此时r0s0=rksk=0，集合S={risi|0≤i≤n-1}至多含有n-1个元素，从而S≠R．这表明，只要R不是零环[4]，则总存在r0,r1,…,rn-1的一个排列s0,s1,…,sn-1，使得S≠R．对于集合

S={risi|0≤i≤n-1}，

是否总有S≠R成立？

定义一个有限含幺交换环R为M-环，如果对于R中全体元素的任意一个排列s0,s1,…,sn-1，总有

{risi|0≤i≤n-1}≠R．

假设s0=0且R=Fq是q元有限域，q为一个素数的方幂，那么环R的乘法群

注意到方程Xq-1-1=0的解集为R×，有

所以q必为偶数．

若q为2的方幂，即R=F2m，m是正整数，则Frobenius映射σ(x)=x2是R上的自同构．取si=ri，i=0,1,…,q-1，则有

这表明R不是M-环．

定理1有限域是M-环的充要条件是它的特征为奇数．

设R=R1⊕R2⊕…⊕Rm是有限含幺交换环R的一个直和分解．对0≤i≤n-1，可以令

ri=(ri1,ri2,…,rim)，si=(si1,si2,…,sim)，

其中,rij,sij∈Rj，1≤j≤m．所以S=R当且仅当

Sj={rijsij|0≤i≤n-1}=Rj

对每个1≤j≤m均成立．于是，有

定理2设R为有限含幺交换环，则R是M-环的充要条件是其直和因子中至少有一个是M-环．

如下的结构性质保障了可以将一般的有限交换环分解成一些小的环的直和．

引理1任意有限含幺交换环可分解为有限交换局部环的直和．

Pi∩Pj=PiPj．

另一方面，R的幂零根

所以R的Jacobson根

但Nil(R)中的每个元素均为幂零元，J(R)是幂零理想．因此存在正整数t使得

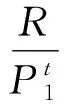
根据定理2和引理1，只需要讨论有限局部交换环何时是M-环．

引理2若一个有限局部交换环不是域，则它是M-环．

证明设R={r1,r2,…,rn}是有限局部交换环．若R不是M-环，则存在r1,r2,…,rn的一个排列s1,s2,…,sn使得

S={risi|0≤i≤n}=R．

设P是R的唯一极大理想且|P|=k，则R恰有k个不可逆元，且Jacobson根J(R)=P为幂零理想．因此存在正整数n0使得Pn0=(0)．不失一般性，可设

r1,r2,…,rk∈P, rk+1,rk+2,…,rn∈R×,

则必有s1,s2,…,sk∈P且sk+1,sk+2,…,sn∈R×．否则，若存在j0>k，sj0∈P，则有

r1s1,r2s2,…,rksk,rj0sj0∈P

且这些元素两两不同.这与R恰有k个不可逆元的假设矛盾．于是

P={r1s1,…,rksk}⊆P2，

从而P=P2，故P=Pn0=(0)．这表明零理想是极大理想，R必为域，与假设矛盾．

定理3设R为有限含幺交换环，则R是M-环的充要条件是R不能分解为特征为2的有限域的直和．

证明由引理1，R=R1⊕R2⊕…⊕Rm，其中Ri(1≤i≤m)是有限交换局部环．若R不能被分解为特征为2的有限域的直和，则存在1≤i0≤m，使得Ri0不是域或者Ri0是奇特征的有限域．根据定理1和引理2，Ri0是M-环．再由定理2可知，R是M-环．

反之，若R是特征为2的有限域的直和，则由定理1和定理2可知，R不是M-环．

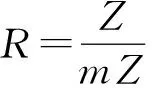
下面考虑定理3在置换多项式方面的应用．环R上的多项式f(X)∈R[X]称为R的置换多项式，如果对应的多项式函数f:R→R诱导出R中元素的一个置换．有关有限交换环上的置换多项式及其应用的讨论，可参考文献[5-10]．因为一个置换多项式可以产生环中元素的一个置换，所以立即得到以下推论.

推论1M-环上的两个置换多项式的乘积不再是置换多项式．

[1] VIJAYARAGHAVAN T, CHOWLA S. On complete residue sets[J]. Q J Math,1948,19(1)：193-199.

[2] COLES W, OLSON F. A note on complete residue systems[J]. Am Math Monthly,1954,61(9)：662-622.

[3] 孙琦，旷京华. 关于代数数域中的完全剩余系[J]. 数学学报,1987,30(2)：226-228.

[4] ATIYAH M, MACDONALD I. Introduction to commutative algebra[M]. New Jersey:Addison-Wesley,1969.

[5] BINI G, FLAMINI F. Finite commutative rings and their applications[M]. New York: Spring Science and Business Media,LLC,2002.

[6] 孙琦,万大庆. 置换多项式及其应用[M]. 沈阳:辽宁教育出版社,1987.

[7] LIDL R, NIEDERREITER H. Finite Fields[M]. Encyclopedia Math Appl 20.Cambridge:Cambridge Univ Press,1997.

[8] COHEN S D. Permutation Group Theory and Permution Polynomials in Algebras and Combintorics[M]. Hong Kong:Springer-Verlag,1997.

[9] FRISCH S. Polynomial functions on finite commutative rings[M]. Lecture Notes in Pure and Appl Mathematics 205.New York:Dekker,1999.

[10] ZHANG Q. Polynomial functions and permutation polynomials over some finite commutative rings[J]. J Number Theory,2004,105(1):192-202.