基于阵列声波测井评价致密砂岩储层地应力
孙杰文, 尹帅, 崔明月, 吴志均
(1.中国石油勘探开发研究院廊坊分院, 河北 廊坊 065007;2.西安石油大学地球科学与工程学院, 陕西 西安 710065)
0 引 言
煤系致密砂岩储层具有强非均质性及各项异性,其有效开发多采用水力压裂改造及水平井开发方式[1]。现今地应力属性可以为压裂设计及水平井井网优化提供依据[2]。测井具有高分辨率特征,利用测井资料进行现今地应力评价是一种有效的方法。目前世界范围内主要的现今地应力测井评价模型大体包括莫尔-库伦准则模型、单轴应变模型及地层各项异性模型3类[3]。对于强非均质性煤系地层而言,地层各项异性模型较为适用。鄂尔多斯盆地东北缘上古生界发育多套煤系致密砂岩气储层,含气层系多。对于同一套气层,储层改造的效果差异大,致密砂岩储层可改造性尚未开展相关研究[4]。因此,对该地区上古生界气藏储层进行现今地应力测井评价,可以为制定合理的煤系致密砂岩气储层开发方案提供参考。本文以鄂尔多斯盆地东缘A区气藏为例,建立了基于阵列声波测井且适用于研究区上古生界煤系致密砂岩气藏的现今地应力测井评价方法。研究成果可以为盆地内类似地区提供参考。
1 阵列声波测井
研究区位于鄂尔多斯盆地东缘A区,其构造位置位于鄂尔多斯盆地伊陕斜坡和晋西挠摺带上,地势呈东高西低、北高南低[4]。该地区上古生界发育多套煤系致密砂岩气储层,含气层系多,包括石千峰组5段、盒1段、盒2段、盒3段、盒4段、盒5段、盒6段、盒7段、盒8段、山西组及太原组。采用全波列阵列声波测井仪器对上古生界目的层进行了声波测试,仪器包含声波采集系统、声波接收阵列、单级发射器及偶极子发射器。主要优点:①可以探测全波列信息,具有高信噪比,横波波速测试结果质量高;②克服了在软泥岩或煤岩中其他测井无法获取横波波速的不足;③可以测得快横波信息,从而可以对地层各向异性及含气性进行评价。
2 岩石力学参数评价
2.1 纵横波时差关系
全波列阵列声波测井可以获取地层可靠的横波时差信息,当区分砂泥岩时,不同地层的纵横波时差之间具有非常好的正相关性。下石盒子地层纵横波时差之间的关系见图1。

图1 下石盒子组地层纵横波时差拟合关系*非法定计量单位,1 ft=12 in=0.304 8 m,下同
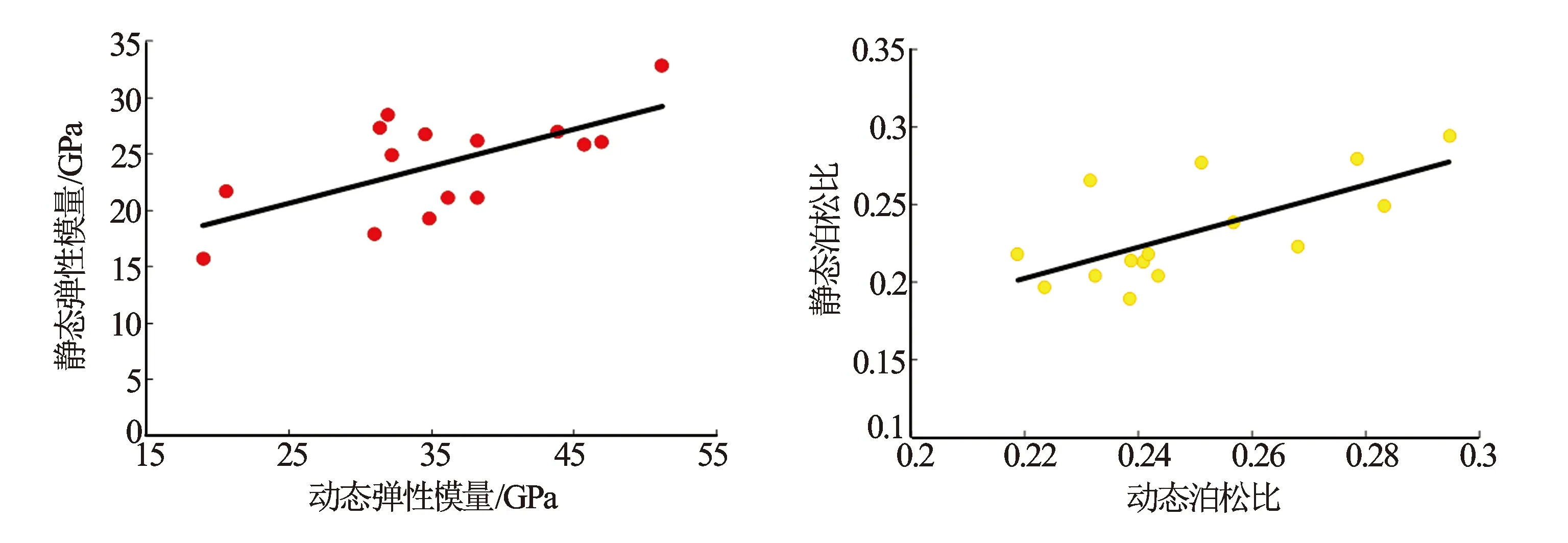
图2 致密砂岩岩样的动静态弹性参数转换关系
2.2 动静态岩石力学参数转换关系
动静态岩石力学参数实验仪器采用MTS岩石物理测试系统。实验测试的样品共计15组,取自石千峰组、上石盒子组及太原组层位。
分别采用物理方程[见式(1)、式(2)]计算岩石的弹性模量及泊松比。岩石的动静态弹性参数间存在差异,通常岩石动态弹性参数值要略大于其静态值,静态力学参数适用于工程及地质评价[5]。最终建立研究区上古生界致密砂岩岩样的动静态弹性参数转换关系(见图2)。
(1)
(2)
式中,Ed为动态弹性模量,GPa;Δtp为纵波时差,μs/ft;Δts为横波时差,μs/ft;ρb为岩石密度,g/cm3。
3 压裂法地应力评价
沉积盆地中,岩石受骨架应力(σ)和地层压力(pp)的共同影响,这两者的合力即为有效应力(σ′)。对于中等及强固结岩石,考虑到颗粒支撑岩石内部存在较强的压实及胶结作用[6],孔隙流体实际上未完全承担全部地层压力。因此,Biot提出了有效应力理论[7]。研究区上古生界煤系致密砂岩具有强压实特征,β(有效应力系数)值与孔隙度(φ)关系密切,可采用式(3)对β进行定量表征[7]。研究区上古生界气藏基本处于常压状态,压力系数为1。
β=1-(1-φ)3.8
(3)
小型水力压裂测试可以准确获取所压裂地层的现今地应力。完整的压裂过程中,压裂曲线清晰地记录了地层的压力变化等信息[8]。水平最小主应力(σh)即为裂缝闭合压力(pc)。当确定了pc之后,可以根据式(4)[9]求取地层水平方向最大主应力(σH)
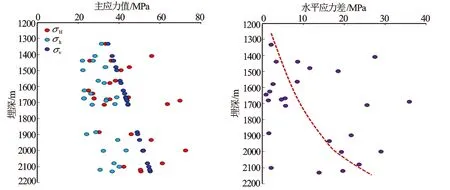
图3 各主应力分布与埋深的关系
(4)
式中,σH为水平方向最大主应力,MPa;pc为裂缝闭合压力,MPa;pf为破裂压力,MPa;pp为地层压力,MPa;T为岩石抗张强度,MPa。
利用上述方法计算获得了研究区上古生界致密砂岩气藏储层的现今地应力。随着埋深的增加,3个方向主应力均有逐渐增加的趋势,整体来看,地应力状态基本满足σh<σH<σv。部分数据呈现出σh<σv<σH的应力状态,表明局部地层应力环境复杂,具有较强的构造应力值(见图3)。随着埋深的增加,水平差应力(σH-σh)也具有逐渐增加的趋势。
4 现今地应力测井评价
4.1 测井解释方案
现今地应力解释模型主要包括莫尔-库仑破坏模式、单轴应变模式及各向异性地层模式[10]。莫尔-库仑破坏模式虽然具有一定的物理基础,但其假设地层最大原地剪应力是由地层的抗剪强度决定的,该模式比较适合松软的泥页岩地层,不具备普遍的意义。单轴应变模式假设沉积地层只发生垂向应变,水平方向应力完全由垂向应力诱导而产生,因此,水平方向各个主应力均相等。该类模式通常只适用于弱构造运动地层,如盆地腹部地层[11]。各向异性地层模式较好地考虑了水平方向地应力的非均一性。主要不足为待定系数较多,计算过程繁琐。
为简化计算过程,同时提高预测精度。通过不同计算模型对比,发现引入修正系数C*至Newberry模型中,可以较好地预测地层水平方向最小主应力[见式(5)][12]。对于水平最大主应力,考虑到地层应力的各向异性,引入非平衡结构因子(Ub),σH的表达式见式(6)[13]。
(5)
σH=σh×Ub
(6)
Ub可以利用双井径资料获取
(7)
式中,Dmax为井眼直径最大值,cm;Dmin为井眼直径最小值,cm;E为岩石弹性模量,GPa;Ema为岩石骨架弹性模量,GPa;k为刻度系数。
垂直主应力由上覆地层的重力梯度决定,可通过密度测井曲线进行积分获得

(8)
式中,H为地层埋深;ρ(z)为埋深z处的地层岩石密度。

图5 A-2井地应力测井解释成果图
4.2 测井评价结果
研究区志留系取心岩样地应力测试结果与解释结果间对比见图4。预测结果的符合度较高,从预测误差上看,σH的绝对误差分布在0.75~10.49 MPa,平均绝对误差为5.91 MPa;σh的绝对误差分布在0.42~6.82 MPa,平均绝对误差为3.13 MPa。整体来看,该测井解释方案的精度较高,能够满足工程需要。

图4 现今地应力测井解释结果与实测值对比图
利用上述方法建立了单井地应力测井解释剖面(见图5)。可以看出,随着埋深的增加,各主应力均有逐渐增加的趋势。3个方向主应力间满足σh<σH<σv,与前述地应力测试结果基本一致。部分层段呈现出较高的σH值,表现为其值与σv值较为接近,代表局部地层具有较强的构造应力环境[11]。
同时,本文基于阵列声波测井对目的层进行了快横波分析,确定了现今地应力方向。在σH方向,岩石的压实程度最高,横波的传播速度最快[13]。从分析结果看,该套上古生界地层所受的应力挤压方向基本一致,为NW向,表明其受同一套应力系统的影响。但对于煤系地层而言,不同层系(又称“地质力学层”)的岩石力学性质及构造特征等方面因素均具有较强的差异,因而地应力在纵向上表现出较强的差异性。
研究建立了一套基于全波列阵列声波测井的现今地应力测井解释方法,该方法适用于鄂尔多斯盆地东缘上古生界煤系致密砂岩气藏。解释结果可以为该地区致密砂岩气藏储层高效开发提供参考和依据(见图6)。

图6 A-10井阵列声波各向异性分析成果图
5 结 论
(1) 获得研究区目地层的动静态力学参数转换关系,利用压裂法计算了地层地应力,其状态满足σh<σH<σv,局部地质力学层呈现出较高的构造应力环境。
(2) 引入修正系数C*至Newberry模型中,实现了对煤系致密砂岩储层水平方向最小主应力的预测。同时,考虑到地应力的各向异性,引入非平衡结构因子Ub,对储层水平最大主应力进行了测井评价。
(3) 快横波方位分析结果表明,研究区上古生界气藏的水平最大主应力方向为NW向。
参考文献:
[1] NELSON E J, MEYER J J, HILLIS R R, et al. Transverse Drilling-induced Tensile Fractures in the West Tuna Area, Gippsland Basin, Australia: Implications for the In-situ Stress Regime [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42: 361-371.
[2] HODA D, MORTEZA N T, AMIN S, AFSHIN T. Geo-mechanical Modeling and Selection of Suitable Layer for Hydraulic Fracturing Operation In An Oil Reservoir (South West of Iran) [J]. Journal of African Earth Sciences, 2015, 111: 409-420.
[3] KARACAN C Ö. Elastic and Shear Moduli of Coal Measure Rocks Derived from Basic Well Logs Using Fractal Statistics and Radial Basis Functions [J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 1281-1295.
[4] 傅宁, 杨树春, 贺清, 等. 鄂尔多斯盆地东缘临兴-神府区块致密砂岩气高效成藏条件 [J]. 石油学报, 2016, 37(增刊1): 111-120.
[5] HOU H J, WANG W H, ZHU X M. Study of Depositional Model of Silurian System in Tazhong Area, Tarim Basin [J]. Acta Sedimentologica Sinica, 1997, 15(3): 41-47.
[6] BIOT M A. General Theory of Three Dimensional Consolidation [J]. Journal of Apply Physics, 1941, 12(2): 155-164.
[7] WU B. Biot’s Effective Stress Coefficient Evaluation: Static and Dynamic Approaches [C]∥ISRM-2nd Asian Rock Mechanics Symposium, Beijing, 2001: 11-13.
[8] 孟文, 陈群策, 吴满路, 等. 龙门山断裂带现今构造应力场特征及分段性研究 [J]. 地球物理学进展, 2013, 28(3): 1150-1160.
[9] KANG H, ZHANG X, SI L, et al. In-situ Stress Measurements and Stress Distribution Characteristics in Underground Coal Mines in China [J]. Engineering Geology, 2010, 116: 333-345.
[10] ZOBACK M D, BARTON C A, BRUDY M, et al. Determination of Stress Oritation and Magnitude in Deep Wells [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40: 1049-1076.
[11] 申瑞臣, 屈平, 杨恒林. 煤层井壁稳定技术研究进展与发展趋势 [J]. 石油钻探技术, 2010, 38(3): 1-6.
[12] DENG J, ZHU W Y, MA Q . A New Seepage Model for Shale Gas Reservoir and Productivity Analysis of Fractured Well [J]. Fuel, 2014, 124: 232-240.
[13] LIU CHAORU. Distribution Laws of In-situ Stress in Deep Underground Coal Mines [J]. Procedia Engineering, 2011, 26: 909-917.

