一种提高步进电动机细分精度的设计方法

李 雨，谭金玺，宁剑建，吕 强，宋振民，朱志强

(1.中国电子科技集团公司第二十一研究所，上海 200233；2.宁波中大力德智能传动股份有限公司，宁波 315000)

一种提高步进电动机细分精度的设计方法

李 雨1，谭金玺2，宁剑建1，吕 强1，宋振民1，朱志强1

(1.中国电子科技集团公司第二十一研究所，上海 200233；2.宁波中大力德智能传动股份有限公司，宁波 315000)

摘 要：介绍了一种提高混合式步进电动机步距角细分精度的设计方法，并进行了样机试制。样机测试结果表明,采用该设计方法，步进电动机细分后步距角均匀，满足某型号卫星的成像精度要求。

关键词：步进电动机；样机试制；细分精度

0 引 言

近年来，混合式步进电动机由于力矩大、可靠性高、控制简单方便、断电后存在自锁力矩等优点[1]，被广泛用于航天器的各种伺服驱动机构，是系统的关键部件，发挥着重要作用。但是，目前某些载荷如光学成像系统对成像质量要求更高，要求作为扫描驱动机构动力源的步进电动机能够提供更小的步距角。因此，从降低系统失效风险的角度出发，趋向于采用步进电动机直接驱动。在没有减速器的情况下，要减小电机步距角，唯有增大电机转子齿数和外径，而航天配套产品对电机质量、体积有严格限制。本文结合工程需求，在不增加电机外径尺寸和转子齿数的情况下，通过控制线性细分电机绕组电流及定转子齿层设计，提高了步进电动机微步距开环控制精度。

1 混合式步进电动机结构

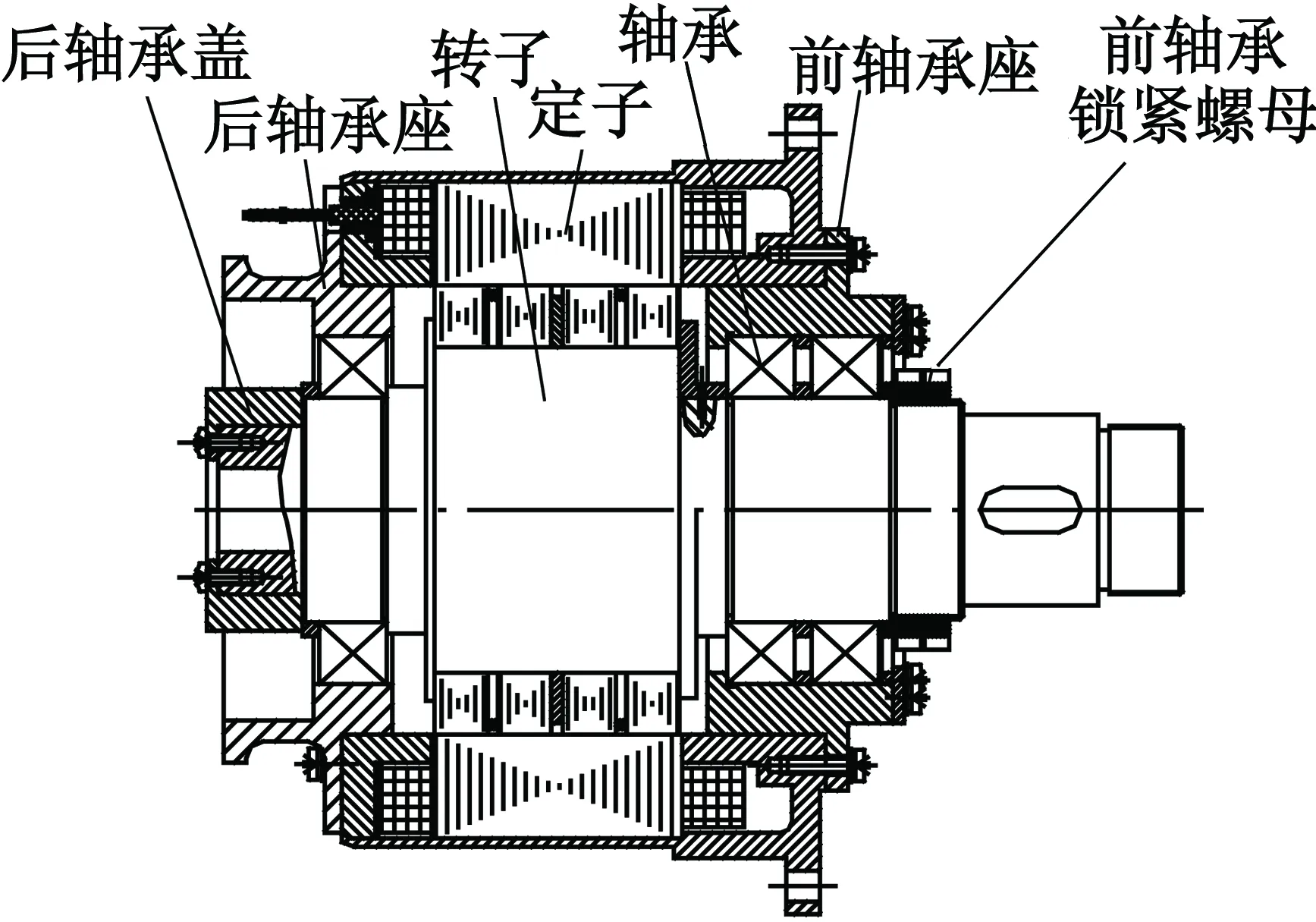
图1 120BH型混合式步进电动机结构

混合式步进电动机结构如图1所示，由定子、转子以及轴承组成。转子上分布4段转子铁心，每段铁心依次错开1/2齿距，其中中间2段转子铁心采用隔磁环隔开。电机轴伸端轴承采用一对角接触轴承，电机出线端采用一套深沟球轴承，既保证了电机旋转精度，又适应了空间环境的高低温交变。

2 步进电动机细分控制

步进电动机细分控制的目的是希望尽量达到等距细分。实际操作时，往往通过将绕组电流等分来实现细分控制，而电流等分却并不能实现等距细分。以该120BH型步进电动机为例，分析说明如下。

该电机转子铁心上均布100齿(zr=100)，电机采用四相单拍工作方式(m=4)，状态转换为A-B-C-D，电机步距角：

(1)

电机采用34细分，A,B两相电流波形如图2所示。

图2 四相34细分A，B相电流波形

如图3所示，经计算可得细分步距角θ1对应的

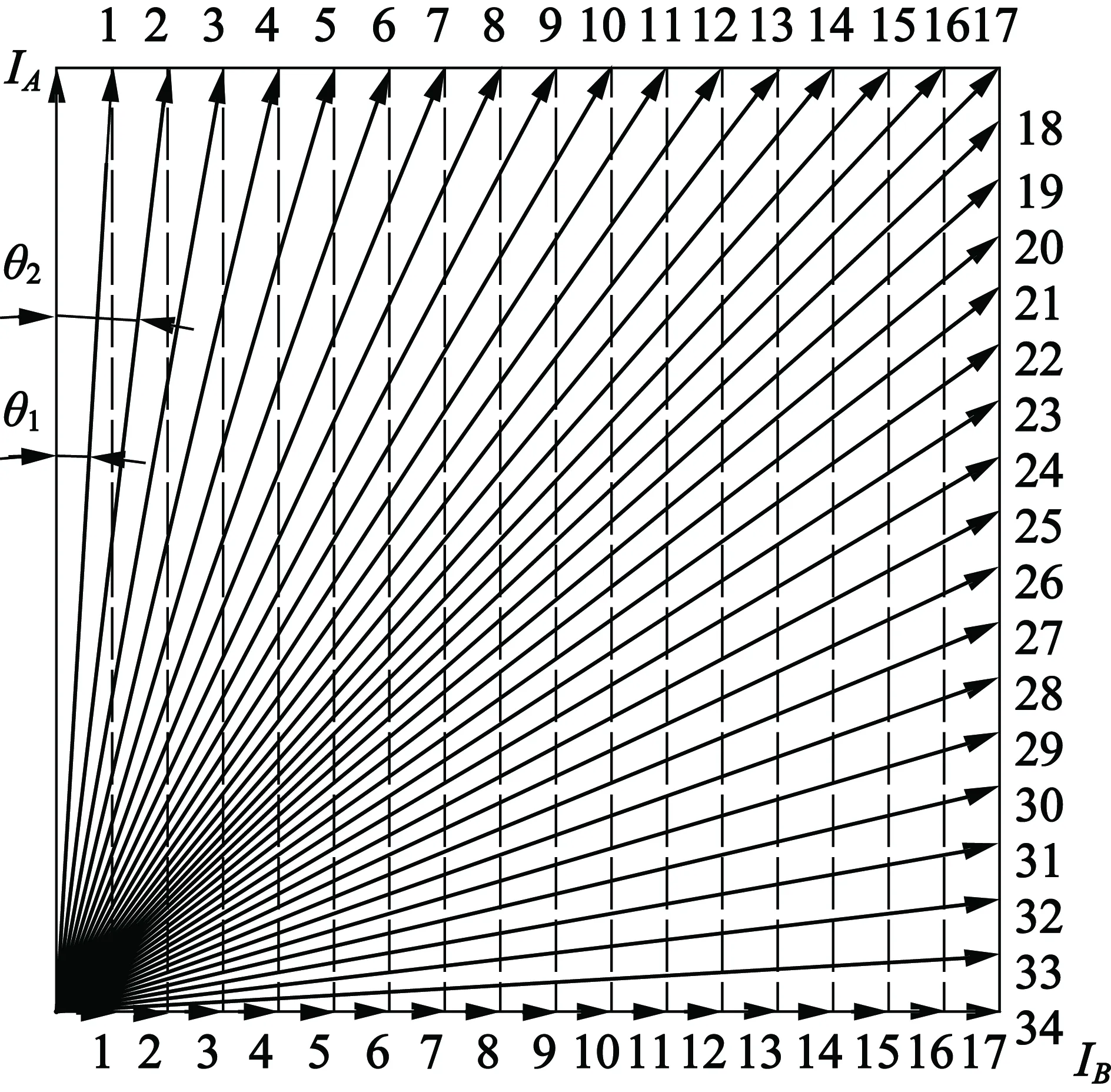
图3 四相34细分时(A→B)合成磁势的旋转情况

机械角度：

同样计算θ2对应的机械角度，可得:

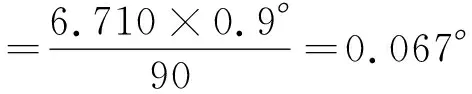
同理，可分别计算得到34细分时理论上的各微步距角度。从上述电机细分合成磁势计算结果可以看到，要达到精确的等距细分，单纯依靠绕组电流等分是很难实现的。而且对于不同电机而言，其控制效果差异较大。理论上要实现等距细分，则需要反算电机通电相各台阶电流，并结合具体样机进行实验，最终形成绕组电流的数据库，驱动控制时再进行查表取值。这种方法的结果是驱动控制复杂，可靠性降低。本文从工程应用和实际需求出发，对步进电动机定转子小齿齿宽进行针对性设计，单纯采用电流等分即可满足工程的控制要求。

3 设计仿真

电机的位置控制归根结底在于对其输出力矩的控制。文献[2]在理论分析的基础上，对混合式步进电动机的电磁转矩公式进行了推导，表达式如下：

式中：p为转子齿数；L2为绕组自感的谐波分量；Msr为定子线圈互感的模[3]。

由于本文仅研究定转子齿宽设计对控制精度的影响，因此为便于仿真计算，简化了电机结构，暂不考虑步进电动机磁钢轴向磁路的影响，建立了仅包含径向磁路的步进电动机模型，从而方便采用ANSYS Maxwell的2D模块进行仿真。通过仿真观察步进电动机在电流等分情况下的稳定平衡位置，对比定、转子等宽与不等宽情况下的区别。

本文仿真计算采用瞬态场，计算模型如图4所示。定、转子铁心材料为H12，计算时忽略铁心损耗。计算稳定平衡位置时，不考虑实际装配条件下轴承摩擦力、负载等其他附加转矩。

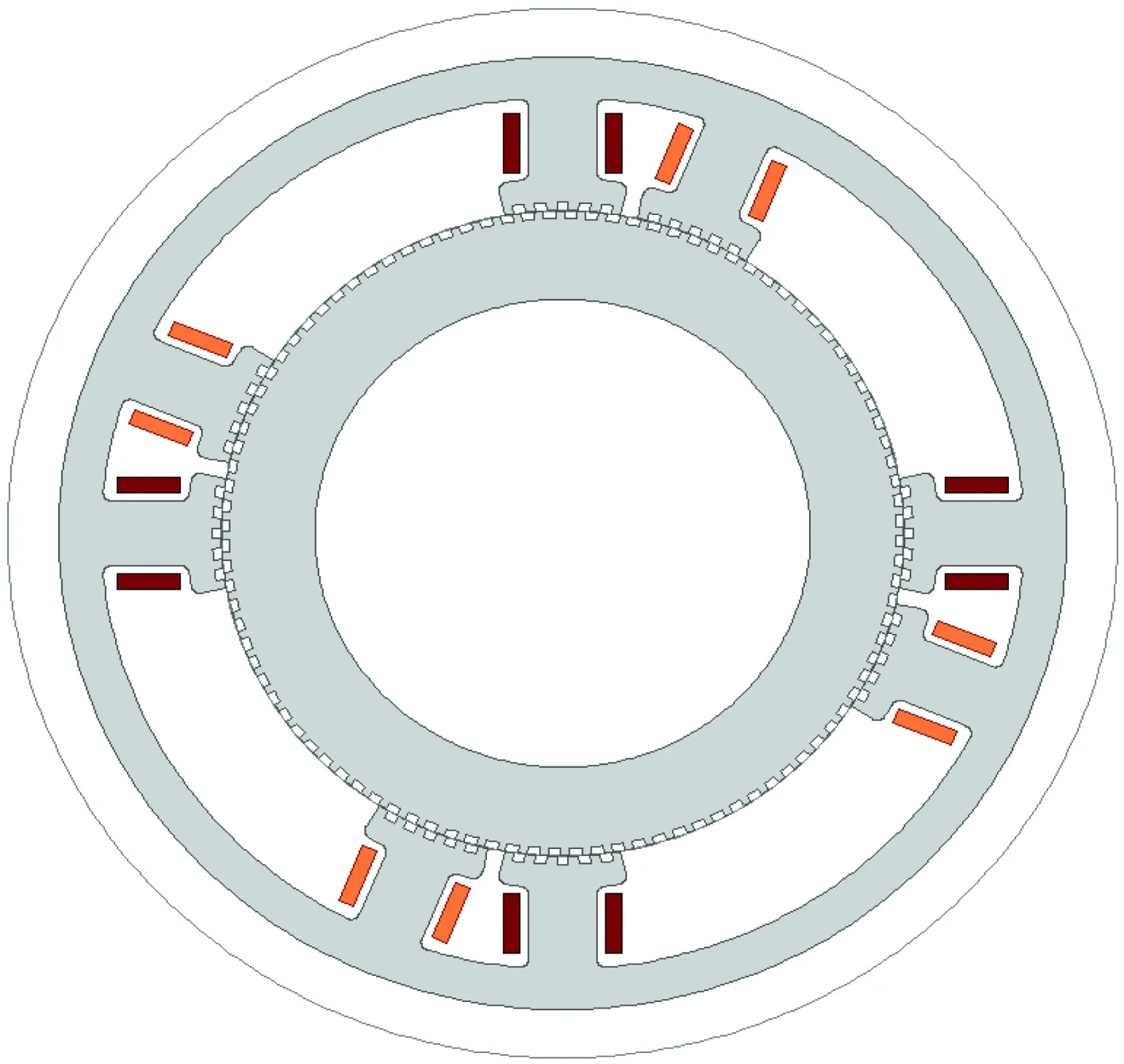
(a) 有限元模型

(b) 网格剖分

模型中A,B两相绕组同时通电时形成的磁场方向如图5所示。

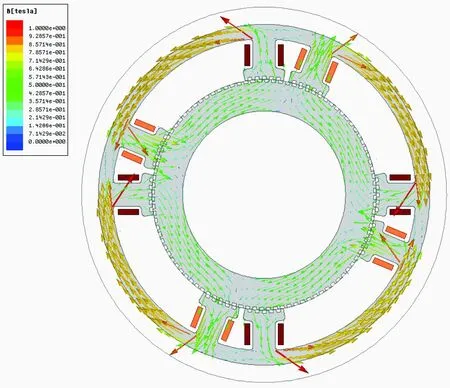
图5 磁场方向

计算时A相电流从2 A开始递减，每次减少0.125 A，B相电流保持2 A不变。比较定、转子等齿宽和不等齿宽的情况可以看到，不等宽的情况下稳定平衡位置变化量较小些，计算结果如图6所示。角度变化量如表1所示。

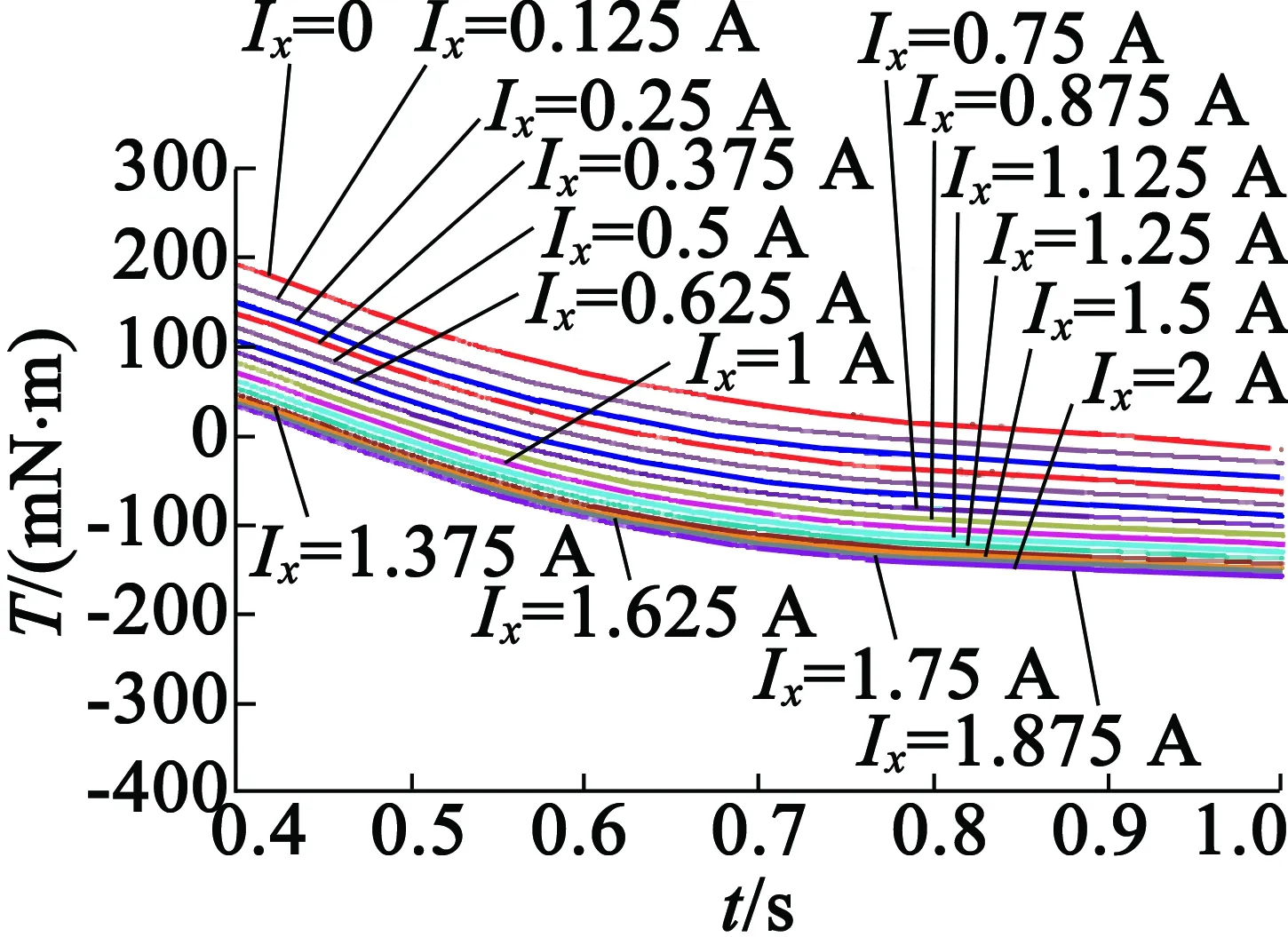
(a) 定、转子齿等宽的

(b) 定、转子齿不等宽的

(c) 线性度仿真结果

对图6的说明如下：

(1) 由于仿真时设置转子转速1°/s，因此横坐标时间轴对应数值即为机械角度(例如0.3 s即对应0.3°)。

(2) 纵坐标为转矩，因此纵坐标为零时对应的横坐标数值即为稳定平衡位置的角度。

(3) 图6(a)、图6(b)中的Ix为A相减少的电流值，即表示A相电流IA=2-Ix(例如Ix=0.25 A，表示该曲线为A相电流IA=2-0.25=1.75 A，B相电流2 A下的计算结果)。从仿真计算可以看到，A相电流等分后，不管定、转子是否等宽，从2 A到0递减的过程中，稳定平衡位置的变化量总体上呈现逐渐减小的规律。在电流较大时，同等电流变化产生的稳定平衡位置变化较大。

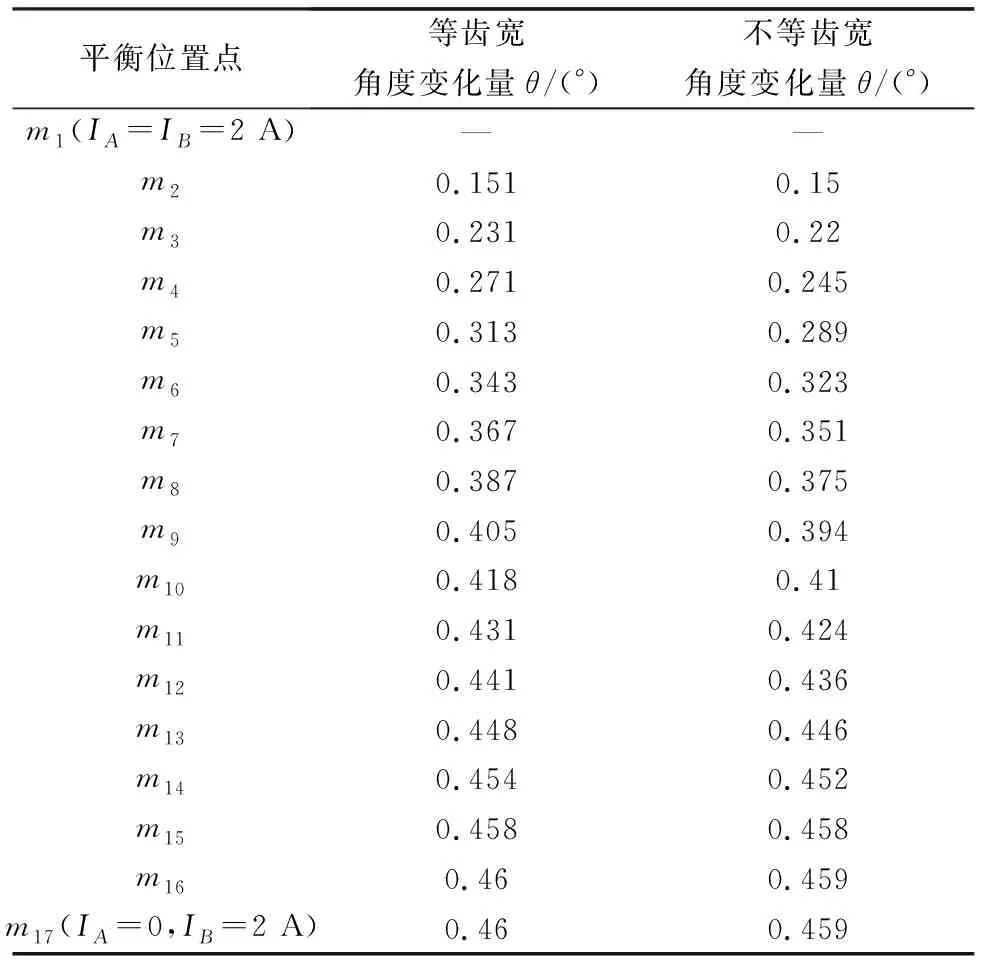
表1 角度变化量

4 样机实例

根据上述分析，研制2台样机。为便于比较分析，2台电机的结构参数除定子小齿宽度不同以外，其余结构参数均相同，具体参数如表2所示。

表2 样机齿层参数对比表

电机整步步距角为0.9°，按照上述电流等分对2台样机步距角0.9°进行34等距细分驱动，细分后微步距角为0.9°/34=0.026°，实际测试细分结果如表3所示。

表3 样机步距角(0.9°)细分结果

步距角细分线性测试样机如图7所示，2台样机细分结果对比如图8所示。

图7 样机步距角内细分步线性测试

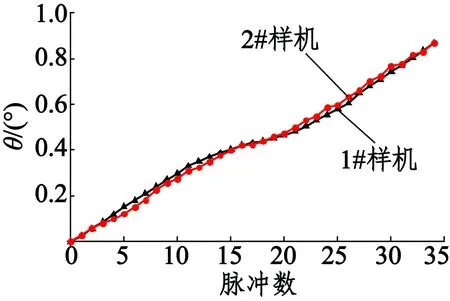
图8 1#样机和2#样机细分结果对比

对比2台样机的细分结果可知，2#样机细分后位置与电流的线性度更好，更有利于保证系统的位置控制精度。

5 结 语

本文通过分析和实验验证，得出步进电动机定、转子小齿齿宽设计对等距细分的影响。步进电动机的开环控制精度不仅由控制方案决定，在很大程度上还取决于电机自身的线性设计。本文通过定转子小齿的齿宽设计，提高了电流线性细分下的步距角细分精度，满足了工程的实际需求。

[1] 刘宝廷,程树康.步进电动机及其驱动控制系统[M].哈尔滨:哈尔滨工业大学出版社，1997.

[2] 王晓丹.基于单片机的步进电机细分驱动系统的研究[D].长沙：中南大学，2008.

[3] 刘鼎邦.两相混合式步进电机细分驱动的研究[D].长沙：长沙理工大学，2012.

ADesignMethodtoImprovetheSubdivdionPrecisionofSteppingMotor

LIYu1,TANJin-Xi2,NINGJian-jian1,LÜQiang1,SONGZhen-ming1,ZHUZhi-qiang1

(1.No. 21 Research Institute of CETC,Shanghai 200233,China;2.Ningbo Zhongda Leader Intelligent Transmission Co.,Ltd.,Ningbo 315000,China)

Abstract:A design method to improve the precision of the stepping angle of the hybrid stepping motor was introduced and a prototype trial system was carried out. The test results of the prototype show that the adopted method, subdivided the rear angle of the stepping motor and it could meet the imaging precision of a certain type of satellite.

Key words：stepping motor; prototype trial; subdivdion precision

中图分类号：TM383.6

A

1004-7018(2018)05-0073-03

2018-01-31

作者简介：李雨(1979—)，男，高级工程师，专业方向为电机及其驱动控制。